基于动态双种群的黏菌和花粉混合算法

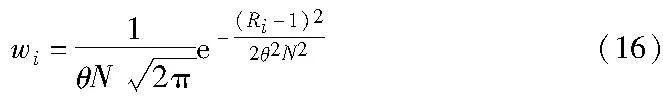
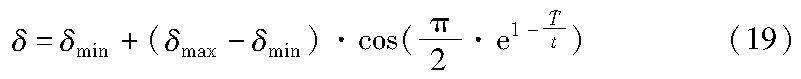
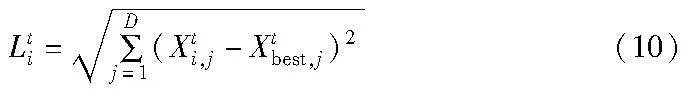
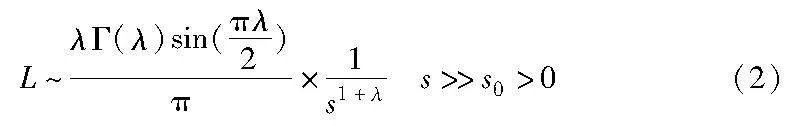
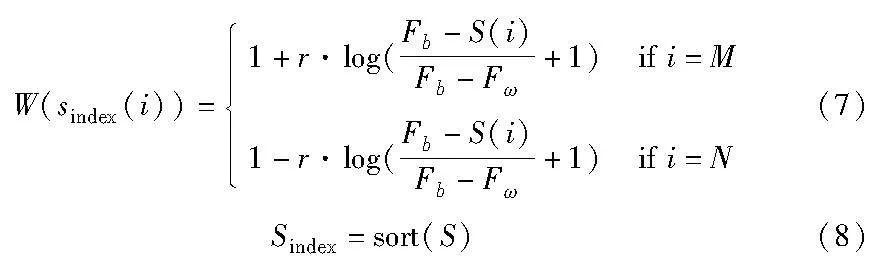
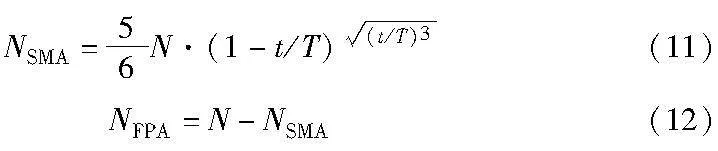
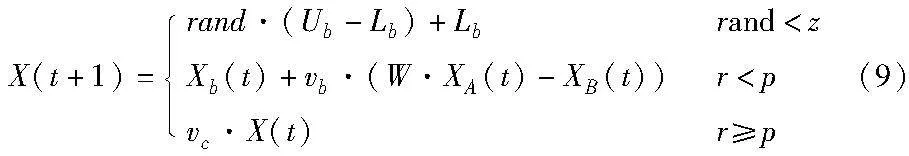
摘 要：针对单一启发式算法易受自身原理导致的全局和局部搜索不平衡的问题，提出了一种基于动态双种群的黏菌和花粉混合算法HASMFP。首先，通过种群个体和当前最优个体之间的距离，将种群动态划分为黏菌子种群和花粉子种群分别进行搜索，以更有效地平衡算法的探索能力和开发能力；其次，对全局搜索融入相似度与适应度的综合排序感知机制来提高黏菌子种群的多样性，以帮助黏菌算法跳出局部最优；最后，在标准花粉算法的全局搜索中加入动态权重和恒定收缩系数，并对局部搜索设计了精英引导项来提高算法的收敛速度和搜索精度。选用CEC2017测试集中的12个函数作为实验测试集，将HASMFP与ISMA、DTSMA、HLFPA、SCFPA和tMFPA五种改进算法进行性能测试对比。还对HASMFP的各个改进策略进行消融实验，实验表明在综合改进策略的共同作用下，HASMFP的优化性能排名第一。基于实验结果的Friedman检验表明，HASMFP能够获取最优的性能。

关键词：混合算法； 黏菌算法； 花粉算法； 动态双种群； 综合排序感知； 精英引导项； 动态权重

中图分类号：TP301.6 文献标志码：A 文章编号：1001-3695（2024）07-019-2052-09

doi：10.19734/j.issn.1001-3695.2023.11.0564

Slime mould and flower pollination hybrid algorithmbased on dynamic dual population

Abstract：Aiming at overcoming drawbacks of imbalance between the global and local search ability of a single heuristic algorithm， this paper proposed a slime mould and flower pollination hybrid algorithm based on dynamic dual population， named HASMFP. Firstly， HASMFP adopted a grouping mechanism that took the distance between individual inside population and the current optimal individual into consideration to dynamically divide whole population into slime mold subpopulation and pollen subpopulation to balance the exploration and development capabilities of the algorithm more effectively. Secondly， HASMFP used a ranking mechanism based on similarity and fitness to improve diversity of slime mold population， and further increased the probability to jump out of local optimal. Finally， HASMFP also adopted a dynamic weights and constant shrin-kage coefficients with an elite guidance terms to further enhance the local and global search ability of standard flower pollination algorithm at the same time. It used 12 test functions from CEC2017 test suit as the testbed to evaluate the performance of HASMFP with other 5 algorithms： ISMA， DTSMA， HLFPA， SCFPA， and tMFPA. It conducted ablation experiments to eva-luate the effectiveness of all improvement strategies applied in HASMFP. Experimental result shows that HASMFP can rank first under the combination of all improvement strategies. The result of Friedman test based on experimental data illustrates that HASMFP can achieve the supreme performance among all evaluated algorithms.

Key words：hybrid algorithm; slime mould algorithm; flower pollination algorithm; dynamic dual population; similarity and fitness ranking; elite guidance term; dynamic weight

0 引言

很多实际的工程优化问题可以转换为求解给定的单目标函数的最优值问题。随着此类工程优化问题的规模和维度越来越大，变量和约束越来越多，使传统数值优化方法难以解决此类问题。受自然界生物的启发，国内外学者已经提出了很多新颖且高效的智能优化算法（也称为启发式算法），如黏菌算法（slime mould algorithm，SMA）［1］、花粉算法（flower pollination algorithm，FPA）［2］等。智能优化算法因其性能高效、易实现的优点被广泛应用于系统调度［3］、无人机路径规划［4］、图像分割［5］等领域，并取得了良好效果。

单一的启发式算法由于自身机制或原理的限制，导致探索与开发之间的不平衡，易出现求解质量较差、陷入局部最优等弊端。目前已有研究［6，7］发现，可以将具有不同优势的两种智能优化算法按照特定规则有机地结合在一起，可以把算法的性能提升到一个新高度。其中，采用high-level与Teamwork相结合的HTH（high-level teamwork hybrid）混合方式［8］是一种常用的将两种不同的智能优化算法进行混合的方法。HTH混合是指将两种不同的算法分别独自运行，各算法的内部运作互不影响，即每个协作算法在各自的解空间中进行寻优，被混合的算法更好地发挥各自的优势，可以使混合算法获得比被混合的算法更优的寻优能力。

目前，对于混合优化算法的研究越来越受重视，已有众多的混合算法被提出并在多个领域得到应用。Abdel-Basset等人［9］提出了一种将差分进化算法（DE）与改进FPA算法相结合的混合算法MFPA。MFPA采用基于概率随机地从多个更新规则选择一个规则的机制对FPA的局部授粉进行改进并融合差分进化算法，从而更好地提高了花粉种群的多样性。Wang等人［10］提出一种基于共生机制的蝴蝶算法（BOA）与FPA算法的混合算法MBFPA。MBFPA采用的共生生物搜索机制在共生阶段具有很强的开发能力并引入了共生相位，有效地提高了算法的寻优能力。MBFPA也利用自适应切换概率来平衡算法的探索与开发。吴文斌等人［11］提出了基于遗传算法（GA）的混合花粉算法HGFPA。HGFPA在算法初期使用混沌序列进行初始化，并在较优位置引入遗传算法的改进交叉和变异策略，实验结果表明HGFPA的收敛速度与精度都得到大幅提升。Chen等人［12］将SMA与算术优化算法（AOA）进行混合得到一种高性能的混合优化算法。该混合算法利用SMA具有较强的全局搜索能力和AOA具有较好的收敛能力的特点获取更好的搜索能力，并被应用于汽车耐撞性设计问题中，结果表明该算法的结合与改进是有效的。Samantaray等人［13］提出了一种基于SMA与粒子群算法（PSO）的混合算法，并使用该算法基于ANFIS模型对洪流进行预测，实验结果表明，混合算法可以在训练中获取最佳的性能。

因为HTH混合方式具有易混合不同算法并能充分发挥被混合算法各自的寻优能力，并且各算法可以在搜索机制上进行互补增强的优点，所以本文基于HTH混合方式提出了一种基于动态双种群的黏菌和花粉混合算法（slime mould and flower pollination hybrid algorithm based on dynamic dual population， HASMFP）。HASMFP主要考虑了需要选择何种算法进行混合。因为混合算法的根本目的是改善算法在探索与开发之间的平衡性，所以需要选择搜索机制能够互补的优化算法。SMA模仿黏菌觅食过程。黏菌在觅食时产生扇形细胞质振荡与收缩特性，形成一个大的静脉网络进行觅食。SMA使用权重系数与其他参数共同影响黏菌振荡收缩的幅度和频率，振荡收缩随迭代的进行逐渐变弱。迭代前期大幅度的振荡收缩行为使SMA具有强大的全局探索能力［14，15］。FPA通过莱维飞行和最优个体的引导进行探索。莱维飞行的特性使花粉大概率处于步长较小的状态［16］，导致算法的探索范围偏小，而当莱维飞行出现大步长时，最优个体的引导作用会对大步长飞行产生阻力，导致FPA更多地偏向局部搜索［17］。从上述分析可以看出，FPA恰好可以弥补SMA迭代后期开发能力较弱的缺陷，所以为了扬长避短，HASMFP选用SMA与FPA构造HTH方式的混合算法。HTH混合方式需要将种群划分为两个独立的子种群，即每个被混合的算法都拥有自己的独立子种群。如果采用固定的子种群，即子种群被划分后保持不变，则容易出现种群多样性差或收敛能力弱等问题，HASMFP利用动态双种群机制来改善上述问题。HASMFP还分别对SMA和FPA进行了改进，以进一步加强SMA的全局搜索能力和FPA的局部搜索能力。HASMFP的主要改进工作如下：

a）通过种群中的个体与当前最优个体之间的距离将种群动态划分为黏菌子种群和花粉子种群，黏菌子种群侧重于全局探索，花粉子种群进行深度开发，两个子种群的算法相辅相成，使探索与开发更加平衡。

b）利用相似度与适应度的综合排序感知机制生成选择概率，选择概率随机选择黏菌个体替代原SMA的全局搜索规则中的当前最佳个体，以提高SMA的种群多样性。

c）在异花授粉阶段加入控制莱维飞行的动态权值并融入恒定收缩系数，使改进后的FPA具备更高的整体开发性能，且在自花授粉阶段添加精英引导项来提高FPA的收敛速度与精度。

1 FPA与SMA简介

1.1 FPA

FPA是模拟自然界花朵授粉过程的一种元启发式算法。授粉是将花粉从一朵花转移到另一朵花的过程，可以是生物或非生物的。将生物授粉视为全局授粉，通过动物传播花粉，可在大范围内进行传播；将非生物的自花授粉视为局部授粉，不需要传粉媒介，但传播的范围有限。花朵的授粉过程可以总结为以下四条规律：

a）生物的异花授粉对应算法的探索阶段，全局搜索通过生物充当载体，遵循莱维飞行规律。

b）非生物的自花授粉对应算法的开发阶段，局部搜索是种类植物不同花朵之间通过风实现传粉。

c）繁衍概率即为花的恒常性，繁衍概率的取值大小与两朵花的相似性成正比。

d）利用转换概率p∈［0，1］控制全局和局部授粉的转换。

基于上述规律转换成数学公式进行描述，假定每株植物都只开一朵花且只产生一个花粉配子，使用全局授粉和局部授粉的概念进行花朵个体的进化。

若转换概率rand<p，rand是［0，1］的随机数，则进行全局授粉，花粉的位置更新如式（1）所示。

Xt+1i=Xti+L（Xbest-Xti）（1）

其中：Xt+1i、Xti分别表示第t+1、t次迭代的解；Xbest是当前种群中的最优解；L为步长，服从莱维分布，L的计算如式（2）所示。

其中：Γ（λ）是标准伽马函数，λ=1.5。

若转换概率rand > p，花朵进行局部授粉，此时位置更新如式（3）所示。

Xt+1i=Xti+ε（Xtj-Xtk）（3）

其中：Xtj、Xtk是从种群内部随机选择异于Xti的解，为了确保局部搜索具有更好的开发性，繁殖概率ε对其进行扰动，是［0，1］的随机数，该参数的生成符合均匀分布规则。

1.2 SMA

SMA是模拟黏菌个体的振荡捕食行为的一种元启发式算法。自然界中的黏菌根据空气中食物气味的浓度来接近食物。黏菌静脉接触的食物浓度越高，其振荡越强，黏菌的静脉宽度也会增大，该区域也会吸引更多的黏菌前往；相反，食物浓度较低时，黏菌个体则会探索其他区域。黏菌接近食物的数学公式如式（4）所示。

其中：r是［0，1］的随机数；t为当前迭代次数；Xb（t）为当前获得的最佳位置；XA（t）和XB（t）分别为黏菌种群中随机选择两个个体的位置；X（t）表示当前位置；W为黏菌适应度权重；vb与vc为控制参数，且vb∈［-a，a］， vc从1线性减小到0，参数a和控制变量p的公式如式（5）（6）所示。

a=arctan h（-（t/tmax）+1）（5）

p=tan h|S（i）-DF| i∈1，2，3，…，N（6）

其中：tmax是最大迭代次数；S（i）是当前个体的适应度值；DF为迭代中的最佳适应度值，适应度权重W的公式如式（7）所示。

其中：Sindex是适应度值的排序；r为［0，1］的随机值；Fb和Fω分别为当前迭代过程中获得的最优适应度值和最差适应度值；S（i）表示当前个体的适应度值，i=M表示种群中适应度值排在前一半的个体，i=N表示剩余的个体。

尽管黏菌找到了更好的食物来源，它们仍然会分离一些黏菌个体去探索其他领域，试图寻找到更高质量的食物来源，所以黏菌种群的更新位置数学公式如式（9）所示。

其中：rand为［0，1］的随机数；Ub和Lb分别为搜索区域的上下界；z表示切换概率决定黏菌是围绕当前最佳个体搜索还是探索其他食物源，其他变量同式（4）。

2 基于动态双种群的黏菌和花粉混合算法

为改善单一启发式算法受自身原理的限制出现的探索与开发不平衡的问题，本文HASMFP混合算法将种群动态划分为黏菌子种群和花粉子种群，两个子种群分别使用SMA和FPA独立进行搜索，其中SMA侧重于全局搜索而FPA侧重局部搜索。此外，HASMFP还分别对SMA和FPA进行了改进，以进一步提升SMA的全局搜索能力和FPA的局部搜索能力。

2.1 动态双种群

针对启发式算法中使用单一种群出现的种群多样性较差、收敛效率较低等问题［18］，已有很多学者采用多种群来改善单一种群所出现的问题，如卜冠南等人［19］提出了一种对蚂蚁算法的蚁群进行分组，以及随迭代分组数减少的策略。Deng等人［20］将种群分为两个亚群，每个亚群的大小根据平均适应度值动态调整，增强了算法搜索能力。多种群策略通常将种群划分为2个或者更多的子群，且各子群在同一搜索空间的不同区域分别进行探索与开发，能够显著增强算法的搜索性能。由没有免费的午餐定理［21］可知，任何算法在一类问题上的性能提升都会被在另一类问题上的性能抵消，所以采用多种群策略的算法同样存在上述问题，即算法的全局探索能力得到增强时，会损失一定的局部开发能力。HASMFP采用动态双种群策略，两个子种群分别使用SMA和FPA进行搜索，其中SMA具有更强的全局搜索能力，FPA则具有更强的局部搜索性能。动态双种群依据算法迭代次数动态调整两个子种群的个体数量，对算法整体的探索与开发进行适当的平衡。

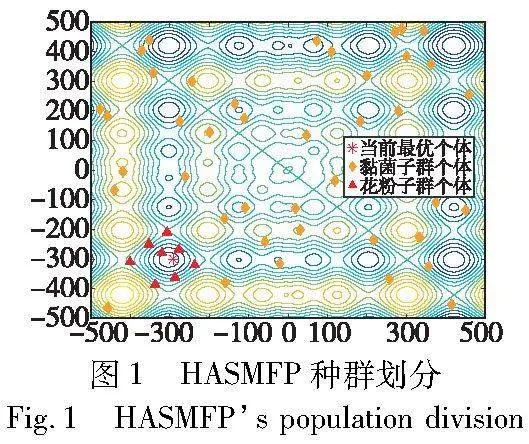
文献［22］发现，处于小范围且有优质解进行搜索引导的环境更适合启发式算法种群的局部开发。基于将种群划分为两个子种群并分别使用SMA在黏菌子种群侧重全局搜索和采用FPA在花粉子种群侧重局部搜索的设计思想，HASMFP先计算种群中的所有个体Xti与当前最优个体Xtbest之间的欧氏距离，如式（10）所示。

其中：Lti表示第t次迭代中第i个个体与当前最优个体的距离；D表示维度。再按距离进行由小到大的排序并依据排序结果将种群划分为花粉和黏菌子种群。即将距离升序排列靠前的个体划入花粉子种群，其余个体被划分为黏菌子种群，并将黏菌子种群的当前最优个体替换为Xtbest，即两个子种群共享最优位置。如图1所示，按上述方法进行种群的划分可以使花粉子种群囊括当前最优个体以及最优个体附近的个体，从而使FPA基于花粉子种群进行高效的局部搜索。同时黏菌子种群中的个体距离当前最优个体较远且更为分散，在提升黏菌种群多样性的同时，还可发挥SMA善于全局搜索的优势并降低算法陷入局部最优的风险。

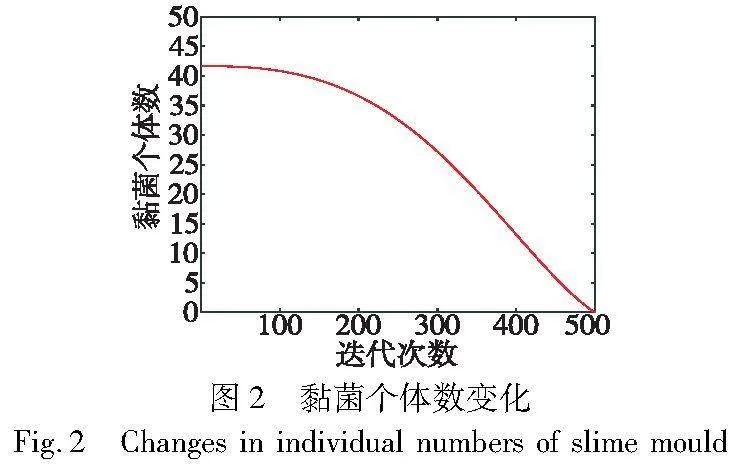
因为算法应该在迭代前期侧重全局搜索以加快收敛速度并在迭代后期侧重局部搜索以提高收敛精度，所以HASMFP采用了一种动态种群划分机制，其中动态双种群的数量变化分别如式（11）（12）所示。

其中：NSMA是黏菌子种群个体数量，且向下取整；NFPA是花粉子种群个体数量；N是划分前的种群规模；t为当前迭代次数；T为算法的最大迭代次数。当种群规模为50时，黏菌子种群的个体数变化为如图2所示的递减曲线。即在算法的迭代前期，确保黏菌子种群包含更多的个体，使HASMFP侧重于依靠SMA使用大种群进行广泛的全局探索。到了迭代后期，黏菌子种群的个体数量降低，而花粉子种群包含更多的个体，可以使算法在最优个体附近进行更为细致的局部搜索，以提高整体的精度，同时黏菌种群仍然包含小数量的个体，从而保证算法仍然具有跳出局部最优的能力。

2.2 改进的SMA

基于上述动态双种群策略，本文将改进的SMA用于黏菌子群，并侧重于全局搜索。根据标准SMA的位置更新式（9），当r<p时，黏菌个体的全局搜索规则取决于当前最佳个体的位置和其他两个随机选择的个体位置，使黏菌围绕在最佳位置附近搜索。黏菌在探索未知食物来源时，基于vb和vc的协同作用来更新其位置，vb的振荡效应增加了全局勘探的可能性，vc是一个从1到0线性递减的参数，搜索机制弱且单一。随着迭代次数的增加，黏菌逐渐向最佳个体位置处聚拢，且vb的振荡效应减弱，将导致种群的多样性随迭代次数的增加而快速降低，使SMA在搜索时易陷入局部最优。针对上述问题，HASMFP采用基于相似度与适应度的综合排序感知策略对原SMA的全局搜索规则进行改进，以提升种群多样性并增强SMA的全局搜索能力。

在每次迭代中，先按向量间的夹角余弦值计算黏菌子种群中的每个黏菌个体与当前最优个体间的相似度Mti：

其中：Xti，j是t次迭代中第i个向量个体的第j维；Xtbest，j是t次迭代中当前最优个体的第j维；D表示维度;Mti越小代表解向量之间的夹角余弦值越小，夹角越大，该个体与当前最优个体相似度越低。

再将黏菌子种群中的所有个体按相似度和适应度分别进行升序排序，得到黏菌个体排序后的相似度序号mi和适应度序号ni，然后按式（14）可得每个黏菌个体的综合排序序号Ri：

Ri=mi+ni（14）

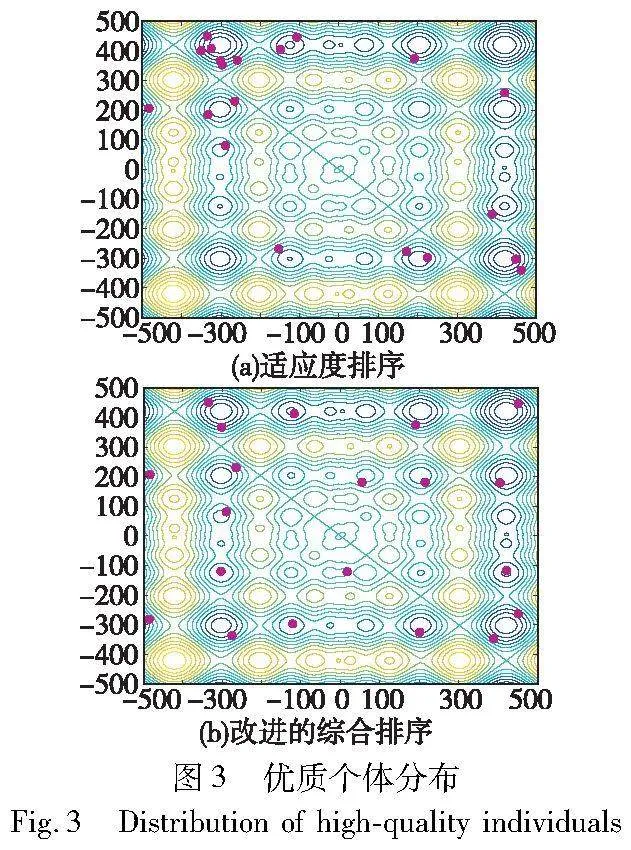
因为mi越小，表示该个体与当前最优个体的差异性越大，并且ni越小则该个体适应度越低，所以Ri越小代表黏菌个体越优质。当前最优个体的相似度序号和适应度序号都为1，所以其综合排序序号也为1，即综合排序为第一。图3（a）（b）分别显示了只按适应度排序和按本文提出的综合排序后排名靠前的若干优质个体分布对比。从图3（a）可看出，只依据个体适应度排序结果选出的优质个体易聚集在一个或多个波谷附近。如图3（b）所示，利用相似度与适应度的综合排序选择出的优质个体具有适应度值低，位置也相对比较分散的特点，所以可以选择那些相似度较低且适应度值小的黏菌个体来替换当前最优个体来进行全局探索，以增加种群多样性并提升算法的探索性能。

在得到黏菌个体的综合排序序号Ri后，HASMFP根据每个黏菌个体的Ri，按式（15）计算该个体被选择的概率Pi，并依据选择概率Pi从种群中随机选择黏菌个体替换原SMA位置，更新式（9）的当前最优个体：

其中：N是黏菌种群规模；Wi为第i个黏菌个体的选择权重。选择权重Wi的计算公式如式（16）所示。

其中：θ为控制选择权重随综合排序序号增加而下降的参数。由式（16）可知，每个黏菌个体的选择权重Wi与综合排序序号Ri为指数关系。选择概率Pi的值只和黏菌个体的综合排序序号Ri有关，排名的范围是从1到N。即确保黏菌个体越优质，其被选中的概率就越大。

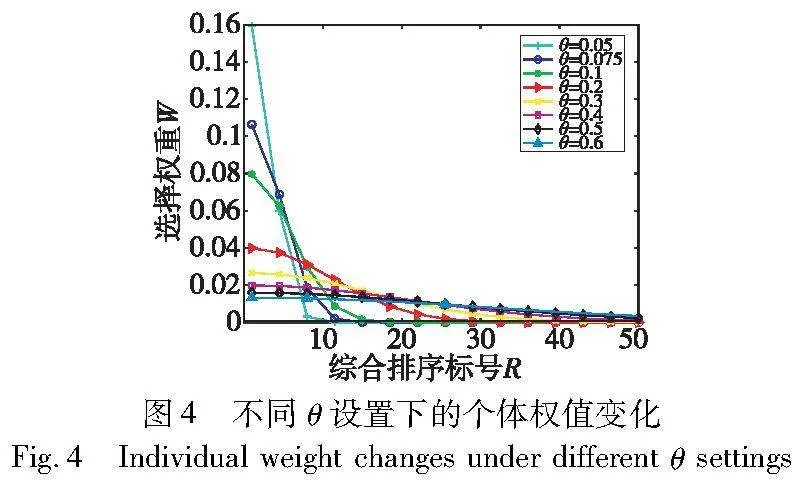
式（16）中的参数θ影响着每个黏菌个体的选择概率。为了更好地观察参数θ产生对选择概率Pi的影响，图4绘制了在不同θ设置下，选择权重随综合排序序号增加的变化曲线。

从图4可知：a）θ值越小，随着综合排序序号增加，选择权重下降的速度越快，即优秀黏菌个体保留更多的选择权重。最终选择权重集中在前几个最优秀的黏菌个体上，使黏菌种群的个体将被引导在几个方向上搜索解空间，可以增强搜索效率。b）θ值越大，随着综合排序序号增加，选择权重下降的速度越慢，黏菌个体的选择权重之间的差距不明显，可以引导黏菌个体从更多元化的方向去寻找最优解，有利于提高种群的多样性。基于上述分析，为了更好地平衡搜索效率和种群多样性，HASMFP将θ设置为0.2，可以使黏菌个体既能够有效地探索解空间，又可以适当地挖掘有潜力的区域。

综上，改进后的SMA全局位置更新规则如式（17）所示。

Xt+1=Xtselect+vb·（W·XtA-XtB） r<p（17）

其中：Xtselect表示第t次迭代中黏菌子种群中通过综合排序感知选择概率得到的优质黏菌个体，其他变量同式（4）。

2.3 改进的FPA

与其他启发式算法类似，花授粉算法到了迭代后期收敛速度变慢，且随着迭代次数的增加，种群多样性减少，算法容易滞留在局部的某个点，出现收敛精度低、探索与开发不平衡等问题。由于莱维飞行具有大小步长概率出现、运动方向多变的特性，可能会因运动步长太大导致最优花粉个体信息的丢失，且花授粉算法在局部搜索中使用的随机差分项具有一定的搜索盲目性，即搜索规则中两个随机个体的差分操作会使算法进行无目的的随机搜索，可能降低算法的搜索效率。针对上述问题，HASMFP对FPA的全局搜索和局部搜索机制进行了改进。

群智能优化算法中，扰动项前面的系数将直接影响算法的最终性能，系数取值过大或者过小都会导致算法过早收敛，采用动态权值可以很好地平衡算法前后期对扰动的需求［23］，HASMFP利用了动态权重值和恒定收缩系数来改进全局搜索。全局搜索公式的改进如式（18）所示。

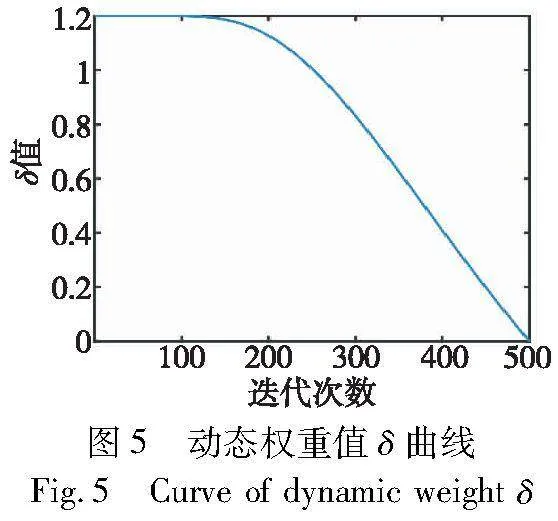
其中：rand是［0，1］的随机数；α是取值为0.01的恒定收缩系数；δ是动态权重，其他变量同式（1）。动态权重δ的定义如式（19）所示。

其中：δmax和δmin分别为参与权重值计算的最大值和最小值；T为算法的最大迭代次数；t是当前迭代次数。如图5所示，δ的值呈一条非线性下降的曲线。在迭代前期δ的值较大，以更强的扰动来寻找优势解，并扩大花粉个体搜索的范围，增强算法的全局搜索能力。δ的值随着迭代次数的增加而逐渐降低，使FPA在迭代后期应由勘探转向开发，降低权重值可以减少无效探索，以优质解为引导进行更小幅度的扰动，提高算法迭代后期的开发能力。FPA使用的莱维飞行会使花粉个体位置更新出现不稳定的大步长扰动［16］，不利于小范围内的局部开发。HASMFP提出使用恒定收缩系数α，来缩小花粉个体由于莱维飞行产生的大跨步探索，使FPA能够专注于局部开发。

HASMFP在FPA的局部搜索机制中添加了精英引导项将花粉个体往更优处引导，以进一步增强FPA的局部搜索效率，FPA局部搜索的改进如式（20）所示。

Xt+1i=Xti+ε（Xtj-Xtk）+（XtA-XtB）（20）

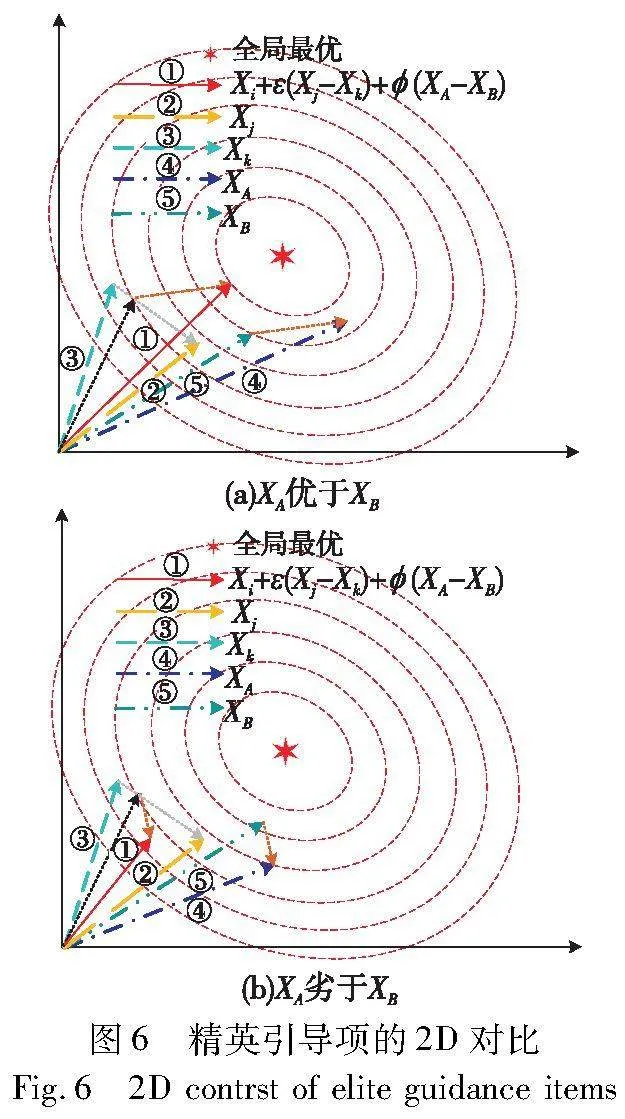
其中：XtA和XtB代表第t次迭代时花粉种群中适应度值排在前一半的两个随机个体，并且XtA的适应度值优于XtB；是［0，1］符合均匀分布的随机数，其他变量同式（3）。式（20）右边的第三项为精英引导项，即将花粉子种群中适应度值排在前一半的个体划分为精英个体，随机选择两个精英个体XA和XB的差分值来组成精英引导项，加快算法的收敛速度。精英引导项选择较优个体XA作为差分中的被减向量，可以将花粉个体往更优位置处扰动，如图6所示。精英个体能够引导花粉子种群中的个体往更优位置靠近，帮助算法找到更优解。式（20）右边的第二项为随机差分项，增加随机差分项使算法具有一定的全局搜索能力，有利于摆脱陷入局部最优导致的搜索停滞。

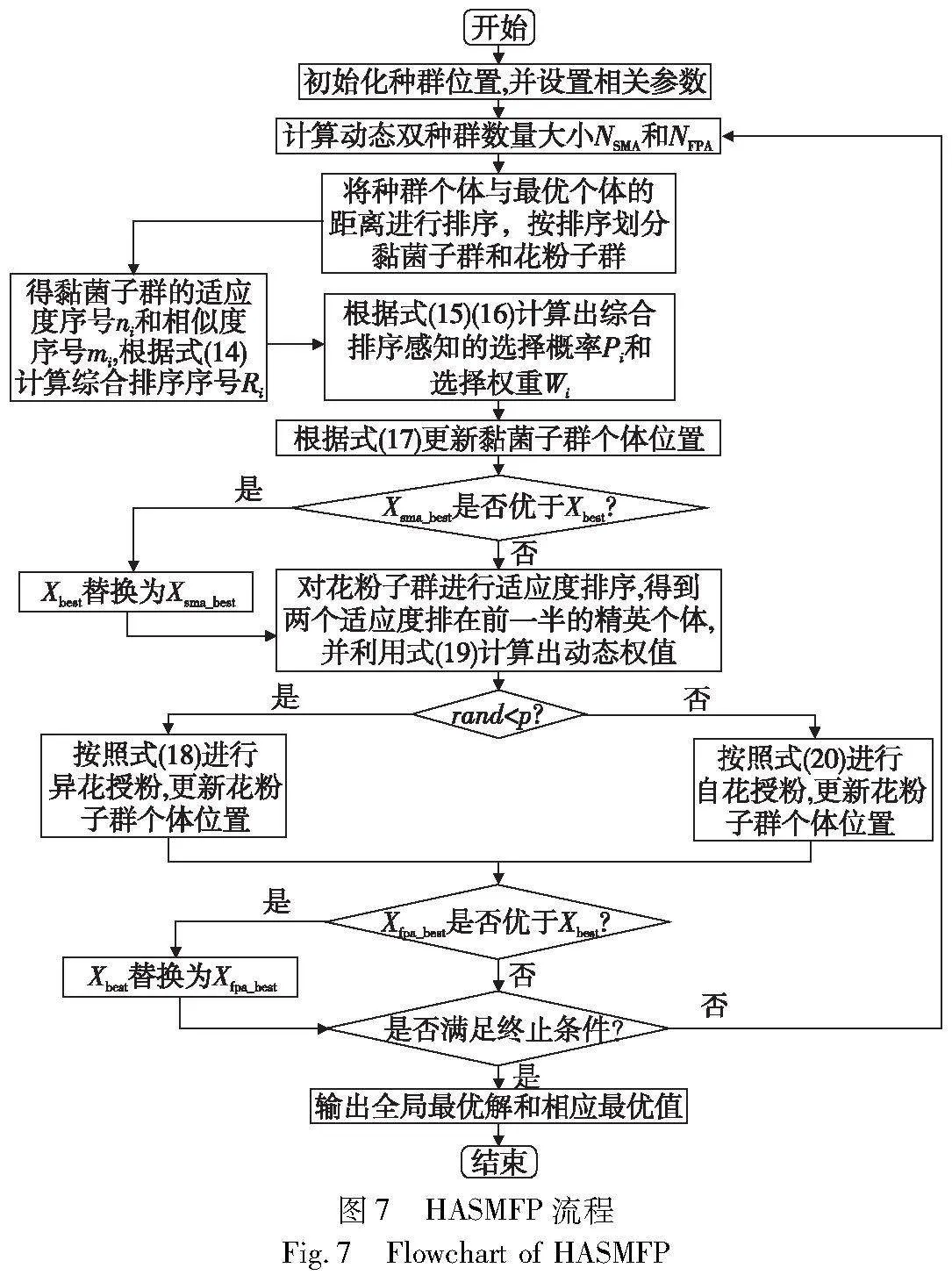
2.4 算法流程

HASMFP流程如图7所示。

2.5 HASMFP时间复杂度分析

标准FPA和SMA的时间复杂度可以表示为O（T×N×D），其中T为算法最大迭代次数、N为种群规模、D为问题维度。设NSMA为黏菌子种群规模、NFPA为花粉子种群规模。HASMFP开始迭代以后，每次迭代按距离排序将种群划分为双种群，增加的时间复杂度为O1（T×N×D）。黏菌子种群的相似度与适应度综合排序增加的时间复杂度为O2（T×NSMA×D），排序后计算相似度序号mi和适应度序号ni所增加的时间复杂度为O3（T×NSMA）。得到相似度序号与适应度序号之后，根据式（14）计算综合排序序号Ri增加的时间复杂度为O4（T×NSMA）。根据式（15）（16）计算选择概率和选择权重增加的时间复杂度分别为O5（T×NSMA）和O6（T×NSMA）。对花粉子种群适应度进行排序，寻找精英个体增加的时间复杂度为O7（T×NFPA）。综上所述，HASMFP的时间复杂度为O8=O（T×N×D）+O1+O2+O3+O4+O5+O6+O7=O（T×N×D）。

3 算法性能测试与分析

3.1 实验设计

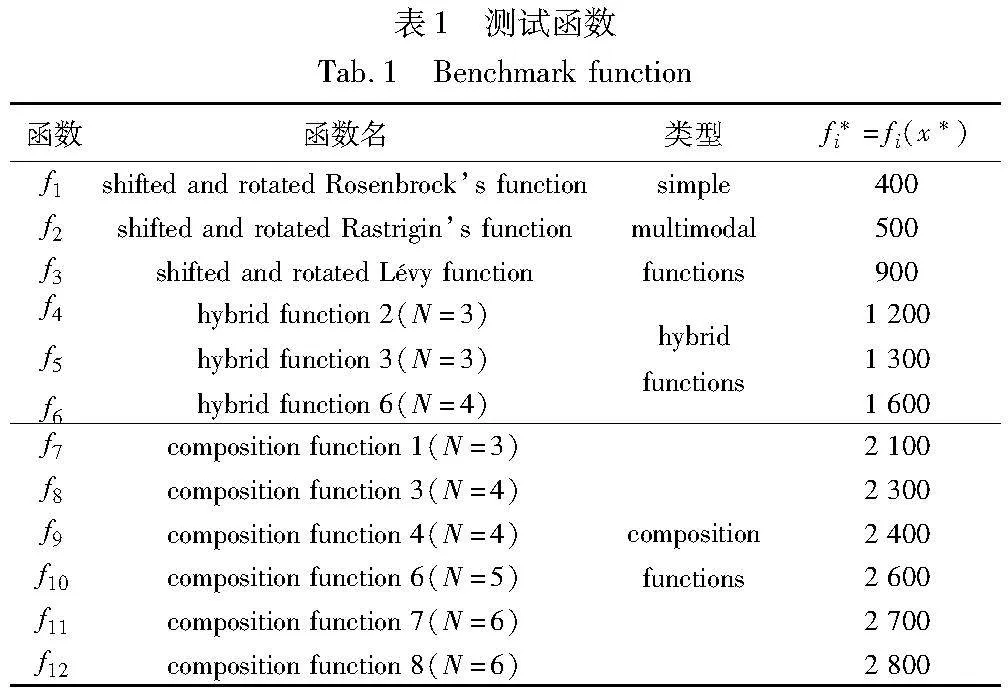
为保障实验的公平性，所有仿真实验均处于同一实验环境中进行。实验仿真软件为MATLAB R2022b，基于AMD R7-5800HS CPU、16.0 GB内存以及Windows 10（64位）的操作系统。本次实验对HASMFP以及其他五个对比算法进行性能测试实验，其他对比算法为ISMA［24］、DTSMA［25］、HLFPA［26］、SCFPA［27］、tMFPA［28］，并且对HASMFP各个策略进行完整性消融实验测试。选取了12个CEC2017中具有代表性的函数作为测试函数，其中包含3个多峰函数（f1～f3）、3个混合函数（f4～f6）和6个复合函数（f7～f12）。选取的所有测试函数都具有大量的局部最优，且随函数复杂度逐渐增加，算法陷入局部最优的可能性也逐步增大。测试集函数如表1所示。

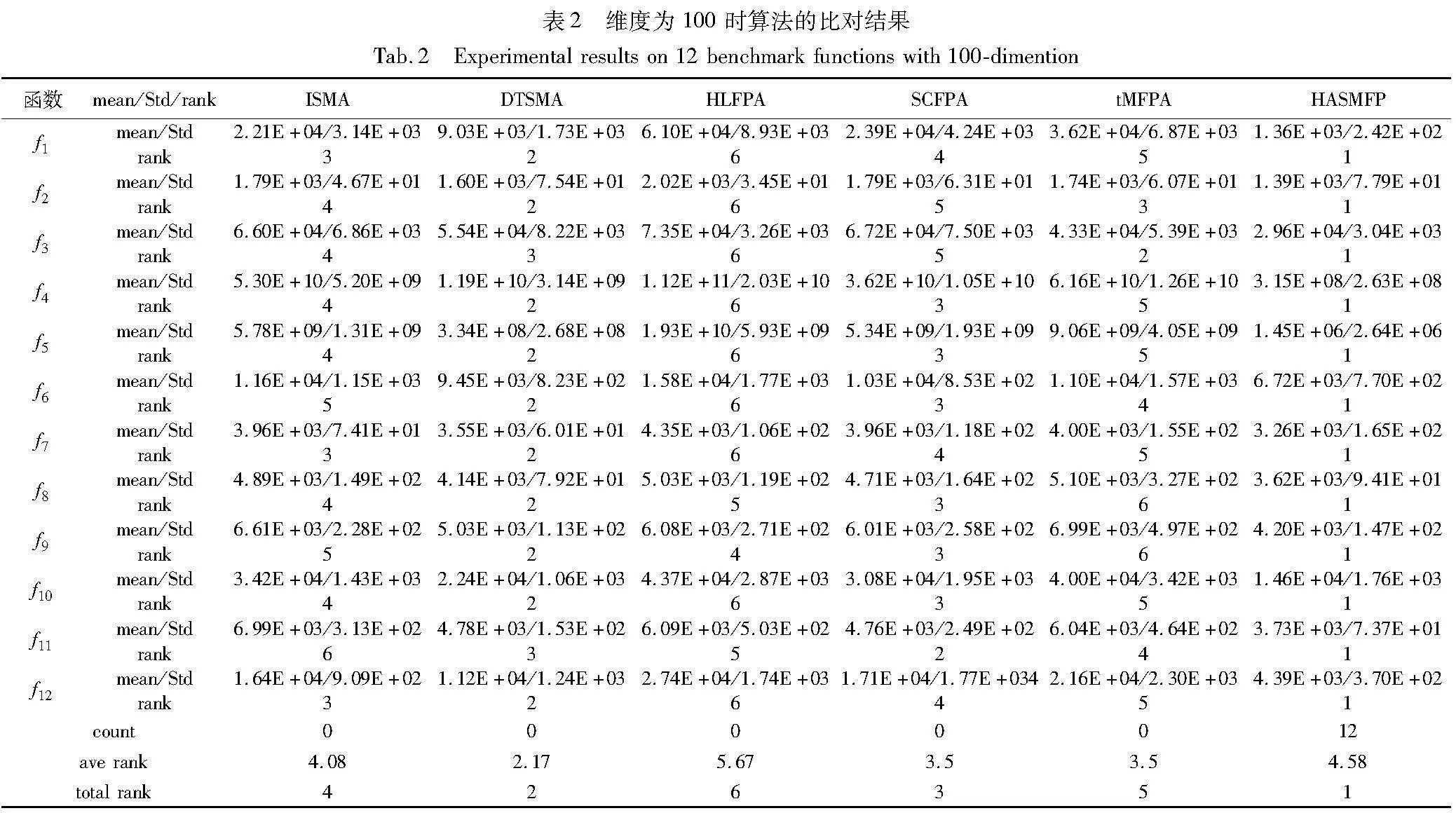
将HASMFP和其他5个对比算法在维度为100维的测试函数上进行测试，算法的迭代次数为500次，各算法独立运行30次。取各算法运行后获得的最优解的均值（mean）、方差（std）以及算法排名（rank）三项指标来评估各算法的稳定性与优化性能。为了保证实验的公平性，各算法的参数设置都和其原论文中一致。极小值问题的求解中，均值越小代表着算法的平均性能越好，方差越小代表着算法性能越稳定。排名的评价标准是均值优先，方差随后。count表示算法排名第一的总次数，ave rank表示算法的平均排名情况，total rank表示基于平均排名来进行最终的排名情况。

3.2 实验结果与收敛曲线对比分析

如表2所示，HASMFP在12个测试函数中收敛精度排名均取得了第一，在total rank总排名中也取得了第一名。HASMFP方差排在实验测试算法中的前列，说明混合算法相较于其他对比算法更具有优势并具有更好的鲁棒性能。HASMFP在f1、f4～f6和f12测试函数上的收敛精度甚至高出其他对比算法一个量级左右。

为了直观对比HASMFP算法和五种对比算法寻优能力的优劣，图8给出了六种算法在100维情况下12个测试函数上的收敛曲线。观察收敛曲线可知，在12个基准测试函数中，HASMFP都具有更好的收敛效果。其中图8（a）～（c）为多峰函数f1～f3的收敛图，可以看出HASMFP的收敛精度要优于其他对比算法；图8（d）～（f）为混合函数f4～f6的收敛图，在算法迭代到100次左右时，HASMFP的收敛精度就超过了其他对比算法，并且随着迭代次数的增加，收敛精度还在不断深入；图8（g）～（l）为复合函数f7～f12的收敛图，从图中可以看出HASMFP具备跳出局部最优的能力，当算法迭代到中后期时，其他对比算法都已经陷入了局部最优。以上表明，HASMFP具备更优的性能。

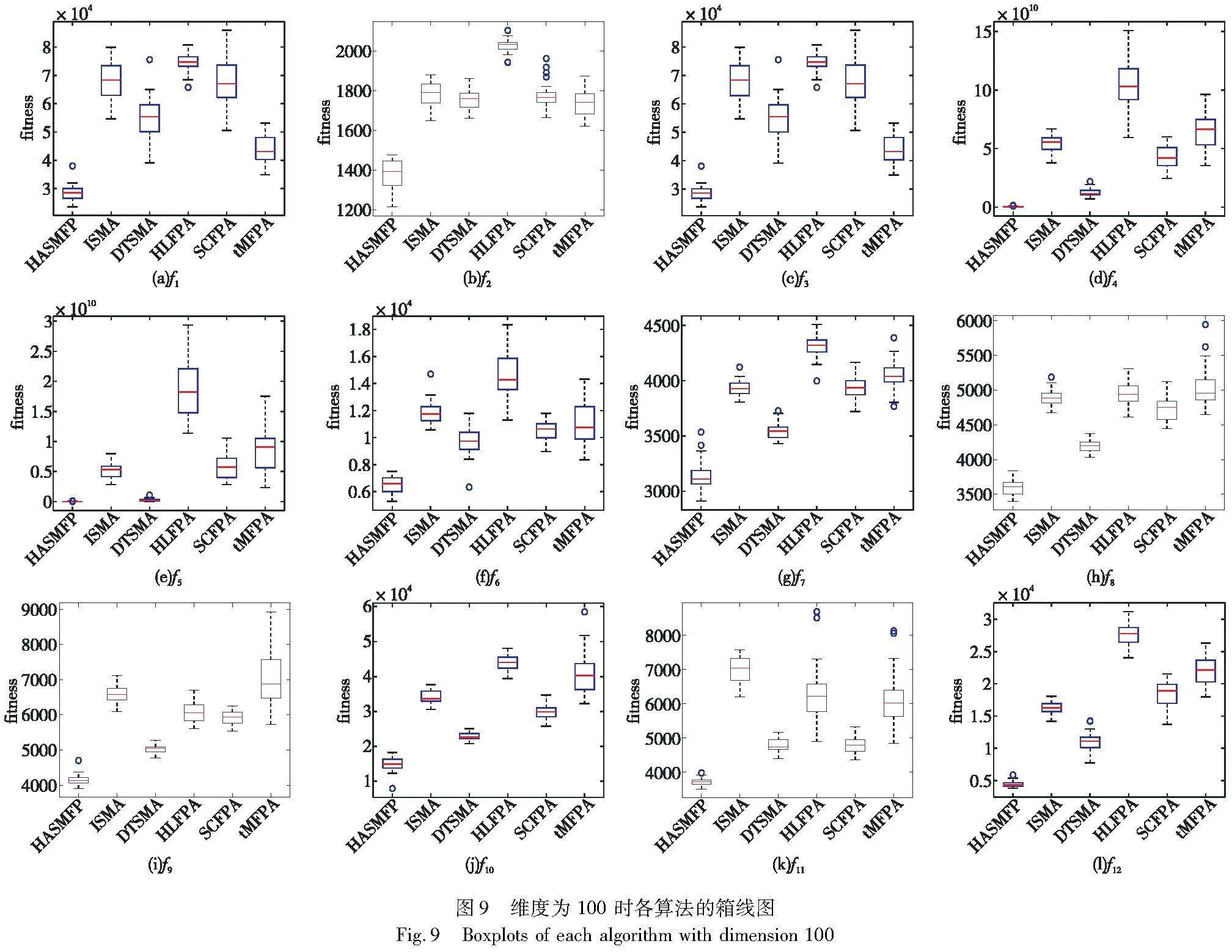
3.3 算法箱线图对比分析

图9包括了HASMFP与对比算法基于上述12个测试函数在维度为100时独立执行30次获得最优解的箱线图。图中箱体高度代表算法最优值的波动情况，箱体底部表示算法的搜索精度。图中除f2和f6以外的函数中，HASMFP箱体较窄，说明HASMFP在这些测试函数中的最优值波动情况小，算法收敛速度较快，导致每一代的最优解之间跨度较小。其他改进算法的箱体较宽，代表算法从迭代开始到结束获取的所有解变化大，鲁棒性比HASMFP弱。同时可明显看出，HASMFP在测试函数中箱体的下限比对比算法更低，代表其搜索精度更高，能够寻找到更优质的解。以上分析表明了HASMFP使用的策略有利于增强混合算法的求解精度与稳定性。

3.4 完整性消融实验

为了验证HASMFP各个策略的有效性，对HASMFP中的改进策略进行完整性消融实验。设将标准FPA和标准SMA按动态双种群混合方式进行混合的算法为HASMFP1，在HASMFP1的基础之上只对黏菌子种群进行改进的算法为HASMFP2，在HASMFP1的基础之上只对花粉子种群进行改进的算法为HASMFP3。将标准SMA、标准FPA、HASMFP1、HASMFP2、HASMFP3和HASMFP基于表1基准函数进行测试，所有算法在维度为100维的函数上进行测试，各算法独立运行30次，迭代次数为500次，各算法参数均保持一致。表3展现了不同改进策略算法收敛精度的情况。

从表3看出，HASMFP1在12个测试函数中的实验结果都优于标准SMA和FPA，表明了动态双种群混合策略的优越性。在黏菌子种群和花粉子种群上各自进行改进的算法HASMFP2和HASMFP3的测试结果优于HASMFP1，说明SMA的改进和FPA的改进对算法有提升。最后HASMFP的测试结果比HASMFP2和HASMFP3都要好，说明将两种算法的改进并混合到一起后，进一步提升了算法的性能。可表明每个策略在混合算法上都是有效的，各个策略都是HASMFP中不可或缺的，共同提升了HASMFP的综合寻优性能。

3.5 Friedman检验

为了进一步验证HASMFP与对比算法的显著差异性，采用Friedman检验［29］对3.1节记录的六种算法进行非参数检验。检验结果如表4所示，表中的P-value表示渐进显著性，是判断各个算法之间是否存在显著性差异的指标，如果该值小于0.01，则表示各项数据之间存在显著性差异。从表4可以看出，对于30维、50维、100维，HASMFP的P-value值分别是2.170 1E-9、4.154 2E-9、1.816 1E-9，都远远小于0.01，说明HASMFP和其他对比算法之间存在显著的差异性。在三种不同维度的Friedman检验中，HASMFP秩的平均值都是最小的，表明HASMFP的性能最佳。综上所述，HASMFP的优化能力在统计学意义上相比于其他对比算法有较大提升。

4 结束语

针对单一启发式算法易受到自身原理的限制导致全局与局部搜索不平衡的问题，提出了一种基于动态双种群的黏菌和花粉混合算法HASMFP。首先，对种群中个体与当前最优个体的距离进行排序，并按排序的距离对种群动态划分为黏菌子种群和花粉子种群。其次，对SMA和FPA进行改进。最后，HASMFP与五种对比算法基于CEC2017中的12个基准测试函数的进行性能测试。实验结果表明，HASMFP在高维度下的测试函数中取得了较好的寻优精度。基于实验数据的Friedman检验进一步验证了HASMFP的有效性。在后续的研究中，将进一步对HASMFP进行改进，并用于解决多目标问题。

参考文献：

［1］Li Shimin， Chen Huiling， Wang Mingjing， et al. Slime mould algorithm： a new method for stochastic optimization［J］. Future Generation Computer Systems， 2020，111： 300-323.

［2］Yang Xinshe. Flower pollination algorithm for global optimization［C］//Proc of International Conference on Unconventional Computing and Natural Computation. Berlin： Springer， 2012： 240-249.

［3］Mareddy P L， Narapureddy S R， Dwivedula V R， et al. Development of scheduling methodology in a multi-machine flexible manufacturing system without tool delay employing flower pollination algorithm［J］. Engineering Applications of Artificial Intelligence， 2022， 115： 105275.

［4］Chen Yang， Pi Dechang， Xu Yue. Neighborhood global learning based flower pollination algorithm and its application to unmanned aerial vehicle path planning［J］. Expert Systems with Applications， 2021， 170： 114505.

［5］Dhal K G， Ray S， Barik S， et al. Illumination-free clustering using improved slime mould algorithm for acute lymphoblastic leukemia image segmentation［J］.Journal of Bionic Engineering， 2023，20（6）：2916-2934.

［6］Yildizdan G， Baykan K. A novel modified bat algorithm hybridizing by differential evolution algorithm［J］. Expert Systems with Applications， 2020， 141： 112949.

［7］Sharma S， Saha A K， Majumder A， et al. MPBOA—a novel hybrid butterfly optimization algorithm with symbiosis organisms search for global optimization and image segmentation［J］. Multimedia Tools and Applications， 2021， 80： 12035-12076.

［8］Talbi E G. A taxonomy of hybrid metaheuristics［J］. Journal of Heuristics， 2002， 8： 541-564.

［9］Abdel-Basset M， Mohamed R， Saber S， et al. Modified flower pollination algorithm for global optimization［J］. Mathematics， 2021， 9（14）： 1661.

［10］Wang Zhongmin， Luo Qifang， Zhou Yongquan. Hybrid metaheuristic algorithm using butterfly and flower pollination base on mutualism mechanism for global optimization problems［J］. Engineering with Computers， 2021， 37： 3665-3698.

［11］吴文斌， 刘志锋， 魏振华. 基于遗传算法的混合花粉算法［J］. 电脑知识与技术， 2017，13（30）：173-175. （Wu Wenbin， Liu Zhifeng， Wei Zhenhua. Hybrid pollination algorithm based on genetic algorithm［J］. Computer Knowledge and Technology， 2017，13（30）：173-175，180.）

［12］Chen Hongmin， Wang Zhuo， Jia Heming， et al. Hybrid slime mold and arithmetic optimization algorithm with random center learning and restart mutation［J］. Biomimetics， 2023， 8（5）： 396.

［13］Samantaray S， Sahoo P， Sahoo A， et al. Flood discharge prediction using improved ANFIS model combined with hybrid particle swarm optimisation and slime mould algorithm［J］. Environmental Science and Pollution Research， 2023，30（35）： 1-28.

［14］Xiong Wenqing， Li Dahai， Zhu Donglin， et al. An enhanced slime mould algorithm combines multiple strategies［J］.Axioms， 2023，12（10）： 907.

［15］Chakraborty P， Nama S， Saha A K. A hybrid slime mould algorithm for global optimization［J］. Multimedia Tools and Applications， 2023， 82（15）： 22441-22467.

［16］Rather S A， Das S. Lévy flight and chaos theory-based gravitational search algorithm for image segmentation［J］. Mathematics， 2023， 11（18）： 3913.

［17］Chakraborty D，Saha S，Dutta O. DE-FPA：a hybrid differential evolution-flower pollination algorithm for function minimization［C］//Proc of International Conference on High Performance Computing and Applications. Piscataway，NJ：IEEE Press， 2014： 1-6.

［18］Liu Jingsen， Liu Li， Li Yu. A differential evolution flower pollination algorithm with dynamic switch probability［J］. Chinese Journal of Electronics， 2019， 28（4）： 737-747.

［19］卜冠南， 刘建华， 姜磊， 等. 一种自适应分组的蚁群算法［J］. 计算机工程与应用， 2021，57（6）：67-73. （Bu Guannan， Liu Jianhua， Jiang Lei， et al. An adaptive grouping ant colony algorithm［J］. Journal of Computer Engineering & Applications， 2021， 57（6）：67-73.）

［20］Deng Lingyun，Liu Sanyang.An enhanced slime mould algorithm based on adaptive grouping technique for global optimization［J］. Expert Systems with Applications， 2023， 222： 119877.

［21］Wolpert D H， Macready W G. No free lunch theorems for optimization［J］. IEEE Trans on Evolutionary Computation， 1997，1（1）： 67-82.

［22］Singh D， Singh U， Salgotra R. An extended version of flower pollination algorithm［J］. Arabian Journal for Science and Engineering， 2018， 43： 7573-7603.

［23］Zhang Hao， Gao Jingyi， Kang Le， et al. State of health estimation of lithium-ion batteries based on modified flower pollination algorithm-temporal convolutional network［J］. Energy， 2023， 283： 128742.

［24］郭雨鑫， 刘升， 张磊， 等. 精英反向与二次插值改进的黏菌算法［J］. 计算机应用研究， 2021，38（12）：3651-3656. （Guo Yuxin， Liu Sheng， Zhang Lei， et al. Elite reverse and quadratic interpolation improved slime mold algorithm［J］. Application Research of Computers， 2021， 38（12）：3651-3656.）

［25］Yin Shihong， Luo Qifang， Du Yanlian， et al. DTSMA： dominant swarm with adaptive t-distribution mutation-based slime mould algorithm［J］. Mathematical Biosciences and Engineering， 2022，19（3）： 2240-2285.

［26］洪露， 贺兴时， 杨新社. 基于三重动态调整的花授粉算法［J］. 西安工程大学学报， 2021，35（2）： 97-103. （Hong Lu， He Xingshi， Yang Xinshe. The flower pollination algorithm based on triple dynamic adjustment［J］. Journal of Xi’an Polytechnic University， 2021，35（2）： 97-103.）

［27］张超， 杨忆. 引入正弦余弦算子和新自花授粉的花授粉算法 ［J］. 西安工程大学学报， 2023， 37（2）： 119-129. （Zhang Chao， Yang Yi. Flower pollination algorithm with introduced sine cosine operator and new self-pollination method ［J］. Journal of Xi’an Po-lytechnic University， 2023，37（2）： 119-129.）

［28］宁杰琼， 何庆. t-分布扰动策略和变异策略的花授粉算法［J］. 小型微型计算机系统， 2021，42（1）： 64-70. （Ning Jieqiong， He Qin. Flower pollination algorithm based on t-distribution perturbation strategy and mutation strategy［J］. Journal of Chinese Computer Systems， 2021，42（1）： 64-70.）

［29］张新明， 姜云， 刘尚旺， 等. 灰狼与郊狼混合优化算法及其聚类优化［J］. 自动化学报， 2022，48（11）： 2757-2776. （Zhang Xinming， Jiang Yun， Liu Shangwang， et al. Hybrid coyote optimization algorithm with grey wolf optimizer and its application to clustering optimization［J］. Acta Automatica Sinica， 2022，48（11）： 2757-2776.）