两阶段机场多特种车辆协同充电调度策略

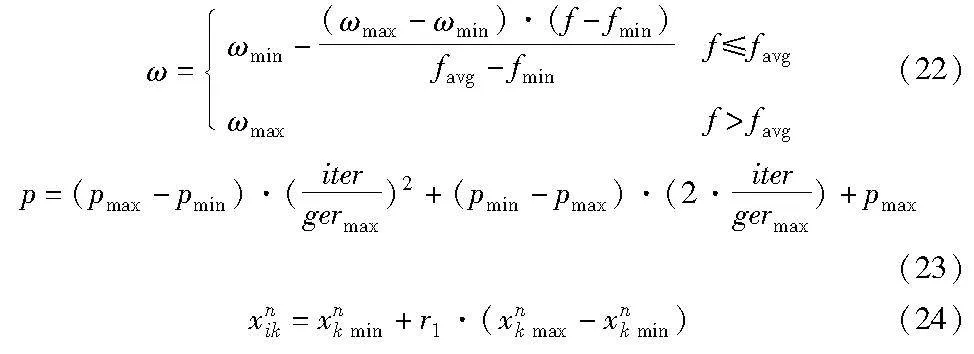
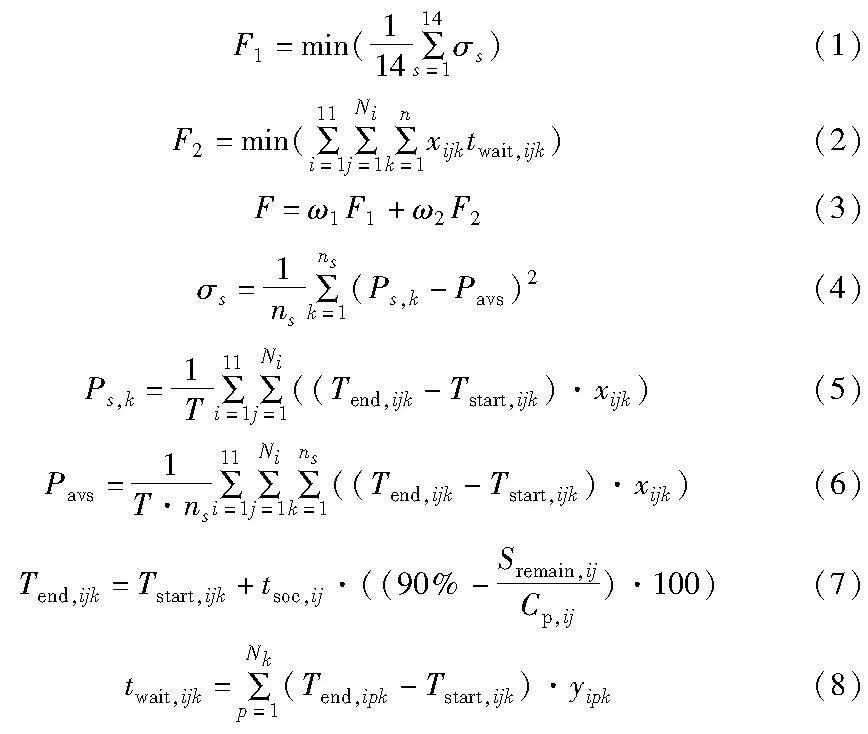
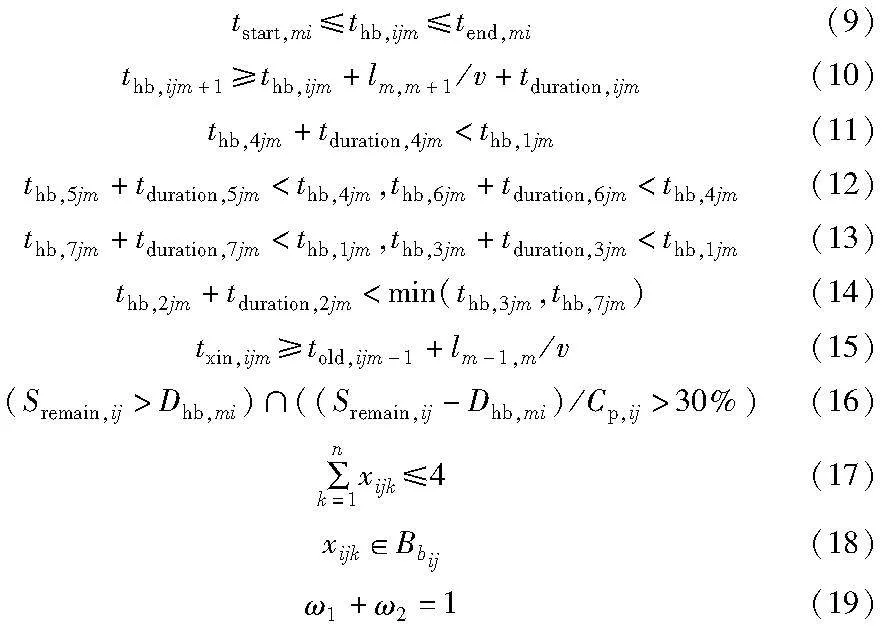
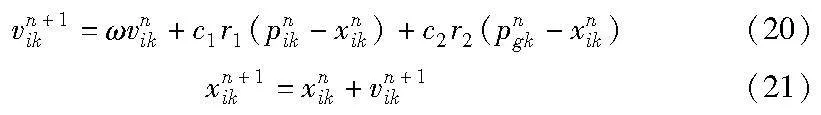
摘 要：在机场区域内，新能源特种车辆充电具有很大的随机性，且不同种类特种车辆充电情况各不相同，造成飞行区内各充电桩利用率相差过大，影响机场配电网的健康运行。针对上述现象，设计了十一车型两阶段特种车辆协同充电调度策略。第一阶段通过分析不同车辆对航班的保障流程，以同一车辆对相邻航班保障起始时间差值最小为目标，生成存在充电需求的车辆序列。第二阶段以减小飞行区各区充电桩时间利用率方差和车辆充电排队时间为目标，在上一阶段车辆序列基础上采用改进的自适应变异粒子群算法进行模型求解，并以国内某枢纽机场的实际车辆充电数据进行对比验证。实验表明，采用该算法后，车辆充电时的等待时间降低了93.5%、飞行区充电桩时间利用率的整体方差下降了88.7%，达到了均衡使用充电桩的目标。

关键词：新能源特种车辆； 充电桩； 充电调度； 改进的自适应变异粒子群算法； 均衡使用

中图分类号：TP391 文献标志码：A 文章编号：1001-3695（2024）07-013-2012-06

doi：10.19734/j.issn.1001-3695.2023.12.0566

Two-stage collaborative charging scheduling strategy forairport multiple special vehicles

Abstract：In the airport area， the charging behavior of new energy special vehicles has great randomness， and the charging conditions of different types of special vehicles are different， which results in a large difference in the utilization rate of each charging pile in the airport area， affecting the healthy operation of electric distribution network of the airport. In response to the above phenomenon， this paper designed a two-stage collaborative charging scheduling strategy for eleven types of special vehicles. In the first stage， this paper analyzed the service process of different vehicles for flights， with the goal of minimizing the difference value in the start time of service for adjacent flights by the same vehicle， and generated a sequence of vehicles with charging needs. In the second stage， the strategy aimed to reduce the variance of time utilization of charging piles and vehicle charging queue time in each zone of the airport area. Based on sequence of vehicles in the previous stage， this paper used an improved adaptive mutation particle swarm optimization algorithm to solve this model， and validated the strategy by comparing it with actual vehicle charging data of a domestic hub airport. The experiment shows that this algorithm can achieve a 93.5% reduction in the waiting time for vehicle charging， and it reduces the overall variance of time utilization of charging piles in the airport area by 88.7%. Finally， this strategy achieves the goal of balanced use of charging piles.

Key words：new energy special vehicles; charging pile; charging scheduling; improved adaptive mutation particle swarm optimization algorithm; balanced use

0 引言

民航业对建设现代化进程的交通强国起重要发展作用，是支撑交通运输现代化的重要战略性产业，未来会更加重视民航业的高质量健康发展［1］。同时，为应对全球气候变暖趋势逐步加剧的现象，在民航业健康发展的期间要统筹绿色发展［2］。机场区域推广使用新能源车辆，以及全面实施“油改电”工作，对未来打赢蓝天保卫战和建设绿色机场具有重大意义［3］。

不同于传统的燃油特种车辆调度，新能源特种车辆在满电情况下的续航能力要远小于燃油车辆［4］，基本上进行几次航班服务就会产生充电需求，如不建立相应的充电策略，在未来大规模使用新能源车辆情况下产生的大量充电需求可能就会影响车辆的正常充电以及充电桩的健康使用。因此建立合理的机场新能源车辆充电调度策略，对未来提升航班保障效率具有非常重要的研究价值［5］。

目前，国内外专家对车辆充电调度的研究主要涉及城市交通方面，针对机场区域的新能源特种车辆的研究则相对较少。

基于常规民用电动汽车有序充电调度方面，Rakibul等人［6］为解决电动货运车辆的交货时间紧张、充电时间长等问题，建立了混合整数线性车辆路径规划模型，以系统总成本、配送延迟成本等最小为目标进行优化求解。针对解决电网削峰填谷的问题，相关学者采用了电动汽车入网充放电调度策略［7～9］。Pelletier等人［10］为探究电池老化、电网限制以及能源成本等对电动汽车充电的影响，建立了一个综合数学模型并进行评估。Stephen等人［11］针对车辆充电效率低下的问题，设计了一种自动引导车辆的充电调度策略。Zhou等人［12］为保障电力系统的正常运行，建立了一种车辆协调充电调度优化模型，适应了未来微电网的快速发展。

基于机场特种车辆方面，Liu等人［13］为解决地面特种车辆数目不足的问题，建立了以特种车辆数目需求最小和时间成本最小为目标的双目标车辆规划模型，充分利用了现有特种车辆资源。Zhu等人［14］建立了关于加油车以及摆渡车的多目标混合整数规划模型，有效解决了航班延误问题。Zhou等人［15］提出了一种学习辅助领域搜索方法，并用于求解车辆路径模型问题。对于机场内电动特种车辆充电调度方面的研究，只对电动车辆的充电问题进行了考虑，没有结合不同特种车辆对航班的保障服务次序，无法体现航班保障服务的严谨性［16～18］。

飞行区特种车辆的研究大多基于单车单航班服务的车辆调度方式，且大多针对燃油车辆，很少涉及新能源车辆的调度策略。而在飞行区内，大多数车辆采用就近充电方式，在航班密集处的充电桩会过负荷使用，航班较少处的充电桩会大量闲置，充电桩的不均衡使用可能会影响机场配电网的健康运行。因此，本文在飞行区内各新能源车辆严格遵循其服务航班次序的基础上建立多特种车辆充电调度模型，并采用了改进的自适应变异粒子群算法进行模型求解。仿真结果验证了该模型的可行性。

1 问题描述

在飞机离港前，需要一系列特种车辆对航班进行协同保障服务［19］，本文主要针对近机位航班保障需要的11种特种车辆进行相关研究，包括飞机污水车、飞机清水车、飞机垃圾车、行李牵引车、平台车、传送带车、飞机牵引车、纯电动客车、纯电动轿车、纯电动多用途乘用车、纯电动多用途货车。

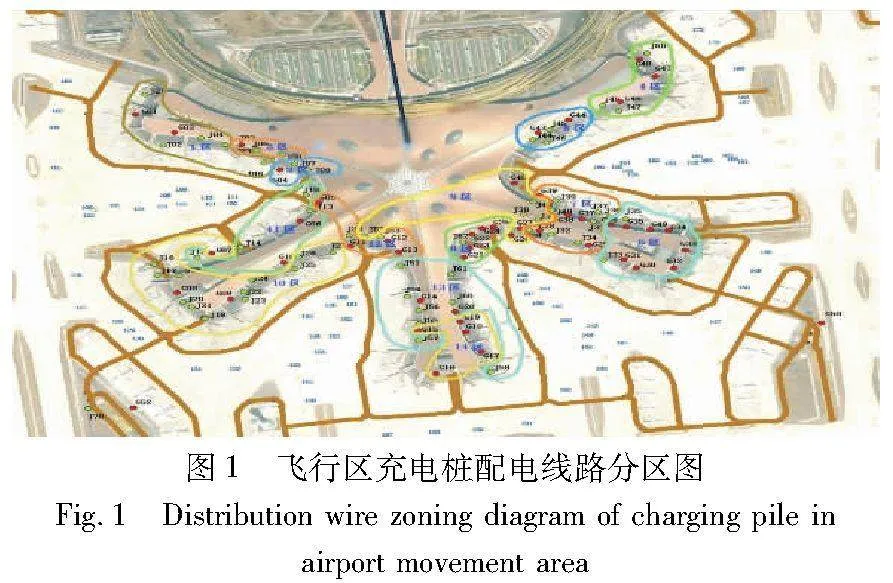
本文设计一种两阶段多特种车辆协同充电调度策略，其作用是在多种特种车辆按相应的顺序保障完航班的基础上，对有充电需求的特种车辆进行有序的充电调度。通过对国内某枢纽机场飞行区内的充电桩配电线路进行实际调研，将这些充电桩按照不同的配电线路分为14个区，在不同分区里对车辆进行充电调度，如图1所示，图中曲线圈着的为划分的各个分区，其中G01-J62为充电桩编号，101-198为机位编号，较粗的线段表示特种车辆在飞行区的行驶路线，车辆只能在该路线上行驶。

第一阶段以车辆保障的相邻航班保障起始时间差值最小为目标，生成不同车辆充电预计时间序列和车辆充电前保障最后一个航班所在机位序列，第二阶段对生成有充电需求的新能源车辆按就近充电原则，依照上一阶段生成的机位，在距离最近的几个分区中选择相应的充电桩进行充电，并采用飞行区各区充电桩时间利用率方差最小和新能源车辆充电等待时间最短的调度策略。

2 特种车辆充电调度建模

2.1 模型假设

假设在时间周期T内，某机场共有N个航班需要保障，能进行保障的各特种车辆数目固定，且已知需要保障的航班机型、航班所在机位以及航班的预计开始时间等信息。

针对飞行区车辆的运行特点，对提出问题作出以下假设：

a）所有特种车辆在充电前进行判定，只有车辆剩余电量够保障下一个航班且车辆保障完下一个航班剩余电池容量大于30%时（电池容量在30%时处于平台区，此状态充电对电池寿命好，当低于30%充电时可能会缩短电池使用寿命，并且可能造成车辆行驶时突然断电现象），才能对该航班进行保障任务，否则前往相应充电桩充电。

b）所有车辆在飞行区内匀速行驶，行驶速度为15 km/h（根据民用航空行业标准，在机场飞行区车辆专用车道区域内，车辆最高的行驶速度不能超过25 km/h，车辆转弯速度限制为15 km/h，考虑安全性，本文取车辆平均行驶速度15 km/h）。

c）每种特种车辆的数目都是有限固定的。

d）车辆充电到剩余电池容量达到90%时结束（车辆充电到90%对延长电池寿命以及提高车辆续航能力效果最好）。

e）飞行区没有低压充电桩，低压特种车辆只能在高低压兼容充电桩充电，而高压特种车辆能在所有充电桩充电（目前国内大多数机场取消了低压充电桩的使用）。

f）车辆前往充电桩充电的初始位置是其保障最后一个航班的所在机位（飞行区内车辆对航班是连续服务的）。

g）特种车辆的初始电池容量在35%～80%随机分布（根据机场实际调研，处于工作中的特种车辆电池容量基本分布在35%～80%，故初始电池容量设置在这个范围）。

2.2 模型符号及参数说明

输入变量：v表示特种车辆在飞行区行驶的速度，为15 km/h;tstart，mi表示第m个航班允许第i种特种车辆保障的最早开始时间；tend，mi表示第m个航班允许第i种特种车辆保障的最晚开始时间；thb，ijm 表示第i种特种车辆的第j辆车保障第m个航班的开始时间，i=1，2，…，11，依次代表飞机牵引车、行李牵引车、传送带车、飞机清水车、飞机污水车、飞机垃圾车、平台车、纯电动多用途乘用车、纯电动多用途货车、纯电动轿车和纯电动客车；tduration，ijm表示第i种特种车辆的第j辆车保障第m个航班所需要的时间；txin，ijm表示第i种特种车辆的第j辆车保障完一组航班，充满电后保障第m个航班的开始时间；told，ijm-1表示第i种特种车辆的第j辆车在保障的上一轮航班组中保障最后一个航班的结束时间；Dhb，mi表示第i种特种车辆保障第m个航班所需要的电量；Sremain，ij表示第i种特种车辆的第j辆车的剩余电量；Cp，ij表示第i种特种车辆的第j辆车的电池容量；lm，m+1表示第m个航班所在机位与第m+1个航班所在机位之间的距离；bij表示第i种特种车辆的第j辆车保障完最后一个航班所在机位；Bbij表示在bij机位的车辆充电所能前往的充电桩集合；s表示将飞行区的所有充电桩按不同的配电线路分为14个区，s=1，2，…，14;ns表示第s区内的充电桩个数；σs表示第s区内的所有充电桩时间利用率方差；Tend，ijk表示第i种特种车辆的第j辆车到第k个充电桩充电的结束时间；Tstart，ijk表示第i种特种车辆的第j辆车到第k个充电桩充电的开始时间；twait，ijk表示第i种特种车辆的第j辆车到第k个充电桩的等待时间；tsoc，ij表示第i种特种车辆的第j辆车充电1%soc（剩余容量占电池容量的比值）时需要的时间；T表示一天中的时间，取值为1 440 min；n表示充电桩的数目，总共为108个；Ni表示第i种特种车辆的个数；Nk表示第k个充电桩需要充电的车辆个数；N表示需要保障的航班个数。决策变量为

2.3 目标函数和约束条件

该模型的目标函数说明如下：

该模型的约束条件说明如下：

式（1）表示飞行区各区充电桩时间利用率方差最小的目标函数；式（2）表示飞行区所有特种车辆充电等待时间最短的目标函数；式（3）为最终的多目标函数，同时考虑分区充电桩时间利用率方差最小，以及车辆充电等待时间最短；式（4）为第s个分区的充电桩时间利用率方差表达式；式（5）为第s个分区内的第k个充电桩时间利用率表达式；式（6）为第s个分区的充电桩平均时间利用率表达式；式（7）为特种车辆的充电结束时间表达式；式（8）为特种车辆的充电排队时间表达式；式（9）表示每个航班服务的特种车辆只能在其对应的时间窗内服务；式（10）表示某个特种车辆只有在下一个航班服务开始时间大于等于上一个航班结束时间和两个航班所在机位路程行驶时间之和时，才能对下一个航班进行服务；式（11）表示飞机牵引车服务必须在飞机清水车服务完成后才能进行；式（12）表示飞机清水车服务必须在飞机污水车服务和飞机垃圾车服务都完成之后才能进行；式（13）表示飞机牵引车服务必须在平台车服务和传送带车服务都完成之后才能进行；式（14）表示传送带车服务和平台车服务都要在行李牵引车服务完成之后才能进行；式（15）表示某个特种车辆服务完一组航班，充满电服务下一个航班时，其开始时间要大于其充电前服务的一组航班中最后一个航班服务完成时间和该两个航班所在机位路程行驶时间之和；式（16）表示只有当车辆剩余电量够满足该航班保障所需电量以及车辆保障完该航班剩余电池容量大于30%时，才能对该航班进行保障任务；式（17）表示每个充电桩在同一时刻最多能对4辆特种车辆进行充电服务，飞行区主要存在两种充电枪数量的充电桩，一种具有2个充电枪，最多可以为2台车进行充电，另一种具有4个充电枪，最多可以同时为4台车进行充电；式（18）表示车辆充电前必须在其机位对应的最近几个分区中选择相应的充电桩充电，不能越界到其他分区；式（19）中ω1、ω2为目标函数F1、F2的加权系数，根据不同优化目标调整相应的值。

3 机场多特种车辆充电调度模型求解

3.1 采用的优化算法

本文设计的车辆协同充电调度策略中需要求解的目标函数是一个多维的，且非线性的问题。对这类多维优化问题，很难用普通的数学方法得到精确的解。在众多智能优化算法中，本文采用最适合该策略的粒子群优化算法（particle swarm optimization，PSO）进行求解［20］。PSO算法的基本原理是：将一组随机粒子（随机解）初始化，并通过迭代找到最优解。在每次迭代中，通过更新式（20）（21），不断更新极值，使空间中的解向最优解的方向移动，当满足所有条件之后，进而输出最优解［21］。

其中：i表示粒子编号；n表示迭代次数；k表示变量维数；vnik表示第i个粒子中第k维在第n代的更新速度；xnik表示第i个粒子中第k维在第n代的值；pngk表示第n代前的种群最优位置；pnik表示第i个粒子在第n代前的个体最优位置；c1、c2为学习因子；ω为惯性权重；r1、r2为0～1的随机数。

由于标准PSO算法存在容易陷入局部最优的特点，不易搜寻到全局最优解。为了平衡PSO算法的局部优化能力和全局搜索能力，本文采用了改进的自适应变异PSO算法（improved adaptive mutation particle swarm optimization algorithm，IAMPSO）［22］。IAMPSO算法将PSO算法中的惯性权重ω改为了式（22），并采用了变异因子p，用式（23）表示，对随机数大于p的粒子用式（24）进行进一步更新。

其中：f表示粒子当前的目标函数值；ωmax表示ω的最大值；ωmin表示ω的最小值；favg表示粒子群的平均目标函数值；fmin表示粒子群的最小目标函数值；xnk min表示在第n代中第k维粒子的最小值，xnk max表示在第n代中第k维粒子的最大值；pmax表示最大变异因子；pmin表示最小变异因子；iter表示当前迭代次数；germax表示最大迭代次数。可以看出，惯性权重ω随着粒子的目标函数值发生变化，当各粒子的目标值接近局部最优时，惯性权重会增大，当粒子的目标值分散时，惯性权重会减小，并且变异因子p在迭代过程中以非线性方式逐渐减小，在初始迭代时更注重搜寻全局最优值，迭代末期则能加大局部最优解搜寻力度，有效提升了算法求解全局最优解的精准度。

引入学习因子变化系数m，当适应度值连续m代不发生变化时，由式（25）更新学习因子，减小算法陷入局部最优的可能。

c1=2·c1，c2=0.5·c2（25）

3.2 算法求解步骤

a）随机初始化种群中的所有粒子参数，包括粒子速度、粒子位置、种群规模、迭代次数等；b）计算各粒子的适应度，将当前迭代状态中的每个粒子适应度值存放在各粒子的pbest中，将pbest中最优的适应度值存放在gbest中；c）用式（20）（21）更新粒子的位置和速度；d）用式（22）更新惯性权重ω，式（23）更新变异因子p；e）对随机数大于变异因子p的粒子用式（24）进行自适应变异；f）将每个粒子的适应度值和经历过的最好适应度值作比较，如果较好，则将其作为目前的最好适应度值，并比较目前所有pbest值和gbest值，更新gpest；g）判断适应度值，如果连续m代没发生变化，则用式（25）更新学习因子；h）如果满足预定的最大迭代次数，则终止搜索，输出结果，否则返回到步骤c）进行再一次搜索。

3.3 特种车辆充电路径调度步骤

飞机离港前，不同电动特种车辆对航班的协同保障及对电动特种车辆进行充电调度的具体步骤如下：a）对某日机场的航班离港时刻，场内空闲电动特种车辆情况进行统计；b）车辆保障完下一个航班电池容量小于30%时视为有充电需求，依照不同电动特种车辆保障航班耗电量、车辆工作前初始电量以及不同车辆航班保障次序，生成所有车辆充电需求数据；c）根据车辆充电需求数据设定IAMPSO算法参数，其中，种群规模设置为500，迭代次数设置为600；d）种群采用整数编码，种群维度为充电车辆数目×充电桩数目，粒子中每个维度的数据表示车辆前往的目标充电桩编号，计算种群初始适应度，适应度值为式（3）所求值，即飞行区各区充电桩时间利用率方差平均值和车辆充电等待时间的加权平均值，越小表明飞行区充电桩利用情况越好，不断对比寻优，找到最优的适应度值和对应的种群位置；e）判断是否达到迭代次数，如果没有达到，则转到步骤d）更新调度策略，并将迭代次数增加1，如果达到迭代次数，则输出最优的车辆充电调度策略。

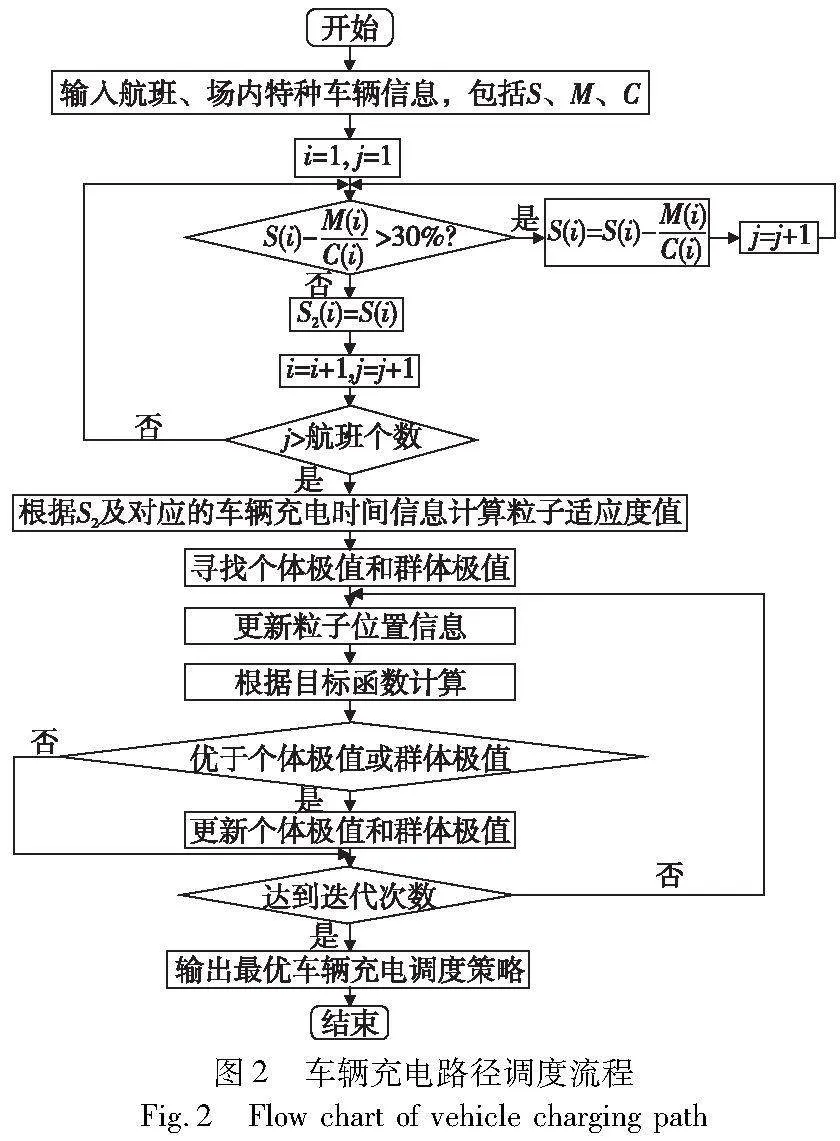
整体的工作流程如图2所示。其中，S为输入的车辆初始电量矩阵；M为车辆保障航班的耗电量矩阵；C为车辆电池容量矩阵；S2为存在充电需求的车辆剩余电量矩阵。

最后对算法优化效果的评价指标如式（26）所示，为方差下降率，其值越高，表明该算法相比于无序充电情况的优化效果越好，对目标函数的求解精度越高。

Fd=（σold，s-σoptimize，s）/σold，s（26）

其中：σold，s为优化前在无序充电情况下的第s个分区的充电桩时间利用率方差;σoptimize，s为采用算法优化后的第s个分区的充电桩时间利用率方差。

4 仿真实验和结果分析

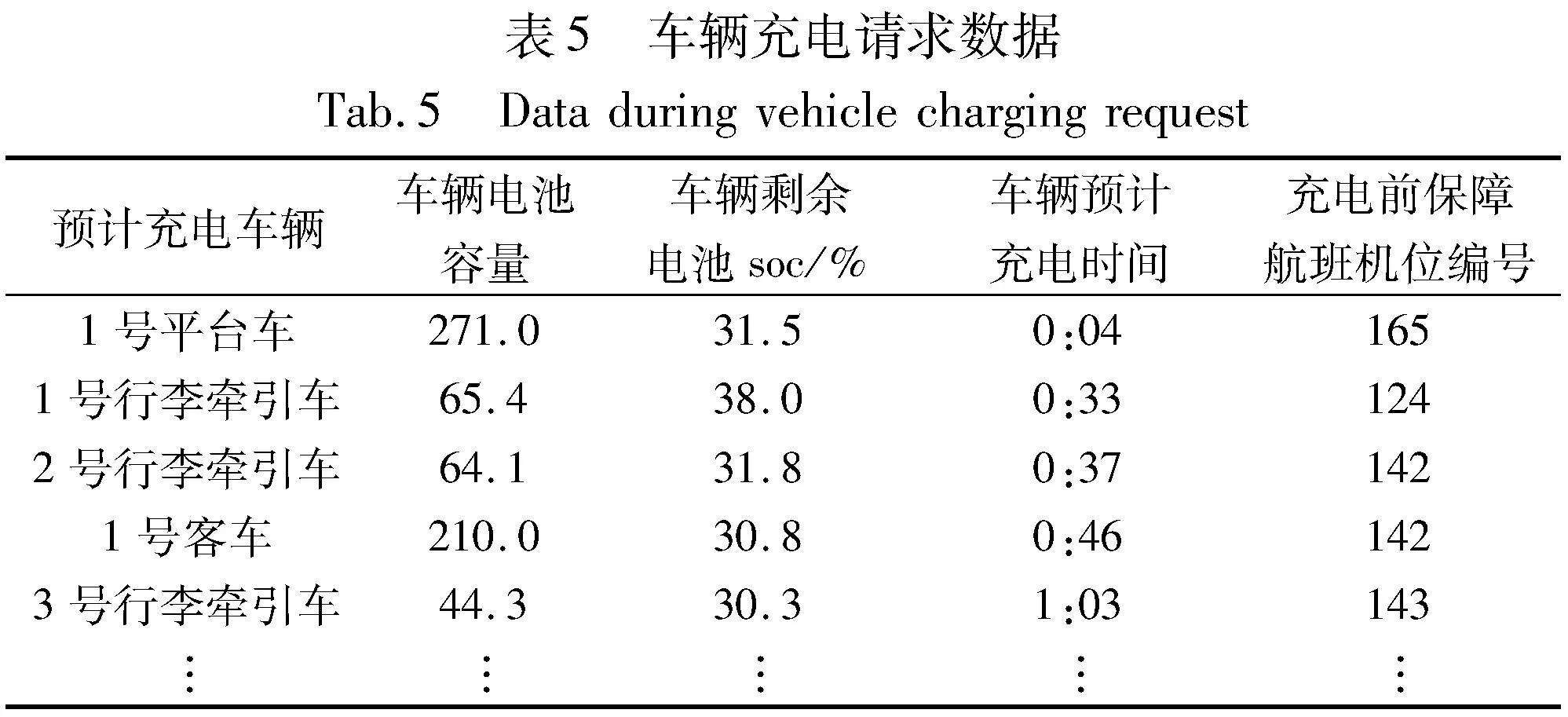
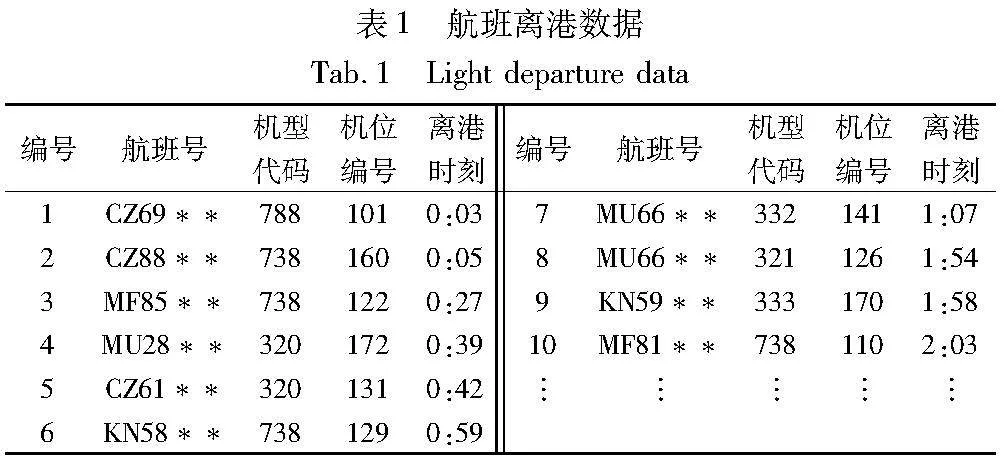
针对两阶段多特种车辆协同充电调度策略，本文通过MATLAB R2018a软件进行仿真。将国内某枢纽机场2021年9月1日全天的航班离港数据代入该模型，生成车辆充电调度结果，与该枢纽机场2021年9月1日全天的充电桩充电数据进行对比实验，最终验证了车辆调度模型和应用IAMPSO算法的可行性，该机场在2021年9月1日的部分航班离港数据如表1所示。

4.1 新能源车辆数据

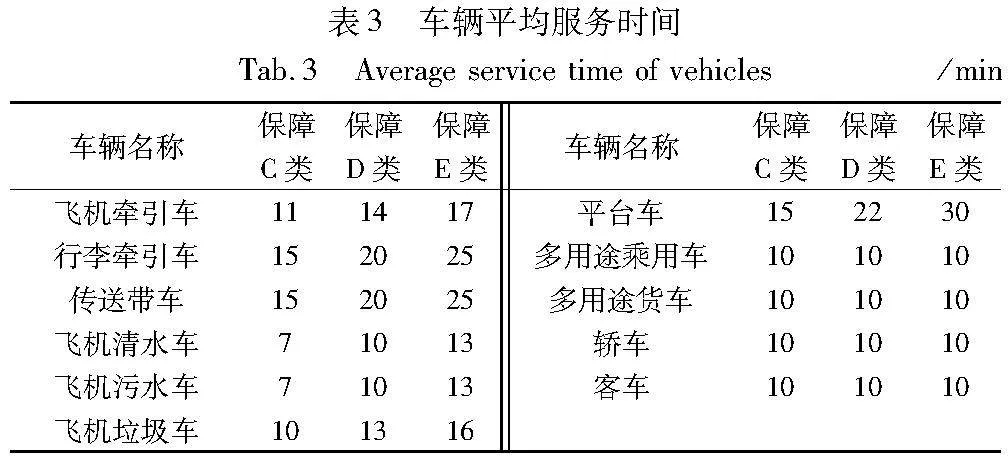
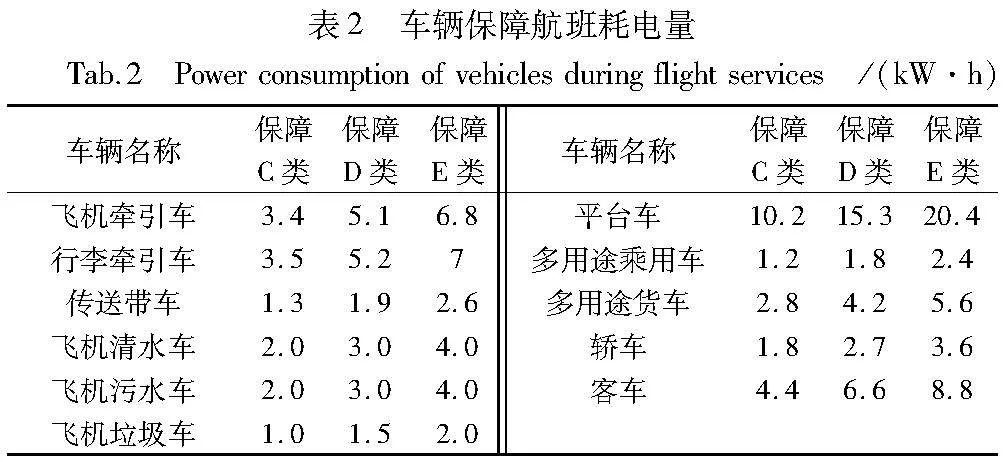
该机场的新能源车辆情况如下：共有飞机牵引车41辆、行李牵引车307辆、传动带车84辆、飞机清水车20辆、飞机污水车20辆、飞机垃圾车6辆、平台车19辆、纯电动多用途乘用车20辆、纯电动多用途货车92辆、纯电动轿车90辆、纯电动客车90辆。共有789辆新能源车辆可为近机位航班保障进行仿真，同时车辆初始电量在35%～80%随机分布。由于航班机型不同，同种车辆保障不同航班耗电量会存在相应差别，其中，航班机型主要分为C类、D类和E类，通过统计该机场2021年7月1日～2021年9月30日的车辆保障航班数据以及车辆充电数据，计算得到不同车辆保障航班的耗电量，如表2所示。同时，不同车辆对航班保障的平均服务时间也不相同，对该机场进行实地调研得到车辆的平均服务时间，如表3所示。

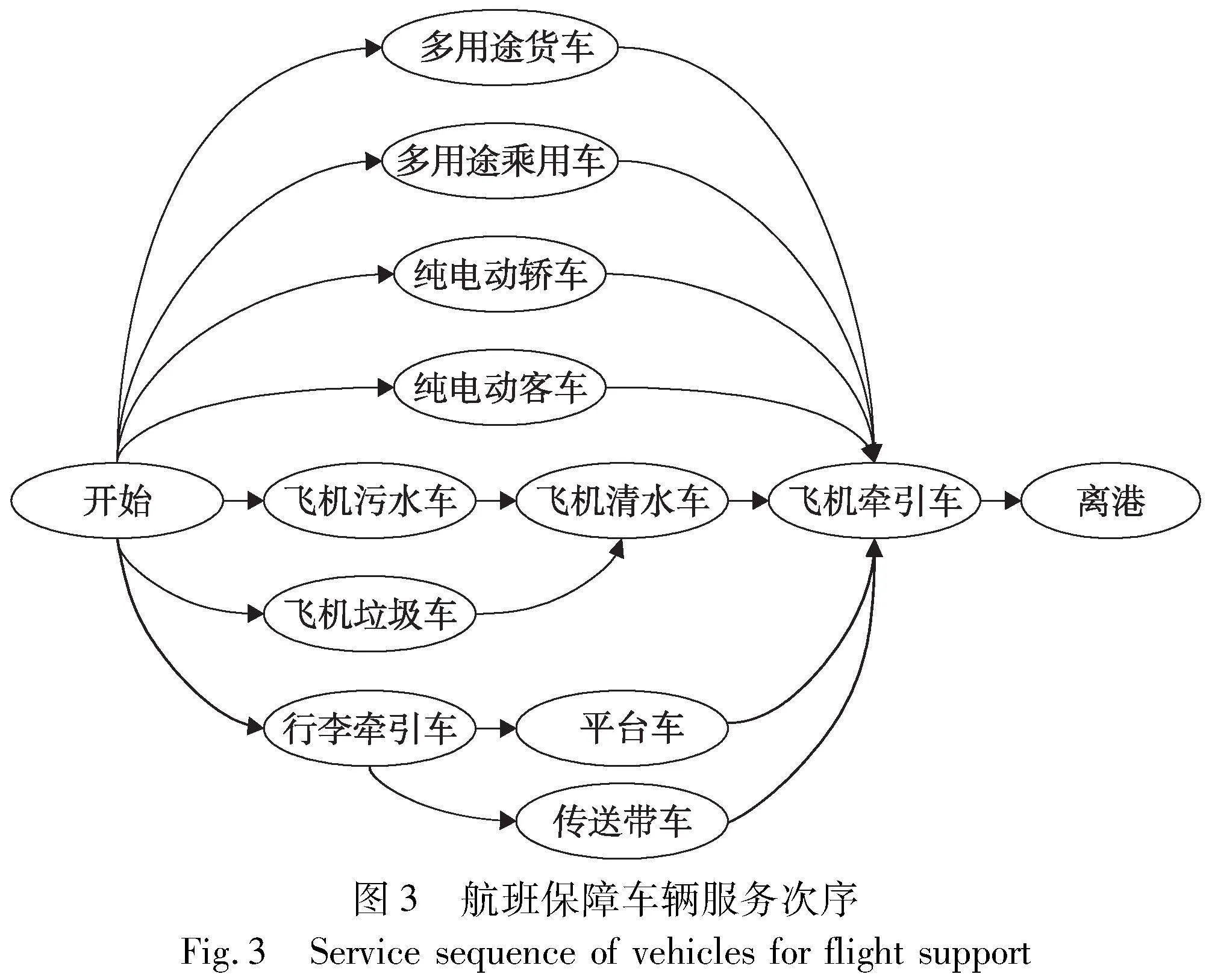
根据《航班安全运行保障标准》，该11种特种车辆在航班离港前进行地面保障服务时要遵循相应的顺序，其中，飞机牵引车在所有车辆服务后进行保障服务；飞机清水车要在飞机污水车和飞机垃圾车服务后进行保障服务；行李牵引车要在平台车和传送带车服务前进行保障服务；而多用途乘用车、多用途货车、轿车和客车则不需要考虑相应的服务次序。对应的不同车辆对航班的服务次序如图3所示。

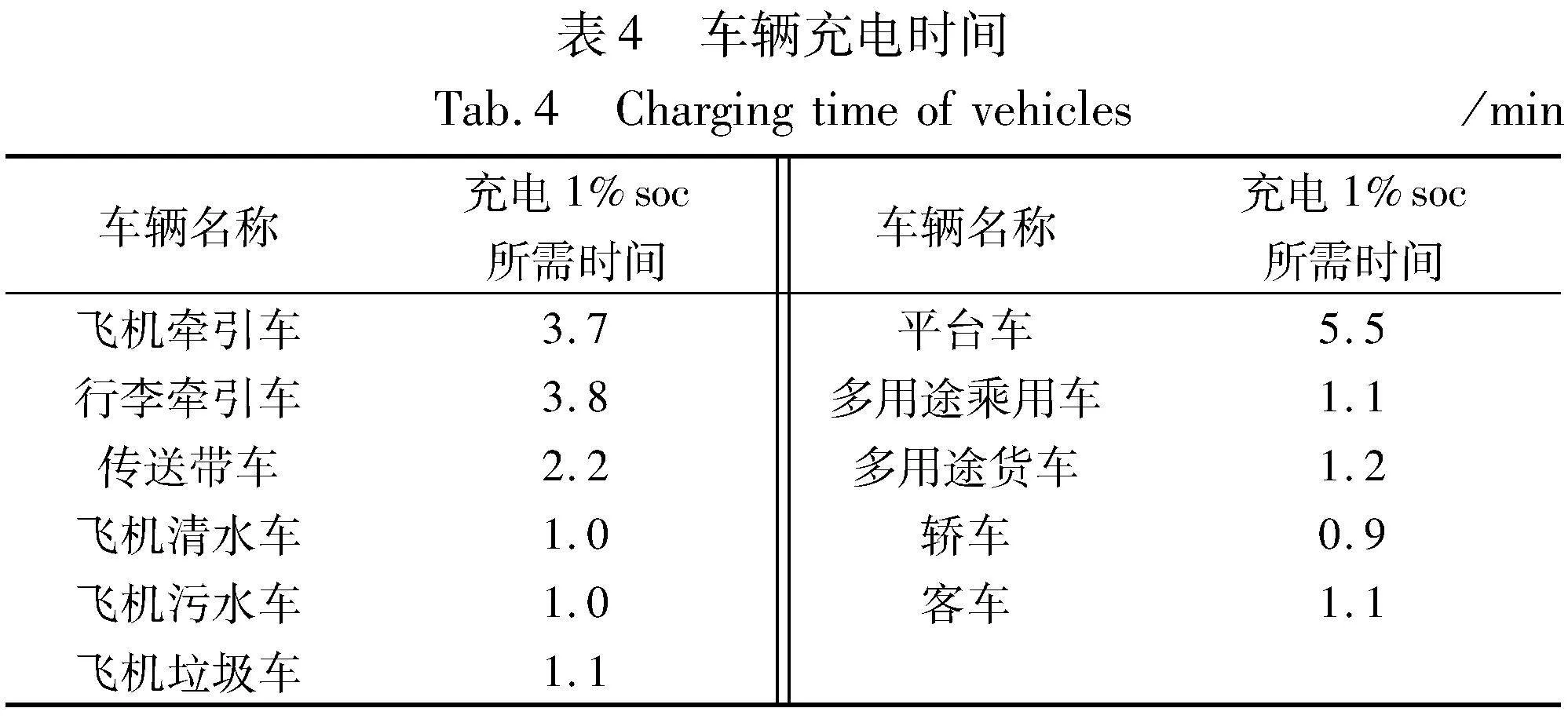
车辆对航班进行完保障服务后，有充电需求的特种车辆由于车辆种类不同，充电速率会产生相应的差别，对该机场2021年7月1日～2021年9月30日的车辆充电数据进行计算，得到不同车辆充电1%soc所需的时间，如表4所示。

4.2 航班保障车辆调度结果

通过输入该机场在2021年9月1日中384个航班离港数据，得到11种特种车辆的保障策略以及共计496次特种车辆的充电请求。在得到的所有车辆充电请求数据中选取的部分数据如表5所示。之后特种车辆都是在此数据基础上进行充电调度，根据车辆充电前保障最后一个航班所在的机位位置，在与其最近的几个分区中，由设定的车辆充电调度算法计算出车辆前往的目标充电桩。

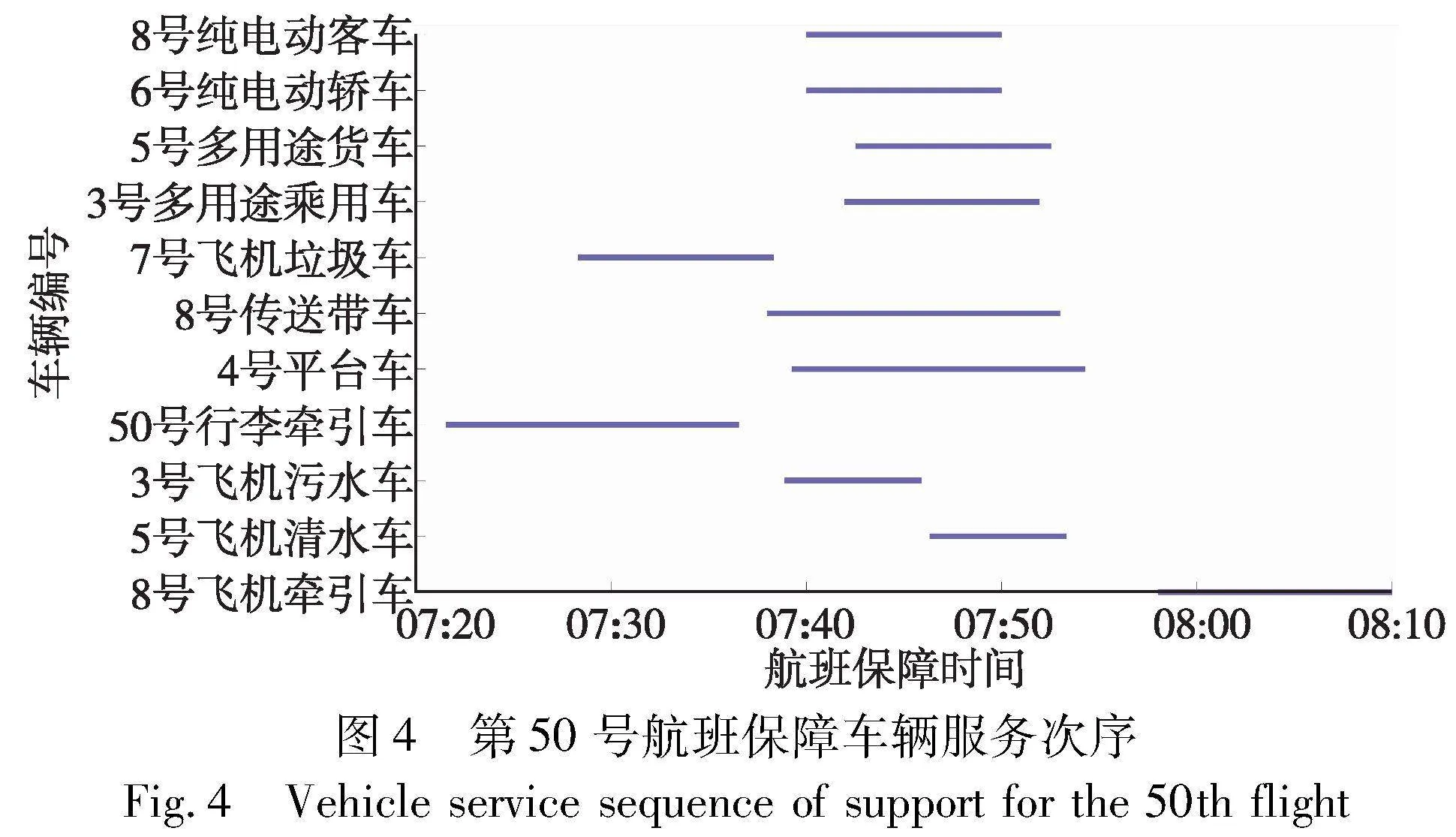
从所有航班中选取了一个第50号航班的各特种车辆的调度策略，其车辆保障服务次序如图4所示。由图可知：8号飞机牵引车在7：59对航班进行保障，服务到8：10结束；5号飞机清水车在7：46对航班进行保障，服务到7：53结束；3号飞机污水车在7：38对航班进行保障，服务到7：45结束；50号行李牵引车在7：21对航班进行保障，服务到7：36结束；4号平台车在7：39对航班进行保障，服务到7：54结束；8号传送带车在7：38对航班进行保障，服务到7：53结束；7号飞机垃圾车在7：28对航班进行保障，服务到7：38结束。由此可以得出不同特种车辆对航班的先后服务顺序，并满足规定的地面保障服务要求。

在11种特种车辆中选取了一个平台车的保障航班顺序图，如图5所示。由图可知：1号平台车在23：28对第一个航班完成了服务，并在23：32开始对第二个航班进行服务，服务到23：47结束，在23：49对第三个航班进行服务，服务到0：04结束。此时，该车辆若对下一个航班进行服务，其电池容量会小于30%，因此， 0：04为该车辆的预计充电时刻，后续车辆充电调度在此时刻进行。

4.3 车辆充电调度结果

本文对得到的车辆充电请求数据进行充电调度仿真，并采用IAMPSO算法进行模型求解，相关参数设置为：学习因子c1=c2=1.5，最大惯性权重ωmax=0.9，最小惯性权重ωmin=0.18，最大变异因子pmax=0.85，最小变异因子pmin=0.45，学习因子变化系数m=6。就近充电规则为，在车辆充电前保障的最后一个航班所在机位对应的距离最短的几个充电桩中，选择充电等待时间最短的充电桩进行充电。

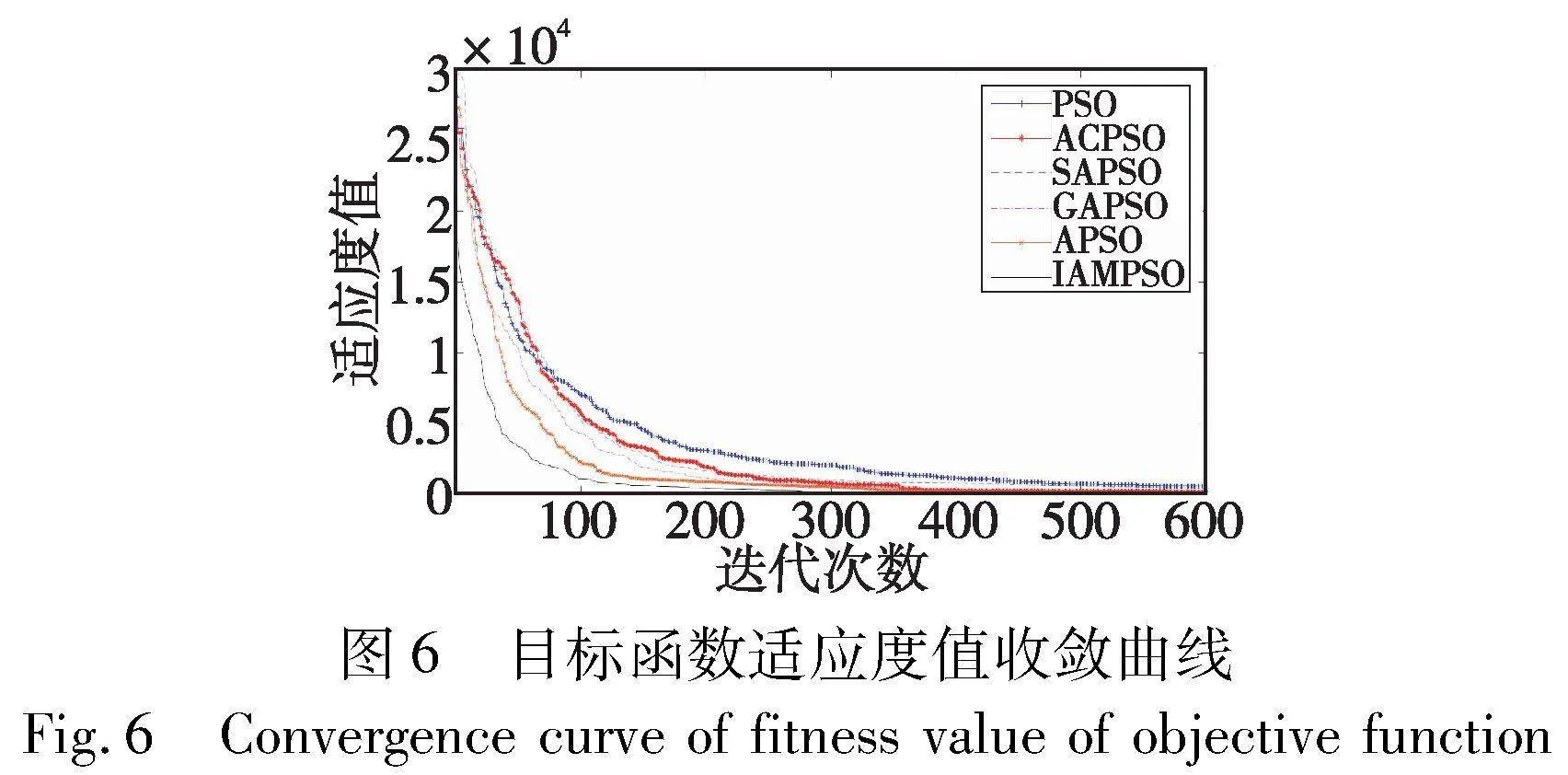
由于本文需要求解模型的变量维数过高，用单独的其他智能优化算法求解精度过低，所以本文将粒子群算法分别和蚁群算法［23］、模拟退火算法［24］、遗传算法［25］进行融合，建立了蚁群粒子群融合算法（ACPSO）、模拟退火粒子群融合算法（SAPSO）以及遗传粒子群融合算法（GAPSO），使这些算法继承了粒子群算法对高纬度变量求解精度高的优点。于是本文求解车辆充电调度模型时用IAMPSO算法与这些改进的粒子群融合算法，以及普通的粒子群算法（PSO）和自适应粒子群算法（APSO）分别进行了对比实验。得到多种改进PSO和IAMPSO算法对目标函数适应度值的收敛情况，如图6所示。从图中可以看到，IAMPSO算法相比其他改进PSO算法有更快的收敛速度，收敛速度越快，就越能在较少的迭代次数以更高的求解精度收敛到目标函数的最优值。对本文来说，对比于其他优化算法，使用IAMPSO算法求解车辆充电调度模型时，在有限的时间内便能得到满足目标函数要求的更优调度结果，避免了因高迭代次数而产生冗长求解时间的现象。

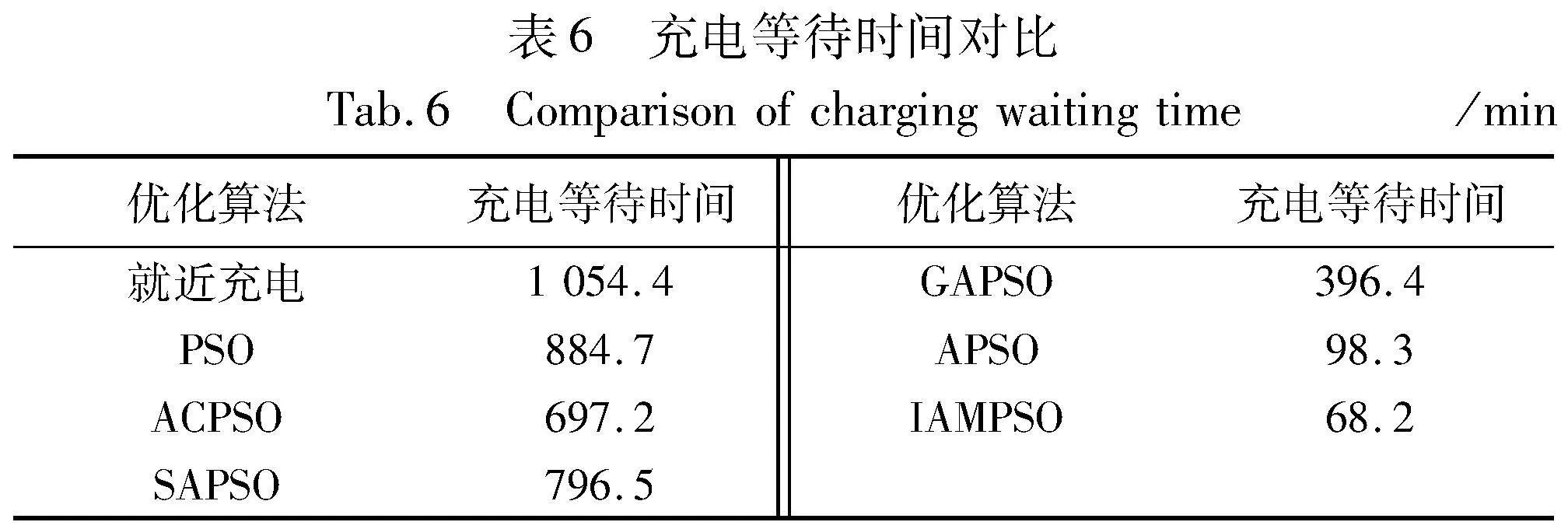
优化前后得到的车辆充电等待时间对比如表6所示。从表中可以看到，相比于就近充电，采用IAMPSO算法后，车辆充电时的排队等待时间降低了93.5%，优化效果远高于其他改进PSO算法，避免了车辆的集中充电现象，车辆充电效率得到了有效提升。

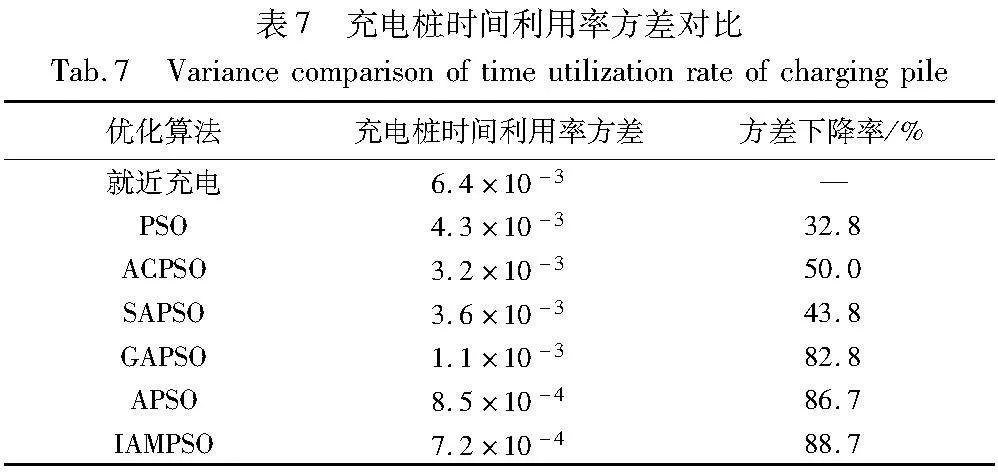
优化前后飞行区充电桩时间利用率方差对比如表7所示。可以看出，采用IAMPSO算法对于就近充电的方差下降率要优于其他PSO算法，全飞行区的整体方差下降了88.7%，方差下降率高于其他算法，说明该飞行区充电桩的利用情况分布得更加均衡，避免了个别充电桩的极端使用，达到了预设的目标函数要求。

5 结束语

新能源车辆在飞行区的大规模运行是未来必然的发展趋势，目前普遍采用的基于就近充电原则的无序充电现象会使机场飞行区的充电桩处于不平衡的使用状态，个别充电桩的极端使用会增加其维护成本及使用寿命，而某些闲置的充电桩又会造成资源浪费，不利于机场配电网的稳定性。同时，在航班高峰段的车辆集中充电现象会产生大量的充电等待时间，会极大影响车辆充电效率。为解决该问题，本文建立了两阶段多特种车辆协同充电调度模型，使用改进的自适应变异粒子群算法进行模型求解，并与国内某枢纽机场的航班数据和车辆充电数据进行对比实验，最终使车辆充电时的等待时间降低了93.5%、飞行区充电桩时间利用率的整体方差下降了88.7%，达到了提升车辆充电效率以及均衡使用充电桩的目标。未来研究会继续针对新能源车辆充电调度策略，在能够满足航班服务标准下，更有效地提高车辆服务效率。

参考文献：

［1］胡振刚， 黄文龙， 张毅. 基于智慧民航视角的民航高质量发展路径探究［J］. 民航管理， 2023（4）： 13-16. （Hu Zhengang， Huang Wenlong， Zhang Yi. Exploring high-quality development path of civil aviation from the perspective of smart civil aviation［J］. Civil Aviation Management， 2023（4）： 13-16.）

［2］Chen Yuxiu， Yu Jian， Li Linlin， et al. An empirical study of the impact of the air transportation industry energy conservation and emission reduction projects on the local economy in China［J］. International Journal of Environmental Research and Public Health， 2018，15（4）： 812.

［3］熊羚利. 面向“双碳”目标的民航绿色发展浅论［J］. 民航管理， 2022（5）： 16-20. （Xiong Lingli. An overview of the green development of civil aviation oriented at carbon peaking and carbon neutrality goals［J］. Civil Aviation Management， 2022（5）： 16-20.）

［4］Szumska E M， Jurecki R S. Parameters influencing on electric vehicle range［J］. Energies， 2021， 14（16）： 4821.

［5］Broihan J， Nozinski I， Poech N， et al. Designing dynamic inductive charging infrastructures for airport aprons with multiple vehicle types［J］. Energies， 2022，15（11）： 4085.

［6］Alam M R， Guo Zhaomiao. Co-optimization of charging scheduling and platooning for long-haul electric freight vehicles［J］. Transportation Research Part C：Emerging Technologies， 2023， 147：104009.

［7］Liu Dunnan， Zhang Tingting， Wang Weiye， et al. Two-stage physical economic adjustable capacity evaluation model of electric vehicles for peak shaving and valley filling auxiliary services［J］. Sustainability， 2021， 13（15）： 8153.

［8］Mei Panpan， Wu Lianghong， Zhang Hongqiang， et al. A hybrid multi-objective crisscross optimization for dynamic economic/emission dispatch considering plug-in electric vehicles penetration［J］. Energies， 2019，12（20）： 3847.

［9］张潇， 栗然， 马涛， 等. 基于主从博弈和贪心策略的含电动汽车主动配电网优化调度［J］. 电力自动化设备， 2020， 40（4）： 103-110. （Zhang Xiao， Li Ran， Ma Tao， et al. Stackelberg game and greedy strategy based optimal dispatch of active distribution network with electric vehicles［J］. Electric Power Automation Equipment， 2020， 40（4）： 103-110.）

［10］Pelletier S， Jabali O， Laporte G. Charge scheduling for electric freight vehicles［J］. Transportation Research Part B： Methodological， 2018，115： 246-269.

［11］Stephen A， Zhou Chenhao， Chew E P， et al. Q-learning based automated guided vehicles recharging scheduling in container terminal［C］//Proc of IIE Annual Conference. 2020： 215-220.

［12］Zhou Kaile， Cheng Lexin， Wen Lulu， et al. A coordinated charging scheduling method for electric vehicles considering different charging demands［J］. Energy， 2020， 213： 118882.

［13］Liu Yonghong， Wu Jianjun， Tang Jie， et al. Scheduling optimisation of multi-type special vehicles in an airport［J］. Transportmetrica B： Transport Dynamics， 2022，10（1）： 954-970.

［14］Zhu Shurui， Sun Huijun， Guo Xin. Cooperative scheduling optimization for ground-handling vehicles by considering flights’ uncertainty［J］. Computers & Industrial Engineering， 2022，169： 108092.

［15］Zhou Jianan， Wu Yaoxin， Cao Zhiguang， et al. Learning large neighborhood search for vehicle routing in airport ground handling［J］. IEEE Trans on Knowledge and Data Engineering， 2023，35（9）： 9769-9782.

［16］Guo Zekun， Lai Chunsing， Luk P， et al. Techno-economic assessment of wireless charging systems for airport electric shuttle buses［J］. Journal of Energy Storage， 2023， 64： 107123.

［17］Barco J， Guerra A， Munoz L， et al. Optimal routing and scheduling of charge for electric vehicles： a case study［J］. Mathematical Problems in Engineering， 2017， 2017： 1-16.

［18］Helber S， Broihan J， Jang Y J， et al. Location planning for dynamic wireless charging systems for electric airport passenger buses［J］. Energies， 2018，11（2）： 258.

［19］Zhang Jichao， Chong Xiaolei， Wei Yazhi， et al. Optimization of apron support vehicle operation scheduling based on multi-layer co-ding genetic algorithm［J］. Applied Sciences， 2022，12（10）： 5279.

［20］Zheng Qingshuai， Gu Yujiong， Liu Yuhang， et al. Chaotic particle swarm algorithm-based optimal scheduling of integrated energy systems［J］. Electric Power Systems Research， 2023， 216： 108979.

［21］Chen Jiumei， Shi Jing. A multi-compartment vehicle routing problem with time windows for urban distribution—a comparison study on particle swarm optimization algorithms［J］. Computers & Industrial Engineering， 2019， 133： 95-106.

［22］Kong Fanrong， Jiang Jianhui， Huang Yan. An adaptive multi-swarm competition particle swarm optimizer for large-scale optimization［J］. Mathematics， 2019，7（6）： 521.

［23］Dong Gaifang，Fu Xueliang，Li Honghui，et al. Cooperative ant colony genetic algorithm based on spark［J］. Computers & Electrical Engineering， 2017， 60： 66-75.

［24］Fang Longjie， Zuo Haoyi， Pang Lin， et al. Image reconstruction through thin scattering media by simulated annealing algorithm［J］. Optics and Lasers in Engineering， 2018，106： 105-110.

［25］Yan Xuesong， Liu Hanmin， Zhu Zhixin， et al. Hybrid genetic algorithm for engineering design problems［J］. Cluster Computing， 2017，20： 263-275.