量子计算技术在金融领域的应用探索

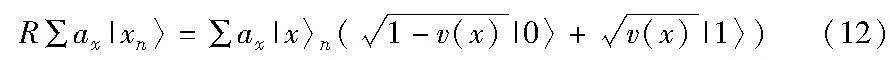
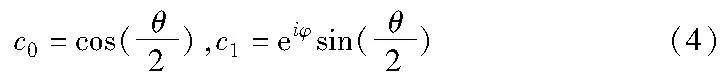
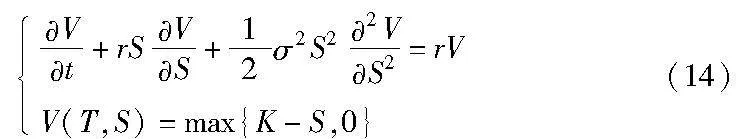
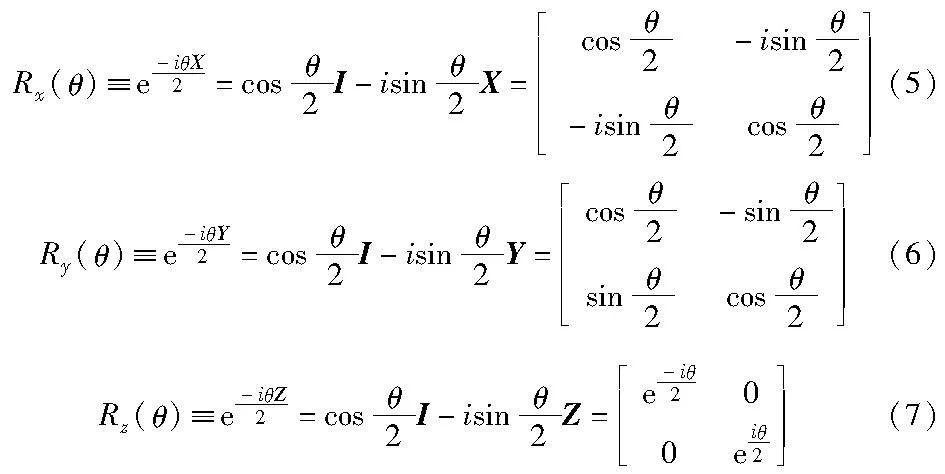
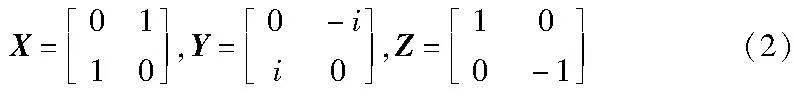
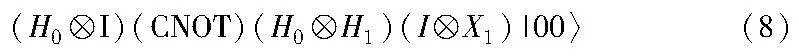
摘 要：量子计算是一种遵循量子力学规律调控量子信息单元进行计算的新型计算机制，被认为在特定算法上可实现并行处理能力，对信息领域技术变革有着重要意义。针对近年来量子计算在金融领域应用进展进行梳理总结。首先，从量子计算基本原理出发阐述了量子比特、量子逻辑门、量子线路等基础理论，重点分析了实现量子计算几种技术路线优缺点；其次，归纳总结了量子计算在衍生品定价、投资组合优化、风险计量、欺诈检测和市场预测方面算法研究进展，以及量子金融软件开发的主要组成架构；最后，分析了目前量子计算技术在金融领域应用发展的三大挑战，即人才问题、效率问题、合规性问题，并对未来发展趋势进行展望，为相关领域研究提供参考。

关键词：量子计算； 量子金融产业； 量子金融算法； 量子金融软件

中图分类号：O455.3 文献标志码：A 文章编号：1001-3695（2024）07-001-1921-09

doi：10.19734/j.issn.1001-3695.2023.11.0529

Application exploration of quantum computing technology in financial field

Abstract：Quantum computing is a new computing mechanism that follows the laws of quantum mechanics to control information units for calculations. It is believed to be able to achieve parallel processing capabilities on specific algorithms and has a great significance for the technological revolution in the information field. This paper summarized the progress of quantum computing applications in the financial field in recent years. Firstly， from the basic principles， it analyzed basic theories of qubits， quantum logic gates， quantum circuits， with a focus on analyzing the advantages and disadvantages of several technical routes for quantum hardware. Secondly， it summarized the research progress of quantum algorithms in derivative pricing， portfolio optimization， risk measurement， fraud detection， and market prediction， as well as the main components and architectures of quantum finance software. Finally， it discussed the talent， efficiency， and compliance challenges in the application and development of quantum computing in the financial field， as well as the prospects for future development trends.

Key words：quantum computing; finance industry; quantum financial algorithm; quantum financial software

0 引言

量子计算在特定算法上具有并行处理能力，在解决金融领域中复杂的和计算密集型的问题等方面相对于经典计算机具备显著优势，甚至可能改变金融业务及其安全风控的底层逻辑，因而得到世界各国的高度关注。国内多家知名高校、科研院所和科技创新企业争相在量子计算领域投入巨额研发经费并取得了一定原创性成果，光量子计算机“九章”［1］和超导量子计算机“祖冲之号”［2］“悟空”等相继问世。这一系列科技突破也加快了国内各大科研机构对量子算法在多领域的应用研究，引起了量子计算机研发实体与银行等金融机构、高校院所对量子金融算法展开合作研究的热潮。2020年9月超导量子计算公司本源量子与中国建设银行旗下建信金科合作成立量子金融联合实验室。本源量子随后推出了量子期权定价算法和量子在险价值（value at risk，VaR）估计算法，其后又开发了量子最大相关最小冗余（maximum relevance and minimum redundancy，MRMR）算法，并推出了量子金融衍生品定价库。中国建设银行推出了量子贝叶斯网络算法和量子投资组合优化算法这两项量子金融应用算法［3，4］。2022年3月北京量子信息科学研究院与光大科技、玻色量子联合发布了量子计算投资组合策略平台。2022年12月玻色量子与平安银行也达成了研究推动传统算法转换为量子算法的合作协议。2023年8月，超导量子计算企业量旋科技与平安银行共建“量子信息+金融科技”平台并推出了用于银行智慧运营的量子聚类算法［5］，双方将在量子金融算法开发、软件开发等方面展开紧密合作。

国外的量子计算研发机构与金融机构在量子金融算法研究方向的发展十分迅速，研究的算法涵盖金融领域的多个问题，科研机构与金融机构的合作也愈发紧密。布局超导量子计算的IBM与美国银行、高盛在内的近十家大型银行和投资机构在量子金融算法领域开展了合作［6］；初创公司D-wave和西班牙CaixaBank、万事达等合作开发量子混合应用程序［7］，加快复杂问题求解；汇丰银行与Quantinuum正合作探究量子机器学习和量子自然语言处理对银行业务的潜在好处［8］；美国最大商业银行摩根大通与QC ware和巴黎大学联合开发了量子计算算法，改进深度对冲模型，并开发用于最优化理论和密码学的量子算法［9］；Zapata Computing公司设计了多种量子经典混合算法为资产定价、投资组合优化和资产配置提供解决方案［10］；量子安全加密公司Arqit开发了提供量子安全的数字金融工具［11］，目前已被融资解决方案公司Traxpay所使用；2023年初，Multiverse Computing、Pasqal也携手法国东方汇理银行验证了量子启发算法在估值和信用风险评估方面的价值［12］。

当前，虽然金融市场中的数学分析模型和算法技术取得了长足的进步，但经典算法的局限性已经慢慢显现，亟需新的计算方法满足金融机构低延时、大数据、高精度的计算任务需求。因此，近年来产业界和学术界对探索量子计算解决经典金融问题产生了浓厚的兴趣，一系列量子金融理论和算法被提出，量子金融算法的优越性逐渐被产业界和学术界所认可。

1 量子计算基本原理

1.1 量子计算与量子比特

量子计算是一种按照量子力学规律调控量子信息单元进行计算的新型计算体制。由美国阿贡国家实验室的Benioff［13］首先于1980年提出了量子计算的概念；1982年，物理学家Feynman［14］提出了使用量子体系实现通用计算的方法；1994年，贝尔实验室的Shor［15］证明了量子计算机能够进行大数因子分解的运算，并且运算速度以指数倍优于经典计算机。量子计算被认为是能够继续提升计算能力的全新技术途径，将对信息安全产生重大影响［16］。

经典计算机的理论模型是通用图灵机，即以二进制比特0或1为最小单元，由计算机指令进行定义，使系统内部元件的状态根据操作进行跳转，从而达到逻辑运算的目的。五十多年来，经典计算机算力增长一直牢牢遵循着“摩尔定律”［17］：芯片的集成度每18个月增加一倍，计算机算力也随之翻倍。然而，随着硅基芯片上晶体管尺寸逐步逼近纳米级的物理极限，硅基芯片在算力、数据传输和存储中的发展即将面临瓶颈。即使“摩尔定律”仍可能继续有效，传统算力的发展也越来越难以满足现今数字经济时代各行业在数据膨胀背景下对算力的增速需求。

面对“后摩尔时代”的算力危机挑战，如何提升单点计算性能与高效利用算力系统已经成为迎接新一轮产业革命的一项重要课题。在各类算力相关的技术中，量子计算以其兼具更高运算速度和更低功耗的潜质而得到越来越多国家和研究机构的关注，被视为下一个算力时代的星辰大海。量子计算机的理论模型是使用量子力学规律重新定义的图灵通用机［18］，其最小单元通常为二能级体系下的量子比特（qubit）。通过量子计算机定义的操作集合，使不同的量子比特之间通过物理相互作用所产生的系统动力学演化来定义量子态的跳转，两种比特的对比如表1所示。

量子比特的特殊之处在于：其不仅可以表示0或1，并且可以表示同时含有0和1的成分的叠加状态，即

Φ=α|0〉+β|1〉（1）

基于量子力学的态叠加原理，式（1）中α和β均为复数且|α|2+|β|2=1。根据海森堡不确定性原理，粒子的位置与动量不可同时被确定，位置的不确定性越小，则动量的不确定性越大，反之亦然。观测所引起的物理作用，会使得该叠加态会塌缩到与观测行为有关的一组确定状态，经过多次观测可以确定0的概率是|α|2，1的概率是|β|2。这样在处理量子比特时可以同时对0和1进行并行操作，加快运算速度，并且n个量子比特可以保存2n个状态，使得量子计算机能够在计算效率和存储空间上指数倍优于经典计算机。

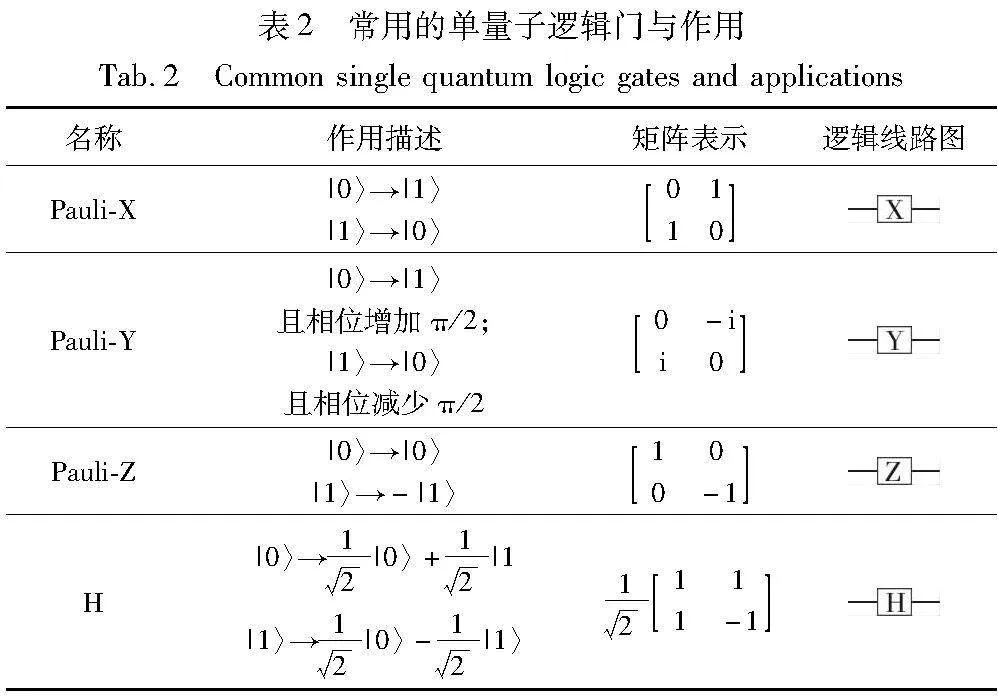
量子比特的运行由量子逻辑门来控制。单量子逻辑门是对单个量子比特操控的逻辑门，且满足可逆运行性。已知非门和单位门是最简单的单量子逻辑门，其他一些常用的单量子逻辑门如下：

易证这三个矩阵均为酉矩阵，它们被称作Pauli矩阵，被广泛应用在量子力学和量子计算科学中。还有几个很重要的单量子逻辑门：

这些单量子逻辑门作用于单个量子比特会改变单量子比特状态，从而可以通过量子比特状态的改变来处理信息，达到逻辑运算的目的。

表2展示了常用的4个单量子逻辑门与对量子比特的作用效果。更进一步，一个单量子比特处于状态c0|〉+c1|1〉可表示为由参数（θ，φ）所确定的布洛赫球面上的一个c1，可表示为

因此，所有单量子逻辑门对单量子比特的操作均可看作是将block球面的点绕某一坐标轴进行的旋转操作，定义x、y和z轴的旋转门分别如式（5）～（7）所示。

以上公式均由欧拉公式推导所得，它们分别表示将单量子比特绕x、y和z轴旋转θ角所对应的操作。

1.2 多量子逻辑门

多量子逻辑门用来操控多个量子比特的叠加态，可以是交换门，也可以是利用一到两个量子比特作为控制位对其他量子比特进行操控的受控门，常用的多量子逻辑门如表3所示。

多量子逻辑门所对应的矩阵也均为酉矩阵。在希尔伯特空间中存在无数个酉矩阵，不可能将每一个酉矩阵都对应一个量子逻辑门，因此定义一组量子逻辑门可以无限近似于任意的酉矩阵，这组量子逻辑门可以称为通用量子门［18］。

Toffoli门对于经典线路模型而言是通用的，因此经典线路模型包含于量子线路模型中。经过数学推导证明，单量子逻辑门和受控非门的集合可以组成通用量子逻辑门，它们的组合可以近似为任意酉变换。但这并不表示将任意酉变换转换为通用量子逻辑门的排列组合是一个简单问题，它具有指数级的运算复杂度。目前，尚未发现可以在多项式时间内使用通用量子逻辑门制备任意量子逻辑状态的通用算法。

1.3 量子线路模型

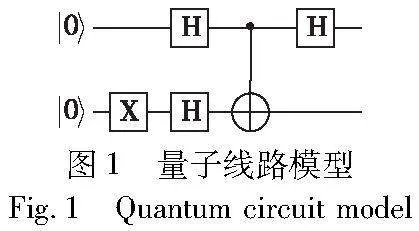
同经典计算科学中的线路模型类似，量子线路模型可以用来更好地诠释量子算法的运行过程。其他的计算模型对同一量子计算问题的资源需求也基本相同，这里不再赘述。利用1.2节介绍的通用量子门的排列组合可以对量子比特进行任意酉变换，而量子线路模型就是通过多种酉变换的组合实现量子算法的过程。例如图1的量子线路模型中表示初始两个量子比特的状态为|00〉，经过一系列量子门操作后的表达式为H0（CNOT）H0H1X1|00〉。

其中，该线路下标表示作用在0位或1位上的量子逻辑门，将上述表达式张量乘到同样的空间大小并作用于|00〉，则该量子线路对应的计算过程与结果为

经过量子逻辑门操控后，对式（8）终态量子比特进行测量，有50%的概率得到|10〉态，有50%概率得到|11〉态。

有时候量子线路中会出现一些经典线路中不常见的概念。首先，经典线路会出现连线汇合，例如逻辑与门和逻辑或门，易证该操作是不可逆的，所以也是非酉的，因此在量子线路中禁止出现连线汇合。由于量子的不可克隆性［19］，从一个比特产生多个拷贝在量子线路中也是禁止的。另外，量子线路中禁止出现回路，即从线路的一部分到另一部分的反馈。量子线路是量子算法的一种逻辑表达，是量子算法运行的过程控制。

1.4 量子计算机硬件实现

2000年，IBM的物理学家DiVincenzo［20］提出了实现可扩展通用量子计算硬件系统必须满足的几个必要条件，后来成为了量子计算领域广为人知的“DiVincenzo标准”：a）可扩展的、性能良好的量子比特；b）能够对量子比特进行初始化；c）量子比特的退相干时间要足够长；d）能够实现普适的量子门逻辑操作；e）对量子比特状态能够精确测量。根据“DiVincenzo标准”，当前实现量子计算的物理方案纷繁复杂，其中发展迅速且极具潜力的方案归纳起来主要有超导量子计算［21～23］、核磁共振量子计算［24～26］、囚禁离子阱量子计算［27～29］、光量子计算［30～32］、拓扑量子计算［33～35］等，如图2所示。将实现量子计算各实现途径的优缺点汇总如下：

a）超导量子计算方案。采用宏观超导量子器件（人造原子），具有设计灵活、较易控制和读取、可通过微纳加工技术制备集成、可扩展性良好等优点；但缺点是需要极低温环境，并且对磁场、宇宙射线等的干扰比较敏感。

b）硅基量子计算方案［36］。采用半导体芯片上的自旋体系，具有半导体工艺、可大规模集成、相干时间长、芯片化等优势；但缺点是芯片加工难度高、调控难度高、当前可控的比特数量较少。

c）核磁共振量子计算方案。利用特定分子的原子核自旋编码量子比特，具有操控精度高、体系相干时间长、易于演示量子算法等优点；但缺点是受限于单个分子的可控核自旋数量，体系难以大规模扩展。

d）囚禁离子阱量子计算方案。采用自然离子，具有很好的比特全同性、操控精度、以及超长的相干时间等优点；但缺点是大规模扩展仍有一定难度，未来有望通过芯片化的离子阱方案克服。

e）光量子计算方案。采用光量子体系，在室温大气环境下具有抗退相干、单比特操纵简单精确、可提供分布式量子计算的接口等优势；但缺点是光子之间耦合比较困难，且光子本身容易被线路损耗，不利于大规模集成。

f）中性原子量子计算方案［37］。采用光晶格中的中性原子阵列，具有体系纯净、比特全同、可阵列化等优点；但缺点是调控难度高，且存在原子丢失的问题。

g）拓扑量子计算方案。利用的是人工固体系统的马拉约纳模式，具有拓扑保护、操控鲁棒、芯片化等优点；但缺点是该方案还处于早期阶段，需要验证基本的马拉约纳比特以及其基本操作。

在众多技术路线中，超导量子计算由于同经典集成电路工艺相融合，是最近几年发展最为迅猛的技术路线。超导量子芯片的核心技术是量子比特电路的设计、加工和制造。随着材料、工艺、设计的改进，量子比特的形态从最初的电荷、磁通和相位量子比特构型发展到二维平面Transmon、平面Xmon和表面码等复合构型的量子比特［38］，未来将会发展出基于更加复杂的三维量子比特，可调量子比特数目将大为拓展。2022年11月，美国IBM公司发布433比特超导量子计算机量子处理器“鱼鹰”，将量子比特集成数量提升到百量级，标志着量子计算技术发展进入下一个中等规模阶段。

1.5 量子计算的并行优越性

以上几节展示了量子计算的物理学原理、计算逻辑与物理硬件实现方法。以上的物理硬件实现方法中除了实现式（1）所体现的单个量子比特的叠加态，还会实现量子比特之间的纠缠态，如式（8）中两个量子比特的纠缠态。量子计算天然存在的比特叠加与纠缠状态，使得大量信息可以同时分布在由N个比特组成的2n个量子态上并行处理，从而实现指数级加速。相比于量子计算，经典计算机的并行计算则需要对数据进行分布式存储，需要大量经典比特存储信息，消耗大量内存，针对复杂高维问题容易遇到内存瓶颈，且经典计算机的指令级并行性有限。因此在处理经典计算机需要指数级时间的问题时，量子计算机具有一定的优越性［39］。

2 量子金融算法

2.1 经典金融计算的痛点

金融领域有着广泛的计算需求，许多业务涉及大规模数据处理、高度复杂的计算和难以解决的组合优化问题，比如，量化金融投资领域中常用到经典蒙特卡罗模拟来解决衍生品定价、风险评估等［42］。利用蒙特卡罗模拟资产价格的未来演化时，需要生成大量的随机路径，生成这些路径需要进行复杂的数学计算和随机抽样；除此之外，处理高维问题时，如多维随机过程的模拟，问题维度的增加会导致蒙特卡罗模拟算法的计算复杂度呈指数级增长，计算需求急剧增加，导致计算时间显著增长。而且蒙特卡罗模拟通常是计算密集型任务，对计算资源的需求非常大，因此在风险评估和衍生品定价中，经典计算机无法以足够的运行速度处理大规模的模拟，但是量子计算机的存储和并行优势可以加速处理这些密集型任务。

金融领域中的投资组合优化模型、风险管理模型等还会涉及求解大规模的线性方程组，这些金融模型所涉及的线性方程组通常非常庞大且复杂，经典计算机在处理这些大规模线性方程组时可能会面临内存和计算能力的限制，导致计算时间显著增加。比如在投资组合优化问题中，对应的通常是一个经典的带有约束的二次规划问题，最常见的形式是马可维茨（Markowitz）投资组合优化问题［43］，此问题的目标是最小化投资组合的方差，同时满足预期收益率和权重的约束。为求解这个二次规划问题，通常会转换为求解一个与资产规模正相关的大规模线性方程组，其中协方差矩阵规模是资产数量N的平方量级，当协方差矩阵变得非常大时，经典计算求解这样的大规模线性方程组的计算复杂度通常是N的立方。在计算投资组合的风险暴露时，也会涉及到解线性方程组的模型，比如风险平价模型（risk parity model）［44］。这些金融模型都会导致经典计算机求解这样的线性方程组时会遇到内存问题与计算效率问题，而量子计算在这两个方面的优势也有望为解金融领域的大规模线性方程组提供更高效的解决方案。

金融市场的高频交易和订单执行要求快速、实时的决策和优化，这需要算法对市场作出动态预测，以决定在未来一段时间内每个时刻应该采取的最佳交易决策，以最小化总体交易成本。此问题通常可以建模为一个马尔可夫决策过程［45］，并采用动态规划来解决。一种经典的动态规划算法是通过机器学习算法，比如Q学习算法（Q-learning）来求解马尔可夫决策过程［46，47］。在高频交易过程中，市场信息所组成的状态空间可能非常庞大，而Q学习算法需要存储和更新每个状态-动作值，这导致了庞大的状态空间和内存需求，交易决策的复杂性使得经典算法需要在交易空间中进行搜索和优化，计算的复杂性也随之增加。但是，量子计算的高效性和并行性可以使其在快速的交易执行和优化方面具有潜在优势［48］，有助于在瞬息万变的市场中获得更有利的交易结果。

2.2 应用方向

针对上述金融领域中经典计算的痛点，目前，已有一系列量子计算算法的相关理论研究被提出并有望应用于金融产业，包括解决投资组合优化问题的量子近似优化算法（quantum approximate optimization algorithm，QAOA）［49］、求解高阶组合优化问题的变分量子算法［50］、用于计算期权定价期望值的量子幅度算法［51］、用于降维和特征选择的量子主成分分析算法［52］、用于金融领域搜索问题的Grover量子搜索算法［53］。受益于这些相关理论算法，新型量子金融算法方面也有了新的突破，例如可以更有效地分析大规模金融数据、识别模式和趋势的量子机器学习算法［54］，用于随机建模、定价的量子蒙特卡罗算法［55］和量子偏微分方程求解算法［56］，用于投资组合管理、融资、资源分配等问题的量子增强SCP（set cover problem）求解算法［57］、量子增强MIP（mixed-integer programming）求解算法［58］和量子启发式算法等［59，60］。这些新型量子金融算法在理论上均具备金融领域实际应用层面的巨大潜力，并已经被前文所提及的金融机构所认可。

应用于金融服务的量子算法主要集中于以下几个方向：衍生品定价、投资组合优化、风险计量、反欺诈和市场预测，如表4所示。

当不同的量子金融算法应用于这些金融领域的具体方向时，这些算法体现出不同程度的加速优势。这些相对于经典计算机的加速优势来源于量子计算应用于金融算法时的并行和存储的优越性。经典蒙特卡罗算法应用于衍生品定价时遇到了计算效率与存储两个方面的瓶颈，而量子蒙特卡罗方法应用于衍生品定价则有望解决相关痛点［61］，量子计算的并行性可以使得量子蒙特卡罗方法表示多个随机路径，每个路径对应于衍生品价格的一个演化轨迹，同时利用量子计算的并行性，量子蒙特卡罗方法可以同时模拟和评估多个路径，而无须像经典计算那样逐个顺序执行，从而减少总体模拟时间。金融高频交易的市场预测所用到的量子隐马尔克夫模型也是通过量子计算的并行性来实现加速优势［62］，在量子隐马尔克夫模型中，量子态叠加可以表示不同的市场状态，使用量子演化算子描述市场状态的演化过程，通过量子计算的并行性可以在多个时间步骤上同时演化系统状态［62］。量子神经网络结合量子计算的并行特性与神经网络的结构［63，64］，也为高频交易行中的市场预测提供了潜在的解决方法。在量子神经网络中，神经网络的层可以用量子门实现，允许在同一个时间考虑多个输入的影响，通过增加量子神经网络的深度，可充分地利用量子计算的并行性，以更快的速度进行预测和决策。

2.3 算法分析

接下来，针对金融产业中主要的应用方向，对五种未来有望体现更大量子优势的新型量子金融算法进行详述。

1）量子近似优化算法与遗传算法混合的量子单目标组合优化算法

在金融领域投资组合优化问题中，需要解决的关键问题之一是如何在给定的可选资产中选择最优的资产组合大化收益。此类优化问题需要最小化一个二次损失函数F：

基于量子近似优化算法和遗传算法（genetic algorithms，GAS）两类量子算法的混合单目标投资组合优化算法将有望解决此类复杂问题。QAOA算法的核心思路是通过模拟绝热演化的过程来计算一个组合问题的最优解。对于投资组合问题，通过变量替换可以构造出损失函数对应的末态哈密顿量，再取所有满足约束条件状态的均匀叠加态作为初态，从而实现对状态的并行处理，通过构造绝热演化问题对应的Trotter分解数值解的量子门序列得到含参量子线路［77］。通过参数赋值-量子线路运行-测量统计结果-传统优化器参数优化的循环步骤，可以使用较短的量子线路完成投资组合问题最优解的选取。这一过程中QAOA不仅在投资组合的表示上利用了量子计算的并行特性，在最小化目标函数的演化过程中也会通过量子计算并行地演化不同的解，更快速地搜索潜在的最优解。量子测量的并行使得QAOA可以同时获取多个投资组合的适应度。

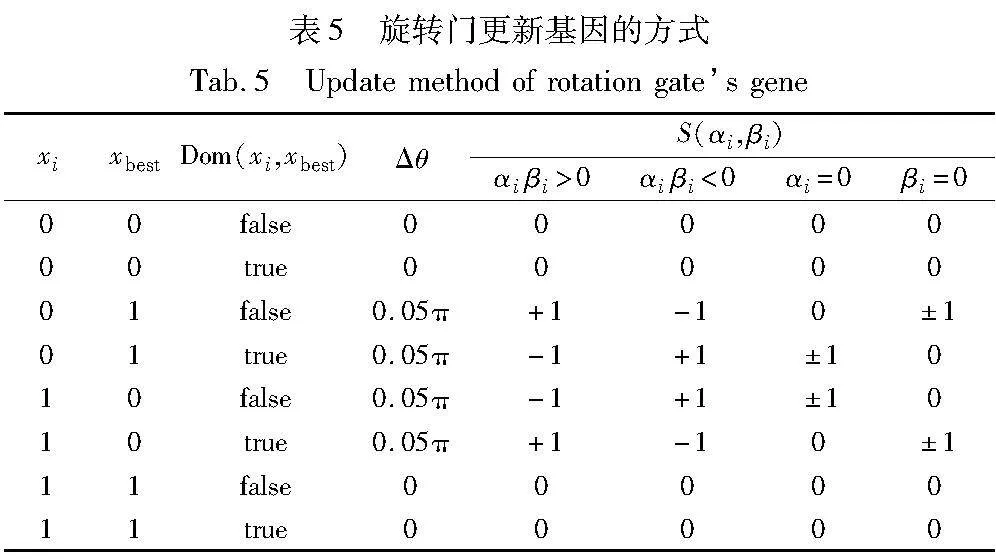
GAS算法的核心思想是将投资组合中寻找最优的资产配置的搜索问题转换为一个量子计算问题，量子计算的并行性可以使得一次测量过程中获取多个资产配置方案的适应度，加速适应度评估过程。GAS算法具有自适应性，可以用于各种类型的搜索问题而无须先验知识，因此常用于优化问题的求解。通过设置验证门槛，将优化问题转换为搜索问题，再重复使用Grover迭代算法提高目标项振幅，增加找到解的概率，从而进一步更新验证门槛，GAS算法可以在O（N）的时间内得到全局最优解，其中N为搜索空间大小。表5中：xi，xbest分别代表个体的第i位基因和最优个体对应位置的基因；αi和βi代表第 i位基因0和1状态对应的振幅；Δθ为量子遗传算法中旋转门的旋转角度，其中每个个体表示一个可能的资产配置方案。

2）基于量子遗传算法的量子启发多目标优化算法

金融领域多目标投资组合优化问题是在最大化收益的同时最小化风险的问题，同时解决多个相互冲突的目标。基于量子遗传算法的量子启发多目标优化算法可以用来求解这类问题。该算法利用量子遗传算法更新基因的方式，通过使用量子比特的振幅表达个体的基因信息，利用量子旋转门操作改变振幅更新个体基因，进而通过测量将振幅基因信息表达为确定的个体信息，从而模拟自然选择和遗传机制的过程，不断演化出优秀的投资组合方案。

另一方面，量子遗传算法可对最大化收益、最小化风险的多目标投资组合问题进行求解。相对于传统遗传算法，基于快速非支配排序的量子多目标遗传算法是通过量子比特的振幅表达个体的基因信息，通过量子旋转门操作改变振幅更新个体基因，进而通过测量将振幅基因信息表达为确定的个体信息。

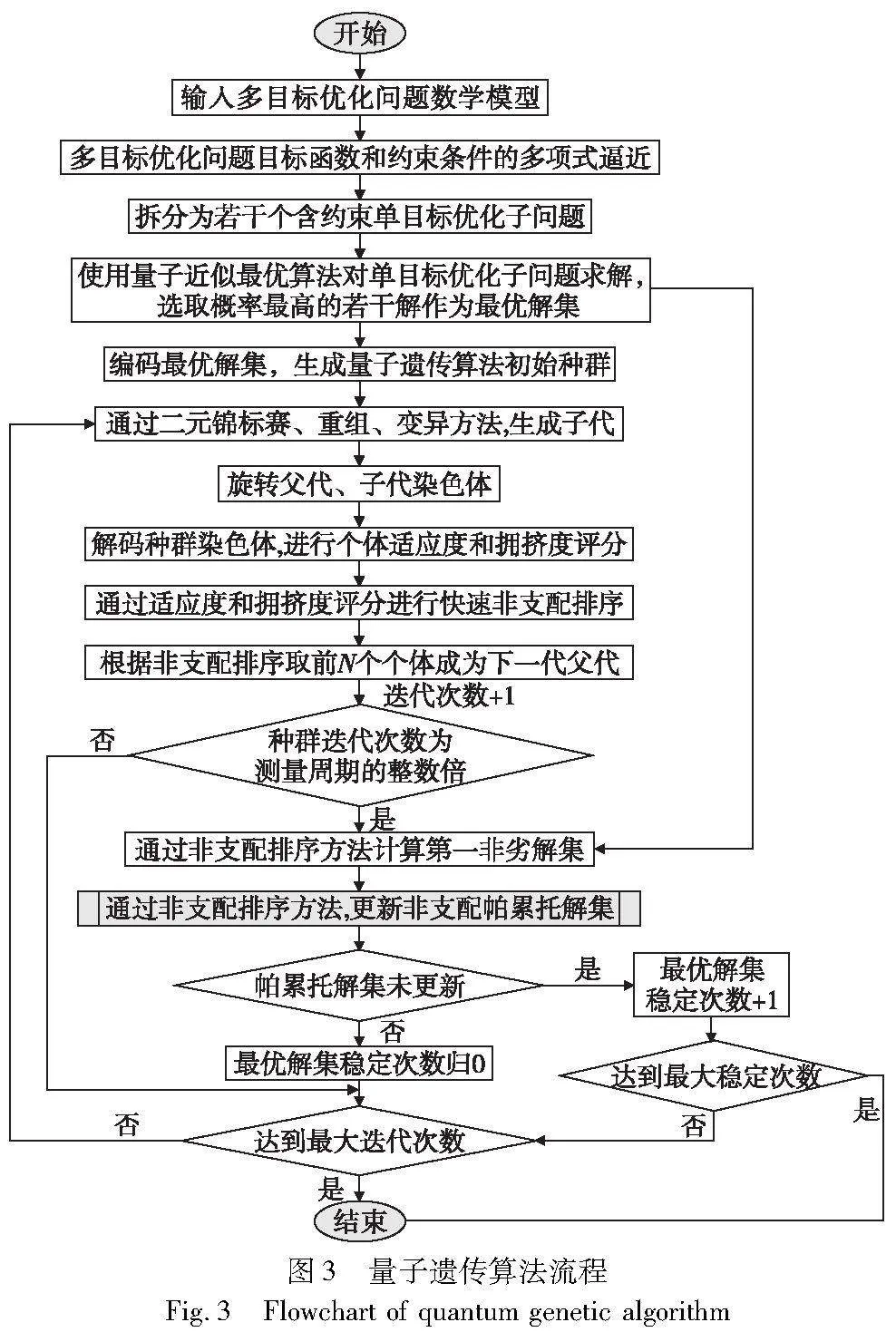
同时，算法引入量子近似优化方法来预先对多目标优化问题的每个单目标子问题进行求解，从而提前锚定理论最优解集中的部分解作为量子遗传算法的初始种群，以加速演化过程。量子遗传算法的具体流程如图3所示。

3）基于量子蒙特卡罗和量子贝叶斯估计的风险价值计量算法

风险价值是衡量金融资产或证券组合在未来特定时期内的最大可能损失的重要工具，它衡量了某一金融资产或证券组合价值在未来特定时期内的最大可能损失。

VaRα（X）=-inf{t|FX（t）≥α}=-inf{t|Pr（x≤t）≥α）}（10）

其中：VaRα（X）表示损失收益变量X的风险价值计量，VaRα（X）=N意味着X以1-α的概率（置信区间）损失不会大于N；

等式后两项就是上面描述的数学表达，FX表示X的分布函数，-inf{t|FX（t）≥α}表示用分布函数找到X的α-分位点；等式最后一项中Pr（x≤t）计算x≤t的概率，找到满足Pr（x≤t）≥α的最小的t（由于X是损失收益分布，t一般是负数），－t即为损失的具体数额。

为了准确计算VaR值，量子计算可提供新的解决方案。如表4所示，量子蒙特卡罗和量子贝叶斯估计方法可对风险进行计量。这两种方法都能通过量子计算加速传统方法VaR计算的复杂度，从平方级加速到至多指数级。具体而言，基于量子蒙特卡罗的方法通过并行随机抽样模拟投资组合收益率的分布，进而计算出VaR值。其核心思想是通过量子振幅估计算法取代传统蒙特卡罗算法，在需要数值模拟的场景中大大减少了分析所需的样本量。对于n量子比特，假设测量结果得到x的概率为|ax|2，记风险价值函数为v（x），量子蒙特卡罗算法首先通过初态制备得到

通过辅助比特和旋转算子得到

由此，通过测量辅助比特得到1的概率，即可得到所需的风险价值：

E［v（A）］=∑|ax|2v（x）（13）

由于量子比特的叠加与纠缠特性，通过量子振幅估计方法，可以用n个比特表示2n种情况从而实现对VaR值计算的平方级量子加速。

而基于量子贝叶斯估计的方法则利用贝叶斯推断对历史数据进行建模，将风险分布的参数作为潜在的估计目标，并对未来风险进行预测。量子贝叶斯估计算法结合了贝叶斯统计学的思想和量子计算的特性［78］，特别利用了量子计算的并行性加速估计潜在的风险分布，其通过量子计算的并行性将估计问题的不同参数编码为量子态中的叠加态，在同一时间就可处理多个可能的参数组合，从而加速风险分布估计。贝叶斯估计的核心是通过观察数据更新概率分布，量子贝叶斯估计可以用试用量子贝叶斯更新算法，从而通过量子叠加态的并行更新概率分布，以适应新的观测数据。

4）基于量子虚时演化的金融衍生品定价分析方法

金融衍生品是具有高杠杆效应和低流动性的金融产品，其定价问题一直是金融领域的痛点和难点。基于量子虚时演化方法，可为金融衍生品定价提供高效的计算方法。该方法可以实现传统偏微分方程期权定价方法的至多指数级量子加速。例如，针对欧式期权定价问题，该可以方法结合Black-Scholes-Merton（BSM）公式，通过量子线路模拟薛定谔方程的演化，得到方程数值解，进而实现对期权定价的指数级加速［79］。以欧式期权为例，通过BSM公式，欧式期权的定价满足偏微分方程［79］：

其中：K为行权价格；r为无风险利率；σ为波动率；T为到期时间，t∈［0，T］。通过定义Black-Scholes哈密顿量H^BS：

结合后验选择技术，通过量子线路模拟此薛定谔方程的演化，可以得到方程数值解，进而对方程的数值求解在空间复杂度上实现至多指数级的量子加速，从而实现对期权定价的指数级加速。同时由于最终得到的结果是期权价格关于标的价格的分布曲线，所以通过简单计算即可得到期权相应的参数。

5）基于量子神经网络的金融欺诈检测模型方法

金融欺诈是一个严重危害金融市场稳定和投资者利益的问题。为了有效检测和防范金融欺诈行为，基于量子神经网络的金融欺诈检测模型可以用于欺诈检测。该模型的核心是通过量子门操作实现传统神经网络的类似功能，利用含参线路构造量子全连接层和量子卷积层［80］。

量子神经网络的构造思路类似于传统神经网络，其核心是通过量子门操作实现传统神经网络的类似功能。通过类似于QAOA的方法，使用含参线路可以构造量子全连接层和量子卷积层，同时通过量子比较器可以构造部分分段多项式激活函数的量子版本。量子神经网络由于量子比特的叠加特性，可以用n个量子比特并行表示传统神经网络2n维的数据。对应地，实现全连接层、卷积层等功能相对于传统神经网络需要的参数更少，可以有效避免模型过拟合问题。由于量子线路所有操作均为酉矩阵，数据向量本身模长不变，所以从线路设计上更不容易出现梯度爆炸或消失。另外，由于最终输出结果为概率分布，相较于传统神经网络的概率输出，不用额外添加softmax层［81］，量子神经网络对概率的表示更为自然，在金融欺诈这类分类问题中更为适用。使用量子神经网络进行金融欺诈检测建模，相对于传统神经网络模型训练参数更少，模型更为稳定，且其概率表示形式更符合欺诈检测的问题需求，从而提升模型的判断准确率和检测速度。

6）量子金融算法评估研究

目前量子金融算法的计算评估主要依赖于数学理论推导，在对算法的计算复杂度分析中基本都假定所有量子比特是全连通的，并且所有单比特和两比特量子门都是可以直接实现的。此类复杂度评估标准相对比较粗糙，不符合目前含噪中等规模量子计算机（noisy intermediate-scale quantum computers，NISQ）时代量子芯片的实际情况，难以给出算法真实可执行时的硬件指标参考［81］。

在理论上对服务于金融的量子算法评估研究主要分为两大类：以量子蒙特卡罗方法、量子贝叶斯估计方法为主的纯量子算法；以QAOA、GAS、量子神经网络为主的变分量子算法。针对这两类算法，当前有两种不同的算法评估维度。对于纯量子算法，基于量子计算机硬件，对算法进行基于真实量子芯片可执行的线路映射拆解，评估算法在量子芯片上运行所需的量子比特数和单比特、两比特基本量子门操作数，给出基于量子计算机硬件的算法线路深度。同时，通过线路深度，结合初态制备保真度和测量保真度，评估量子算法在不同精度计算要求下的单比特、双比特门保真度需求，为纯量子算法在金融市场中的应用给出硬件指标计量标准。对于变分量子线路，目前基于量子-电子混合算力网、调度，在统计计算复杂度的同时，还需额外引入算法在量子线路和传统计算机之间的数据传输时间，给出基于真机的量子-电子混合算法运行时间评估体系。

3 量子金融软件平台

量子计算在金融市场上有巨大的应用价值空间，目前，国内外已有一些先行企业展开了基于量子云平台的金融服务软件研发。为了降低量子金融算法应用门槛，提高量子金融算法迭代效率，加快量子金融算法落地运用，各量子计算研发实体与金融机构建设了量子金融服务软件原型平台，比如IBM结合Qiskit软件中金融模块的云平台IBM composer。本源量子与中国建设银行旗下金融科技公司建信金科合作共建量子金融应用实验室依托其量子云平台完成了期权定价、投资组合优化、VaR值计算、量子贝叶斯网络等量子金融服务样例，并提供了基于图形化界面的线上服务。另外，百度依托其云原生量子计算平台“量易伏”开发了量子期权定价功能，并封装在其QFinance量子金融库中。

总的来说，这些平台旨在通过简单的可视化、模块化线路操作，实现从金融行业应用到底层硬件的整合。这些平台的大致构成可分为应用层、服务层、中间件、硬件支撑和数据存储五个基本层级。

a）应用层。从金融行业中衍生品定价、风险计量、投资组合优化和欺诈检测等实际应用场景出发，分别设计针对不同场景的量子算法，提供市场数据传输功能、分析结果可视化输出功能、应用模型筛选功能、算法参数调整功能，实现高自定义的、模块化的量子算法应用服务。

b）服务层。为了使量子算法更适用于多元化的金融市场环境，同时给软件用户提供便捷的算法优化功能，给量子金融服务系统提供了量子线路编程工具。量子线路编程可提供可视化量子编程工具，实现量子线路的搭建和运行，支持基于基本量子门的图形化编程、代码编程的量子线路图形化展示、量子门序列的模块化整合以及量子算法的模块化调用等功能。同时，服务系统对每次运行的任务进行管理，并且加入了一套基于Web的交互式开发环境。用户可以在线开发和分享包含代码和输出的交互式文档，支持实时代码、数学方程、可视化和markdown等。

c）中间件。量子金融服务系统可通过量子编程语言框架，比如IBM开发的量子编程语言框架OpenQASM［82］、本源量子开发的QPanda等［83］，对量子线路进行基于不同芯片架构的映射，实现量子计算机硬件的服务支撑。同时，在任务调度中基于任务需求和硬件调度情况，提供全振幅、部分振幅、带噪声和张量量子计算模拟器作为量子计算机之外的任务处理接口，旨在解决金融服务高频任务需求和量子硬件性能、数量短缺之间的矛盾。

d）硬件支撑。在硬件上提供基于超导、离子阱等技术路线的量子计算机硬件，基于CPU和GPU的量子模拟器和经典计算机，旨在应对高频任务、量子电子混合任务等各类任务需求。

e）数据存储。提供公共数据存储和个人数据存储。公共数据主要用于存储各类金融市场公开数据，例如A股交易数据、国债数据等，为用户设计金融算法提供参考。个人数据负责存储用户账户密码信息、历史任务数据等私人数据。通过分割和灾备技术，确保信息可用、信息安全。

4 挑战和未来趋势

量子计算在金融领域具有巨大的潜力，但同样面临挑战。一部分挑战来自于量子算法当前的局限性，另一部分则源自于金融领域本身的行业性质。

4.1 量子金融算法的有效执行与人才培养

目前，具备实际应用能力的量子计算机比特规模相对较小且不够稳定，当前的量子算法难以有效地处理具有大规模数据和模型需求的金融问题。其次，金融决策需要高度准确的计算结果，而当前的量子硬件容易受到噪声和误差的干扰，这些噪声和误差可能导致金融算法产生不可接受的结果。此外，现如今量子金融算法的开发和实施需要深厚的量子计算和金融领域知识，掌握相关知识的人才目前仍然相对稀缺。金融专业人士需要学习量子计算的基本原理，而量子专家需要理解金融问题，这需要跨学科的合作。因此，量子计算和金融领域都面临着人才短缺的问题。未来，寻找具备量子计算、金融和计算机科学知识的专业人员来开发和应用量子金融算法也是具有挑战性的难题之一。

人才培养与学科发展是紧密关联的，量子+金融的复合型人才的培养需要有相关交叉学科平台作为土壤。由于量子计算有望为金融领域带来重大的变革，而金融领域本身也为量子计算提供了丰富的研究与应用场景，这有望催生量子金融这一量子计算与金融学的交叉学科新领域。量子金融交叉学科的发展也会推动跨学科的合作，促进金融学家、计算机科学家和量子物理学家之间的合作，为创新提供更丰富的思维和方法，从而促进量子算法在金融领域的进一步应用，加快对量子金融工具和模型的研究，用于解决金融中的特定问题，也更有利于培养掌握金融知识和量子计算技术的交叉学科人才。量子金融交叉学科的发展也可为计算金融学、数理金融学领域的发展开辟新的思路。

4.2 量子金融算法的效率评估

以目前的发展水平，量子计算面临着量子计算硬件制造和维护成本高昂的问题，这使得许多金融机构无法轻易获得量子计算资源，限制了量子金融算法的应用。此外，尽管量子计算具有潜在的优势，但经典计算机在金融领域仍然非常有效。因此，在量子金融算法能够大规模应用之前，需要提供明显的性能优势，展现市场价值，以鼓励金融机构投资于量子技术。另外，随着金融机构对量子计算的兴趣增加，行业还需要建立标准和安全性措施，以确保量子金融算法的可靠性和安全性，包括开发量子金融算法的最佳实践、安全协议以保护敏感金融数据等。鉴于不是所有金融问题都适合使用量子金融算法，一些问题可能仍会在经典计算机上得到更快、更有效的解决方案。因此，对具体问题进行是否可以受益于量子计算的仔细评估仍依然是不可或缺的步骤。

4.3 量子金融算法的合规问题

由于金融机构业务涉及到投资人和一般居民的财产安全，除了上述的技术问题外，金融行业本身受限于合规要求，对新技术的采纳非常慎重。金融机构需要对新技术的风险和回报评估进行逐步积累。因此，量子金融算法可能需要一定的应用推广时间。同时，金融监管机构需要制定新的法规和政策，以适应量子计算和量子通信等新技术，保证量子时代的市场公平性和财产安全。

4.4 量子金融算法发展趋势

目前在金融领域，各大国有商业银行、股份制商业银行、城商行和互联网银行也都开启了数字化转型的工作。随着手机银行、各类支付平台、理财、网贷等数字化金融服务普及，基于安全可靠性的差异化金融服务对计算能力提出了更高要求。量子计算在金融领域资产和风险管理、高频交易、欺诈检测等方面的多项业务中，已表现出非凡的商用潜能。

未来，随着关键技术不断突破，量子科技已逐步从理论和实验阶段开始向实践应用和高速发展阶段转变。未来，随着量子计算机硬件和软件技术的不断进步，量子科技对金融行业进一步赋能，并推动金融科技取得新的突破，推动银行业数字化的进一步发展。

5 结束语

量子计算的天然并行性使得量子金融算法在解决金融问题时具有显著优势，量子金融软件平台的建设将降低使用量子计算解决金融产业实际问题的门槛，量子计算机硬件可通过执行量子金融软件生成的量子线路来获得直观化的结果。尽管量子计算在金融领域的应用还会面临技术和非技术两方面的挑战，但是量子计算在金融产业未来的应用研究一定能迎来无比光明的发展前景。

参考文献：

［1］Zhong Hansen， Wang Hui， Deng Yuhao， et al. Quantum computational advantage using photons［J］. Science， 2020， 370（6523）： 1460-1463.

［2］Gong Ming， Wang Shiyu， Zha Chen， et al. Quantum walks on a programmable two-dimensional 62-qubit superconducting processor［J］. Science， 2021，372（6545）： 948-952.

［3］金磐石. 量子信息技术在金融领域的探索实践［J］. 金融电子化， 2022（2）： 8-10. （Jin Panshi. The exploration and practice of quantum information technology in the financial field［J］. Financial Computerizing， 2022（2）： 8-10.）

［4］陈柄任， 高振涛， 吴磊， 等. 量子近似优化算法在金融量化投资场景中的应用［J］. 银行家， 2023（6）： 100-102. （Chen Bingren， Gao Zhentao， Wu Lei， et al. Application of quantum approximate optimization algorithm in financial quantitative investment scenarios［J］. The Banker， 2023（6）： 100-102.）

［5］吴永飞， 王涛， 王彦博， 等. 量子聚类算法在银行智慧运营场景中的应用［J］. 银行家， 2022（1）： 108-110. （Wu Yongfei， Wang Tao， Wang Yanbo， et al. Application of quantum clustering algorithm in bank intelligent operation scenario［J］. The Banker， 2022（1）： 108-110.）

［6］Chakrabarti S， Krishnakumar R， Mazzola G， et al. A threshold for quantum advantage in derivative pricing［J］. Quantum， 2021，5： 463.

［7］Raymond J， Stevanovic R， Bernoudy W， et al. Hybrid quantum annealing for larger-than-QPU lattice-structured problems［J］. ACM Trans on Quantum Computing， 2023， 4（3）： 1-30.

［8］Lorenz R， Pearson A， Meichanetzidis K， et al. QNLP in practice： running compositional models of meaning on a quantum computer［J］. Journal of Artificial Intelligence Research， 2023， 76： 1305-1342.

［9］Herman D， Googin C， Liu Xiaoyuan， et al. Quantum computing for finance［J］. Nature Reviews Physics， 2023， 5（8）： 450-465.

［10］Coecke B， Spekkens R W. Picturing classical and quantum Bayesian inference［J］. Synthese， 2012，186： 651-696.

［11］Pultarova T. Unleashing quantum into the world［J］. Engineering & Technology， 2019，14（4）： 46-49.

［12］Bermejo P， Orús R. Variational quantum and quantum-inspired clustering［J］. Scientific Reports， 2023， 13（1）： 13284.

［13］Benioff P. The computer as a physical system： a microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines［J］. Journal of Statistical Physics， 1980， 22： 563-591.

［14］Feynman R P. Simulating physics with computers［J］. International Journal of Theoretical Physics，1982，21（6-7）： 467-488.

［15］Shor P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer［J］. SIAM Review， 1999，41（2）： 303-332.

［16］陆军， 张雪松， 栾添， 等. 量子信息系统发展探讨［J］. 中国电子科学研究院学报， 2018，13（5）： 497-501. （Lu Jun， Zhang Xuesong， Luan Tian， et al. The discussion of quantum information system［J］. Journal of China Academy of Electronic Science， 2018，13（5）： 497-501.）

［17］Moore G E. Cramming more components onto integrated circuits［J］. Proceedings of the IEEE， 1998， 86（1）： 82-85.

［18］Nielsen M A， Chuang I L. Quantum computation and quantum information［M］.［S.l.］：Cambridge University Press， 2010.

［19］Wootters W K， Zurek W H. A single quantum cannot be cloned［J］. Nature， 1982，299（5886）： 802-803.

［20］DiVincenzo D P. The physical implementation of quantum computation［J］. Fortschritte der Physik： Progress of Physics， 2000，48（9-11）： 771-783.

［21］Clarke J， Wilhelm F K. Superconducting quantum bits［J］. Nature， 2008， 453（7198）： 1031-1042.

［22］Stancil D D， Byrd G T. Principles of superconducting quantum computers［M］. Hoboken：Wiley， 2022.

［23］Huang Heliang， Wu Dachao， Fan Daojin， et al. Superconducting quantum computing： a review［J］. Science China Information Sciences， 2020， 63： 1-32.

［24］Jones J A， Vedral V， Ekert A， et al. Geometric quantum computation using nuclear magnetic resonance［J］. Nature， 2000， 403（6772）： 869-871.

［25］Jones J A， Mosca M. Implementation of a quantum algorithm on a nuclear magnetic resonance quantum computer［J］. The Journal of Chemical Physics， 1998， 109（5）： 1648-1653.

［26］Xin Tao， Huang Shilin， Lu Sirui， et al. NMRCloudQ： a quantum cloud experience on a nuclear magnetic resonance quantum computer［J］. Science Bulletin， 2018， 63（1）： 17-23.

［27］Kielpinski D， Monroe C， Wineland D J. Architecture for a large-scale ion-trap quantum computer［J］. Nature， 2002，417（6890）： 709-711.

［28］Hffner H， Roos C F， Blatt R. Quantum computing with trapped ions［J］. Physics Reports， 2008， 469（4）： 155-203.

［29］Bruzewicz C D， Chiaverini J， McConnell R， et al. Trapped-ion quantum computing： progress and challenges［J］. Applied Physics Reviews， 2019， 6（2）：021314.

［30］O’brien J L. Optical quantum computing［J］. Science， 2007， 318（5856）： 1567-1570.

［31］Nielsen M A. Optical quantum computation using cluster states［J］. Physical Review Letters， 2004， 93（4）： 040503.

［32］Kok P， Munro W J， Nemoto K， et al. Linear optical quantum computing with photonic qubits［J］. Reviews of Modern Physics， 2007， 79（1）： 135.

［33］Kitaev A Y. Fault-tolerant quantum computation by anyons［J］. Annals of Physics， 2003，303（1）： 2-30.

［34］Nayak C， Simon S H， Stern A， et al. Non-Abelian anyons and topo-logical quantum computation［J］. Reviews of Modern Physics， 2008， 80（3）： 1083.

［35］Stern A， Lindner N H. Topological quantum computation-from basic concepts to first experiments［J］. Science， 2013， 339（6124）： 1179-1184.

［36］Kane B E. A silicon-based nuclear spin quantum computer［J］. Nature， 1998，393（6681）： 133-137.

［37］Graham T M， Song Y， Scott J， et al. Multi-qubit entanglement and algorithms on a neutral-atom quantum computer［J］. Nature， 2022， 604（7906）： 457-462.

［38］Barends R， Kelly J， Megrant A， et al. Superconducting quantum circuits at the surface code threshold for fault tolerance［J］. Nature， 2014， 508（7497）： 500-503.

［39］Harrow A W， Montanaro A. Quantum computational supremacy［J］. Nature， 2017， 549（7671）： 203-209.

［40］Grover L K. A fast quantum mechanical algorithm for database search［C］//Proc of the 28th Annual ACM Symposium on Theory of Computing. New York： ACM Press， 1996： 212-219.

［41］Hales L， Hallgren S. An improved quantum Fourier transform algorithm and applications［C］//Proc of the 41st Annual Symposium on Foundations of Computer Science. Piscataway，NJ：IEEE Press， 2000： 515-525.

［42］Jckel P. Monte Carlo methods in finance［M］. Hoboken：Wiley，2002.

［43］Markowitz H. Portfolio selection［J］. The Journal of Finance， 1952， 7（1）： 77-91.

［44］Roncalli T， Weisang G. Risk parity portfolios with risk factors［J］. Quantitative Finance， 2016， 16（3）： 377-388.

［45］Bellman R. A Markovian decision process［J］. Journal of Mathematics and Mechanics， 1957，6（4）： 679-684.

［46］Ge Yangyang， Zhu Fei， Ling Xinghong， et al. Safe Q-learning me-thod based on constrained Markov decision processes［J］. IEEE Access， 2019， 7： 165007-165017.

［47］Park H， Sim M K， Choi D G. An intelligent financial portfolio trading strategy using deep Q-learning［J］. Expert Systems with Applications， 2020， 158： 113573.

［48］Ganger M， Hu Wei. Quantum multiple Q-learning［J］. International Journal of Intelligence Science， 2019， 9（1）： 1-22.

［49］Brandhofer S， Braun D， Dehn V， et al. Benchmarking the perfor-mance of portfolio optimization with QAOA［J］. Quantum Information Processing， 2022，22（1）： 25.

［50］Fernández-Lorenzo S， Porras D， García-Ripoll J J. Hybrid quantum-classical optimization with cardinality constraints and applications to finance［J］. Quantum Science and Technology， 2021，6（3）： 034010.

［51］Giurgica-Tiron T， Kerenidis I， Labib F， et al. Low depth algorithms for quantum amplitude estimation［J］. Quantum， 2022， 6： 745.

［52］Lloyd S， Mohseni M， Rebentrost P. Quantum principal component analysis［J］. Nature Physics， 2014， 10（9）： 631-633.

［53］Giri P R， Korepin V E. A review on quantum search algorithms［J］. Quantum Information Processing， 2017， 16： 1-36.

［54］Alcazar J， Leyton-Ortega V， Perdomo-Ortiz A. Classical versus quantum models in machine learning： insights from a finance application［J］. Machine Learning： Science and Technology， 2020，1（3）： 035003.

［55］An D， Linden N， Liu Jinpeng， et al. Quantum-accelerated multilevel Monte Carlo methods for stochastic differential equations in mathema-tical finance［J］. Quantum， 2021， 5： 481.

［56］Orús R， Mugel S， Lizaso E. Quantum computing for finance： overview and prospects［J］. Reviews in Physics， 2019， 4： 100028.

［57］Cao Yudong， Jiang Shuxian， Perouli D， et al. Solving set cover with pairs problem using quantum annealing［J］. Scientific Reports， 2016， 6（1）： 33957.

［58］Ajagekar A， Al Hamoud K， You F. Hybrid classical-quantum optimization techniques for solving mixed-integer programming problems in production scheduling［J］. IEEE Trans on Quantum Engineering， 2022， 3： 1-16.

［59］Sanders Y R， Berry D W， Costa P C S， et al. Compilation of fault-tolerant quantum heuristics for combinatorial optimization［J］. PRX Quantum， 2020，1（2）： 020312.

［60］Liu Zhe， Li Shurong. A numerical method for interval multi-objective mixed-integer optimal control problems based on quantum heuristic algorithm［J］. Annals of Operations Research， 2022， 311（2）： 853-898.

［61］Rebentrost P， Gupt B， Bromley T R. Quantum computational finance： Monte Carlo pricing of financial derivatives［J］. Physical Review A， 2018， 98（2）： 022321.

［62］Lu Junyi， Hu Yong， Li Xaoyu， et al. A new stock forecasting model by hidden quantum Markov models［C］//Proc of International Confe-rence on Artificial Intelligence and Security. Cham： Springer International Publishing， 2022： 438-447.

［63］Paquet E， Soleymani F. QuantumLeap： hybrid quantum neural network for financial predictions［J］. Expert Systems with Applications， 2022， 195： 116583.

［64］Liu Ge， Ma Wenping. A quantum artificial neural network for stock closing price prediction［J］. Information Sciences， 2022， 598： 75-85.

［65］Kartono A， Fatmawati V W， Wahyudi S T. Numerical solution of nonlinear Schrodinger approaches using the fourth-order Runge-Kutta method for predicting stock pricing［J］.Journal of Physics： Confe-rence Series， 2020， 1491（1）： 012021.

［66］Zhou L， Wang Shengtao， Choi S， et al. Quantum approximate optimization algorithm： performance， mechanism， and implementation on near-term devices［J］. Physical Review X， 2020， 10（2）： 021067.

［67］Gunjan A， Bhattacharyya S， Hassanien A E. Portfolio optimization using quantum-inspired modified genetic algorithm［C］//Proc of International Conference on Variability of the Sun and Sun-Like Stars： from Asteroseismology to Space Weather. 2022： 665-673.

［68］Woerner S， Egger D J. Quantum risk analysis［J］. NPJ Quantum Information， 2019， 5（1）： 15.

［69］Fiderer L J， Schuff J， Braun D. Neural-network heuristics for adaptive Bayesian quantum estimation［J］. PRX Quantum， 2021， 2（2）： 020303.

［70］Guo Mingchao， Pan Shijie， Li Wenmin， et al. Quantum algorithm for unsupervised anomaly detection［EB/OL］. （2023）. https：//arxiv.org/abs/2304.08710.

［71］Tapia E P， Scarpa G， Pozas-Kerstjens A. A didactic approach to quantum machine learning with a single qubit［J］. Physica Scripta， 2023， 98（5）： 054001.

［72］Grossi M， Ibrahim N， Radescu V， et al. Mixed quantum-classical method for fraud detection with quantum feature selection［J］. IEEE Trans on Quantum Engineering， 2022， 3： 1-12.

［73］Wiebe N， Kapoor A， Svore K M. Quantum nearest-neighbor algorithms for machine learning［J］. Quantum Information and Computation， 2015， 15（3-4）： 318-358.

［74］Amin M H， Andriyash E， Rolfe J， et al. Quantum Boltzmann machine［J］. Physical Review X， 2018， 8（2）： 021050.

［75］Coyle B， Henderson M， Le J C J， et al. Quantum versus classical generative modelling in finance［J］. Quantum Science and Technology， 2021，6（2）： 024013.

［76］Lewis M， Glover F. Quadratic unconstrained binary optimization problem preprocessing： theory and empirical analysis［J］. Networks， 2017， 70（2）： 79-97.

［77］Sack S H， Serbyn M. Quantum annealing initialization of the quantum approximate optimization algorithm［J］. Quantum， 2021， 5： 491.

［78］Carrascal G， Botella G， Del Barrio A， et al. A Bayesian-network-based quantum procedure for failure risk analysis［J］. EPJ Quantum Technology， 2023， 10（1）： 13.

［79］Miyamoto K， Kubo K. Pricing multi-asset derivatives by finite-diffe-rence method on a quantum computer［J］. IEEE Trans on Quantum Engineering， 2021， 3： 1-25.

［80］Abbas A， Sutter D， Zoufal C， et al. The power of quantum neural networks［J］. Nature Computational Science， 2021， 1（6）： 403-409.

［81］Bharti K， Cervera-Lierta A， Kyaw T H， et al. Noisy intermediate-scale quantum algorithms［J］. Reviews of Modern Physics， 2022， 94（1）： 015004.

［82］Cross A， Javadi-Abhari A， Alexander T， et al. OpenQASM 3： a broader and deeper quantum assembly language［J］. ACM Trans on Quantum Computing， 2022， 3（3）： 1-50.

［83］Dou Menghan，Zou Tianrui，Fang Yuan，et al. QPanda： high-performance quantum computing framework for multiple application scenarios［EB/OL］.（2022）. https：//arxiv.org/abs/2212.14201.