大单元教学视域下板书设计的关键思维

好的板书应体现一节课的精华，引导学生系统构建知识，启迪学生思维，促进知识迁移。本文基于数学新课程标准强调的大单元教学理念，提出板书设计策略，引导教师通过聚焦式思维、审辩式思维、系统式思维构建板书，以改变传统板书设计零散式呈现、浅层次梳理等问题，增强板书的思维含量，提高板书内容的思辨性和关联度，使之成为“种子模型”，促进学生数学眼光、数学思维和数学语言的发展。

一、聚焦式思维：由知识呈现到本质凸显

聚焦式思维指面对复杂问题时专注于识别问题的核心，并围绕这个核心进行思考和行动的思维方式。这样的思维方式有助于学生在数学原型中找到本质特征，通过转化、推理和抽象，理解数学本质。

教学人教版数学五年级下册第四单元《分数的意义》时，教师通常这样设计板书（如图1）。

从图1板书中，学生可以明确：本节课的主要知识点包括单位“1”、分数、分数单位等概念；“单位1”可以是一个物体、一个计量单位或一些物体等。这种板书虽然简洁地呈现了学习内容，但缺少深度，难以帮助学生深入理解分数的意义。

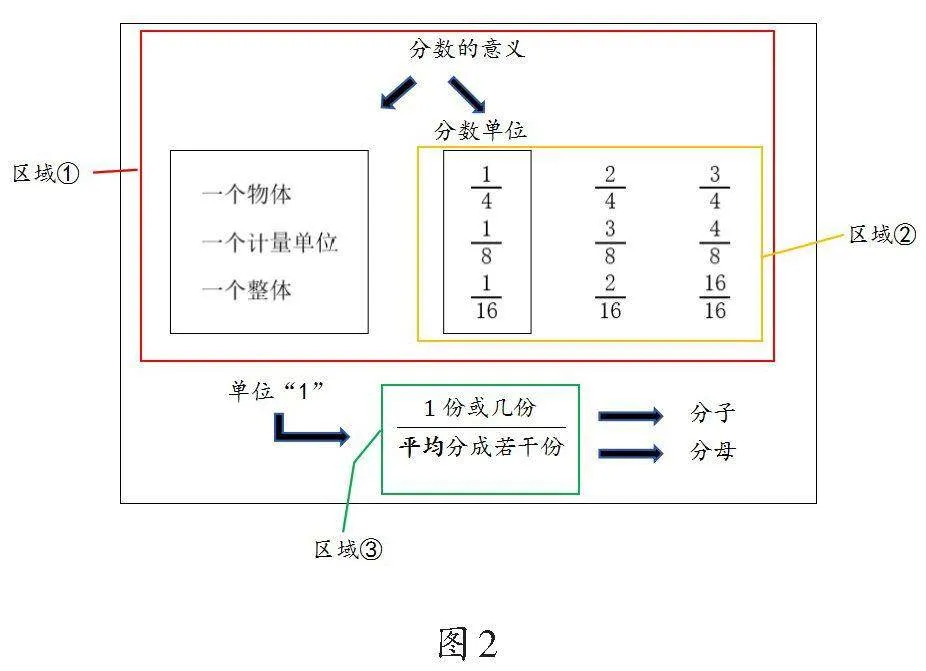
笔者通过聚焦式思维改进板书（如图2）。

图2板书凸显了聚焦式思维，抓住了知识的内在关联与核心要素。与图1板书对比，我们不难发现图2板书具有以下优势：区域①呈现“分”是把一个整体平均分成几份，“数”是取其中一份或者几份，这样就得到一个新的数——分数，这一设计体现了对知识本源的挖掘，有助于学生深度理解分数的产生和意义；区域②呈现分数单位与分数之间的关系，有助于学生理解“取一份，得到的分数就是分数单位”以及“有几个这样的分数单位，就是几分之几”；区域③体现了分数的模型，有助于学生体悟分数各部分的具体意义，而不是把分数当成一个抽象的名称。这样的板书有助于展现知识内涵，凸显数学原型。

二、审辩式思维：由方法归纳到理性辨析

审辩式思维是一种高阶思维，强调以审辩的视角有条理地思考、理性地思考。审辩式思维能帮助学生发现数学原理，探寻知识之间的不同及内在联系，实现深度学习。

教学人教版数学二年级下册第四单元《解决问题》时，教师通常这样设计板书（如图3）。

图3这种常规板书旨在引导学生学习提取题目中的信息，进行解答与检验，虽然呈现了思路清晰、过程完整的解题方法，但它以掌握知识为设计原则，思维含量不高，没有体现学习迁移思想。

笔者通过审辩式思维改进板书（如图4）。

图4板书用长条直观图呈现了两种除法原理：一种是“包含分”，求56元里面有几个8元；另一种是平均分，即把45元平均分成5份，求每份多少元。这样呈现有助于学生对比辨析除法的两种情况，发现它们的共性——同属于“总数÷每份数=份数”模型，理解它们的不同——一种是求每份数，一种是求份数。总的来说，审辩式思维下的板书设计注重展现思辨过程，注重方法指导、思想渗透和认知完善，有助于学生获得更高层次的数学理解，实现知识迁移。

三、立体式思维：由单一梳理到整体建构

立体式思维指从纵、横两个方向或从知识的深度、广度出发思考问题，它有助于学生开拓更多的思维通道。这些思维通道可辅助学生找到知识之间的关联，立体构建知识网络。

教学人教版数学四年级下册第四单元《小数的意义》时，教师通常这样设计板书（如图5）。

这种板书设计关注了小数的概念、特征和写法，但看不到小数计数单位之间的联系，看不到小数的组成，难以引导学生从“数”这个大概念出发，理解小数的意义。

笔者通过立体式思维改进板书（如图6）。

布鲁纳说：“学习的目的在于采用发现学习的方式，使学科的基本结构转变为学生头脑中的认知结构。”如图6所示板书通过结构化的计数单位阶梯模型，既横向呈现了小数各计数单位之间的关联，又纵向体现了整数计数单位与小数计数单位的贯通，将知识串成线、扩成面、形成体，便于学生理解和记忆。板书还借助数学尺的直观呈现，帮助学生感受小数单位的大小，让小数的概念有丰富度并显性化。这样的板书引导学生从数的大概念出发理解小数的意义，有助于学生认识一切数的组成都是“十进制”的产物。