促进学习进阶的“三个关注”

学习进阶指学生在学习和探究某一主题时，经历一个依次进阶、逐层深化的思维探究过程。学生在学习过程中会经历认知过程中的多个中间水平“阶梯”，这些“阶梯”构成了学习进阶链，将学生的学习起点和终点紧密连接起来，使课堂学习成为学生不断探索与发展的思维进阶之旅。如何在数学教学中促进学生实现学习进阶呢？笔者以一道非常规数学题的解题教学为例做具体阐释。

一、关注学习进阶的起点和终点

当前的数学考试评价对非常规问题的考查日益增多，教师需要思考如何通过分析学生的进阶起点和终点，合理设置学习目标，更好地帮助学生在解题过程中实现思维进阶。

下面是一道关于储物柜的非常规数学题。

学校有343名学生，有从1到343编号的343个储物柜。开学第一天，343名学生在校外就以下计划达成一致。第1名学生进入学校后，打开所有的储物柜。第2名学生进入学校后，关闭每个编号为偶数的储物柜。第3名学生将编号为3的倍数的储物柜“倒转”一次，即同原来储物柜的开关状态相反。第4名学生将编号为4的倍数的储物柜“倒转”一次。以此类推，直到343名学生依次进入学校并“倒转”相应编号的储物柜。哪些储物柜最终会保持打开状态？

这道题的条件信息、目标信息、运算信息都不明确，八年级学生很难仅凭记忆或原有经验解题。教师在分析学生进阶起点时，应关注学生的心理状况、已有知识、认知盲点等，并据此设定学习目标。学生学习进阶的起点是其原有的认知结构，八年级学生已经学习“因数与倍数”“平方数的认识”，认知模糊点和盲点是“平方数的因数个数特征”。基于以上分析，教师将本节课的学习进阶终点设置为：学生能够理解并掌握“平方数的因数个数始终为奇数的推理过程”，能用列表和逻辑推理两种方法解答；经历数学探究过程，培养观察、猜想、验证、推理等能力，并掌握转化、归纳的思想；学会打破思维定势，敢于提出质疑，能够用多种途径或方法解决问题，提升发散思维能力。

二、关注思维发展阶点的支架设置

在学习过程中，教师要在学生学习的每个阶点精心设计“思维支架”，助力学生“爬阶梯”，引领学生从低阶思维向高阶思维发展。课堂上，教师出示这道非常规问题后，学生发现面临的问题非常多，比如，如何准确把握题目意思、采取何种方法解题等。这就需要教师在教学过程中设置不同支架，引领学生跨越每个思考阶点。

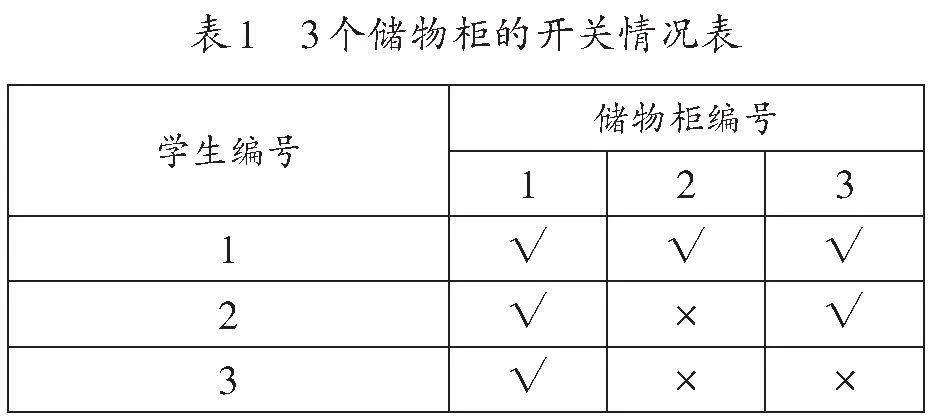
首先，在学生没有解题思路时，教师提供方法思路支架，引导学生分析问题。如，教师提出“储物柜数量太多导致解题很困难，我们为什么不从少一点的储物柜开始尝试呢？”学生自然想到“化繁为简”的方法，随即在数量少的情况下展开探究。在学生动手尝试后，教师收集展现学生思考过程的作品（见表1、表2，“√”代表储物柜被打开，“×”代表储物柜被关闭），并用投影展示。

当储物柜个数为3时，1号学生开关储物柜之后，1～3号储物柜都用“√”表示打开状态；2号学生开关储物柜之后，2号储物柜由开变成关，就由“√”变成“×”。

在学生完成上述推理之后，教师引导学生观察两个表格。学生比较后发现，额外增加一个储物柜并不会改变之前的储物柜开关情况。继续观察上述表格，学生发现编号1下面有很多重复的“√”，编号2下面有很多重复的“×”，这些重复的“√、×”干扰了他们的思考。于是，教师引导学生思考，如何借助简化版的列表解决问题。学生通过推理画出9个储物柜开关情况的简化版列表（见表3）。

接着，各小组展开讨论，小组代表汇报各小组的思考成果。大部分学生认为，观察简化版表格的对角线，可以清晰地看到最终哪些储物柜被打开。这时，学生遇到的问题是，不知道最后被打开的储物柜编号数字有什么规律，难道要一直这样列表推理吗？

其次，在学生思维无法突破时，教师给出关键问题支架，引导学生思考规律。教师给出第一个问题支架：“你能发现是哪些储物柜的编号数字始终操控储物柜的开关吗？”学生根据提示分析，发现最终打开的是编号为1，4，9等平方数的储物柜，从而猜测编号为1～343内的所有平方数的储物柜最终都能被打开。教师给出第二个问题支架：“每一次能控制储物柜开或关的数字有什么规律？”学生开始纵向观察表3，发现编号为8和9的储物柜编号数字的因数个数能操控储物柜的开关，例如编号数字8的因数（1，2，4，8）为偶数个，所以储物柜经过多次“开”“关”的循环后，最后被“关闭”；编号数字9的因数（1，3，9）为奇数个，经过“开”“关”的循环后，最终一定剩下一个因数对应“开”，所以储物柜最终被打开。由此，学生明确：可根据“一个数字的因数个数是否为奇数个”判断储物柜最终是否被打开。

最后，在学生思维需要提升时，教师给出定理支架（因数个数定理），引导学生运用定理分析问题。学生将之前的猜测“平方数最终被打开”与“编号数字因数为奇数个的储物柜最终被打开”相联系思考，发现可以得到一个新的问题：是否所有因数为奇数个的数都是一个平方数？这时，教师可以举例讲解因数个数定理：一个数的因数是由其所有质因数的指数加1后的乘积决定的，如60可以分解为“60=[22]×3×5”，那么60的因数个数用“（2+1）×（1＋1）×（1+1）”计算，是12个，

三、关注验证学习进阶的评价

在基于学习进阶的评价中，教师通过诊断并记录学生目前所处的认知阶段，以及展示学生可能实现思维进阶的路线，关注学生思维发展的情况，了解学生学习进阶的情况。

在教学中，教师分发给学生一张提前设计好的解题记录与评价单。学生在单子上记录思路或者问题，教师通过检查学生的记录及时了解他们处于思维进阶的哪个阶段，他们能否从不同角度探索问题、从不同层面分析问题，从而为改进教学和学习提供有效的依据。解题记录与评价单主要包括三个部分：一是理解问题部分，通过判断学生能否用简洁的语言重述问题，评价学生对问题的思考程度，如让学生准确回答出1～3号学生操作储物柜之后，有哪些储物柜最终被打开；二是拟订计划部分，通过判断学生的解题计划是部分正确还是完全正确，评价学生的思考是否有提升、学生是否遇到思维阻碍、学生的思考如何进阶；三是检查和拓展部分，通过判断学生是否有多种解题方法，评价学生是否具有发散性思维，如观察学生能否采取“列表”和“分析数字因数个数”等方法解答问题等。