学习二元一次方程组，感悟消元转化思想

领 衔 人：李庾南（特级教师、正高级教师）

组稿团队：江苏省李庾南数学教学研究所

在“二元一次方程组”这一章，同学们需要了解二元一次方程、二元一次方程组及其相关概念，理解二元一次方程组的求解思想和求解方法，特别是通过“二元”向“一元”转化，感受事物之间是普遍联系、相互转化的辩证思想。让我们从“两数之和”“两数之差”的问题出发，开始二元一次方程（组）概念及解法的学习之旅吧！

问题1 已知两个数的和等于8，求这两个数。

讲解：易设这两个数分别为x、y，由题意建立方程x+y=8。这样就可以概括二元一次方程的概念：像“x+y=8”这样，含有两个未知数，并且未知数的指数都是1的整式方程叫作二元一次方程。使二元一次方程两边的值相等的两个未知数的值，叫作二元一次方程的解。那么，如何求x+y=8的解呢？

二元一次方程的一个解是一对未知数的值。两个未知数的值是相互制约的，所以记作：[x=1，y=7，][x=0，y=8，][x=-2.5，y=10.5，]等等，x、y这两个数虽相互制约，但不唯一。一般地，二元一次方程有无数个解。

问题2 已知两个数的差是2，求这两个数。

讲解：设这两个数中的较大的数为x，较小的数为y， 则x-y=2。

∴[x=0，y=-2，][x=-1，y=-3，x=1， y=-1， ]等等。

同样，这样的数组也不是唯一的。

问题3 已知两个数的和为8，两个数的差为2，求这两个数。

讲解：设这两个数中较大的数为x，较小的数为y。

由题意得[x+y=8，①x-y=2，②]

把这样的两个含有相同未知数的二元一次方程合在一起，就组成了一个二元一次方程组。二元一次方程组的两个方程的公共解，叫作二元一次方程组的解。

接下来，我们就来找出方程组[x+y=8，①x-y=2 ②]的解，即方程①②的公共解。

方法一：①+②，消去y，得x=5。

将x=5代入方程①或②，得y=3。

∴方程组的解为[x=5，y=3。]

方法二：①-②，消去x，得y=3。

将y=3代入方程①或②，得x=5。

∴方程组的解为[x=5，y=3。]

可见，二元一次方程组的求解思想是“消元”。将未知数的个数由多化少、逐一解决的想法，叫作消元思想。以上解法叫作加减消元法，即当两个二元一次方程中同一未知数的系数互为相反数或相等时，将两个方程的两边分别相加或相减，就能消去这个未知数，得到一个一元一次方程，可简称加减法。

那么，解方程组[x+y=8，①x-y=2，②]有没有其他消元的方法呢？

比如，由②，得x=y+2，③

（将一个未知数用含另一个未知数的式子表示）

把③代入①，

（“代入”，根据是“等量代换”）

得y+2+y=8。

（消去x，得关于y的一元一次方程）

解这个方程，得y=3。

（解出一个未知数）

把y=3代入③，

（“回代”，即代入“关系式”）

得x=3+2。

解得x=5。

∴方程组的解为[x=5，y=3。]

像上面这样，将二元一次方程组中的一个方程，变形为“一个未知数用含有另一个未知数的式子表示”的形式，再代入另一个方程，实现消元，进而求得这个二元一次方程组的解，这种方法叫作代入消元法，简称代入法。

最后，让我们一起回顾解方程组[x+y=8，①x-y=2 ②]的过程。

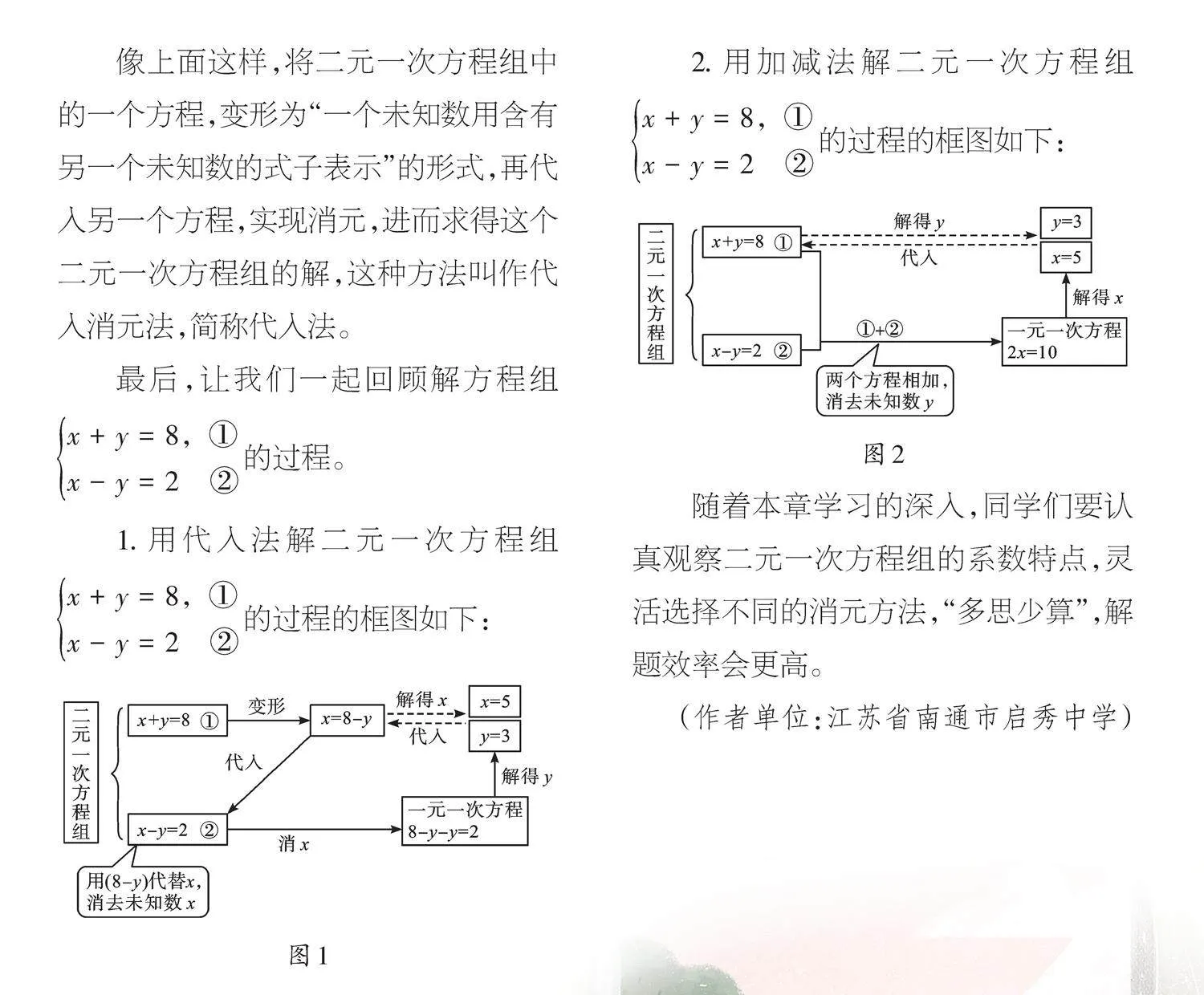
1.用代入法解二元一次方程组[x+y=8，①x-y=2 ②]的过程的框图如下：

2.用加减法解二元一次方程组[x+y=8，①x-y=2 ②]的过程的框图如下：

随着本章学习的深入，同学们要认真观察二元一次方程组的系数特点，灵活选择不同的消元方法，“多思少算”，解题效率会更高。

（作者单位：江苏省南通市启秀中学）