基于不经意多项式估值的SM4协同加解密方案

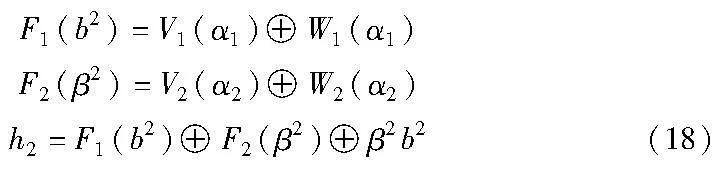
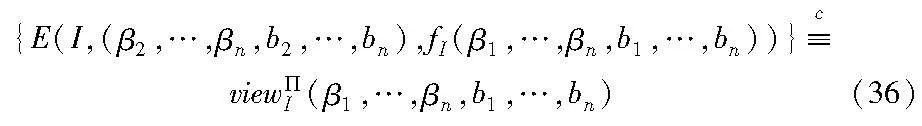
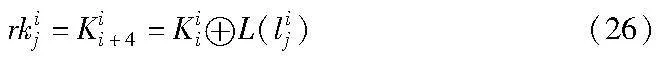
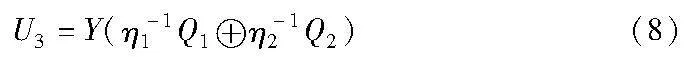
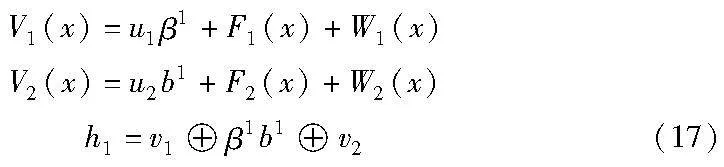
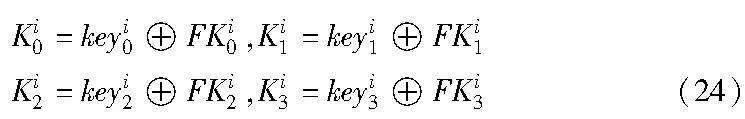
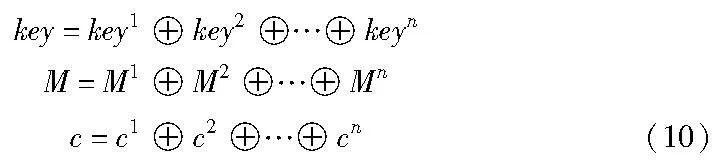
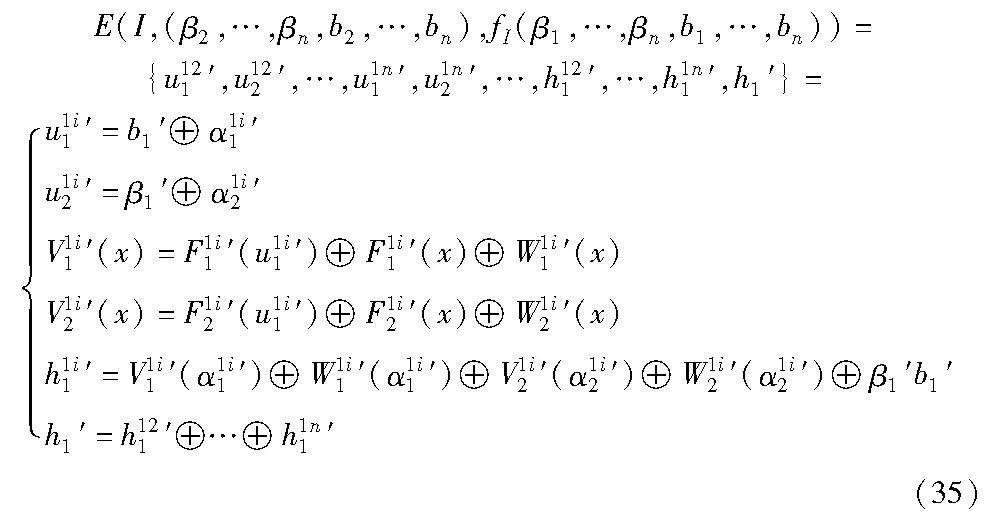
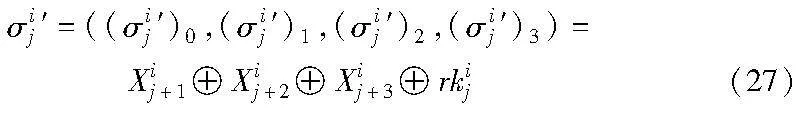
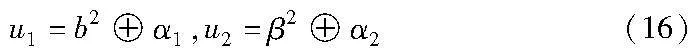
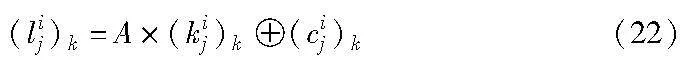
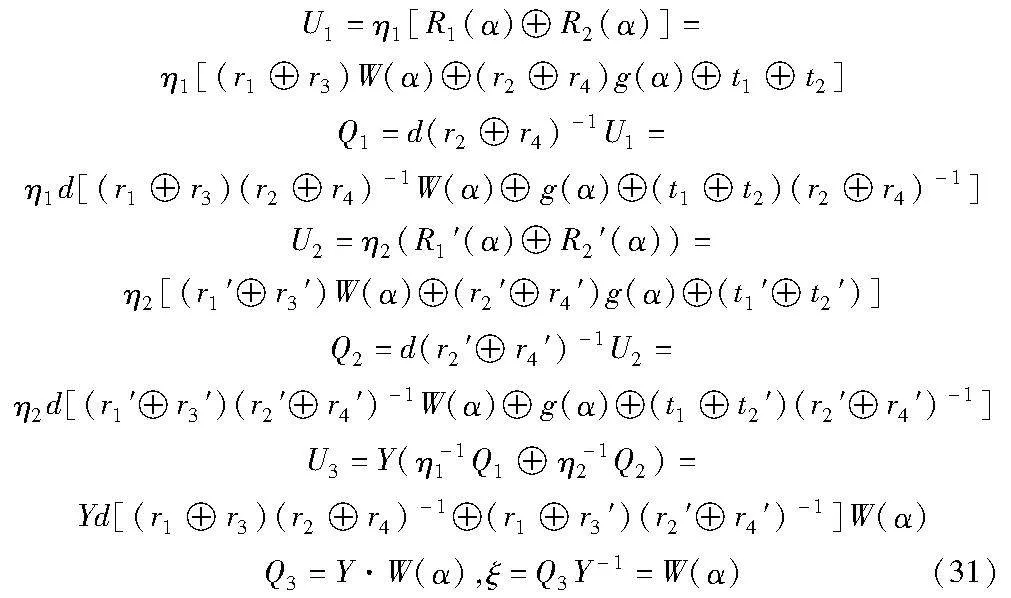
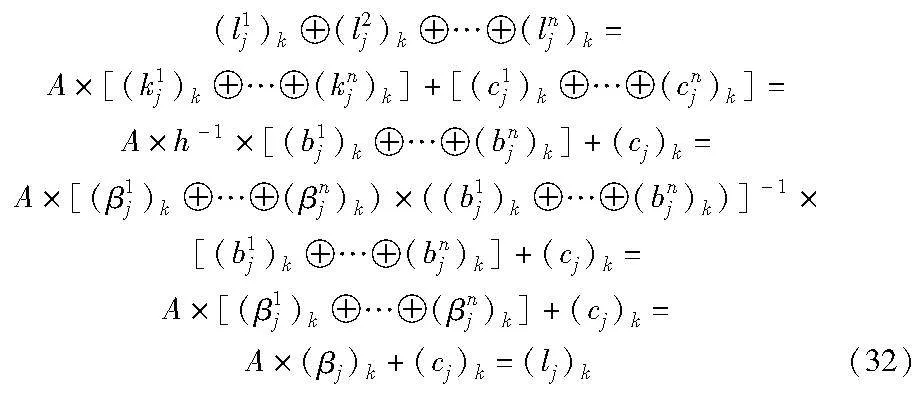
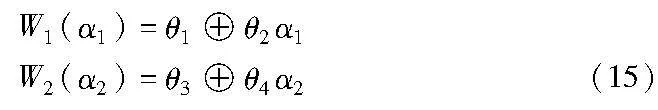
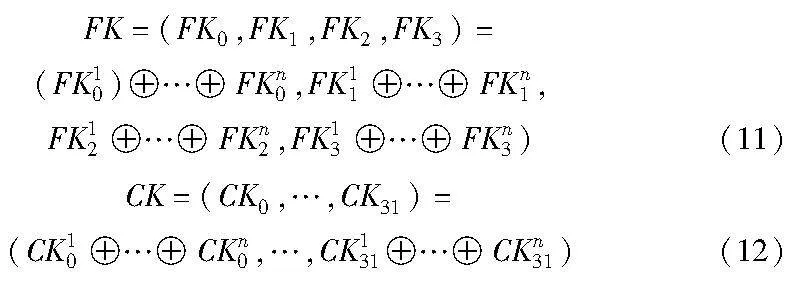
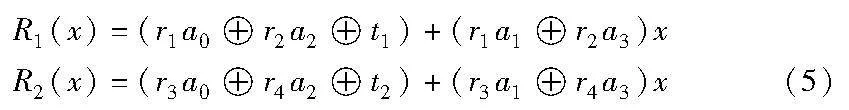
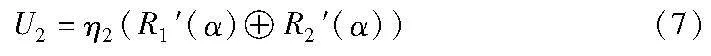
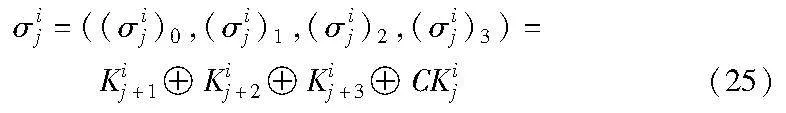
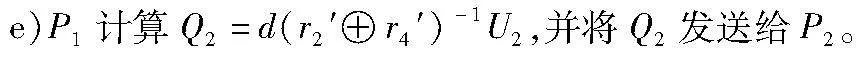
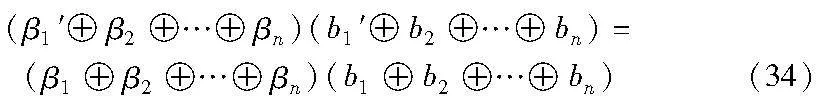
摘 要：协同加解密是安全多方计算中的重要研究方向，它可以安全高效地实现数据保护、隐私保护。为解决现有SM4协同加解密方案离线计算阶段计算复杂度偏高的问题，提出一种基于不经意多项式估值的SM4协同加解密方案。方案利用预计算的多项式集合和多项式值集合来完成在线阶段的S盒协同计算，从而提高在线计算阶段的性能。其证明了所提方案的正确性和安全性，同时与四种不同的方案进行对比，结果表明，所提方案计算效率明显高于其他方案，说明所提方案能安全高效地完成SM4协同加解密。

关键词：安全多方计算； 协同加解密； SM4； 不经意多项式估值

中图分类号：TP309 文献标志码：A

文章编号：1001-3695（2024）06-038-1862-07

doi：10.19734/j.issn.1001-3695.2023.09.0432

SM4 collaborative encryption and decryption scheme based onoblivious polynomial evaluation

Abstract：Cooperative encryption and decryption is an important research direction in secure multi-party computation. It can achieve data protection and privacy protection safely and efficiently. To solve the problem of high computational complexity in the offline calculation phase of existing SM4 collaborative encryption and decryption schemes， this paper proposed a new SM4 collaborative encryption and decryption scheme based on oblivious polynomial evaluation. The scheme utilized pre-calculated polynomial sets and sets of polynomial values to complete S-box collaborative computation in the online stage， thereby improving the performance of the online calculation stage. This paper proved the correctness and security of the proposed scheme， and compared with four different schemes，the results show that the computational efficiency of the proposed scheme is significantly higher than that of other schemes. This shows that the proposed scheme can complete SM4 cooperative encryption and decryption safely and efficiently.

Key words：secure multi-party computation; collaborative encryption and decryption; SM4; oblivious polynomial evaluation

0 引言

随着信息技术和通信技术的迅速发展，以及人们对网络安全和数据隐私保护的日益关注，作为一个拥有庞大人口和复杂安全环境的国家，保护个人隐私、商业机密和国家机密已经成为了目前面临的一项重要挑战。在这种背景下，建立具备自主知识产权的加密系统，成为了政府推动信息化建设、保障国家安全的一个紧迫问题。SM4正是针对上述需求而推出的一款符合国际标准、具有自主知识产权、能够满足不同安全等级需求的分组密码算法。在多个组织或参与者之间共享和协作处理敏感数据时，需要确保各自数据的机密性和安全性，由于集中式加解密方式存在单点故障和中心化信任问题，不再适用。

协同加解密技术可以防止单点故障和黑客攻击，其理论和算法建立在安全多方计算［1］和密码学的基础上，可以有效应对信息处理中的安全问题。它采用了类似于区块链技术的去中心化模型，允许多方在不需要可信第三方的情况下协同加解密，从而获取敏感数据。在传统的加密方式中，一般都是由一方来掌握加解密的权限，这可能会导致数据难以共享，同时也存在被窜改和泄露的风险。协同加解密技术将数据和加解密的控制权分布到整个网络中的节点，使得每一个节点都具有数据加解密的能力，密钥也被分散存储在多个节点上，从而降低了密钥被攻击的风险，能够更好地保证数据隐私和安全。尽管协同加解密技术在实现时存在很多难题，并且需要合适的环境和基础设施支撑，但是它为数据共享和计算提供了一种全新的解决方案。

最早的协同计算方案大多基于1979年Shamir［2］提出的门限秘密共享方法。该方法将密钥分成n份，并分别由n个参与方保存。然后设置一个特定的门限值t。只有当参与方的数量大于或等于t时，这些参与方才可以通过多项式插值的方法恢复出完整的密钥，然后完成签名或者解密操作。但这种方法存在一定的安全隐患，参与方在获得完整密钥后，即可在其他参与方不知情的情况下使用密钥。MacKenzie等人［3］提出一种DSA两方协同签名的方案，将私钥分割后分别存储在两个实体中，双方都不能单独生成合法的DSA签名，只有通过一系列的交互后才可以协同完成签名或解密，全程不会暴露双方的私钥。Mu等人［4］提出一种SM9两方协同签名的方案，保证双方不需要重构出完整私钥的情况下，通过协作能输出合法的SM9签名。徐彬彬等人［5］提出了支持门限的分布式SM2/SM9算法，但算法中引入了同态加密，算法的计算复杂度较高。Lindell［6］提出一种基于Paillier同态加密算法的两方ECDSA协同签名方案，规避了大量零知识证明，利用Paillier算法的同态性质来完成两方协同签名，但由于方案中引入了Paillier同态加密算法，方案的性能有待提高。颜萌等人［7］提出了一种高效的两方ECDSA门限方案签名，将签名分为预计算阶段和在线签名阶段，将在线签名阶段的同态操作转移到预计算阶段，加快了在线签名阶段的计算速度。严都力等人［8］提出了一种抗差分故障攻击的两方协同EdDSA签名方案，但也借助了Paillier同态加密算法。Doerner等人［9］提出了一种基于秘密共享和不经意传输技术的协同计算方案，由于引入了不经意传输技术，通信量和通信次数比较高。文嘉明等人［10］提出了一种基于非对称模格问题的两方协同Aigis签名，能有效缩减签名的尺寸。关于公钥密码协同计算的研究都集中在RSA协同签名、ECDSA协同签名［11，12］、SM2/9协同签名。

不经意多项估值协议作为一种两方安全的多方计算协议，可以作为很多安全多方计算协议实现的基础。Dttling等人［13］提出了一个两方安全多方计算协议，其中两个参与者使用不经意多项式估值在预计算阶段完成乘法三元组的计算。杨博为等人［14］提出了一种三方不经意多项式求值协议，协议利用Diffie-Hellman密钥交换协议和安全的不经意传输来实现。Cianciullo等人［15］提出用不经意多项式估值来计算安全多方计算中的乘法，与使用Beaver乘法三元组的方法相比，减少了计算乘法时所需参与方数量，降低了通信复杂度。Cianciullo等人［16］将分布式不经意传输协议改编为灵活的分布式不经意多项式估值协议，同时创建了第三方不经意多项式估值协议的三个扩展。

从公开的文献来看，对称密码协同计算的研究并不多。杨伊等人［17］提出了一种密钥管理服务系统下的安全高效的多方协同SM4加/解密方案。该方案利用Beaver乘法三元组［18］来实现S盒协同计算的高效性和安全性，但生成Beaver乘法三元组时需要用到同态加密，而同态加密需要进行复杂的数学运算，其计算量大、速度慢，需要更多的计算资源和存储空间。

本文基于不经意多项式估值协议设计了一种新的SM4协同加解密方案，该方案由离线预计算阶段和在线计算阶段组成，预计算阶段执行不经意多项式估值协议后，参与方能分别获得多项式集合和多项式值的集合。在线计算阶段的关键在于S盒协同计算，各参与方利用预计算阶段计算得到的多项式集合和多项式值的集合进行S盒协同计算。由于预计算阶段的不经意多项估值协议是采用引入随机函数的方法而不是同态加密，提高了SM4协同加解密的运算性能。

1 预备知识

1.1 半诚实模型及其安全性定义

定义1 半诚实模型下协议的安全性［19］。当参与者都是半诚实参与者时，若存在概率多项式时间算法E，使得对于任意的I，都有式（2）成立：

1.2 SM4算法

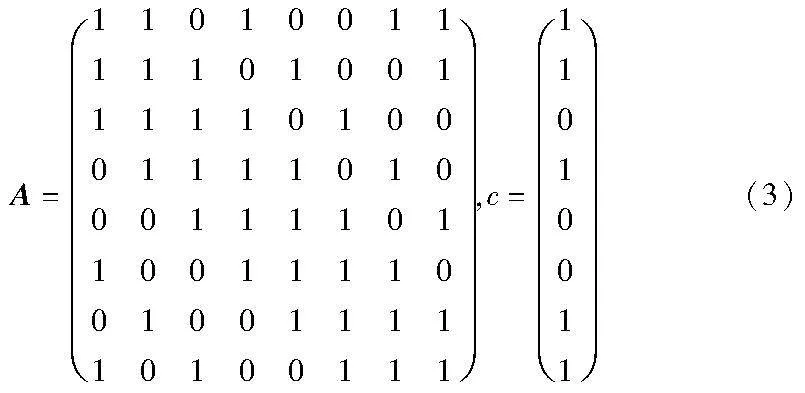
SM4［20］是我国自主设计的分组密码算法。该算法的分组长度和密钥长度均为128 bit。加密算法与密钥扩展算法都采用32轮非线性迭代结构。SM4采用了Feistel结构，解密算法与加密算法的结构相同，只是轮密钥的使用顺序相反，解密轮密钥是加密轮密钥的逆序。S盒是SM4的关键部分，查表实现是S盒最基本的实现方法，还有一种是通过多项式运算来实现的。SM4的S盒定义在GF（28）上，该伽罗瓦域采用的不可约多项式M（x）是x8+x7+x6+x5+x4+x2+1，S盒的生成方式为S（x）=A（Ax+c）-1+c，其中：

1.3 不经意多项式估值

不经意多项式估值（oblivious polynomial evaluation，OPE）是Naor等人 ［21］在1999年首次提出的。一个OPE协议有一个发送方和一个接收方，发送方S拥有一个私密多项式W（x），接收方R拥有一个私密值α。OPE协议执行完成后，接收方R只能得到W（α），发送方S得不到任何信息，同时保证发送方的W（x）不泄露。

2 方案设计

安全多方计算允许n个相互不信任的参与方在其私密输入不泄露的前提下，安全计算任何给定函数。就效率和通信复杂性而言，安全多方计算协议中的乘法运算一直是瓶颈。当前协议大多数采用的典型方法是使用Beaver乘法三元组来完成乘法运算，该方法依赖于同态加密或不经意传输。文献［13］介绍了一种基于不经意多项式估值的安全多方计算协议，该协议虽然也依赖于一些预先计算的信息，但在效率和通信复杂性上都要优于基于Beaver乘法三元组的安全多方计算协议。

SM4的运算可以分为线性运算和非线性运算，非线性运算即S盒运算，除S盒运算外都是线性运算。现有的协同加解密的思路大多都基于秘密分享，但是由于S盒运算是非线性的，所以仅仅对SM4的密钥、明文等其他参数进行秘密分享是无法实现正确的SM4协同加解密的。实现SM4协同加解密的关键在于实现S盒的协同计算结果与原始SM4的S盒输出结果相同。文献［17］提出了一种对S盒进行协同设计来实现SM4协同加解密的方法，其中S盒协同计算通过Beaver乘法三元组来实现安全两方乘法，但是Beaver乘法三元组的生成需要用到同态加密，计算开销大。

本文是在文献［17］对S盒协同计算来实现SM4协同加解密的思路上，对其方案进行改进，利用不经意多项式估值来实现S盒协同计算时需要的安全的两方乘法运算，从而实现比文献［17］方案更高效的SM4协同加解密。

本文提出的SM4协同加解密方案分为预计算阶段和在线计算阶段两部分，其中预计算阶段执行不经意多项式估值协议，为在线计算阶段的S盒协同计算部分的两方安全乘法作准备。在线计算阶段包括密钥与消息分配、S盒协同计算、密钥协同扩展和协同加解密四个部分。由于SM4采用的是Feistel结构，加解密的结构对称，只是轮密钥的使用顺序相反，所以本文只对协同加密（图1）进行描述。协同加密的具体过程在下文展开描述，其中加密算法与密钥扩展算法都采用32轮非线性迭代结构。

2.1 符号及定义

本文方案的符号及定义如表1所示。

2.2 预计算阶段

以两个参与方为例，参与方P1随机选择a0，a1∈GF（28）构造多项式W（x）=a0+a1x。参与方P2随机选择α∈GF（28）。协议执行完后，参与方P1不泄露其多项式，参与方P2获得多项式值W（α）。不经意多项式估值协议（图2）具体过程如下：

a）P1随机选取a2，a3，r1，r2，r3，r4，t1，t2∈GF（28），计算g（x）、R1（x）和R2（x）为

g（x）=r2+r3xR1（x）=r1W（x）+r2g（x）+t1R2（x）=r3W（x）+r4g（x）+t2（4）

GF（28）中的元素都是次数小于或等于8的多项式，多项式的加法可以转换成其对应2进制数的异或，所以R1（x）和R2（x）可以表示为

并将R1（x）和R2（x）发送给P2。

并将Q1、R1′（x）和R2′（x）发送给P2。

d）P2随机选取η2∈GF（28），计算U2为

并将U2发送给P1。

f）P2随机选取Y∈GF（28），计算U3为

并将U3发送给P1。

g）P1计算Q3为

并将Q3发送给P2。

h）P2计算ξ=Q3Y-1=W（α）。

2.3 密钥与消息分配

该阶段完成密钥、消息、系统参数的分配，将加密密钥key、明文M、系统参数FK、系统参数CK、S盒仿射变换使用的c都分割成n份，分别发送给n个参与方。

2.4 S盒协同计算

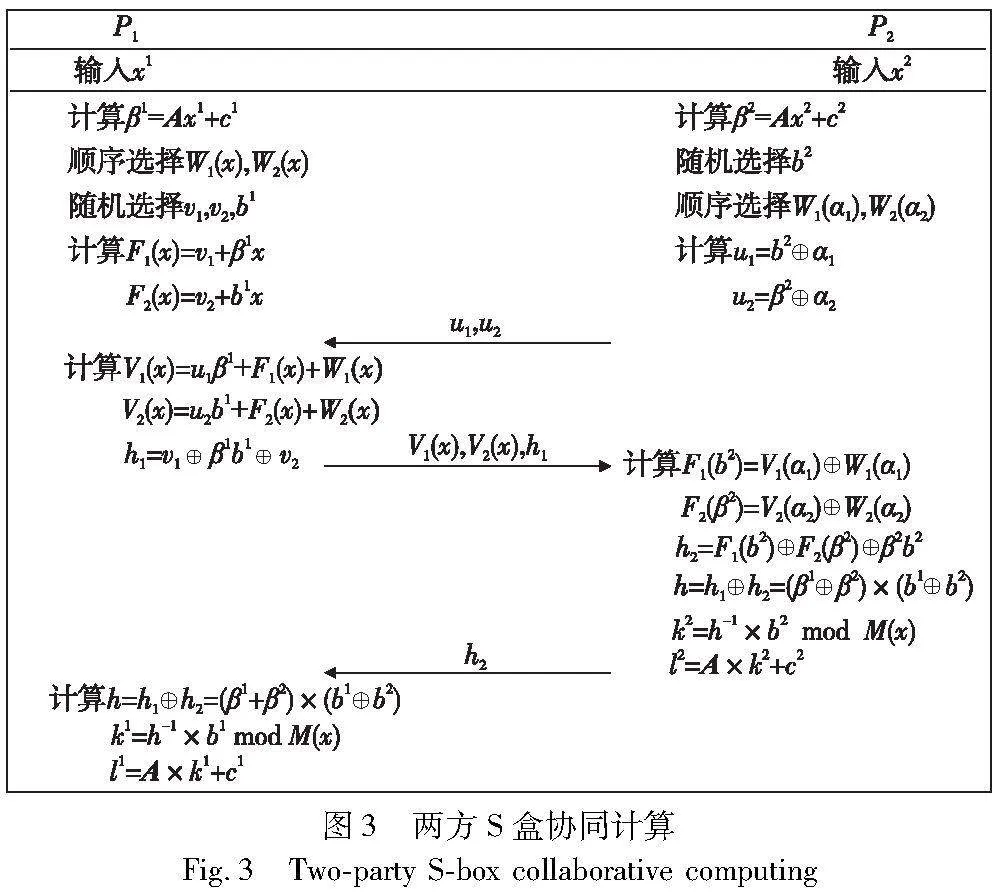
每个参与方借助预计算阶段计算得到的多项式集合和多项式值的集合与剩下的n-1个参与方两两协同计算，各自获得S盒的输出，具体过程如下：

（a）P1的S盒输入为x1，P1计算第一次仿射变换后的中间值β1为β1=Ax1+c1。P2的S盒输入为x2，P2计算第一次仿射变换后的中间值β2=Ax2+c2。

（b）P1从预计算阶段生成的多项式集合中顺序选择W1（x）和W2（x）为

W1（x）=θ1+θ2x，W2（x）=θ3+θ4x（13）

P1随机选取v1、v2，b1∈GF（28），得到F1（x）和F2（x）为

F1（x）=v1+β1x，F2（x）=v2+b1x（14）

（c）P2随机选取b2∈GF（28），并且从多项式集合中顺序选择W1（α1）和W2（α2）为

P2计算u1、u2并将其发送给P1。

（d）P1计算V1（x）、V2（x）、h1，并将其发送给P2。

（e）P2计算F1（b2）、F2（β2）、h2，并将h2发送给P1。

（f）此时双方都能计算出h为

b）Pi与剩余的参与方两两执行安全两方乘法后，将各自的hi发给剩余的参与方，所有参与方都能计算出h为

Pi先计算（kij）k为

（kij）k=h-1×（bij）kmod M（x）（21）

然后进行第二次仿射变换计算得到（lij）k为

最终，Pi的S盒协同计算的结果为

lij=（（lij）0，（lij）1，（lij）2，（lij）3）（23）

2.5 密钥协同扩展

密钥协同扩展的过程除了将原始SM4的S盒计算部分替换成S盒协同计算，其他部分都和原始SM4一样。n个参与方协同计算出各自的轮密钥rkij。

Pi拥有部分密钥keyi=（keyi0，keyi1，keyi2，keyi3），首先计算Ki0、Ki1、Ki2、Ki3为

然后，对于j=0，1，2，…，31，Pi操作如下：

a）计算σij为

将σij作为4个S盒的输入。n个参与方进行S盒协同计算后，得到各自的S盒输出为lij。

b）计算轮密钥rkij为

2.6 协同加密

协同加密的过程与密钥协同扩展的过程基本相同，只是将其中的线性变换L修改为L′。每个参与方都拥有部分明文Mi和轮密钥rkij 。从第1轮（j=0）到第32轮（j=31），Pi循环执行以下操作：

a）Pi拥有部分明文Mi=（Xi0，Xi1，Xi2，Xi3），计算σij′为

Pi将σij′分别作为4个S盒的输入。n个参与方进行S盒协同计算后，得到各自的S盒输出为lij′。

b）用S盒的输出来计算Xij+4为

经过32轮协同加密后，Pi得到部分密文Ci为

Ci=（Xi35，Xi34，Xi33，Xi32）（29）

将所有参与方的部分密文合并得到最终的密文为

3 安全性证明

3.1 正确性分析

本文方案关键在于预计算阶段的不经意多项式估值协议和在线计算阶段的S盒协同计算。在线计算阶段的S盒协同计算利用安全多方计算，保证多方交互过程中各方拥有的秘密值不被泄露以及最终结果的正确性，其他部分都和原始SM4保持一致。因此，本文方案的正确性分析主要是针对预计算阶段的不经意多项式估值协议和在线阶段的S盒协同计算两部分进行的。

a）不经意多项式估值协议的正确性分析。

b）S盒协同计算的正确性分析。

S盒协同计算是正确的，等价于各参与方S盒协同计算输出异或起来的结果与原始SM4算法S盒输出是一致的。

这样就保证了n个参与方协同计算后，各自得到的S盒输出全部异或之后的结果和原始SM4的S盒输出是一致的。因此，本文方案中的S盒协同计算是正确的。

两方SM4协同加密结果如图4所示，两方密文异或结果与原始SM4加密的密文一致，因此本文的SM4协同加密方案是正确的。

3.2 安全性分析

本方案分为预计算阶段和在线计算阶段，需对两个阶段都进行安全性证明。预计算阶段主要是参与方两两多次执行不经意多项式估值协议生成多项式集合、多项式值的集合，为在线计算阶段的S盒协同计算安全乘法部分做准备。在线计算阶段是在SM4基础上，利用不经意多项式估值协议进行S盒协同设计。SM4的安全性建立在底层结构和多轮迭代上，本文方案基于不经意多项式估值协议的S盒协同计算并没有破坏SM4底层结构和多轮迭代。因此，本文方案的安全性分析主要针对预计算阶段的不经意多项式估值协议以及在线计算阶段的S盒协同计算。

a）不经意多项式估值协议的安全性分析。

不经意多项式估值协议的安全性分为两方面：一方面是协议结束后发送方不能获得接收方所得的份额（α，W（α））的任何信息。另一方面是协议结束后，接收方只能得到份额（α，W（α）），除此之外不能得到任何有关W（x）的信息。

（a）协议结束后，发送方不能获得接收方所得的份额（α，W（α））的任何信息。

证明 由协议可知，发送方从接收方得到的信息为U1、U2、U3三个等式计算得到的数值。接收方在每个等式中都引入了一个随机数，分别为η1、η2、Y。接收方的α对于发送方来说也是一个随机数。未知数个数为4，方程个数为3，未知数个数大于方程个数，因此发送方无法计算出接收方的α。

（b）协议结束后，接收方只能得到份额（α，W（α）），除此之外不能得到任何有关W（x）的信息。

b）S盒协同计算的安全性。

现在借助模拟器的概念来证明S盒协同计算的安全性。

证明 因为在S盒协同计算的过程中，所有参与方的地位是相同的，所以诚实的参与方能受到最大的安全威胁就是其他所有参与方合谋企图获得该诚实参与方的隐私输入。这些攻击者构成的集合称为最大合谋攻击者集合。如果协议对最大合谋攻击者集合是安全的，显然对于最大合谋攻击者集合的任何子集都是安全的。假设P1是诚实的参与方，最大合谋攻击者集合为I={P2，P3，…，Pn}。

在协议执行过程中，I作为一个整体收到的消息只有u121，u122，…，u1n1，u1n2和h121，…，h1n1以及最后用于计算h值的h1。那么在协议执行过程中，I的视图为

viewΠI（β1，…，βn，b1，…，bn）=

{u121，u122，…，u1n1，u1n2，…，h121，…，h1n1，h1}（33）

接下来本文通过构造模拟器S来证明协议的安全性。E的模拟过程如下：

（a）接收输入 （I，（β2，…，βn，b2，…，bn），fI（β1，…，βn，b1，…，bn）），随机选择β1′，b1′∈GF（28），使得

（b）随机选择v121′，v122′，…，v1n1′，v1n2′∈GF（28），构造多项式F121′（x），F122′（x），…，F1n1′（x），F1n2′（x）。

（c）随机选取α121′，α122′，…，α1n1′，α1n2′∈GF（28）为不经意多项式的私密值，随机构造多项式W121（x），W122（x），…，W1n1（x），W1n2（x）。

（d）E模拟协议中的所有成员（模拟的P1不参与合谋）执行协议得到

在P1不参与合谋的情况下，在I的视角下，u121，u122，…，u1n1，u1n2和u121′，u122′，…，u1n1′，u1n2′都是GF（28）中的随机数，它们是计算不可区分的。同样地，h121，…，h1n1，h1和h121′，…，h1n1′，h1′也都是GF（28）中的随机数，它们也是计算不可区分的。

（e）因而得到

因此，本文的S盒协同计算在半诚实模型下是安全的。综上所述，本文方案在半诚实敌手模型下是安全的。

4 性能分析及实验验证

4.1 计算量分析对比

在半诚实敌手模型下，将公钥密码协同签名看作特殊的加密，用文献［6，7，17，22］与本文方案对同一明文进行两方协同加密，对5个方案进行对比分析。加减法的计算量远小于椭圆曲线上的点乘运算计算量、Paillier加密及解密计算的计算量、求逆运算的计算量、普通乘法的计算量，因此在分析计算量时，本文忽略加减法的计算量，把一次椭圆曲线上的点乘运算的时间记为Td，Paillier加密或解密计算时间记为Tp，将求逆运算的时间记为Ti，将一次普通乘法的时间记为Tm，将一次关于循环群上椭圆曲线离散对数关系的零知识证明时间记为Tzk。普通乘法和求逆都为线性运算，其运算复杂度远远小于椭圆曲线上的点乘、Paillier加解密。

Paillier同态加密密文c=rNgm（mod N2），当生成元g取N+1时，gm可以简化成1+mN，进一步密文可以转换为c=rN·（1+mN）（mod N2）。Tp就可以转换成N次乘法运算所需的时间，而N是两个大素数的乘积，N>>1792，因此Tp&gt;>1792Tm。Ti为求逆运算所需时间，求逆运算通过扩展欧几里德算法实现，其计算量与输入的整数大小相关，假设输入的整数为A和模数B，且A<B。扩展欧几里德算法的计算量取决于迭代的次数。每次迭代都需要计算商和余数。在最坏情况下，扩展欧几里德算法的迭代次数不超过log2（A）次。由于SM4协同加解密在线计算阶段的数据大小在0～501，Ti最多为9次除法，因此Tp>>259Ti。由4个方案的效率对比结果（表2）可知，本文方案优于其他方案。

a）本文和文献［17］的对称密码协同加密方案和公钥协同加密方案相比，不需要密钥生成阶段。

b）离线预计算阶段：本文方案中，用户P1执行了16次乘法运算和5次求逆运算，计算时间为16·Tm+5·Ti；用户P2执行了10次乘法运算和3次求逆运算，计算时间为10·Tm+3·Ti。而在文献［17］的方案中，用户P1执行了4次Paillier加/解密计算，计算时间为4·Tp；用户P2执行了4次Paillier加/解密计算，计算时间为4·Tp。文献［6，7］两个公钥协同加密方案均使用了椭圆曲线上的点乘运算和Paillier加/解密。因此本文方案在离线预计算阶段是最优的。

c）在线计算阶段：在本文方案中，用户P1和P2均执行了1 536次乘法运算和256次求逆运算，计算时间都为1536·Tm+256·Ti。文献［17］的方案中，用户P1的计算时间为1536·Tm+256·Ti，用户P2的计算时间为1792·Tm+256·Ti。文献［6］的方案中，用户P1和P2均执行了1次Paillier加/解密计算。文献［7］的方案中，用户P1执行了2次乘法运算和1次求逆运算，计算时间为2·Tm+1·Ti，用户P2执行了3次乘法运算和1次求逆运算，计算时间为3·Tm+1·Ti。文献［22］中，用户P1执行了2次乘法运算、1次点乘运算、1次求逆运算和1次零知识证明，用户P2执行了7次乘法运算、1次点乘运算、3次求逆运算和1次零知识证明。文献［7］所需计算时间最少。

d）全过程：在本文方案中，用户P1的计算时间为1552·Tm+231·Ti，用户P2的计算时间为1546·Tm+259·Ti。因为Tp>>1792Tm，Tp>>259Ti，所以2·Tp>>1552·Tm+231·Ti>1546·Tm+259·Ti。文献［6，7，17，22］中，用户P1和P2的计算时间均大于2·Tp，本文所需计算时间最少，计算效率最高。

4.2 交互次数分析对比

本文方案和文献［17］方案均为SM4协同加解密方案，两方SM4协同加密一次过程中的交互次数对比如表3所示。可以看出，本文方案的交互次数略高于文献［17］，但是在离线预计算阶段，文献［17］需要传输同态加密密文，由同态加密密文c=rNgm（mod N2）可知0<c<N2，而本文传输的信息大小在0～501。因此文献［17］在离线预计算阶段交互时发送的信息量高于本文方案。

4.3 实验验证

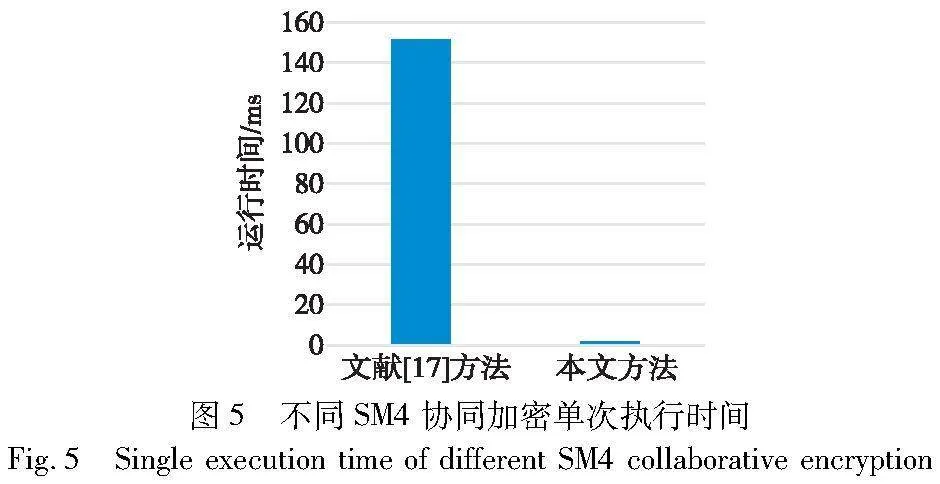
为了验证本文的SM4协同加解密算法相比于文献［17］更加高效，本文在模拟环境下对该算法和文献［17］中的算法进行相同条件下的测试，并对结果进行分析比较。实验环境如表4所示。

在表4的实验环境下，对本文加密方案进行实验验证，并与文献［17］的方案进行相同条件下的测试，从算法的加密执行时间进行分析比较。本文使用国家密码管理局发布的SM4C语言代码来实现SM4协同加解密，使用密码数论库（NTL）实现Paillier同态加密算法，选取Paillier同态加密算法的N为10 bit的3055358447，然后分别选取分割前的明文为0x0123436789abcdeffedcba9876543210，加密密钥为0x012343-6789abcdeffedcba9876543210，分别用本文SM4协同加解密算法和文献［17］中的方法进行100次加密实验，对结果进行整理分析，得到图5所示的不同SM4协同加密单次执行时间对比。

由图5可知，相较于文献［17］，本文方法在SM4协同加密执行时间上具有较大优势。

5 结束语

本文提出了一种基于不经意多项式估值协议的SM4协同加解密方案。在方案的安全性方面，将其规约到S盒协同计算的安全性，并通过基于模拟器的可证明安全方法证明了方案在半诚实敌手模型下是安全的。在方案的性能方面，通过与现有的公钥协同签名方案、SM4协同加解密方案进行对比分析，并进行实验验证。相比之下，本文方案比现有的SM4协同加解密方案更高效，缩短了协同加解密执行的时间。未来将进一步考虑方案性能的优化，同时也将研究其他对称密码算法协同加解密构造方案，并探索本文方案在电子投标文件协同加解密中的应用。

参考文献：

［1］Lindell Y. Secure multiparty computation［J］. Communications of the ACM， 2020，64（1）： 86-96.

［2］Shamir A. How to share a secret［J］. Communications of the ACM， 1979， 22（11）： 612-613.

［3］MacKenzie P， Reiter M K. Two-party generation of DSA signatures［J］. International Journal of Information Security， 2004， 2： 218-239.

［4］Mu Yongheng， Xu Haixia， Li Peili， et al. Secure two-party SM9 signing［J］. Science China Information Sciences， 2020， 63： 1-3.

［5］涂彬彬， 王现方， 张立廷. 两种分布式 SM2/9 算法应用［J］. 密码学报， 2020， 7（6）： 826-838. （Tu Binbin， Wang Xianfang， Zhang Liting. Application of two distributed SM2/9 algorithms［J］. Journal of Cryptography， 2020， 7（6）： 826-838.）

［6］Lindell Y. Fast secure two-party ECDSA signing［J］. Journal of Cryptology， 2021，34： 1-38.

［7］颜萌， 马昌社. 高效的两方ECDSA门限方案［J］. 华南师范大学学报： 自然科学版， 2022，54（4）： 121-128. （Yan Meng， Ma Changshe. An efficient threshold scheme for two-party ECDSA［J］. Journal of South China Normal University： Natural Science Edition， 2022，54（4）： 121-128.）

［8］严都力， 谢敏， 赵艳琦， 等. 抗差分故障攻击的两方协同EdDSA签名方案［J］. 软件学报， 2022， 34（2）： 915-931. （Yan Duli， Xie Min， Zhao Yanqi， et al. A two-party collaborative EdDSA signature scheme against differential fault attacks［J］. Journal of Software， 2023，34（2）： 915-931.）

［9］Doerner J， Kondi Y， Lee E， et al. Secure two-party threshold ECDSA from ECDSA assumptions［C］//Proc of IEEE Symposium on Security and Privacy. Piscataway，NJ： IEEE Press， 2018： 980-997.

［10］文嘉明， 王后珍， 刘金会， 等. Aitps： 基于非对称模格问题的两方协同签名方案［J］. 计算机研究与发展， 2023，60（9）： 1-18. （Wen Jiaming， Wang Houzhen， Liu Jinhui， et al. Aitps： a two-party cooperative signature scheme based on asymmetric modular grid problem［J］. Journal of Computer Research and Development， 2023，60（9）： 1-18.）

［11］Xue Haiyang， Au M H， Xie Xiang， et al. Efficient online-friendly two-party ECDSA signature［C］//Proc of ACM SIGSAC Conference on Computer and Communications Security. New York： ACM Press， 2021： 558-573.

［12］Gennaro R， Goldfeder S， Narayanan A. Threshold-optimal DSA/ECDSA signatures and an application to bitcoin wallet security［C］//Proc of the 14th International Conference on Applied Cryptography and Network Security. Berlin： Springer， 2016： 156-174.

［13］Dttling N， Ghosh S， Nielsen J B， et al. TinyOLE： efficient actively secure two-party computation from oblivious linear function evaluation［C］//Proc of the 24th ACM SIGSAC Conference on Computer and Communications Security. New York： ACM Press， 2017： 2263-2276.

［14］杨博为， 孙达志， 李晓红. 三方不经意多项式求值协议［J］. 计算机工程与设计， 2016， 37（11）： 2934-2938. （Yang Bowei， Sun Dazhi， Li Xiaohong. Three-party oblivious polynomial evaluation protocol［J］. Computer Engineering and Design， 2016，37（11）： 2934-2938.）

［15］Cianciullo L， Ghodosi H. Efficient information theoretic multi-party computation from oblivious linear evaluation［C］//Proc of Internatio-nal Conference on Information Security Theory and Practice. Berlin： Springer， 2018： 78-90.

［16］Cianciullo L， Ghodosi H. Unconditionally secure oblivious polynomial evaluation： a survey and new results［J］. Journal of Computer Science and Technology， 2022，37（2）： 443-458.

［17］杨伊， 何德彪， 文义红， 等. 密钥管理服务系统下的多方协同SM4加/解密方案［J］. 信息网络安全， 2021， 21（8）： 17-25. （Yang Yi， He Debiao， Wen Yihong， et al. Multi-party collaborative SM4 encryption/decryption scheme under key management service system［J］. Information Network Security， 2021，21（8）： 17-25.）

［18］吕克伟， 陈驰. Beaver三元组主动性生成协议研究［J］. 信息网络安全， 2022， 22（12）： 16-24. （Lyu Kewei， Chen Chi. Research on proactive generation protocol of Beaver triples［J］. Information Network Security， 2022，22（12）： 16-24.）

［19］Goldreich O. Foundations of cryptography： basic applications［M］. Cambridge： Cambridge University Press， 2004.

［20］中华人民共和国国家质量监督检验检疫总局. GB/T32907—2016， 信息安全技术SM4分组密码算法［S］. 北京： 中国国家标准化管理委员会， 2016. （General Administration of Quality Supervision， Inspection and Quarantine of the People’s Republic of China. GB/T32907—2016， SM4 block cipher algorithm for information security technology［S］. Beijing： Standardization Administration of the People’s Republic of China， 2016.）

［21］Naor M， Pinkas B. Oblivious transfer with adaptive queries［C］//Proc of the 19th Annual International Cryptology Conference. Berlin： Springer， 1999： 573-590.

［22］彭金辉， 雷宗华， 张志鸿. ECDSA协同签名方案设计与实现［J］. 信息安全研究， 2023， 9（11）： 1120-1130. （Peng Jinhui， Lei Zonghua， Zhang Zhihong. Design and implementation of ECDSA collaborative signature scheme［J］. Journal of Information Security Research， 2023，9（11）： 1120-1130.）