基于改进双档案多目标进化算法的柔性作业车间批量流混排调度

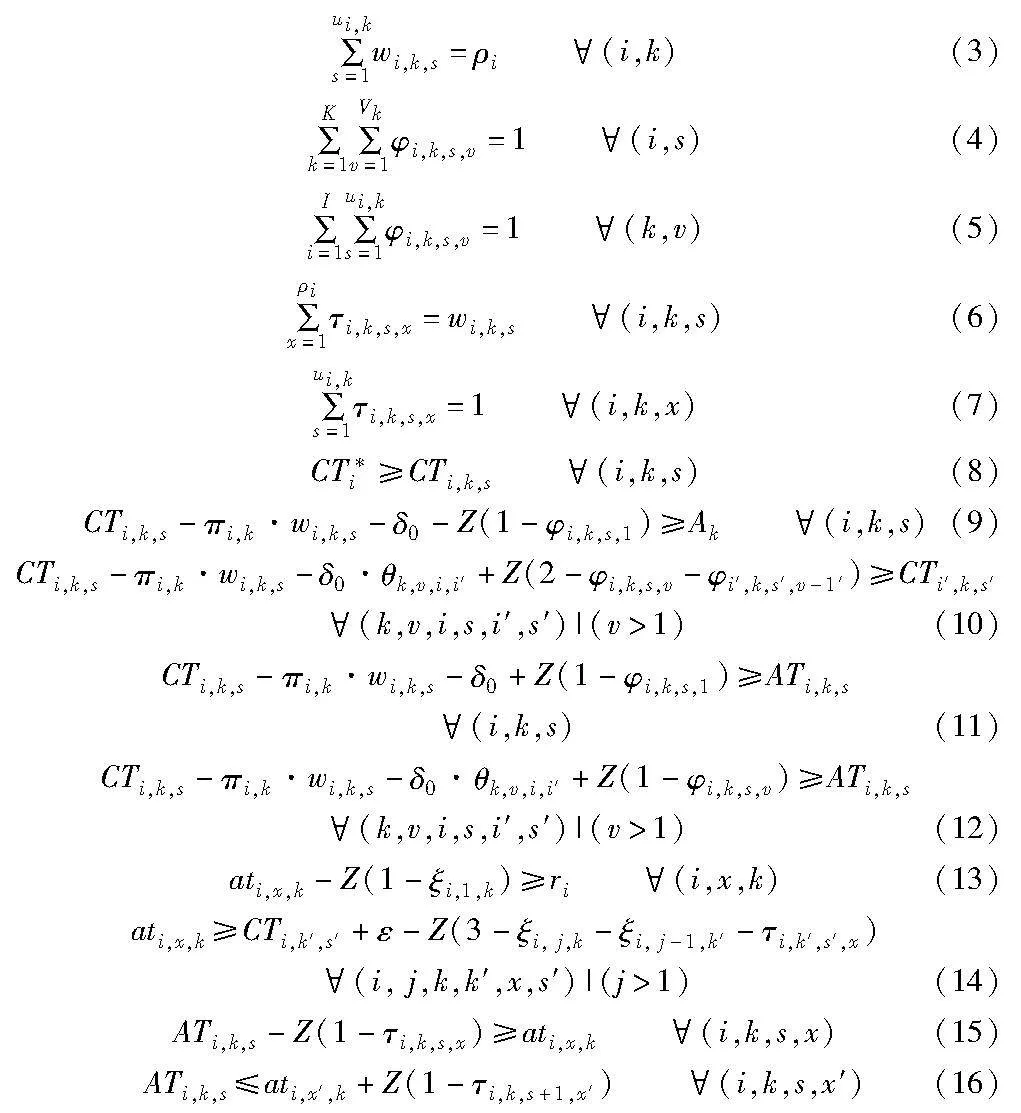
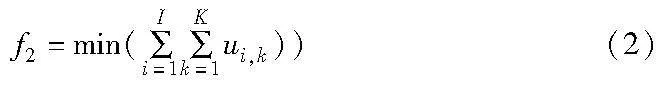
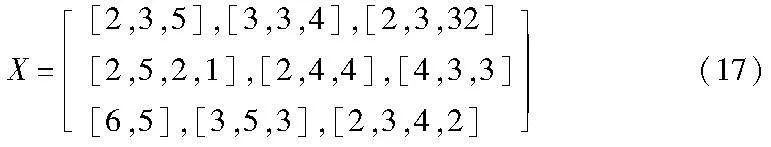
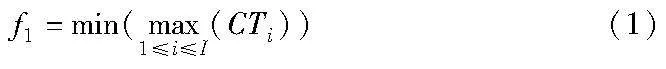
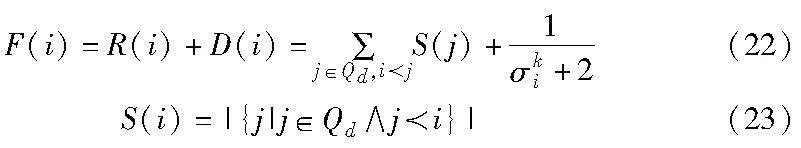
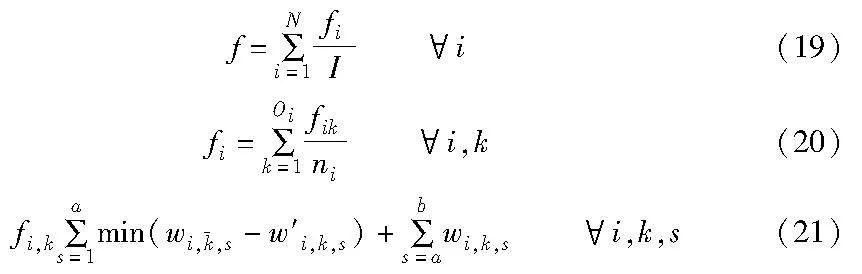
摘 要：针对柔性作业车间批量流调度问题，基于快速换模技术，考虑可变子批划分柔性、子批混排加工柔性、自动换模柔性和物料运输柔性，建立以最小化完工时间和加工子批总数为目标的混排调度优化模型，并提出一种改进双档案多目标进化算法以优化目标函数。基于进化算法框架，设计了基于超体积指标和基于改进帕累托支配的双档案筛选机制，以平衡种群的收敛性和多样性；针对批量流混排调度问题特征，在解码阶段提出正/逆解码和子批拆分左移策略，在邻域探索和全局搜索阶段分别设计子批划分和混排调度的自适应进化算子，以提高算法的全局搜索与局部搜索能力。基于不同规模算例，测试了提出算法与经典多目标算法的性能。实验结果表明，该算法在收敛性与多样性上具有明显优势。

关键词：作业车间；批量流调度；快速换模；多目标进化算法；解码策略

中图分类号：TP29；TH165 文献标志码：A文章编号：1001-3695（2024）06-010-1669-10

doi： 10.19734/j.issn.1001-3695.2023.09.0499

Flexible Job-Shop lot-streaming intermingling scheduling based on

improved two-archive multi-objective evolutionary algorithm

Abstract：Aiming at the flexible Job-Shop lot-streaming scheduling problem， based on the single minute exchange of die （SMED）， this paper established an intermingling scheduling optimization model with objections of minimizing the makespan and the total number of sub-lots， considering the flexibility of sublots splitting and sublots intermingling， automatic changeover and material transportation. Then it proposed an improved two-archive based multi-objective evolutionary algorithm to optimize the objective function. This algorithm adopted the framework of evolutionary algorithm. Based on the framework of evolutionary algorithm， it designed a two-archive based on hypervolume indicator and improved Pareto dominance to balance the convergence and diversity of the population. And according to the characteristics of lot-streaming intermingling problems， it proposed the forward/backward decoding and sub-lot splitting hS8lmMi49X4hwiqGxJYtTQ==left-shift strategies in the decoding stage. In the stages of neighborhood exploration and global search， it designed adaptive evolution operators for lot splitting and sub-lot intermingling schemes respectively to improve the global search and local search capabilities of the algorithm. Based on different scale examples， it tested the performance of the proposed algorithm and the classical multi-objective algorithms. The experimental results show that the algorithm has obvious advantages in convergence and diversity.

Key words：Job-Shop; lot-streaming scheduling; single minute exchange of die; multi-objective evolutionary algorithm; decoding strategy

0 引言

柔性作业车间批量流调度（flexible Job-Shop lot streaming scheduling，FJSLSS）问题作为柔性作业车间调度问题的一个扩展，通过引入批量流技术，将整批工件划分为若干较小的子批，实现分批生产与分批传输，能够有效减少设备空闲时间、缩短完工时间、提高生产效率，并被广泛应用于汽车、航空航天、电子电器、家具等多品种定制化生产制造中［1，2］。FJSLSS问题通常涉及了批量分割和子批排产两个子问题。根据批量分割方法不同，可分为等量分批［1，2］、一致分批［3～5］和可变分批［6～8］。在子批排产阶段，FJSLSS较常采用非混排策略，即同一台机器在加工同一类型工件的各个子批之间不允许其他类型工件子批的插入加工，以最大限度减少换模次数、节约换模时间、缩短机器停工等待时长、提高设备利用率。

非混排调度策略非常适用于换模效率不高的生产系统，并成为批量流调度领域的一个重要研究方向。例如，Huang［1］基于等量分批和子批非混排策略，考虑在制品库存成本、机器空闲成本和子批运输成本等目标，建立了批量流调度优化模型；Daneshamooz等人［2］以柔性作业车间为研究对象，采用等量分批和非混排策略，建立了最小化完工时间的批量流调度混合整数优化模型，并提出了基于变邻域搜索的优化求解算法；Li等人［3］针对柔性装配作业车间分批调度问题，将一致分批策略与非混排策略相结合，建立了混合整数优化模型，并提出了一种改进人工蜂群（ABC）算法进行求解；Defersha等人［4］基于一致分批与非混排策略，以最小化完工时间为目标，建立了柔性作业车间批量流调度混合整数规划模型，并采用改进的遗传算法（IGA）求解；Cheng等人［5］以两阶段柔性装配作业车间为研究对象，考虑完工时间和成本目标，建立了一致子批划分与非混排调度优化模型，并设计了基于列生成的方法；Li［6］集成可变子批划分策略与非混排策略，以最小化完工时间为目标，研究柔性作业车间批量流调度问题，并通过超启发式遗传算法（HHIGA）求解；Bozek等人［7］分别针对可变子批划分和子批非混排两个子问题，以最小化完工时间和子批总数为目标，提出了一种两阶段的分批调度优化方法。

混排调度策略相比于非混排策略具有更大柔性，其允许不同类型工件子批在同一台机器上进行穿插加工，可进一步缩短生产周期、降低在制品库存，但对生产系统的换模效率要求较高［8］。近年来，快速换模技术（single minute exchange of die， SMED）得到了快速发展，并被广泛应用于汽车、食品加工、家用电器、工程机械、医疗器械等领域。SMED采用全自动快速换模系统来缩短换模停机时间，可有效提高机器生产效率［9］。例如，Basri等人［10］在汽车冲压车间引入SMED，以减少冲压工艺模具更换的时间，从而增加总产量；Ribeiro等人［11］将SMED应用于干豆类产品的包装生产中；Ondra［12］在生产车间中引入了SMED和全面生产性维护等策略，以降低机器设备的空闲等待时长并缩短交货期；Emekdar等人［13］将SMED技术应用于丝网印刷行业，并有效减少了生产线停机时间、提高了生产效率。将SMED引入制造车间中，可有效提高换模效率，能够满足多种类型工件子批在同一台机器上的混排生产需求。将SMED引入柔性作业车间中，可有效提高换模效率，能够满足多种类型工件子批在同一台机器上的混合生产需求。因此，本文以多品种、中小批量生产的柔性作业车间为研究对象，基于快速换模技术，将子批混合加工策略引入到批量流调度问题中，以进一步提高生产效率。

柔性作业车间批量流混排调度问题作为柔性作业车间调度问题的一个扩展，也属于典型的NP-hard问题［14］，且其求解难度远大于柔性作业车间调度问题，急需设计一种高效的优化求解算法。双档案优化算法（two-archive algorithm，Two_Arch）［15］是为平衡算法的收敛性和多样性所提出的多目标进化算法，并在多目标、多约束组合优化领域得到了广泛应用。例如，Li等人［16］为平衡解集的收敛性、多样性和可行性，设计了档案间互补的限制性交配选择机制，提出了针对约束多目标优化的双档案进化算法（two-archive evolutionary algorithm for constrained multi-objective optimization，C_TAEA）；Gu等人［17］为求解数据驱动的混合整数优化问题，引入随机森林分类器策略，提出了具有改进双档案的代理辅助多目标优化算法；Srinivasa等人［18］在Two_Arch基础上引入改进MOEA/D中的权重向量自适应策略，提出了基于双档案引导分解的多目标进化算法，以求解多目标多约束问题；Li等人［19］为解决具有更复杂特征的约束多目标问题（constrained multi-objective problem，CMOP）并提高算法优化效率，改进了档案CA的收敛策略，并提出新的DA档案适应度评估方式，提出算法C_TAEA2；Li等人［19］引入推-拉双阶段的搜索策略，以提出双档案辅助推拉进化算法，解决具有复杂不可行区域的多目标多约束问题。

考虑到C_TAEA算法的档案更新方式在解决更复杂的约束条件的问题上表现不佳，尤其是在解决柔性作业车间批量流混排调度这一NP-hard问题上。因此，本文针对柔性作业车间批量流混排调度问题，基于C_TAEA算法框架，设计了基于HV和改进帕累托支配的双档案筛选机制，创新性地提出了一种改进双档案多目标进化算法（two-arch based evolutionary multi-objective algorithm，TB-EMOA）。

1 问题描述及数学模型

柔性作业车间批量流混排调度问题描述为：柔性作业车间中共有K个自动化加工单元（每个加工单元由一台加工设备组成）、一个自动化立体仓库、一个配备有多台AGV的自动化物料运输系统、一套全自动快速换模系统；每个加工单元通过与不同工装模具和其他辅助生产资源的配合，可满足多种类型工件的混线生产需求；现有I种类型的待加工工件，每种工件i （i=1， 2， …，I）的批量大小为ρi；每种工件i的每个零件x （x=1， 2， …，ρi）均需经过ni道工序加工，且每种工件在每道工序上被分配的加工单元k （k=1， 2， …，K）是已知且确定的；基于批量流技术，每种工件在每个加工单元中可被拆分成多个子批进行加工，且同一种工件在不同加工单元中被划分的子批数量ui，k与各子批的批量大小wi，k，s（s=1， 2， …，ui，k）不尽相同（可变子批划分柔性［6］）；每个加工单元在加工同一种工件的任意两个子批之间，允许其他种类工件子批插入加工（子批混排加工柔性［8］）；当同一个加工单元连续加工两个不同种类的工件子批时，基于快速换模技术可自动快速更换模具，以提高多种类型工件混流生产效率（自动换模柔性［21］）；当子批中所有零件均到达加工单元的缓存区且待模具安装（或更换）完成后，子批可开始加工；同一个子批中的所有零件必须被连续加工，不可被其他子批中断；各工件子批在各加工单元之间的流转由AGV完成，当子批结束某工序加工后，可立即被AGV运输至下一个加工单元的缓存区中（各子批的等待运输时间忽略不计，即物料运输柔性［22］）。

为便于对问题进行建模，引入如下符号和变量：

a）符号和参数：

K为加工单元总数；

I为工件总数；

ρi为第i种工件的批量大小；

ri为第i种工件到达车间的时间；

ni为第i种工件的工序总数；

δ0为每个加工单元自动安装（或更换）工装模具的时间；

ε为子批在各加工单元之间的运输时间；

πi，k为第i种工件的单个零件在第k个加工单元中的加工时间；

Ak为第k个加工单元的初始空闲时间；

ξi， j，k为0-1变量，若第i种工件的第j道工序被安排在第k个加工单元上加工，则ξi， j，k=1，反之，ξi， j，k=0。

b）决策变量：

ui，k为整数变量，表示第i种工件在第k个加工单元中被划分的子批数量；

wi，k，s为整数变量，表示第i种工件在第k个加工单元中第s个子批的批量大小（规模）；

Vk为整数变量，表示第k个加工单元所加工的子批总数；

τi，k，s，x为0-1变量，若第i种工件的第x个零件在第k个加工单元中被分配到第s个子批，则τi，k，s，x=1，反之，τi，k，s，x=0；

φi，k，s，v为0-1变量，若第i种工件在第k个加工单元中第s个子批被安排在第v个加工顺序上，则φi，k，s，v=1，反之，φi，k，s，v=0；

θk，v，i，i′为0-1变量，若第k个加工单元所加工的第v个子批与第（v-1）个子批均来自同一种工件（i=i′），则θk，v，i，i′=0，反之，θk，v，i，i′=1；

ATi，k，s为连续变量，表示第i种工件在第k个加工单元中第s个子批的所有零件均到达缓存区的时间；

ati，x，k为连续变量，表示第i种工件的第x个零件到达第k个加工单元缓存区的时间；

CTi，k，s为连续变量，表示第i种工件在第k个加工单元中第s个子批的结束加工时间；

CT*i为连续变量，表示第i种工件的完工时间。

调度目标是基于可变子批划分柔性、子批混排加工柔性、自动换模柔性和物料运输柔性，以最大完工时间最小化、加工子批总数最小化为目标，确定最优的批量流混排调度方案。具体包括：a）确定每种工件i在每个加工单元k中被划分的子批数量ui，k；b）确定每种工件i在每个加工单元k中的每个子批s的批量大小wi，k，s （s=1， 2， …，ui，k）；c）确定各工件子批在各加工单元中的完工时间CTi，k，s。

快速换模作业车间柔性批量流调度优化模型，建立如下：

最大完工时间最小化目标：

加工子批总数最小化目标：

约束条件为

式（3）表示每种工件在每个加工单元中划分的各子批批量总和不得超过该工件的零件总数；式（4）表示任一子批同一时刻只能被一个加工单元加工；式（5）表示每个加工单元在任一时刻只能加工一个子批；式（6）表示被分配到同一个子批中的零件总数不得超过该子批的批量大小；式（7）表示每个零件在每个加工单元中只能被分配在一个子批中；式（8）表示每种工件的完工时间为该工件所有子批的最大完工时间；式（9）（10）表示安装（或更换）模具必须在加工单元空闲时开始，且待模具安装完成后，子批可开始加工；同时，式（10）表示同一个加工单元在加工同一种工件的任意两个子批之间，允许其他种类工件子批插入加工；式（11）（12）表示当且仅当子批在加工单元的缓存区中准备就绪后，该子批可开始加工；同时，式（9）～（12）表示同一个子批中的所有零件必须连续加工，不可被其他子批的零件中断；式（13）（14）表示当子批中所有零件均结束当前工序的加工后，该子批可立即被AGV运输至下一个加工单元的缓存区中；式（15）表示采用可变子批划分策略时，同一个子批中各零件到达同一个加工单元缓存区的时间不尽相同，因此当且仅当该子批中所有零件均到达加工单元缓存区后，该子批才准备就绪；式（16）表示在每个加工单元中，同一种工件的所有零件将按照先到先服务规则依次被划分入各子批中。

2 TB-MOEA算法

所建立的柔性作业车间批量流混排调度优化模型是一个典型的多目标、多变量、多约束 NP-hard 问题。精英档案的保留有助于提高算法的性能［22］，C_TAEA是一种解决约束性问题的多目标进化算法，其通过采取两种不同的档案筛选方式，以平衡算法的收敛性和多样性。在C_TAEA中，档案更新方式采取基于帕累托直接筛选和基于超容量HT指标的档案更新策略，其在解决更复杂的约束条件的问题上表现不佳；在收敛性档案（convergence archive，CA）更新中，其基于帕累托直接筛选的机制总是更倾向于可行的解，从而导致其仅在局部区域进行探索，而无法完整探索解空间，且基于超容量HT指标的多样性归档（diversity archive，DA），处理具有更复杂特征的CMOP时，可能会远离真实帕累托前沿。

基于强帕累托支配算法［23］，采取帕累托支配和邻近法相结合的档案修建方式，在求解多目标多约束问题时具有良好的性能。因此，在C_TAEA算法框架上，设计了基于HV指标和基于改进帕累托支配的双档案筛选机制，提出了TB-MOEA算法。算法框架如图1所示。结合柔性作业车间批量流调度问题特征，对算法关键步骤（编码方式、种群初始化、解码策略、档案修建、局部和全局搜索等）进行了详细设计。

2.1 编码

针对柔性作业车间批量流调度问题，需分别对可变子批划分（BS）和子批混排调度方案（BP）两个子问题进行编码。采用两级编码Chrome=［X， Y］，其中X表示可变子批划分， Y表示子批混排调度方案。

2.1.1 可变子批划分X

采用二维不规则数组X=［aij］I×N表示可变子批划分编码，其中aij=［wij1，wij2，…，wijs，…，wijui， j］，表示第i个工件在第j道工序上划分的分批方案；wijs为第i个工件在第j道工序上的第s个子批的批量大小；uij为第i个工件在第j道工序上划分的子批总数。以式（17）为例，其中a21=［w211，w212，w212］=［4，3，3］，即第2个工件所需要加工的零件总数为10，在第1道工序被分为3个子批进行加工，子批大小分别为4、3和3。

2.1.2 子批混排调度方案Y

采用一维数组Y=［aj］N表示子批混排调度编码，其中每一个元素aj=（i， j）表示工件i的第j道工序；Y中每个元素aj=（i， j）重复出现的次数，则表示该工件i在第j道工序上拆分的子批数量。以图2的染色体编码为例，第一次出现的（3，1）表示第3个工件第一道工序上的第1个子批；第二次出现的（3，1）表示第3个工件第一道工序上的第2个子批。

2.2 初始化

为促进目标空间收敛并保证解的多样性，分别针对工件分批方案和子批混排调度方案，设计了初始种群生成规则。

a）采用文献［24］中的工件分批方案初始化方法，具体为：（a）平均分批；（b）随机分批；（c）均匀划分后引入随机量以改变分批。

b）采用经典调度规则［25］生成子批混排调度方案：（a）最多工序剩余的子批最先开始加工；（b）最长剩余加工时间的子批最先开始加工；（c）随机生成子批混排调度方案。种群生成比例设置为1∶1∶8。

2.3 解码

解码过程就是在算法的编码基础上进行信息读取，以生成调度表。针对柔性作业车间批量流调度问题特征，设计了基于正序/逆序解码+子批拆分左移+子批合并的解码策略，以增强对个体解在解空间上的邻域探索。

2.3.1 正解码

传统调度问题的解码方式较常采用正解码。在正解码中，解码顺序为在Y染色体依次读取子批混排调度方案 → X染色体上读取该子批的零件数目 → 在工件加工信息上读取单一零件的加工时间以获取总子批的加工时间 → 获取此前机器加工信息 → 在机器上安排该子批加工。

2.3.2 逆解码

正解码和逆解码的不同点在于“X染色体上读取子批加工零件数目”这一环节，逆序解码策略需要将现有可变子批划分方案X通过逆序操作来生成一个新的可变子批划分方案。该策略的核心思想就是针对每个工件的每道工序所对应的可变子批划分信息，在加工顺序不发生改变的情况下，通过逆序可变子批划分信息的方式获取一个与当前染色体相似度较高的解，即在染色体上，将aij=［wij1，wij2，…，wijs，…，wijui， j］逆序后获得aij=［wijui， j，…，wijs，…，wij2，wij1］。以式（18）中的染色体编码为例，将原染色体SSori通过逆序操作变成SSrev。

2.3.3 子批拆分左移策略

将子批拆分与左移插空策略相结合，通过将某子批中的部分零件左移来提前加工，同时减少机器上的空闲时间以优化子批的最大完工时间。拆分左移的伪代码如算法1所示。图3中（a）为子批拆分左移策略的单一机器图例，（b）为实际调度表案例。在图（b）中，通过将原本安排在M3上加工的工件3的第二道工序的一个子批，拆分为两个子批，并将一个子批左移至可加工的时间点，可显著缩短最大完工时间。

2.3.4 子批合并策略

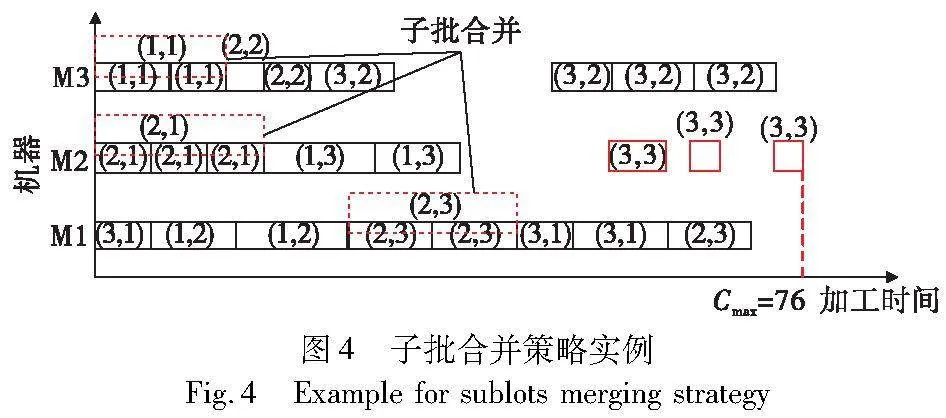
保证档案筛选中的个体是本次迭代过程的更优解，算法引入子批合并策略。这一策略的核心思想是：在不影响任一工件的任意零件在其对应机器上的加工时间前提下，将两个子批合并形成一个新的子批，新子批的大小等于原两子批大小之和。子批合并策略伪代码如算法2所示，实例如图4所示。

算法1 子批拆分左移策略

算法2 子批合并策略

2.4 档案修建

2.4.1 相似度筛选

在探索解空间以获取最优帕累托前沿过程中，种群中存在部分编码不同而目标值相同的个体。如图5所示，任意序列①～⑤中所选中的子批批次数量改变和子批加工顺序互换都不会改变目标值。当这些相似度高的个体适应度值较好时，这部分个体将被保留下来，从而降低种群多样性、导致算法陷入局部最优。因此，在TB-MOEA算法中引入了相似度筛选，以避免过多近似解进入双档案中。在相似度筛选中，考虑到算法的多样性需求及问题的目标值仅为两个，因此仅对目标值一致的目标进行筛选。在获取相似值后，对相似值大于0.95的解进行随机保留，即保留一个个体解，以避免其占据后续迭代种群的位置。通过计算个体之间每个工件的对应工序的分批信息的绝对距离得到相似度筛选的适应值f，其计算公式如下：

其中： fi表示工件i的分批方案相似度； fi，k表示工件i在加工单元k上的子批分批方案相似度；wi，k，s和w′i，k，s代表需要进行相似度计算的两个子批分批方案排序列表之间的绝对距离。

2.4.2 双档案机制

TB-MOEA算法采用双档案筛选机制来平衡算法的收敛性和多样性。该筛选机制核心思想是通过不同的更新机制分别更新CA和DA来平衡算法的收敛性和多样性。两种档案的更新策略步骤如下：

1）档案CA的更新策略（档案上限设定为N，种群数量为M）

a）迭代的新种群POP与档案CA合并形成QC。

b）通过快速非主导排序将QC划分为多个子集。

c）按分层顺序依次取出子集，并获取子集个体数n。

d）若子集个体数（n+CA）现有个体数s小于CA上限N，返回步骤c），否则进行步骤e）。

e）计算该子集每个个体的独立超体积贡献值，并逐个删除适应度最低的个体，即每次仅删除一个解，直到（n+CA）现有个体数等于CA上限。

2）档案DA的更新策略

a）将迭代的新种群POP与档案DA合并形成QD；

b）获取QD的个体数L，获取需要保留的随机解数量RN=min（25，（M-N）/2）；

c）通过式（22）（23）计算适应度值，保留适应度值较小的对应解，保留数量为A=max（25， （3N-M）/2），随后通过随机筛选的方式，在剩余解集中抽取个体数为RN，依次来有效确保算法的多样性。

其中：F（i）为适应值；R（i）和D（i）分别为支配个体i的解所支配的个体数和k-邻近法所求的种群密度值；S（i）为工件i所支配解的数量。

2.5 邻域与全局搜索

为找到距离真实帕累托前沿最近且分布性好的帕累托前沿，对TB-MOEA算法的邻域和全局搜索作出了改进。在邻域搜索部分，考虑到收敛性需求，邻域搜索仅在档案CA上展开；全局搜索在集合［CA， DA］上展开，同时在全局搜索上采用了改进的交叉和变异算子，以提高种群多样性并避免迭代过程陷入局部最优。

2.5.1 邻域探索

在TB-MOEA算法中，分别针对可变子批划分方案和子批混排调度两部分设计了算子。在可变子批划分方案上，通过所设计的自适应寻优算子在档案CA上抽取亲代以生成后代；在子批混排调度方案上，通过基于关键链的算子探寻邻域解，具体如下：

a）针对可变子批划分方案的自适应寻优变异算子。

通过改进文献［26］中最优个体的变异方式，生成自适应寻优算子，具体如下：首先需要通过随机抽取的方式，在档案CA中抽取本次的亲代F；随后在档案CA中获取关于F的支配解集和非支配解集，在支配解集和非支配解集中，各抽取一个解作为优解和劣解，对比优、劣解的分批方案，获取亲代中与劣解相同或相似的某一工件某一工序的可变子批划分方案，将优解中的方案替代原亲代方案，生成新解，伪代码如算法3所示。

算法3 自适应寻优变异算子

b）针对子批混排调度方案的变异算子。

基于关键链的邻域搜索策略，可有效缩短车间调度问题的工件最大完工时间。关键链是从第一个开始加工的子批开始到最后一个完成加工子批的最长路径；关键链上的操作被定义为关键工序；同一机器上前后多个关键工序合在一起被称为关键块。基于关键链子批混排调度变异算子的步骤如下：首先在调度表上获取一条关键链；然后找出该关键链上的所有关键块；最后随机抽取若干关键块，并将其关键工序互换，以生成新的子批混排调度方案。如图6所示，在图（a）中获取关键链，通过改变机器M3上的关键块中关键工序的加工顺序，就可得到图（b）中新的调度图，并有效减少了工件的最大完工时间。

2.5.2 全局开发

针对柔性作业车间批量流调度问题特征，分别针对可变子批划分方案和子批混排调度两部分设计了算子，以提高在调度问题上的算子适用性，具体如下：

a）针对可变子批划分的随机变异算子。

变异算子的步骤如下：

（a）在档案CA和档案DA的档案合集上，随机抽取亲代F；

（b）随机抽取亲代F上某一工件的某一工序的可变子批划分信息w；

（c）在（1， N-length（w））上随机抽取一个值，并将该值作为该可变子批划分上随机抽取的一个子批的新大小，并获取前后改变的大小差值，d=old-new；

（d）生成随机数GS=random（0，1），若GS小于0.5，转到步骤（e），否则转到步骤（f）；

（e）将差值均摊给其他子批，并在差值为负数时，子批大小为1的子批将不会减少子批大小，即保证子批数量不发生改变，转到步骤（g）；

（f）在差值为正时，将差值重新生成一个新的子批；差值为负数的时候，将差值均摊给其他子批，但允许子批大小为0，当子批大小为0的时候将减少子批数量；

（g）获取变异的子批信息，取代亲代原片段以生成子代。

b）针对子批混排调度方案的进化算子。

采用进化算法中较为常用的进化算子［16］，即反演突变算子和子路径交叉算子。其操作详解如下：

（a）反演突变算子：通过随机抽取染色体片段，对该片段进行逆序编码以生成新解；然后考虑加工工序顺序约束，对非可行染色体作修正。具体如图7所示。

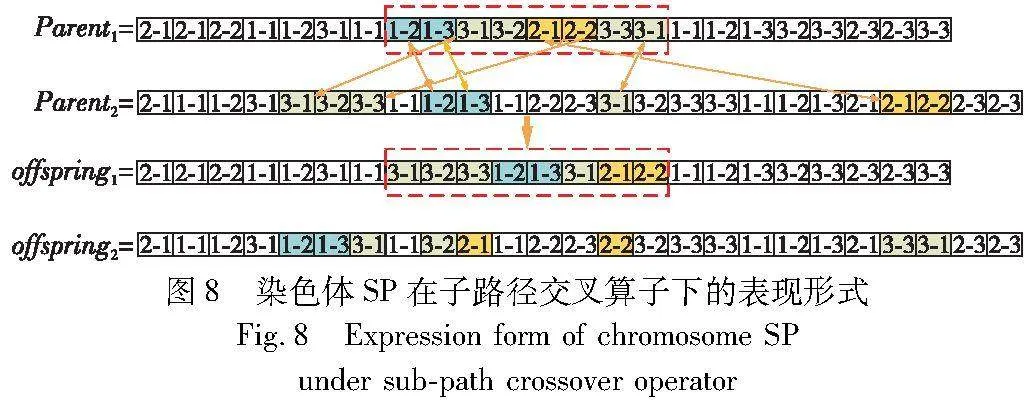
（b）路径交叉算子：在档案CA和档案DA中各抽取一个解作为亲代F1和F2，并在亲代上F1选择一组基因片段；然后，在亲代F2上寻找到亲代F1上该片段每个元素所对应的位置，并将亲代F1和F2中所选中位置上的元素进行替换，以完成交叉操作。具体操作以图8为例。

3 实验

为了确保模型的可靠性，本文对模型进行了有效性验证。最终模型在输入输出关系、稳定性等方面都得到了较好的验证。

算法采用Python编程实现，测试计算机参数：CPU为AMD Ryzen 7 5800H 3.2 GHz，内存为16 GB。为测试算法性能，设计了18个不同规模（I×O×M）算例。其中，工件数I的范围为{7，10，15}；工序数设定为O={6，8}；机器数为M={8，10，15，20}。其余参数如表1所示。

3.1 参数设定

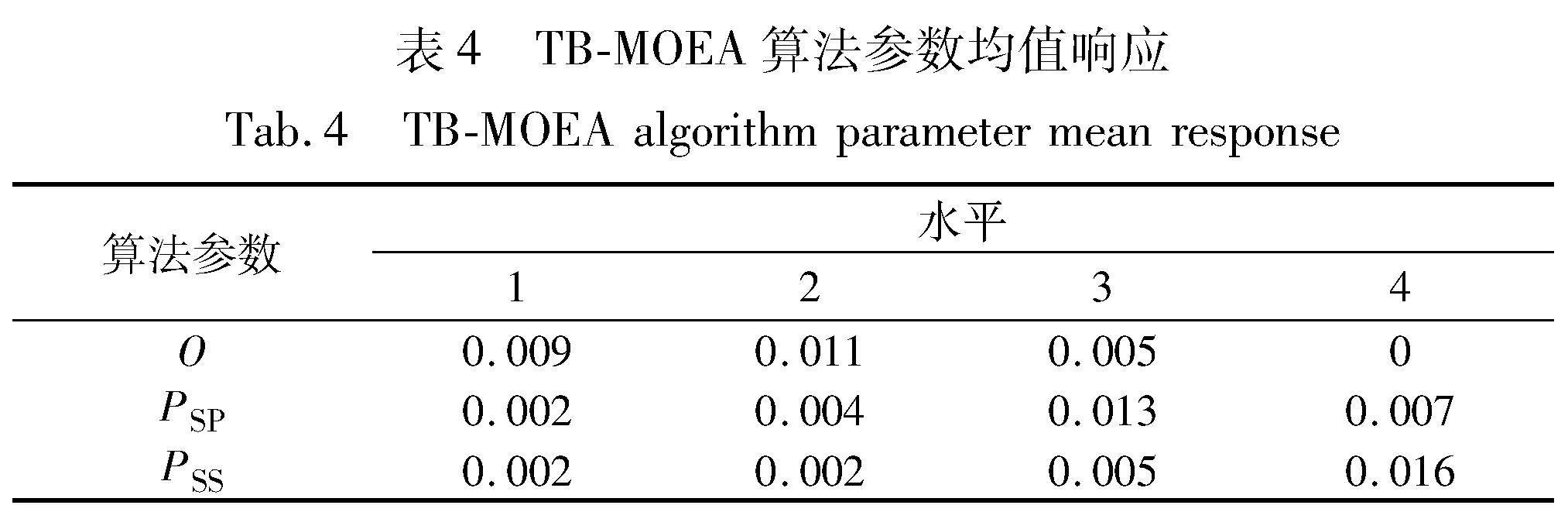
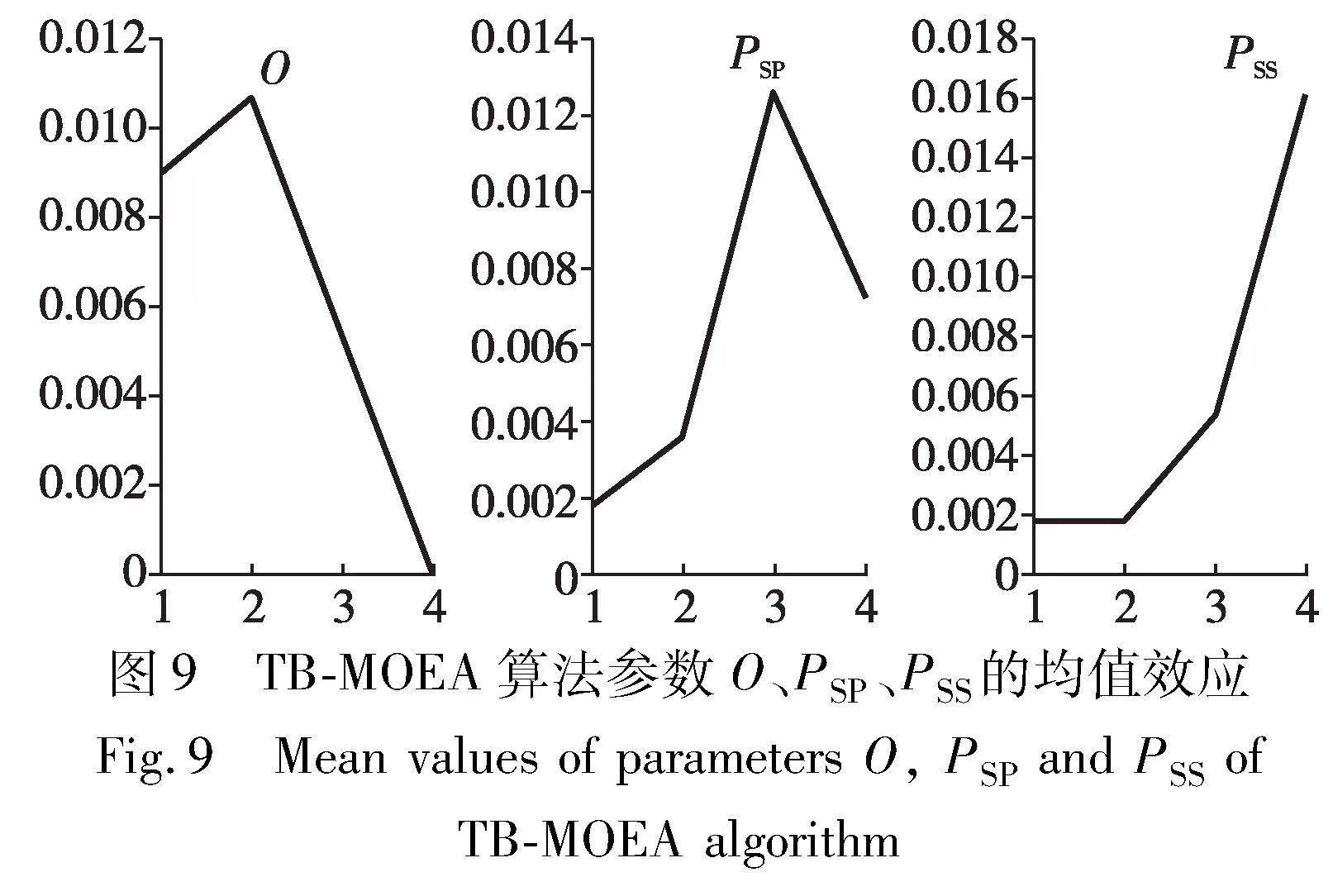
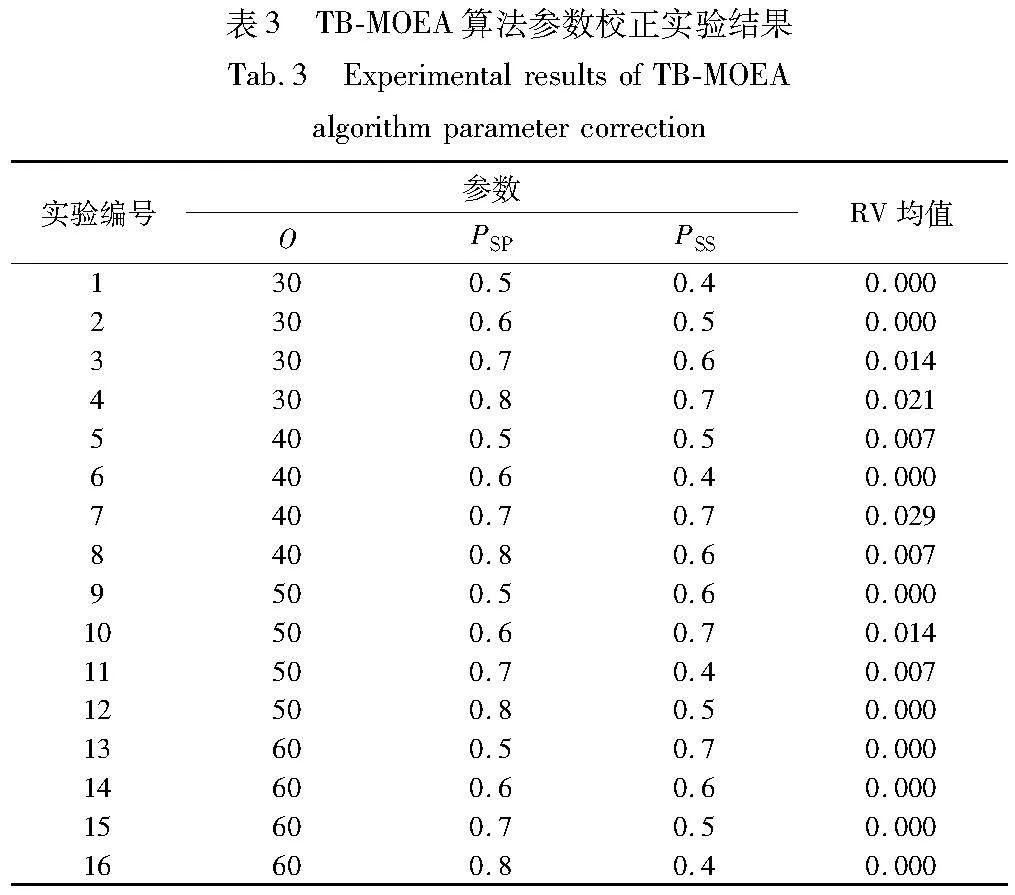
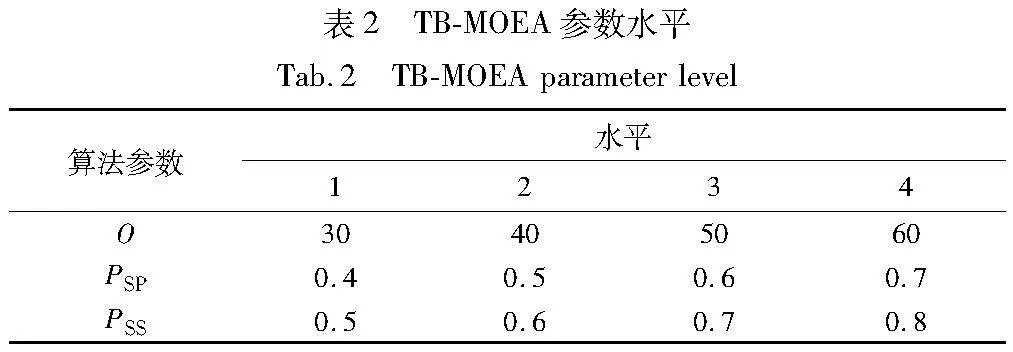
采用全因素实验（DOE）设计确定TB-MOEA算法最优参数。TB-MOEA算法的关键参数包括邻域解数量O、全局搜索中加工顺序编码概率PSP和可变子批划分概率PSS。每个参数设置4个水平，如表2所示。选取案例L06作为测试对象，以总迭代次数50作为终止条件，在每种参数组合下运行算法十次，总运行次数为4×4×10=160次，记录每次运行后获得的非支配解集。在所有组合被测试后，获得一个最终的非支配解集，并将其他每种组合所获得的非支配解集占最终非支配解集的比例作为响应值（response variable， RV）。RV越大，表示其对应的参数组合下的算法性能更优。正交实验结果如表3所示。表4表示TB-MOEA算法参数的均值响应。图9表示TB-MOEA算法的参数水平，由图9可知，TB-MOEA算法最优参数为：邻域解数量O=40，全局搜索中加工顺序编码概率PSP=0.6，可变子批划分概率PSS=0.8。

3.2 策略有效性验证

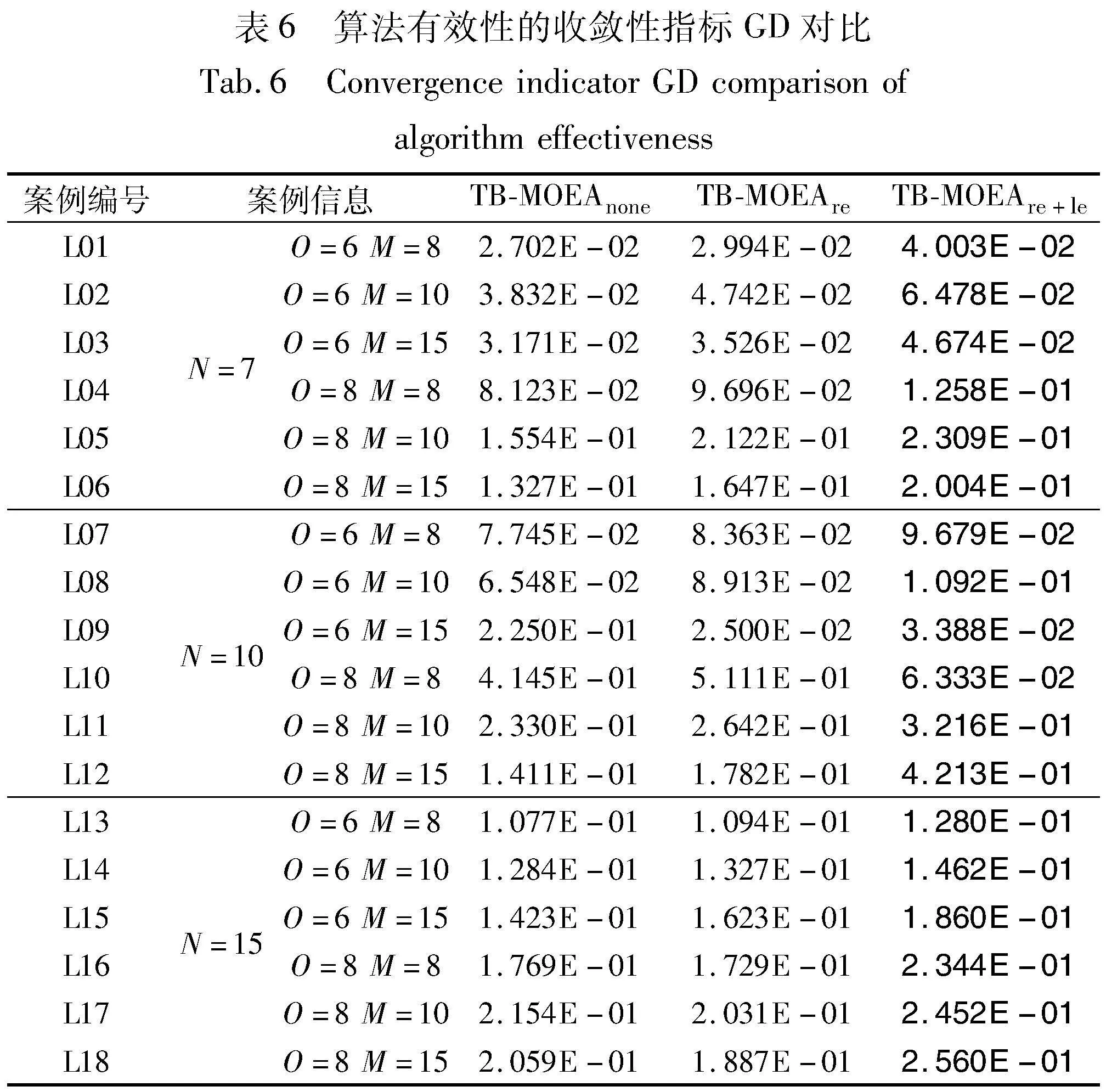
为验证所设计的正/逆解码和左移拆分策略的有效性，在设计的算法框架等不改变的情况下，分为以下三种：a）只采用正序解码的TB-MOEAnone；b）采用正序+逆序解码策略的TB-MOEAre；c）采用正序解码+逆序解码+左移拆分策略的TB-MOEAre+le。每种算法在不同规模算例上分别运行十次，并采用多样性指标Δ（S，P）、收敛性指标GD（generational distance，世代距离） 和综合指标HV（hypervolume，超体积指标） 来对算法性能进行评价。其中，多样性指标Δ（S，P）越小代表算法多样性越好，指标GD值越小代表算法收敛性越好，指标HV越大表示算法综合性能越好。

实验结果如表5～7所示，其中加粗部分表示算法所获得的指标更好，即该组对应获得的帕累托前沿具有更好的收敛性和多样性。

由表5～7可知，TB-MOEAre+le在18组规模算例中均获得了多样性指标Δ（S，P）、收敛性指标GD和综合指标HV的最优值；TB-MOEAre在所有算例上的HV值均优于TB-MOEAnone，在15组算例上取得更优的Δ（S，P）值，在14组算例上GD值表现更优。TB-MOEAnone在三个性能指标上的表现最不理想。从指标数值结果来看，TB-MOEAnone、TB-MOEAre、TB-MOEAre+le算法的Δ（S，P）均值分别为7.131E-01、7.124E-01和5.380E-01，GD均值分别为1.452E-01、1.230E-01和8.724E-02，HV均值为1.113E-01、1.072E-01和1.722E-01，说明算法TB-MOEAre+le在收敛性、多样性和综合性能上均优于TB-MOEAnone和TB-MOEAre。为直观地证实结论，通过置信度为95%的置信区间图来展示。以三者的HV区间图为例，如图10所示，TB-MOEAnone与TB-MOEAre重叠部分较大，且置信区间上下限相近，但都明显低于TB-MOEAre+le，说明TB-MOEAre+le在综合性能上要明显优于TB-MOEAre和TB-MOEAnone。TB-MOEAre+le相比于TB-MOEAnone和TB-MOEAre的优势在于：a）通过正/逆解码策略有效保证了种群多样性，并提高了算法的全局搜索能力；b）左移拆分策略加强算法局部搜索能力，促进了种群收敛。

3.3 算法性能对比

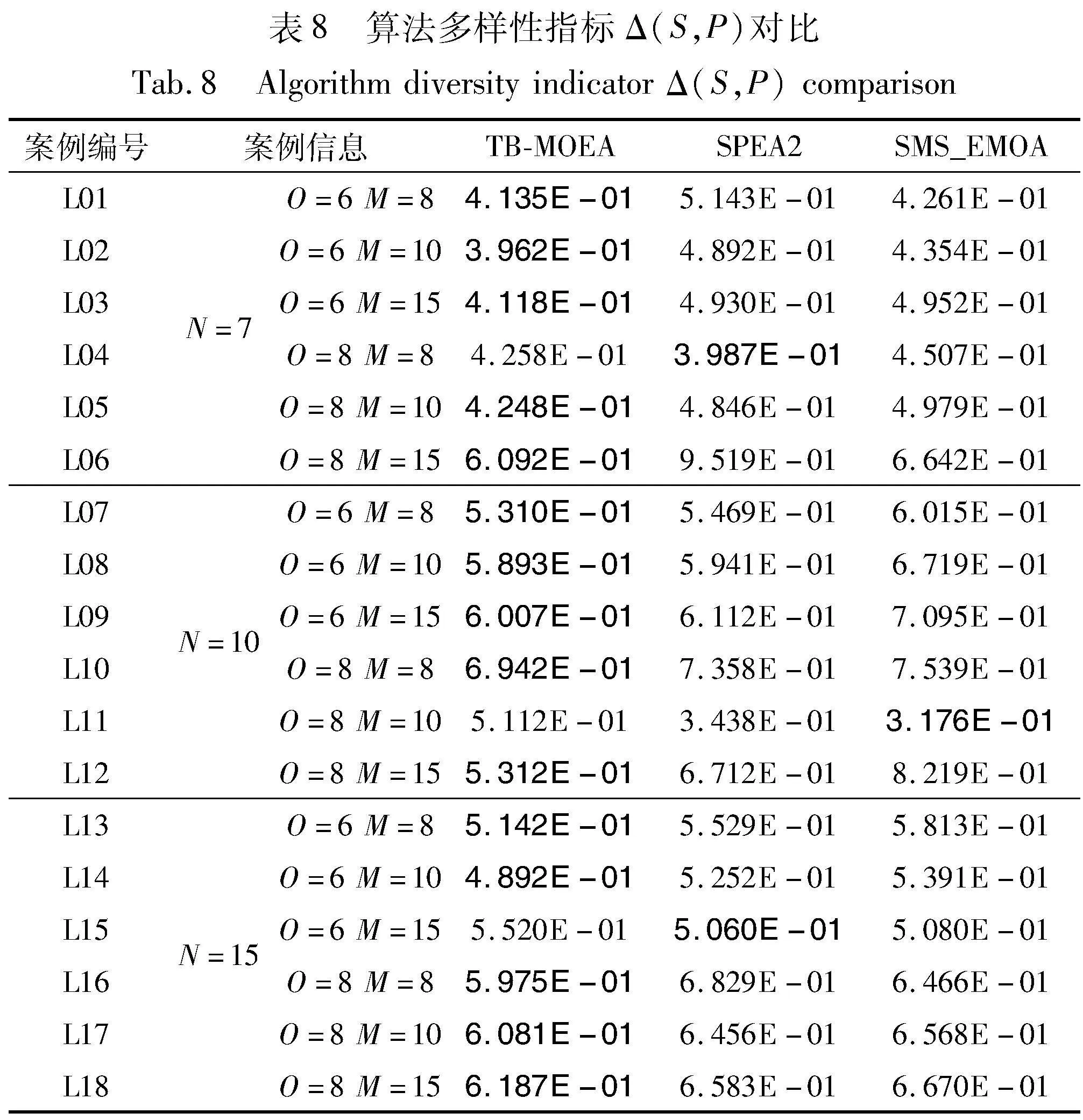
为测试TB-MOEA 算法在柔性作业车间批量流调度问题上的有效性，将其与SPEA2、SMS-EMOA进行对比测试。其中，SPEA2、SMS-EMOA的种群大小设置与TB-MOEA 算法相同，所有算法均共用初始化、解码、相似度筛选等策略。此外，在迭代阶段，SPEA2、SMS-EMOA算法采用2.5节所提出的邻域搜索和全局开发思想进行解空间探索，但在亲代选择方式上因算法框架不同而采取轮盘赌的方式。每种算法在不同规模算例上分别运行十次，得到的算法性能指标Δ（S，P）、GD、HV平均值如表8～10所示，其中加粗部分表示算法所获得的指标更优。

在表8中，TB-MOEA在15个算例上获取多样性指标Δ（S，P）的最优值，SPEA2和SMS-EMOA分别取得了1、2个算例上的指标Δ（S，P）的最优值，由此初步推断TB-MOEA在多样性上优于SPEA2和SMS-EMOA算法。TB-MOEA、SPEA2和SMS-EMOA的多样性指标Δ（S，P）平均值分别为5.380E-01、5.563E-01和5.459E-01。由于TB-MOEA的平均Δ（S，P）值小于SMS-EMOA，同时SMS-EMOA的平均Δ（S，P）值小于SPEA2，通过置信区间可以得出结论，TB-MOEA在多样性上较优于SPEA2和SMS-EMOA。

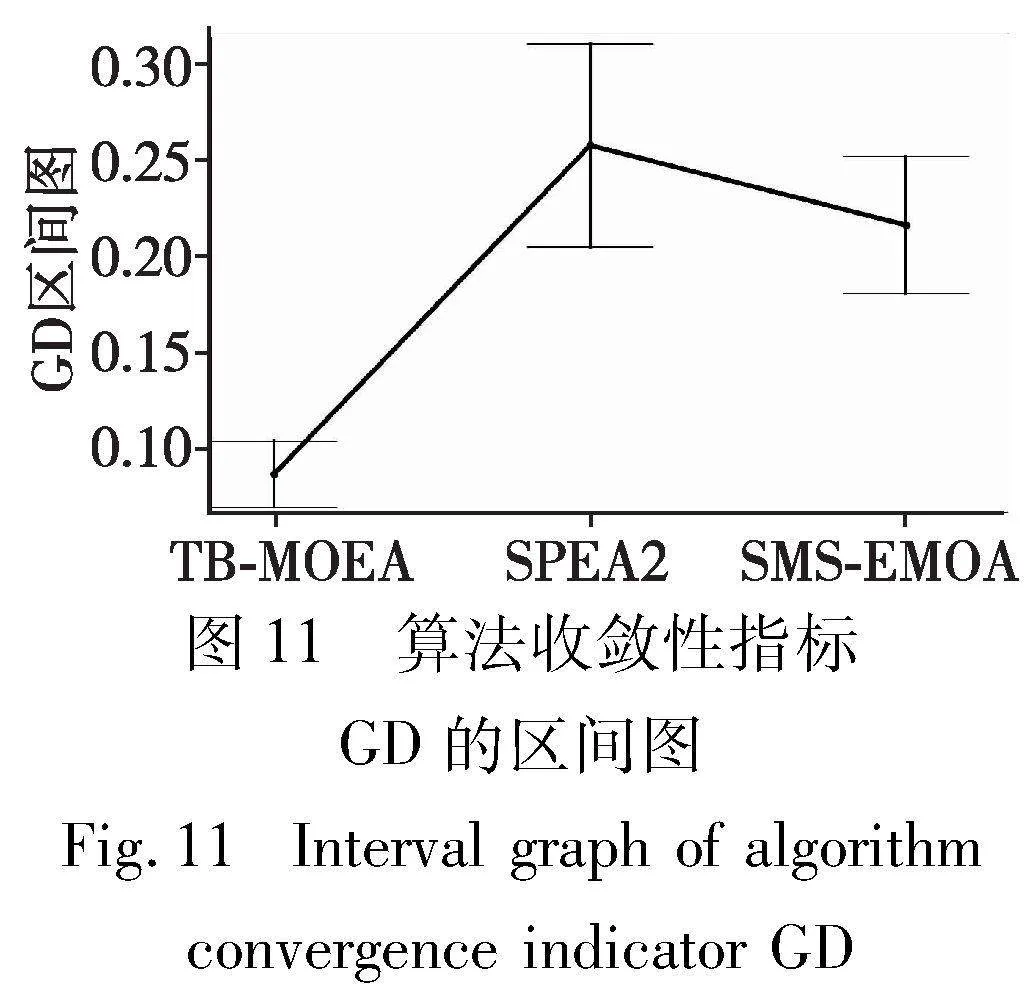
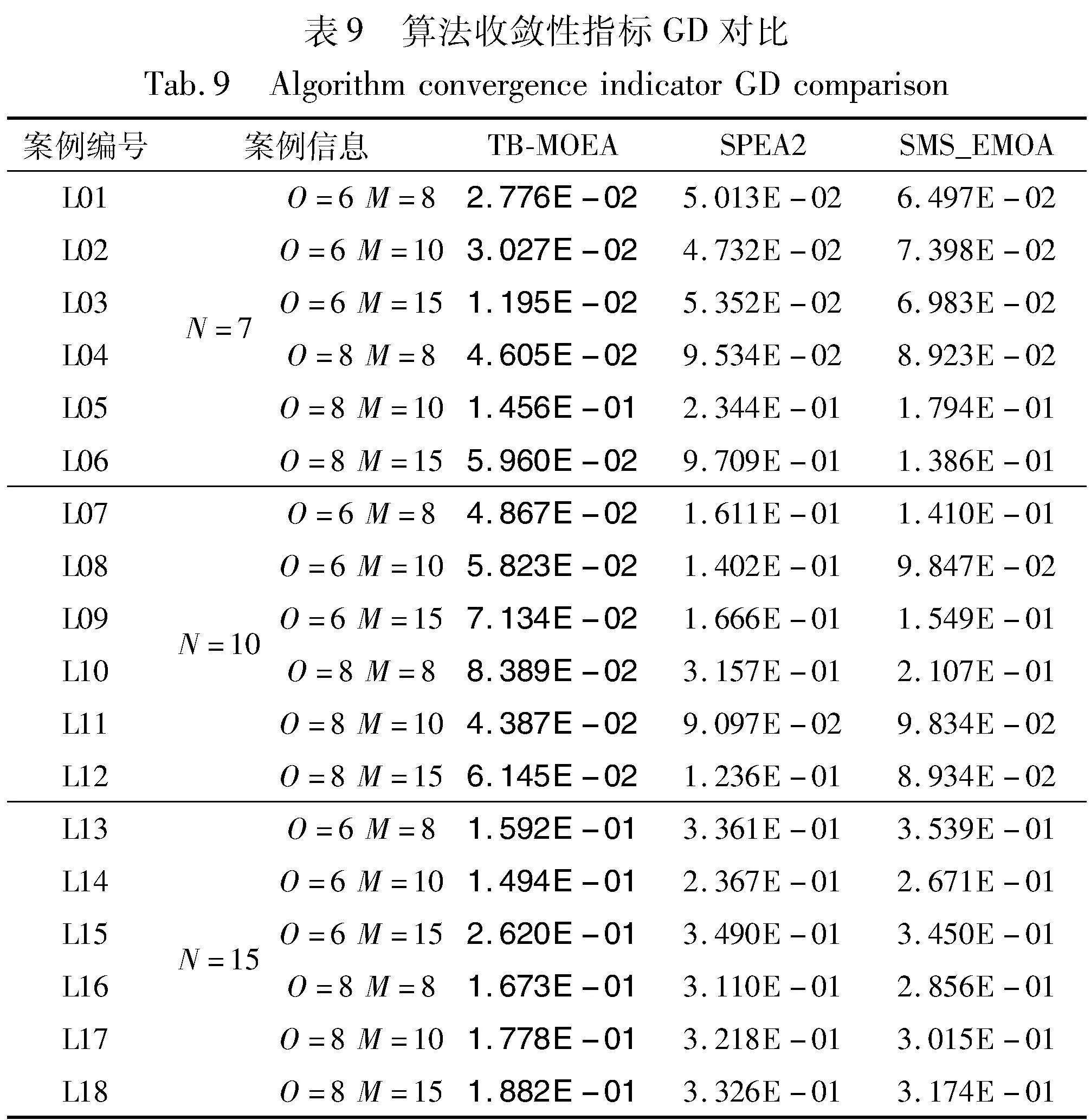
在表9中，TB-MOEA在全部18个算例上获取收敛性指标GD的最优值，由此说明在收敛性上，TB-MOEA优于SPEA2和SMS-EMOA。对收敛性指标求平均值，可得TB-MOEA、SPEA2和SMS-EMOA的GD平均值分别为8.724E-02、2.580E-01和2.166E-01。由于TB-MOEA的平均GD值小于SMS-EMOA，SMS-EMOA的平均GD值小于SPEA2，所以在收敛性上TB-MOEA>SMS-EMOA>SPEA2。通过执行一个双边t检验以获得其95%的置信区间图，如图11所示。可以看出，TB-MOEA在收敛性上显著优于SPEA2和SMS-EMOA，同时SMS-EMOA的收敛性优于SPEA2。

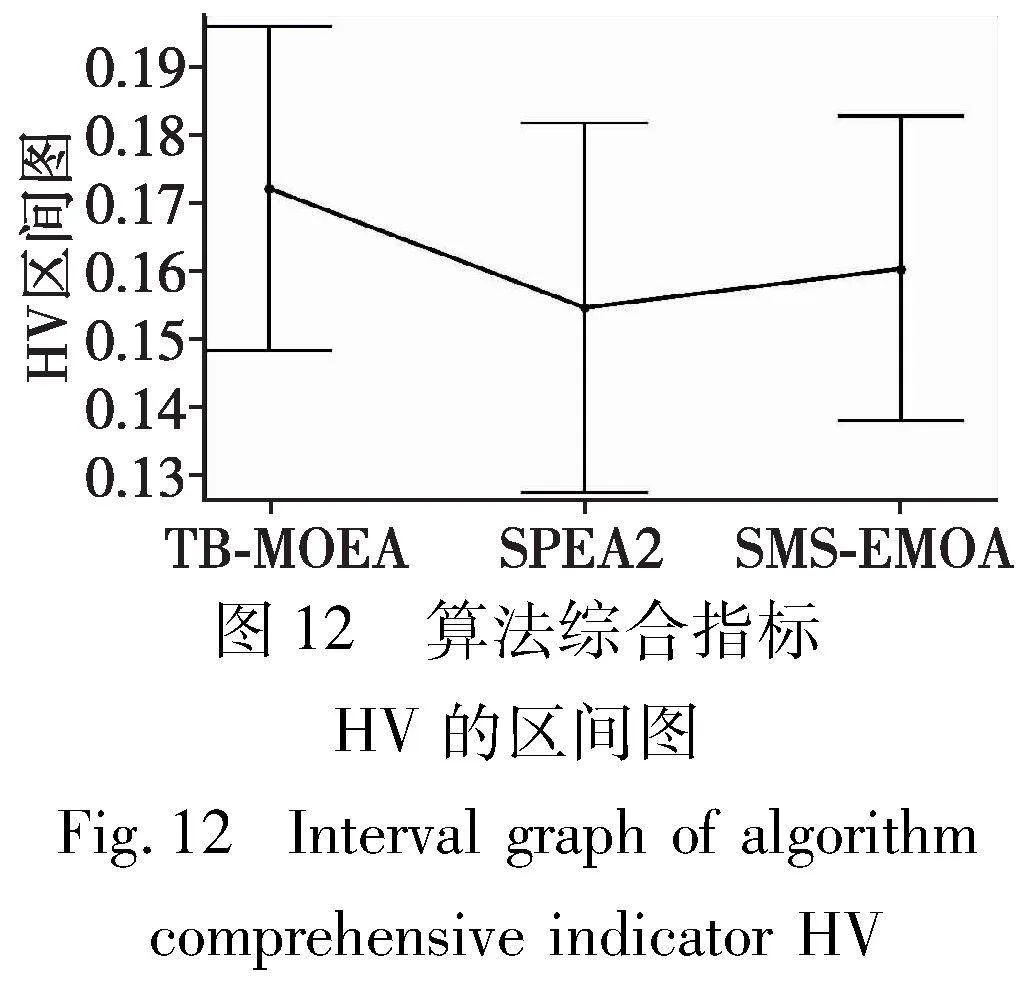
在表10中，TB-MOEA在全部18个算例上获取综合性指标HV的最优值，可初步得到在综合性上TB-MOEA优于SPEA2和SMS-EMOA两个算法。TB-MOEA、SPEA2和SMS-EMOA的HV平均值分别为1.722E-01、1.547E-01和1.604E-01。可以得到TB-MOEA的平均HV值大于SMS-EMOA，SMS-EMOA大于SPEA2。进一步推断综合性，TB-MOEA> SMS-EMOA > SPEA2。为验证这一结论，通过执行一个双边t检验以获得其95%的置信区间图，如图12所示。可以看出，TB-MOEA所占区间整体上较优于SMS-EMOA和SPEA2，可得到TB-MOEA要较优于SPEA2和SMS-EMOA。由此可以得出结论，TB-MOEA在综合性上较优于SPEA2和SMS-EMOA。

图13展示了柔性作业车间在批量流混排情况下的甘特图，图14展示了三种算法在18种不同算例下的帕累托前沿。由图14可以明显看出，TB-EMOA算法求解柔性分批调度问题所获得的前沿明显优于SPEA2和SMS-EMOA，所获取的帕累托前沿大多都能支配SPEA2和SMS-EMOA所获取的前沿中的个体解。此结果说明，TB-MOEA算法在求解多目标批量流调度问题上具有优越性。

综上所述，TB-MOEA在多样性、收敛性和综合性上均优于SPEA2和SMS-EMOA，算法对比过程中共享大部分代码，仅在算法框架上有所不同，其TB-MOEA算法性能更好的主要原因在于：通过能平衡算法的收敛性和多样性的双档案机制，使用两个外部精英档案分别专注于算法多样性和收敛性，来保障种群迭代过程中不至于陷入局部最优。

4 结束语

针对柔性作业车间批量流调度问题，集成可变子批划分柔性、子批混排加工柔性、自动换模柔性和物料运输柔性，以最大完工时间最小化、加工子批总数最小化为目标，建立了批量流混排调度混合整数线性规划模型。在C-TAEA算法框架基础上，设计了基于HV和改进帕累托支配的双档案筛选机制，并提出了一种改进双档案多目标进化算法；结合作业车间柔性批量流调度问题特征，设计了基于正/逆解码和左移拆分策略的解码，设计了邻域探索和全局开发适应性算子，以提高算法的全局搜索与局部搜索性能。选取不同规模算例，验证了所设计解码策略的有效性，实验结果表明，左移拆分策略对算法的多样性和收敛性能有明显提升，正/逆序解码策略能有效提高算法的收敛性能；同时，在共享编码、解码、迭代策略的情况下，测试了TB-MOEA与经典多目标算法SPEA2、SMS-EMOA的算法框架在不同规模算例下的求解性能，结果表明，TB-MOEA在解集多样性、收敛性和综合性上均具有明显优势，由此说明双档案筛选机制所采取的使用两个精英外部档案保留种群的方式，有效地促进了算法在多样性和收敛上的平衡，从而通过算法能有效获得调度问题的最优帕累托前沿。后续研究可将批量流混排调度方法扩展到更为复杂的生产系统中（如动态生产环境），并添加更多约束以贴近实际生产，同时进一步提高算法的求解性能。

参考文献：

［1］Huang Ronghua. Multi-objective Job-Shop scheduling with lot-splitting production ［J］. International Journal of Production Econo-mics，2010，124（1）：206-213.

［2］Daneshamooz F，Fattahi P，Hosseini S M H. Scheduling in a flexible Job-Shop followed by some parallel assembly stations considering lot streaming［J］. Engineering Optimization，2022，54（4）： 614-633.

［3］Li Xiulin，Lu Jiansan，Yang Chenxi，et al. Research of flexible assembly Job-Shop batch-scheduling problem based on improved artificial bee colony［J］. Frontiers in Bioengineering and Biotechnology，2020，10：909548.

［4］Defersha F M，Movahed S B. Linear programming assisted （not embedded） genetic algorithm for flexible Job-Shop scheduling with lot streaming［J］. Computers and Industrial Engineering，2018，117： 319-335.

［5］Cheng Ming，Sarin S C. Lot streaming in a two-stage assembly system［J］. Annual Reviews in Control，2020，50（8）：303-316.

［6］Li Lele.Research on discrete intelligent workshop lot-streaming sche-duling with variable sublots under engineer to order ［J］. Computers & Industrial Engineering，2022，165（8）：107928.

［7］Bozek A，Werner F. Flexible Job-Shop scheduling with lot streaming and sublot size optimisation［J］.Taylor & Francis，2018，56（19）： 6391-6411.

［8］Wang Wenyan，Xu Zhenhao，Gu Xingsheng. A two-stage discrete water wave optimization algorithm for the flowshop lot-streaming scheduling problem with intermingling and variable lot sizes［J］. Knowledge-Based Systems，2022，238：107874.

［9］Da Silva I B，Godinho F M.Single-minute exchange of die （SMED）： a state-of-the-art literature review［J］.International Journal of Advanced Manufacturing Technology，2019，102（9-12）： 4289-4307.

［10］Basri A Q，Mohamed N，Nelfiyanti，et al. SMED simulation in optimising the operating output of tandem press line in the automotive industry using WITNESS software［J］. International Journal of Automotive And Mechanical Engineering，2021，18（3）： 8895-8906.

［11］Ribeiro M A S，Santos A C O，De Amorim G D，et al. Analysis of the implementation of the single minute exchange of die methodology in an agroindustry through action research ［J］. Machines，2022，10（5）：287.

［12］Ondra P. The impact of single minute exchange of die and total productive maintenance on overall equipment effectiveness ［J］. Journal of Competiveness，2022，14（3）： 113-132.

［13］Emekdar E，Acikgoz-Tufan H，Sahin U K，et al. Process improvement and efficiency analysis using the single-minute exchange of dies method applied to the set-up and operation of screen-printing machines［J］. Coloration Technology，2023，139（2）： 209-218.

［14］李瑞，徐华，杨金冯，等. 改进近邻人工蜂群算法求解柔性作业车间调度问题［J］. 计算机应用研究，2024，41（2）：438-443. （Li Rui，Xu Hua，Yang Jinfeng，et al. Improved algorithm of near-neighbor artificial bee colony for flexible Job-Shop scheduling ［J］. Application Research of Computers，2024，41（2）：438-443.）

［15］Praditwong K，Yao Xin. A new multi-objective evolutionary optimisation algorithm： the two-archive algorithm［C］//Proc of International Conference on Computational Intelligence & Security. Piscataway，NJ：IEEE Press，2006.

［16］Li Ke，Chen Renzhi，Fu Guangtao，et al. Two-archive evolutionary algorithm for constrained multi-objective optimization［EB/OL］. （2018）. https：//arxiv.org/abs/1711.07907.

［17］Gu Qinghua，Wang Danna，Jiang Song，et al. An improved assisted evo-lutionary algorithm for data-driven mixed integer optimization based on two_arch［J］. Computers & Industrial Engineering，2021，159：107463.

［18］Srinivasa R M，Mallipeddi R，Das K N. A twin-archive guided decomposition based multi/many-objective evolutionary algorithm［J］.Swarm and Evolutionary Computation，2022，71：101082.

［19］Li Wei，Gong Wenyin，Ming Fei，et al. Constrained multi-objective evo-lutionary algorithm with an improved two-archive strategy［J］. Knowledge-Based Systems，2022，246：108732.

［20］Qin Cifeng，Ming Fei，Gong Wenyin. Constrained multi-objective optimization via two archives assisted push-pull evolutionary algorithms ［J］. Swarm and Evolutionary Computation，2022，75：101178.

［21］Braglia M，Di Paco F，Marrazzini L. A new Lean tool for efficiency evaluation in SMED projects［J］. International Journal of Advanced Manufacturing Technology，2023，127（1-2）： 431-446.

［22］Zhang Huiyu，Xi Shaohui，Chen Qingxin，et al. Performance analysis of a flexible flow shop with random and state-dependent batch transport［J］. International Journal of Production Research，2020，59（4）： 982-1002.

［23］刘丽娜，南新元，石跃飞. 改进麻雀搜索算法求解作业车间调度问题 ［J］. 计算机应用研究，2021，38（12）： 3634-3639. （Liu Lina，Nan Xinyuan，Shi Yuefei. Improved sparrow search algorithm for solving Job-Shop scheduling problem ［J］. Application Research of Computers，2021，38（12）： 3634-3639. ）

［24］Zhang Bian，Pan Quanke，Meng Leilei，et al. An automatic multi-objective evolutionary algorithm for the hybrid flowshop scheduling problem with consistent sublots［J］.Knowledge-Based Systems，2022，238：107819.

［25］Caldeira R H，Gnanavelbabu A. Solving the flexible Job-Shop scheduling problem using an improved Jaya algorithm［J］. Computers & Industrial Engineering，2023，137：106064.

［26］张国辉，闫少峰，陆熙熙，等. 改进混合多目标蚁群算法求解带运输时间和调整时间的柔性作业车间调度问题 ［J］. 计算机应用研究，2023，40（5）：3690-3695. （Zhang Guohui，Yan Shaofeng，Lu Xixi，et al. Improved hybrid multi-objective ant colony optimization for flexible Job-Shop scheduling problem with transportation time and setup time ［J］. Application Research of Computers，2023，40（5）： 3690-3695.）