基于图示法的线性代数教学研究与实践

摘要：“线性代数”是一门面向低年级非数学专业大学生的核心基础课，在现代科学技术的各个领域都有着十分广泛的应用，对学生后续专业课程的学习起到重要作用。然而抽象的概念符号以及繁多的公式性质使得学生难以抓住知识的本质，疲于死记硬背，导致学习兴趣和热情降低，为学生学好这门课带来了不小的阻碍。本文围绕线性空间和线性变换这两个线性代数知识体系中的重要概念，研究利用图示教学法直观形象地解释符号背后所蕴含的知识逻辑。通过图示展示概念之间的所属关系，刻画线性空间及其子空间的结构和相互关系，帮助学生更容易地理解抽象的概念，更深入地掌握知识要点，培养学生的形象思维能力，进而激发学习兴趣，提高学习效率，达到提升课程的教学质量和效果的目标。

关键词：线性代数；图示教学法；形象化思维

中图分类号：G642文献标识码：A

“线性代数”是高等院校开设的一门面向非数学类专业的核心基础课，在现代科学技术的各个领域有着十分广泛的应用，瑞典科学家L.戈丁曾说：“如果不熟悉线性代数的概念，就去学习自然科学，现在看来就和文盲差不多，甚至可能学习社会科学也是如此。”［1］因此，让刚进入大学校园的学生能够“学好线性代数”是高等教育阶段的一项重要任务。然而，由于线性代数概念本身具有较强的抽象性，相比于微积分等数学学科，更加强调概念和性质的解释和关联，学生理解起来并不容易，从而导致学习兴趣和热情降低［2，3］。自20世纪80年代以来，图示教学法开始兴起，通过文字、符号、数字等形式构成图示结构，展示知识框架之间的逻辑关系，因其直观系统化的特点，能够大大减少需要传递的信息量，提高教学效果和效率，所以被广泛应用于数学、历史、地理等各个学科［4］。

本文围绕线性空间和线性变换这两个在线性代数知识体系中十分重要的概念［56］，探讨如何利用图示教学法，帮助学生更好地理解知识要点，激发学生学习兴趣，达到提升课程的教学质量和效果的教学目标。

1概念图示

要准确理解线性代数的概念体系，最重要的一点是厘清概念之间的所属（包含）关系，下面讨论线性空间和线性变换相关概念的图示设计方法。

1.1线性空间及其基

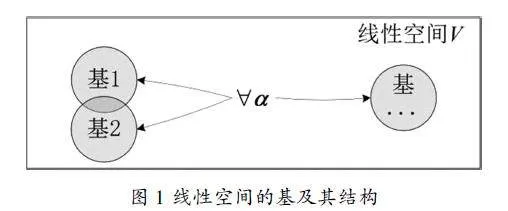
线性空间本质上是对线性运算封闭的对象的集合，而线性空间的基是其中具有特殊性质的向量组，即基向量之间线性无关，个数固定（为线性空间的维数），线性空间中的任一向量α都可以由基线性表示，并且基不唯一。因此，采用集合论中的文氏图表示方法，以矩形框（的内部区域）表示线性空间V（如图1所示），以大小相同的实心圈表示基，不同基之间可能存在公共向量也可能不相交，用箭头表示前者可由后者线性表示，得到线性空间结构的图示。

1.2线性空间的子空间

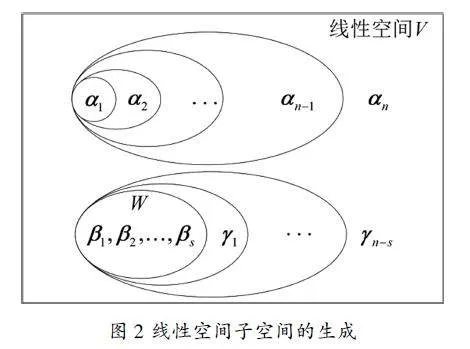
线性空间V的子空间是V中对线性运算封闭的子集。每个子空间都可以看作是由其基张成的（即由基的所有线性组合构成的）；任一向量组都可以张成一个子空间，若这个向量组线性无关，则它就构成所张成子空间的一组基。因此，同样采用文氏图的表达方法，以矩形框（的内部区域）表示n维线性空间V，设V的一组基为α1，α2，…，αn，以空心圈表示由向量组张成的子空间，则由基向量张成的子空间的结构如图2所示。进一步假设一个s维子空间W的一组基为β1，β2，…，βs，显然sn，则向这组基依次添加向量γ1，…，γn-s便可扩充为V的一组基，其中对任意γi（1in-s）都有β1，β2，…，βs，γ1，…，γi线性无关，即γi不属于β1，β2，…，βs，γ1，…，γi-1所张成的子空间，这一过程如图2所示。

1.3线性方程组解的结构

以m×n矩阵A为系数矩阵的齐次线性方程组Ax=0的解集构成n维向量空间的子空间，故可称为解空间，其一组基称为该齐次线性方程组的基础解系，不妨设为ξ1，ξ2，…，ξt；非齐次线性方程组Ax=b的解集由于不含零向量，因此并不构成向量空间，但其通解可表示为x=η+k1ξ1+k2ξ2+…+ktξt，其中η为Ax=b的一个特解，k1，…，kt取任意数，即Ax=b的所有解就是将Ax=0的每个解与η求和得到，因此两个解集的大小（当解集为无限集时即为势）相同，在几何上Ax=b的解集即是将Ax=0的解空间平移η。因此，以两个大小相同的空心圈分别表示Ax=0的解空间和Ax=b的解集，箭头表示解向量之间的对应关系（如图3所示）。

1.4欧氏空间的基、线性变换及其矩阵

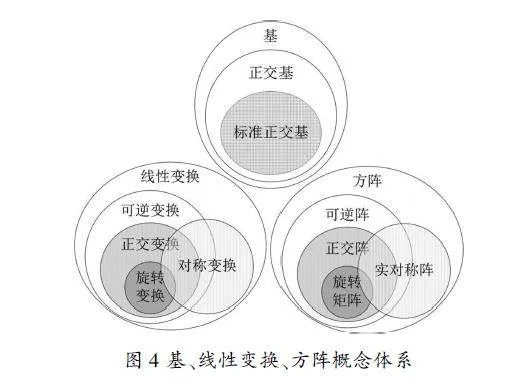
由于欧氏空间是在线性空间上引入了内积运算，因此若在基向量之间线性无关的基础上进一步要求基向量之间相互正交，则可得到正交基，更进一步要求每个基向量均为单位向量便可得到标准正交基。线性变换在一一映射的条件下即为可逆变换，若进一步要求保持向量长度不变则为正交变换，更进一步要求对空间中所有向量绕某个向量旋转某个角度即为旋转变换，而对称变换则以上情况都有可能。由于在给定一组基下，任一线性变换都与一方阵相互确定，因此方阵也相应地分为可逆阵、正交阵、旋转矩阵和实对称阵。但是需要强调的是，在任何一组基下，可逆变换与可逆阵可以相互确定，但只有在标准正交基下，正交变换才与正交阵相互确定，旋转变换才与旋转矩阵相互确定，对称变换才与实对称阵相互确定。因此，分别以大小包含的空心圈表示概念之间的所属关系，得到相关的概念体系如图4所示。

2性质图示

2.1线性空间的维数公式

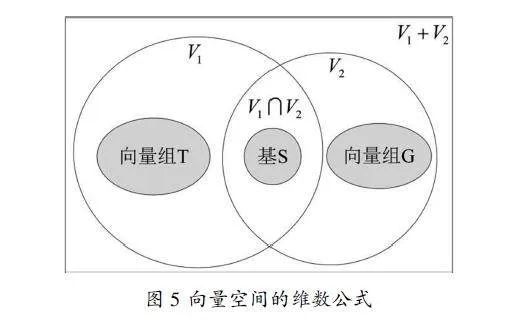
设V1，V2是线性空间中的两个子空间，则有dimV1+dimV2=dim（V1+V2）+dim（V1∩V2）.此维数公式本质上刻画了子空间V1的基、V2的基、V1∩V2的基与V1+V2的基之间的构成关系。以两个空心圈分别表示子空间V1和V2（如图5所示），这两个圈重叠的区域即表示V1∩V2，以含有这两个实心圈的矩形框（的内部区域）表示V1+V2，以一个实心圈表示V1∩V2的一组基S。由于V1∩V2为V1的子空间，所以由S可以扩充为V1的一组基，不妨设添加的向量组为T，以一个实心圈表示，显然TV1并且T中任一向量都不属于V1∩V2；同理，由S可以扩充为V2的一组基，不妨设添加的向量组为G，以一个实心圈表示，显然GV2并且G中任一向量都不属于V1∩V2，则这三个实心圈的并S∪T∪G即构成V1+V2的一组基。

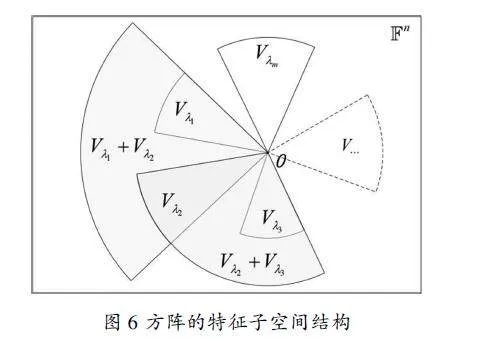
特别地，若V1∩V2=0，则S为空集，T即为V1的一组基，G即为V2的一组基，这时V1与V2之和为直和。例如，设n阶方阵有m个不同的特征值λ1，…，λm，每个特征值λi都确定一个特征子空间Vλi，由于属于不同特征值的特征向量线性无关，所以特征子空间之和也为直和，故Vλ1∩Vλ2∩…∩Vλm=0。以矩形框（的内部区域）表示特征向量所属的向量空间Fn（如图6所示），以只有一个公共顶点（零向量）的空扇面表示特征子空间Vλ1，Vλ2，…，Vλm以及Vλ1+Vλ2，Vλ2+Vλ3等和空间。由于特征子空间之间为直和，所以有（Vλ1+Vλ2）∩（Vλ2+Vλ3）=Vλ2。

2.2线性变换的维数公式

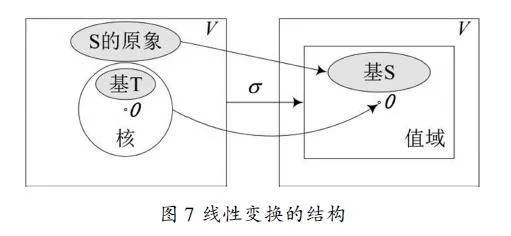
设σ为n维线性空间V上的线性变换，则有dimσ-1（0）+dimσ（V）=n.其中σ-1（0）为线性变换的核空间，σ（V）为线性变换的值域。此维数公式本质上刻画了核空间的基与值域的基之间的关系。以两个大小相同的矩形框（的内部区域）分别表示线性空间V（如图7所示），从左至右的箭头表示在线性变换σ作用下的映射关系。在左侧矩形框中以空心圈表示核空间，其一组基T以实心圈表示，以一点表示零向量；在右侧矩形框中以小矩形框表示值域，其一组基S以实心圈表示，以一点表示零向量。从核至零向量加以箭头表示σ将核中所有向量都映射为零向量。在左侧矩形框中以与基S同样大小的实心圈表示基S的原象，表示这两组向量个数相同，并以箭头连接表示σ将基S的原象中的每个向量都映射为基S中的对应向量，则值域的基S的原象与核的基T之并即构成V的一组基。由此可知，核越“小”则值域越“大”，但两者的维数之和始终不变。特别地，若核空间缩小到只含有零向量，则基T为空集，值域即为V，这时的线性变换为一一映射，故为可逆的线性变换。

3教学效果

文中所述图示，笔者已在北京航空航天大学“工科高等代数”教学中进行了实践，从2023年秋季学期笔者的教学班的问卷调查结果来看，同学们对图示教学法持积极肯定的态度，能够促进对知识的学习和理解。

结语

“线性代数”知识的抽象性是学生学习的难点，为了帮助同学更形象地理解知识要点，本文提出利用图示教学法，展示了如何将线性空间和线性变换相关的概念定义和性质从文字表述转化为图示形式，直观系统地呈现知识逻辑关系，并通过课堂实践表明图示教学法有利于培养学生的形象思维能力，激发学生的学习兴趣，提高学习效率，从而达到提升课程的教学质量和效果的目标。

参考文献：

［1］L.戈丁.数学概观［M］.胡作玄，译.北京：科学出版社，2001.

［2］李良，黄廷祝，程光辉.唤起好奇，激发志趣——在线性代数课程中融入计算思维［J］.大学数学，2022，38（4）：4043.

［3］车国凤，张丽丽.“线性代数”教学改革的思考与实践［J］.教育教学论坛，2022（28）：98101.

［4］李梦瑶.图示教学法在初中历史教学中的运用研究［D］.上海：上海师范大学，2021.

［5］李尚志.线性代数［M］.北京：高等教育出版社，2011.

［6］高宗升，周梦，李红裔.线性代数（第3版）［M］.北京：北京航空航天大学出版社，2016.

基金项目：2023年北京航空航天大学一流本科课程立项项目“工科高等代数”

作者简介：陈肖宇（1982—），男，汉族，辽宁沈阳人，博士，讲师，硕士生导师，研究方向为数学知识管理和教育数学。