深度学习导向下的初中数学大单元教学

单元整体教学是初中数学高效教学活动中重要的模式之一，相比较以往单一课时教学活动而言，单元整体教学立足全局视角，解读单元整体内容，分析学生学情，设计单元整体教学目标，制定单元教学流程，分析单元整体教学方法，设计单元整体活动等，从全局角度思考如何科学设定单元整体教学模式，多措并举共同促进初中数学大单元教学质量的提升。

【教材分析】

“勾股定理”是数与形的第一定理，古今中外无数学者对其进行了研究与证明。它刻画了直角三角形的三边关系，由“形”定“数”，体现了“数”与“形”的完美结合。勾股定理蕴含着丰富的历史文化内涵，推进了数的发展，不仅在数学领域有着重要地位，还在其他学科领域中被广泛应用。人教版“勾股定理”包含勾股定理及其逆定理等相关内容，是在学生学习了三角形、二次根式等内容之后展开的学习，是对三角形性质的深入学习，其中包含对勾股定理的探索、发现以及证明的过程，蕴含了从特殊到一般的数学思想，逆定理的证明则体现了数学思维的严谨性。勾股定理及其逆定理的学习加深了学生对直角三角形的认识，为后续矩形、二次函数综合运用等内容的学习奠定了基础。

【学情分析】

“勾股定理”是初中阶段的重难点内容，学生在勾股定理之前学习了三角形、二次根式的相关知识，从几何角度对三角形的相关知识进行了分析，从代数角度了解了二次根式的相关内容，为学生学习勾股定理奠定了良好的基础。八年级阶段的学生，从学习兴趣、学习心理等诸多方面分析，具有好奇、好强、思维活跃等特征。因此在“勾股定理”的学习与实践过程中，教师可以充分尊重学生主体，创设符合学生学习的多样化数学学习与活动平台，通过整个单元的学习，学生深入理解勾股定理相关知识。

【教学目标】

1.经历勾股定理的探索过程，感受勾股定理反映的直角三角形三边之间的数量关系，从而在探究过程中进一步发展学生的空间观念。

2.体验勾股定理的验证过程，使学生经历猜想—推理—验证的学习过程，体会数形结合、从特殊到一般的数学思想。

3.经历多角度思考问题、解决问题的过程，体验解决问题的多样化思路，拓展学生思考问题的思维方式。

4.掌握直角三角形的性质和判定，对勾股数的概念有深刻理解，能够清晰认知勾股定理和逆定理之间的关系，并能用相关知识解决实际问题。

（设计意图：单元整体教学目标的设计是以核心素养为依据，综合分析单元整体内容，随后制定系统的目标。深度学习视角下的单元整体教学以学生需求为本，使得课堂教学目标更加明确。不仅如此，在目标设定过程中，教师也明确了本单元学习的重难点内容，使学生能够进一步明确单元整体学习目标以及要达到的学习水平。）

【教学建议】

1.渗透数学文化，让学生在学习过程中获取更多的与勾股定理相关的知识，以增加学生与勾股定理相关的知识背景，为探究学习奠定基础。

2.以思维培养为基础，鼓励学生在体验、探索、应用过程中深入体会勾股定理的相关内容，使学生深入体会从特殊到一般的数学思想。

3.将学生分为学习小组，结合具体案例将抽象的概念具体化，帮助学生加深对知识的理解深度。

4.加强数学思想方法的渗透。通过勾股定理在几何问题中的应用，渗透数形结合思想、方程与函数思想、数学建模思想。

【单元整体教学流程】

【教学过程】

（一）探索勾股定理

1.整体导入环节

首先，从三角形的边角关系入手，引出学习勾股定理的必然性。（三角形两边之和大于第三边，两边之差小于第三边……）教师还可以提出操作任务：分别以3厘米、4厘米为直角边做一个直角三角形，量一量斜边的长度，并猜想这个直角三角形三边有怎样的数量关系。

其次，通过上述操作活动，教师鼓励学生以小组为单位进行设计与测量，再通过类似问题的探讨，如将直角三角形两个直角边的长改为6厘米和8厘米，那么斜边的长度是多少呢？这个直角三角形三边的关系与上一个直角三角形的三边关系相同吗？通过衔接活动引导学生猜想学习结论，合理归纳直角三角形三边数量关系，为后续探究奠定基础。

2.小组合作，探究学习

首先，教师设计探究任务，鼓励学生通过合作学习的方式对教师出示的问题进行合作讨论，给出教材第23页“探究”板块图形，提出问题。如，方格图中含有几个正方形，那么此正方形的面积为几个单位面积等，通过提出问题的方式，引导学生认真观察图片内容，并填写表格，使学生在观察、分析、数数的过程中探究数与形之间的相互转化，体会数形结合的奥秘。

其次，在第一环节图片观察与讨论的基础上，初步提炼勾股定理的大致内容，随后让学生说一说自己在第一环节中的收获，并用数学语言进行总结，如SA+SB=SC，初步归纳出勾股定理：两直角边的平方和等于斜边的平方（等腰直角三角形、一般直角三角形）。通过这一环节的设计，学生探究“从特殊到一般”的数学思想方法。

最后，教师鼓励学生用数学语言对勾股定理进行转化、表达，使其通过表达方式的转变，体会数学知识的奥秘。在此环节中，教师承接上述环节中总结的规律，让学生用符号语言正确表达勾股定理的相关表达以及形式变换，感悟“形变质通”的数学思想方法。如文字语言：直角三角形的两直角边的平方和等于斜边的平方。符号语言：∠C=90°。（已知）那么a2+b2=c2（c2-a2=b2等）。

3.验证定理，提升能力

首先，教师出示“赵爽弦图”，并借助多媒体引入数学文化，引导学生说一说自己对于“赵爽弦图”的理解，以及其中蕴含哪些知识。

其次，教师鼓励学生借助“赵爽弦图”验证勾股定理，将学生分成学习小组，然后根据三个正方形边长之间的数量关系，最终得出勾股定理。在讨论过程中，教师引导学生用“内嵌法”“外镶法”两种方法借助“赵爽弦图”证明勾股定理，深入理解“形变质通”的思想方法。

最后，教师出示加菲尔德证明勾股定理的相关图形，引导学生从另外的角度进行验证，“拼梯形图”的方式感受“总统证明法”。这一过程可以充分利用电子白板，通过线上、线下融合活动的方式，有效调动学生主动参与课堂活动的积极性。

4.简单应用，建构体系

首先，出示典型例题：“如果从电线杆离地面8 m处向地面拉一条钢索，若这条钢索在地面的固定点距离电线杆底部6 m，那么需要多长的钢索？”通过典型例题的运用，引导学生深入理解知识内涵，迁移应用数学知识解决问题，感受勾股定理的内涵。

其次，以小组为单位，分别对整堂课的知识进行梳理分析，用自己的方式呈现知识之间的联系，同时交流自己的感受，以及还有哪些问题想要深入了解。

（设计意图：单元整体视角下，探索勾股定理1课时内容设计，按照“课堂导入—深入理解—迁移应用”这一思路，打破了传统勾股定理数格子总结勾股定理的传统方式，引导学生在实际操作、数据猜想中发现勾股定理；将正方形、梯形面积等内容与勾股定理联系起来，引导学生建立知识之间的必然联系，从而将定理知识内化。在深入探究环节，以教材内容为基础，但是并没有被教材内容束缚，而是将内容适当整合，通过问题引导，使学生经历观察、操作、发现、猜想、验证的过程，实现了单元整体视角下教与学的创新。）

（二）一定是直角三角形吗

1.温故知新

通过问题引导的方式，回顾现阶段学生掌握的知识：

问题1：直角三角形有哪些性质？

问题2：如何判断三角形是直角三角形？

在上述两个问题的基础上，教师引出古埃及人得到直角的方法：“用13个等距的结，把一根绳子分成等长的12段，然后以3个结、4个结、5个结的长度为边长，用木桩钉成一个三角形，其中一个角便是直角。”教师用视频动画演示整个过程，随后请学生观察这个三角形三边的关系。

2.画一画

教师给出几组不同数字，学生以小组为单位，结合数据进行画图分析，看看是不是所给出的几组数字都能构成直角三角形。

①5，12，13；②6，8，10；③7，24，25；④2.5，6，6.5。

问题1：这几组数字都满足勾股数吗？

问题2：根据以上数字画出的三角形都是直角三角形吗？

通过观察、绘画的过程，检验学生对勾股定理知识的掌握程度。

3.说一说

问题1：你从上面几个例子发现了什么？说一说自己的观点。

此时学生可以自由发言，根据温故知新、画一画两个环节，说一说自己得出的观点：如果三角形的三边长为a、b、c，满足a2+b2=c2，那么这个三角形就是直角三角形。

问题2：你知道如何判定一个三角形是不是直角三角形吗？

通过问题2的引导，联系问题1，学生可以清晰地了解勾股定理以及逆定理之间的互逆关系，进一步加深对勾股定理的认知。

4.做一做

教师通过典型例题，引导学生将课堂所学知识应用于例题活动中，从而更进一步深化学生对勾股定理逆定理的理解深度。

例题1：判断由a、b、c组成的三角形是不是直角三角形。

（1）a=15 cm，b=8 cm，c=17 cm；（2）a=13 cm，b=15 cm，c=14 cm。

例题2：在三角形ABC中，a=15 cm，b=17 cm，c=8 cm，求这个三角形的面积。

教师设计例题，引导学生将课堂所学内容应用于例题解答过程中，在例题设计中还可以延伸到生活场景中，检验学生能否将知识融会贯通。

（设计意图：本堂课内容的设计同样使学生经历了探索、猜想、归纳、验证、应用、拓展的过程，将直角三角形的判定等内容融会贯通，并应用于实践活动中，达到提高学生应用勾股定理逆定理解决问题能力的目的。）

（三）勾股定理的应用

1.情境创设：怎么走最近

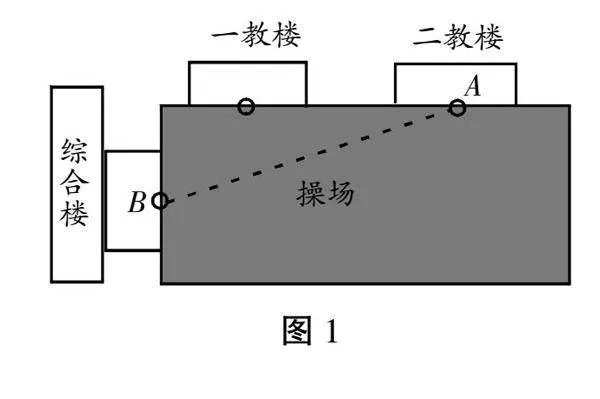
如图1，从教学综合楼的B点走到二教学楼的A点，你知道怎么走最近吗？（预设：两点之间线段最短。）

（设计意图：通过创设生活情境，学生初步认识到两点之间线段最短，为后续探究合作做好充分准备。）

2.小组合作，深度探究

情境创设：小蚂蚁从一个高是12 cm，底面上圆的周长等于18 cm的圆柱上运动，如果蚂蚁在圆柱下底面的点A处，但是它想吃到上底面上与点A相对的点B处的食物，沿圆柱侧面爬行到B点，求其爬行的最短路程是多少？

关于最短距离的问题是勾股定理延伸问题中的重难点问题，也是易错点，针对这一情境设计，教师可以将学生分为几个探究小组，然后让学生先根据自己的理解进行探究，在探究过程中，可根据学生的不同学习能力给出适当的提示。

提示1：观察手里的圆柱体（每个小组一个），你能画出几条路线呢？你觉得哪条路线最短呢？

提示2：我们曾经学习过圆柱体的展开图，那么在展开图上你能找到B点的对应位置吗？请尝试画出圆柱体的展开图，标出B点位置。

提示3：在展开图中从A点到B点的最短距离如何确定？

提示4：在圆柱体中，蚂蚁从A到B的最短路线，你觉得是哪一条呢？它沿侧面爬行了多少距离？

（设计意图：最短距离问题是勾股定理中比较典型的变式问题，通过最短距离问题的设计，一方面能够检验学生对本单元知识的学习深度，另一方面也能够将本单元所学知识融会贯通，并运用于实际问题的解决过程中。在这一过程中，学生再次经历猜想、验证、实践、反思的过程，对学生而言也是知识理解、内化的过程。）

3.迁移运用，全面提升

拓展问题1：长方体的底面边长分别为1 cm和3 cm，高为6 cm，如果一只蚂蚁从点A开始经过4个侧面爬行一圈到达点B，那么蚂蚁爬行的最短路径长为多少？

拓展问题2：一个三级台阶，每级台阶长、宽、高分别为2 dm、3 dm、2 dm，一只蚂蚁想从A点爬到其对应B点，你能帮蚂蚁设计一条最短的路线吗？求出最短路线的长。

这一环节问题设计中，教师可以采用分层设计的方式。能力较强的学习小组，学生可以自主作图，如果小组学生能力相对较差，那么需要教师给出立体图和平面图，并标注相应的数据内容，学生根据教师标注、提示，尝试解决问题。

（设计意图：通过设计分层活动，不仅实现了因材施教，还将本单元知识与相关知识点系统串联起来，使学生在解决问题的过程中建构知识体系，有效提升学生学习质量。）

【教学反思】

深度学习视角下单元整体教学设计是将单元内容看作一个整体，从整体角度对本单元知识进行综合整理与分析，制定单元整体教学目标，根据学情确定单元整体教学流程，设计驱动任务引导学生自主、合作、探究完成单元学习目标；在此基础上，教师设计了系统多样的拓展活动，将课堂知识应用于多层次问题解决过程中，使学生经历知识的内化、迁移、应用过程，最终达到提升学生学习质量的目的。

在后续单元整体教学活动中，教师还可以添加单元评价以及单元作业设计与实施环节，将评价活动与课堂教学活动衔接起来，使学生更加了解自己的学习目标，明确课堂活动的方向。教师通过单元作业的设计，检验学生对整个单元知识的学习深度、牢固程度，一则查漏补缺，二则有效拓展学生学习思路，为后续活动组织、设计以及课后延伸实践活动提供明确的方向。

（作者单位：莆田哲理中学）

编辑：温雪莲