初中数学几何章节开篇教学构思与实践

一、教学内容

本节课内容是人教版八年级下册第十七章第一节“勾股定理”，涵盖了勾股定理的引入、猜想、验证、证明和应用等方面，内容丰富，层次分明。同时，本课通过融入数学史知识和数学文化元素，如毕达哥拉斯的地砖故事和赵爽弦图，增强了课堂的趣味性和文化性，激发了学生的学习兴趣。

二、教学目标

1.通过观察、猜想、验证和证明的过程，培养学生的探究能力和数学思维能力。

2.引导学生学会从具体事物中抽象出数学规律，并运用数学知识解决实际问题。

3.通过介绍勾股定理的历史渊源和数学文化知识，培养学生的数学文化素养和民族自豪感。

三、教学重难点

教学重点：掌握勾股定理的内容，理解其证明过程，并能够运用勾股定理解决简单的实际问题。

教学难点：勾股定理的探究和证明过程，特别是通过面积法证明勾股定理的思路和方法。

四、教学过程

（一）引入新课：勾股定理的初步认识

师：同学们，我们已经学习了直角三角形的许多性质，从角的角度看，直角三角形的两个锐角互余；从边的角度看，任意两边之和大于第三边，两边之差小于第三边。今天，我们将继续探索直角三角形的另一个重要性质——勾股定理。

在预习和查阅资料后，你们对勾股定理有了哪些了解？比如，2002年北京国际数学家大会的会徽与勾股定理有什么联系？

（学生分享查阅到的资料，包括国际数学家大会的会徽、赵爽弦图、毕达哥拉斯的地砖故事等）

师：很好，这些资料不仅会让我们进一步了解勾股定理的背景和文化内涵，还向我们展示了勾股定理的历史渊源。

（设计意图：通过引导学生分享查阅到的资料，学生对勾股定理有一个初步的认识，并感受数学定理的文化内涵和历史背景。）

（二）探索勾股定理：猜想、验证与证明

师：同学们，今天我们将一起探索数学中的一个重要定理——勾股定理。这个定理描述了直角三角形三边之间的特殊关系。在数学史上，有一个有趣的传说与这个定理的发现有关。古希腊数学家毕达哥拉斯在一次聚会上，偶然间通过观察地砖的图案，发现了直角三角形三边之间的这种特殊关系。我们也来试试看，能否通过观察地砖图案，找到这种关系呢？

（教师展示地砖图案，引导学生观察）

（设计意图：通过讲述毕达哥拉斯观察地砖图案发现勾股定理的故事，激发学生探索数学定理的兴趣。）

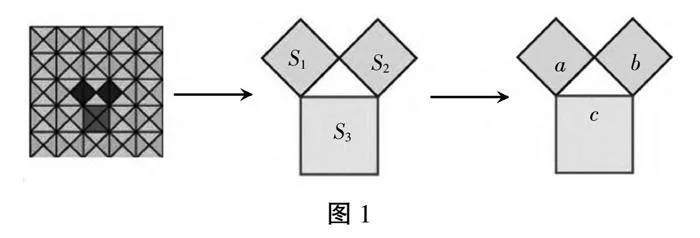
师：大家看看这些地砖，把它们抽象成如图1所示的几何图形，图中三个正方形的面积有什么关系？你能发现等腰直角三角形三边之间有什么特殊关系吗？

（学生通过观察提出猜想）

生：老师，我发现这些等腰直角三角形的两条直角边的平方和似乎等于斜边的平方。

师：你能具体说说你是怎么发现的吗？

生1：我观察了地砖的排列方式，发现每个等腰直角三角形的两条直角边可以看作是两个正方形的边长，而斜边则是另一个正方形的边长。通过计算这些正方形的面积，我发现它们之间确实存在这样的关系。

（设计意图：通过观察地砖图案中等腰直角三角形的边长关系，引导学生提出猜想。这一过程旨在培养学生的观察力和归纳能力，让他们学会从具体事物中抽象出数学规律。）

师：很好！你的观察很仔细，提出的猜想也很有价值。那么，这种关系是否也适用于其他的直角三角形呢？我们需要进一步验证。

（教师引导学生使用不同的直角三角形进行验证，并记录结果）

师：现在，请大家在网格纸上画出几个直角三角形，并测量它们的三条边。然后，计算两直角边的平方和与斜边的平方，看看它们之间是否存在刚才猜想的关系。

（学生操作后汇报结果）

生：老师，我计算了几个直角三角形，发现它们的两直角边的平方和确实都等于斜边的平方。虽然有些误差，但基本上都符合这个关系。

师：很好！大家的验证结果都表明，这个猜想在多个直角三角形中都成立。那么，我们能否证明这个猜想呢？也就是说，对于任意的直角三角形，它的两直角边的平方和是否都等于斜边的平方？

（教师引导学生思考证明方法）

师：我们可以尝试用面积法来证明这个猜想。请大家拿出上课之前发给每个小组的4个直角三角形教具，开动脑筋思考一下，这4个全等的直角三角形应如何排列、拼接、组合，可以得到一个正方形？当大家得到相应的正方形以后，再通过计算面积，你会有什么惊奇的发现？那么，请大家以小组为单位，尝试用面积法证明勾股定理。

（学生分组讨论、操作后汇报结果）

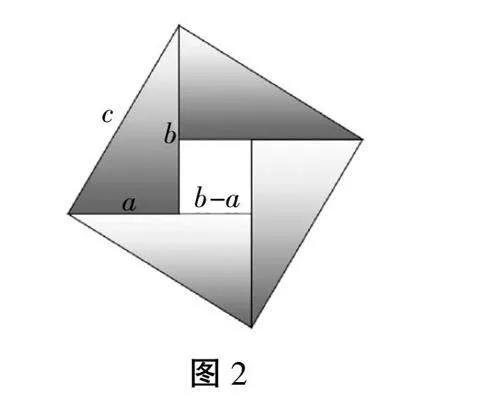
生：老师，我们小组用面积法证明了勾股定理。我们小组用4个全等的直角三角形按如图2所示拼接成一个大正方形，设直角三角形的两条直角边长分别为a，b，斜边为c，则图中大正方形的边长为c，中间的小正方形的边长为b-a，然后分别计算大正方形的面积、四个直角三角形的面积、中间小正方形的面积，我们得出了勾股定理的公式：a2+b2=c2。

师：非常棒！你们的证明方法很正确，思路也很清晰。这就是勾股定理的证明过程之一。其实，勾股定理的证明方法有很多种，感兴趣的同学可以课后去查阅相关的资料，了解更多的证明方法。

（设计意图：引导学生使用不同的直角三角形进行验证，并记录结果。这一过程旨在强化学生的实践操作能力，让他们通过亲身体验来验证猜想的正确性。同时，这也体现了数学学习中从特殊到一般的探究思路。）

师：我还要告诉大家一个有趣的数学历史知识。我们刚才用面积法证明勾股定理的方法，其实早在我国古代就有人使用了，这个方法被称为“赵爽弦图”。赵爽是东汉末年的数学家，他通过这种方法巧妙地证明了勾股定理。这不仅体现了古人对数学的钻研精神和聪明才智，也让我们感受到了数学文化的魅力。

师：同学们，我们已经通过猜想、验证和证明，发现了勾股定理这一重要的数学规律。现在，让我们来看看这个定理在实际问题中的应用吧。

师：请大家看例题，图3中的直角三角形有一个未知边x，我们如何利用勾股定理求出x的长度呢？

（思考后学生板演）

生1：根据勾股定理，直角三角形的两直角边的平方和等于斜边的平方。所以，我们可以设直角三角形的两条直角边分别为a和b，斜边为c，则有a2+b2=c2。在这个问题中，已知a和b的长度，我们可以通过勾股定理求出c的长度，即x的值。

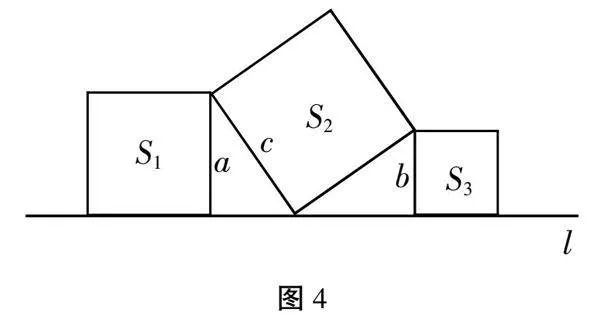
师：很好！同学们已经能够熟练运用勾股定理解决简单的实际问题了。那么，请大家再思考一下，如果将3个正方形按图4所示的方式放置在直线l上，其中正方形S1和S2的面积分别为16和25，那么正方形S3的面积是多少呢？

（学生思考、讨论）

生：根据勾股定理，我们可以将这个问题转化为求直角三角形的问题。设正方形S1的边长为a，正方形S2的边长为c，正方形S3的边长为b。通过一线三垂直模型可以证明图中的两个直角三角形全等，从而得到两个直角三角形的对应边相等。由于正方形的面积等于边长的平方，所以a2=16，c2=25，根据勾股定理，我们可以求出b2的值，即正方形S3的面积。

师：非常棒！同学们已经能够灵活运用勾股定理解决更复杂的数学问题了。通过这两个例子，我们可以看到勾股定理在实际问题中的广泛应用。那么，请大家回顾本节课的学习内容，回答问题：勾股定理的内容是什么？它有什么作用？

生1：勾股定理的内容是直角三角形的两直角边的平方和等于斜边的平方。它的作用是可以帮助我们求出直角三角形中未知边的长度或者判断一个三角形是否为直角三角形。

师：在探究勾股定理的过程中，大家经历了怎样的探究过程？

生2：我们首先通过观察地砖图案提出了猜想，然后通过验证和证明确认了猜想的正确性。在验证和证明的过程中，我们使用了不同的直角三角形进行验证，并运用了面积法进行证明。

（设计意图：通过例题和练习的讲解与讨论，引导学生将勾股定理应用于实际问题中，培养学生的应用意识和解决问题的能力。同时，通过回顾本节课的学习内容和探究过程，帮助学生巩固所学知识并加深对勾股定理的理解。在回答问题的过程中，鼓励学生从不同的角度思考并表达自己的观点和感受，促进学生的数学思维和语言表达能力的发展。）

五、教学反思

本节课通过引导学生经历观察、猜想、验证和证明的过程，让学生自主探索并理解勾股定理。从课堂效果来看，学生在教师的引导下能够积极参与探究活动，提出有价值的猜想，并通过实践操作验证猜想的正确性。在证明环节，虽然部分学生对面积法的理解不够深入，但在教师的引导和小组讨论中，学生最终能够掌握证明方法并得出正确的结论。

在教学过程中，我注重培养学生的观察力和归纳能力，引导学生从具体事物中抽象出数学规律。同时，通过融入数学史知识和数学文化元素，增强了课堂的趣味性和文化性，激发了学生的学习兴趣。在例题的讲解与讨论中，我注重引导学生将勾股定理应用于实际问题中，培养他们的应用意识和解决问题的能力。

然而，本节课也存在一些不足之处。首先，在引导学生进行猜想时，部分学生观察得不够仔细，提出的猜想不够准确。这需要教师在今后的教学中加强对学生观察能力和归纳能力的培养。其次，在证明环节，部分学生对面积法的理解不够深入，导致证明过程出现困难。这需要教师在后续的教学中加强对面积法的讲解，帮助学生更好地掌握这种方法。

综上所述，本节课在引导学生探究勾股定理方面取得了一定的成效，但也存在一些不足之处。在今后的教学中，我将继续改进教学方法和手段，加强对学生观察力、归纳能力和实践能力的培养，提高课堂教学效果。同时，我也将注重与学生的互动和交流，关注学生的需求和困惑，为他们的数学学习提供更好的支持和帮助。

（作者单位：山东省济宁市嘉祥县第四中学）

编辑：张俐丽