结构化教学视域下关于初中数学微课教学的探索与思考

“综合实践课”是围绕某个主题，让学生运用所学的综合知识解决真实的情境问题，本文以数学情境为背景，立足教学内容结构化与认知方法结构化，依托“微课”的形式实施教学流程，让学生的课前—课中—课后形成三维学习系统，在问题的探究过程中学会提出问题、分析问题、解决问题，进而培养优秀的思维品质。

一、教学目标

1.经历猜想、证明与拓广的正方形、矩形“倍增（减半）”的过程，提升发现和提出问题的能力。

2.在探究问题结论和论证结论正确性的过程中，综合运用所学知识，体会知识之间的内在联系，形成对数学的整体性认识。

3.在探究过程中，感受由特殊到一般、数形结合的思想方法，体会证明的必要性。

4.在合作交流的过程中，拓展思路，提升学生的推理能力。

二、教学重难点

1.猜想、证明与拓广的正方形、矩形“倍增（减半）”的问题。（重点、难点）

2.方程的模型建立与求解，方程、不等式及函数等知识的综合运用。（重点）

三、教学实施与分析

（一）微课课前预习

【提出问题】

教师课前布置两项学习任务，并将任务二的探索与研究成果录制成微课，结合课堂的核心问题进行展示。

◆任务一：已知，直线y=-x+k，双曲线y=4/x，

（1）若k=5，直线与双曲线的交点坐标是什么？

（2）已知，直线y=-x+k，双曲线y=4/x，若k=1，问：直线与双曲线是否有交点？请说明理由。

◆任务二：你能否制作一个新模具（正方形或矩形）：选定一个模具为参照物，使新模具的周长是原来模具周长的2倍，面积也是原b982bdac9be531f907e398e632c25d934ea7720a4b99fa90b92094c81ddca23b来模具面积的2倍吗？

已知给定的正方形模具的边长为10 cm，矩形模具的长为20 cm，宽为10 cm。

（二）微课课堂教学

【分析问题】

问题1：任意给定一个正方形，是否存在另一个周长和面积分别是已知正方形周长和面积的2倍的正方形？你是怎么做的？你有哪些解决方法？

问题2：（1）任意给定一个矩形，它的长和宽分别为2和1，是否一定存在另一个周长和面积分别是已知矩形周长和面积的2倍的矩形？（2）任意给定一个矩形，它的长和宽分别为n和1，是否存在另一个周长和面积分别是已知矩形周长和面积的2倍的矩形？（3）任意给定一个矩形，它的长和宽分别为n和m，是否存在另一个周长和面积分别是已知矩形周长和面积的2倍的矩形？

【解决问题】

基于问题1：假设原正方形的边长为a。

（1）假设=，则大正方形的边长为2a，则=≠，所以不存在这样的正方形。

（2）假设=，则大正方形的边长为a，则==≠，所以不存在这样的正方形。

【结论一】任意给定一个正方形，不存在另一个周长与面积分别是已知正方形周长和面积的2倍的正方形。

基于问题2（1）：

①问题转化为若C大矩形=12，那是否有S大矩形=4？

设大矩形的长为x，则宽为（6-x），

x（6-x）=4有解，则存在这样的矩形，若方程无实根，则不存在这样的矩形。

②也可以将问题转化为若S大矩形=4，那么是否有C大矩形=12？

设大矩形的长为x，则宽为，

（x+）×2=12有解，则存在这样的矩形，若方程无实根，则不存在这样的矩形。

③也可设大矩形的长为x，宽为y，则有：

x+y=6xy=4，则x2-6x+4=0，解得x1=3+x2=3-

所以存在长为3+，宽为3-的矩形。

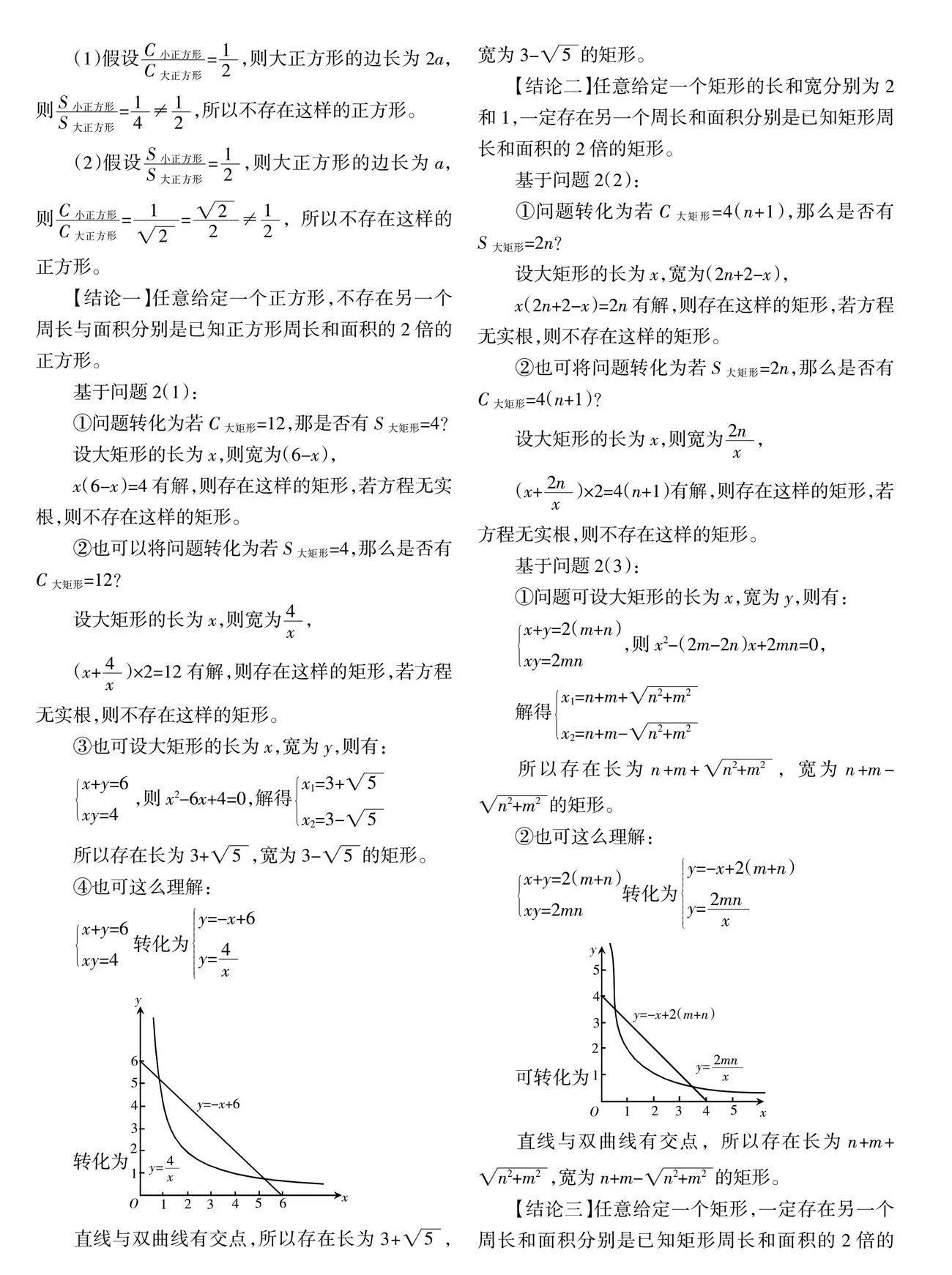
④也可这么理解：

x+y=6xy=4转化为y=-x+6y=

转化为

直线与双曲线有交点，所以存在长为3+，宽为3-的矩形。

【结论二】任意给定一个矩形的长和宽分别为2和1，一定存在另一个周长和面积分别是已知矩形周长和面积的2倍的矩形。

基于问题2（2）：

①问题转化为若C大矩形=4（n+1），那么是否有S大矩形=2n？

设大矩形的长为x，宽为（2n+2-x），

x（2n+2-x）=2n有解，则存在这样的矩形，若方程无实根，则不存在这样的矩形。

②也可将问题转化为若S大矩形=2n，那么是否有C大矩形=4（n+1）？

设大矩形的长为x，则宽为，

（x+）×2=4（n+1）有解，则存在这样的矩形，若方程无实根，则不存在这样的矩形。

基于问题2（3）：

①问题可设大矩形的长为x，宽为y，则有：

x+y=2（m+n）xy=2mn，则x2-（2m-2n）x+2mn=0，

解得x1=n+m+x2=n+m-

所以存在长为n+m+，宽为n+m-的矩形。

②也可这么理解：

x+y=2（m+n）xy=2mn转化为y=-x+2（m+n）y=

可转化为

直线与双曲线有交点，所以存在长为n+m+，宽为n+m-的矩形。

【结论三】任意给定一个矩形，一定存在另一个周长和面积分别是已知矩形周长和面积的2倍的矩形。

（三）课后学习

【迁移问题】

本部分有2个环节：（1）第1课时作业；（2）第2课时学习。

▲第1课时作业

综合实践活动：你能否制作一个新模具（正方形或矩形），选定一个模具为参照物，使得新模具的周长是原来图形周长的一半，面积也是原来图形面积的一半？请将探索的过程和成果录制成微课展示。已知给定的正方形模具的边长为10 cm，矩形模具的长为20 cm，宽为10 cm。

▲第2课时学习

问题3：任意给定一个矩形，是否一定存在另一周长和面积分别是已知矩形周长和面积的一半的矩形？

观点1（第1小组展示）：一定存在。

理由：我们已经证明了“任意给定一个矩形，是一定存在另一个周长和面积分别是已知矩形周长和面积的2倍的矩形”，也就是说任意一个矩形都有对应的加倍矩形；那反过来，原矩形自然满足新矩形的“减半”要求，也就是原矩形的周长和面积是新矩形周长和面积的一半。

观点2（第2小组展示）：一定不存在。

理由：从长和宽分别为2和1的矩形入手，设新矩形的长为x，则所求矩形的宽为y，由题意得：

2（x+y）=（2+1）×2×xy=2×1×

化简得2x2-3x+2=0。

Δ=（-3）2-4×2×2=9-16＜0，所以此方程没有实数根。即不存在这样的新矩形，使得它的周长和面积分别是已知矩形周长和面积的一半。

观点3（第3小组展示）：可能存在。

理由：设已知矩形的长和宽分别为m和n，所求矩形的长为x，则所求矩形的宽为（m+n）-x，由题意得x（m+n）-x=mn

化简得2x2-（m+n）x+mn=0

Δ=（m+n）2-4×2mn=m2+n2-6mn

①若Δ≥0，即m2+n2-6mn≥0，方程有解，即已知矩形的长为m，宽为n，满足m2+n2≥6mn时存在一个新矩形，使得它的周长和面积分别是已知矩形周长和面积的一半。

②若Δ＜0，即m2+n2-6mn＜0，方程没有实数根，即已知矩形的长为m，宽为n，满足m2+n2＜6mn时，不存在一个新矩形，使得它的周长和面积分别是已知矩形周长和面积的一半。

【总结归纳】

1.解决这类问题的一般策略是：先固定所求矩形的一个量，这样的矩形一般很多，在这些矩形中看有没有满足另一个量的矩形，若有，则这样的矩形存在；若没有，则这样的矩形不存在。验证“存在性”的问题，可以转化成如下问题来探究：

（1）方程（组）是否有解。

（2）两个函数图象有无交点。

2.本节内容用到的数学思想有：数形结合；建立方程（组）、函数的数学模型；从特殊到一般的探索策略（即猜想—验证—结论）。

四、教学思考

（一）构建双线并行的教学策略，优化思维品质

遵循认知规律，制定“真实情境—资源整合—思维建构—创新发展”和“提出问题—分析问题—解决问题—迁移问题”相融合的“双线并行”教学策略，旨在让学生用创造数学知识的方法学习数学，从解释、阐明、应用、洞察、移情、自知等方面理解学科事实，建立能体现数学学科本质、对未来学习有支撑意义的数学知识体系，学会用整体的、联系的、发展的眼光看问题，形成学科思维，发展核心素养。

（二）打破传统教学壁垒，革新育人方式

结构化教学在学生表达、操作、反思等学习活动中，关注学生的实践意识和创新意识，增强自我效能感，重构认知结构，其最终价值在于发展学生终身学习、终身成长的品质，革新了育人新方式。

（作者单位：广东省深圳市宝安第一外国语学校〈集团〉初中部）

编辑：赵文静