中垂线遗传融合算法研究

摘 要：为改善遗传算法的局部寻优性能和收敛速度，提出了一种将遗传算法和中垂线相算法结合的融合算法——中垂线遗传算法。中垂线遗传算法以遗传算法进行全局搜索，再以中垂线算法进行局部搜索。并将中垂线算法中的单一种群分化为双种群，将双种群中的优秀个体进行耦合交叉和变异，提升改进算法的全局搜索能力和跳出局部最优的能力。仿真实验讨论了算法转换系数的变化对改进算法性能的影响。通过与6个算法的对比实验，证明改进的中垂线遗传算法解决了传统遗传算法收敛速度慢和局部寻优能力弱的问题。并且与主流优化算法和其他遗传融合算法相比，改进的算法性能更加优越。最后，利用改进算法处理了三杆桁架的设计问题，结果表明了中垂线遗传算法在处理实际问题时具有可行性。

关键词：遗传算法 中垂线算法 融合算法 双种群 三杆桁架设计

中图分类号：TP3-05

Research on the Genetic Midperpendicular Fusion Algorithm

CHEN Wei HE Yujie WU Dafei

Yunnan Land and Resources Vocational College， Kunming， Yunnan Province， 652501 China

Abstract： In order to improve the local optimizaton performance and convergence speed of the genetic algorithm， this paper proposes a fusion algorithm that combines the genetic algorithm and the midperpendicular algorithm： the genetic midperpendicular algorithm. The genetic midperpendicular algorithm performs global search with the genetic algorithm and then local search with the midperpendicular algorithm， and it differentiates a single population in the midperpendicular algorithm into a double population， and cross-couples and mutates the excellent individuals in the double population， so as to improve the global search ability and the ability to jump out of the local optimum of the improved algorithm. Simulation experiments discuss the effect of the variation of the conversion coefficients of the algorithm on the performance of the improved algorithm. Through comparison experiments with six algorithms， it is proved that the improved genetic midperpendicular algorithm solves the problems of the slow convergence speed and weak local optimization ability of the traditional genetic algorithm. Compared with the mainstream optimization algorithm and other genetic fusion algorithms， the performance of the improved algorithm is more superior. Finally， the improved algorithm is used to deal with the design problem of the three-rod truss， and results show that the genetic midperpendicular algorithm is feasible in dealing with practical problems.

Key Words： Genetic algorithm; Midperpendicular algorithm; Fusion algorithm; Double population; Three-rod truss design

遗传算法（Genetic Algorithm ， GA）通过模拟自然界的基因变化和自然选择过程进行工作 [1，2]。虽然遗传算法具有良好的全局搜索能力，但局部搜索能力较差，且迭代速度较慢，因此对于遗传算法的改进一直是研究的热点。改进遗传算法的方式众多，如改进编码方式[3]、优化种群规模[4]、优化遗传操作[5]等，以其他算法与遗传算法相结合的方式效果显著[6]。因此，许多学者已对混合遗传算法进行了深入研究。如吴永忠等人[7]以自适应模拟退火遗传算法解决传统遗传算法局部搜索精度不高的问题，该方法虽提升了遗传算法的局部搜索性能，但改进算法收敛速度较慢且局部搜索性能仍较低。武晓金等人[8]将免疫算法与遗传算法结合起来，构建了免疫遗传算法，扩大了遗传算法的应用范围。徐雨等人[9]成功将免疫遗传算法应用于车间调度的求解，但该方法没有提升算法的局部搜索性能，对收敛速度的改善不大。徐金梧等人[10]提出运用小生境技术解决传统遗传算法的多种不足。

上述融合算法虽改善了遗传算法的一定性能，但改进算法的收敛速度和局部寻优性能乃至于实用性还有进一步改善的空间。中垂线算法（Midperpendicular Algorithm，MA）依托于中垂线上的任意一点到被垂直平分的线段端点的距离相等这一性质进行工作。MA局部搜索能力较强，迭代速度快，但全局搜索能力较弱。本文提出将GA与MA进行融合，以GA进行全局搜索，以MA进行局部搜索；同时将MA的种群分化为双种群，在每次迭代结束后，将双种群优秀个体进行耦合交叉和变异操作，籍此解决MA和GA存在的一些问题。

1 遗传算法与中垂线算法结合算法

1.1 遗传算法

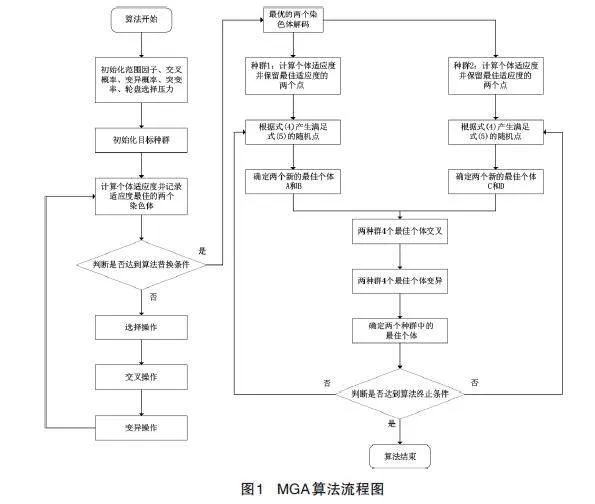
GA通过模拟生物进化中的基因选择和自然选择过程进行寻优操作，具体寻优过程为将问题抽象为染色体，其中一个染色体对应一个问题的解，利用适应度评价染色体后，适应度好的个体有更高的概率被保留，保留的染色体再进行交叉、选择、变异等方式产生下一代染色体，直至找到最优点。算法的基本步骤为：（1）初始化算法参数，生成初始群体；（2）计算初始群体中每个个体的适应度；（3）判断终止条件，若满足终止条件则进行解码操作后结束算法；（4）利用选择、交叉、变异产生新群体。

1.2 中垂线算法

中垂线算法的核心原理是以线段的中垂线上的任意一点到该线段的两个端点之间的距离相等的性质不断缩小寻优区间，直至寻到最优点。算法通过选取当前最优的两个点A和点B作为线段的端点，作出该线段的中垂线后，中垂线可将固定的取值区域分割为两部分，一部分为A点所在区域，另外一部分为B点所在区域，若最优点P居于A点所在区域，则必存在以下条件，

即P点到A点的距离小于P点到B点的距离。依照以上规律，在算法中，MA通过计算点A和点B的适应度，即可确定最优值所在区域。之后在该区域内随机取点，重复上述操作即可找到最优值。

假定粒子，并定义每次迭代选取的两个最优粒子A和B为

算法产生初始个体j的第i个元素的公式为：

其中为的最小值，为的最大值，表示0-1的随机数。算法开始迭代后，产生新个体j的第i个元素的公式为：

式（3）中：为当前迭代次数；为最大迭代次数；为范围因子。

产生的新的点须有任意两个维度的值需满足以下条件

其中

算法终止条件为

式（6）中：为当前最优粒子的适应度；为设定的精度因子。

算法的步骤为：（1）初始化参数：包括最大迭代次数，范围因子，精度因子，个体取值范围和；（2）根据公式2产生初始粒子，并评价粒子的适应度；（3）选择适应度最佳的粒子作为粒子A和B；（4）根据式（3）产生新粒子，并判定新粒子是否符合公式4的条件，若不满足，则重新产生新粒子。直至生成的粒子达到种群数。（5）判断是否满足公式6的算法终止条件，若满足，则终止算法，否则跳转至（3）。

1.3 中垂线遗传算法

1.3.1 中垂线遗传算法的搜索策略

GA的全局搜索能力良好，但算法收敛速度慢，局部搜索能力较差；MA的全局搜索能力偏弱，但算法收敛速度极快，且有较好的局部搜索能力。将GA与MA结合，组成一种组合算法—遗传中垂线算法（Genetic Midperpendicular Algorithm，GMA）。GMA前期利用GA进行全局搜索，若GA搜索到的最佳粒子的适应度满足人工设定参数或设定GA的迭代次数k达到人工设定参数γ，即

（7）

则改用采用MA进行局部搜索。

1.3.2 中垂线遗传算法的双种群耦合交叉变异策略

交替算法进行搜索的策略虽使得GMA具备GA的全局搜索性能和MA的局部搜索性能，但无法提升GMA跳出局部最优的能力，为此，引入一种双种群耦合交叉变异的策略，进一步提升算法的全局寻优能力和跳出局部最优的能力。

当MGA交替到MA进行局部搜索后，该策略将种群分化为种群1和种群2。设定GA和MA交替时，种群1的最佳两个体分别为A和B，种群2的两个最佳两个体分别为C和D。且有，。两个种群按照MA的搜索策略搜索最优值，搜索过程中两种群完全独立。

为减少MGA的时间复杂度，采用实数编码方式进行交叉和变异操作。当每次迭代结束后，两种群的两个最佳个体随机进行交叉，当任意个体进行交叉操作时，其余三个体被选为交叉对象的概率相同，交叉概率Pc控制两个体的交叉概率。当交叉结束后，每个个体会进行变异操作，变异概率Pm控制个体基因的变异概率，当第k次迭代时个体的第j个变量需进行变异时，按MA的收敛策略完成变异，即

可得到交叉变异后的个体、、和，将初始最优个体A、B、C和D与变异后的个体进行比较，若交叉变异后的个体适应度更优，则代替初始最优点。

MGA算法流程图如图1所示。

2 仿真实验与分析

2.1 准备工作

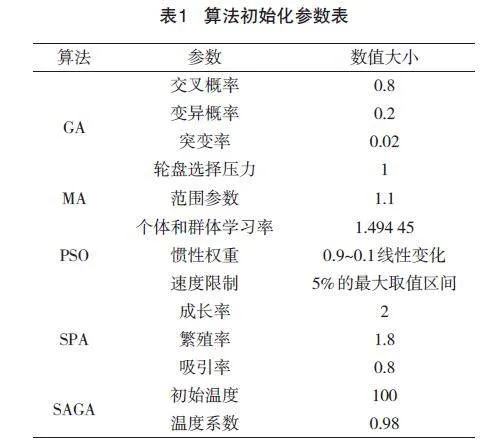
实验的6个对照算法：遗传算法、中垂线算法、粒子群优化算法（Particle Swarm Optimization， PSO）、多肉植物算法[11]（Succulent Plant Algorithm， SPA），模拟退火遗传算法（Simulated Annealing Genetic Algorithm， SAGA），遗传粒子群算法（Genetic Particle Swarm Optimization Algorithm， GPSOA），算法初始参数设定如表1所示（其中所有遗传融合算法遗传算法部分参数设置同遗传算法，融合粒子群算法参数同粒子群优化算法），本节所有实验的算法种群个数均为50，最大迭代次数为500次。

为验证新算法的性能，以MGA对8个常见的基准函数进行寻最优值。8个基准函数见表2。包括两个单模态函数（F1，F2），4个多模态函数（F2-F6），2个固定维度函数（F7，F8）[10-13]。

2.2 MGA参数分析

在MGA中，参数或γ的选取会直接影响算法的性能，为确定和γ对算法的影响，选取了三个函数F1（单模态函数）、F6（多模态函数）、F7（固定维度函数），设定不同的和γ，独立运行30次MGA并记录最终结果的均值（Mean），平方差（Std），结果如表3和表4所示。

由表3可看出，随着的变化，MGA的收敛精度和稳定性呈现不规则变化，F1和F7的数据均表明，选择合适的可提升MGA的稳定性和收敛精度。从3个目标函数的结果来看，的值不应过大。

从表4中可以看出，随着γ的变化，MGA的收敛性和稳定性呈现无规则变化。处理不同函数，MGA的最佳γ均不同，且最佳γ的取值需根据实际函数确定。

不同λ参数下，MGA收敛情况如图2所示。由图可看出，参数设定得越大，则MGA的收敛速度越快。由以上分析可得，选取λ时，首先应确保λ大于GA寻找到的最优值；若想提升MGA的全局搜索能力，λ不应设置过大；若想提升MGA的收敛速度，应设定相对较大的λ。

不同γ参数下，MGA收敛情况如图3所示。MGA的收敛速度随着γ的增加不断减慢。结合表4数据，当MGA采用γ为交换算法的条件，若想提升算法的收敛速度应选择较小的 γ。

2.3 MGA收敛精度分析

为确定MGA的收敛精度，以MGA对表1所示目标函数进行30次独立寻优。选用迭代次数进行遗传中垂线算法的转换且设γ=25。为突出MGA算法的优越性，选取6个其他算法进行相同操作，结果如表5所示。由表5可得，在F5、F6和F8的目标函数寻优中，GMA在7种算法中收敛精度的表现最好；当目标函数为其他函数时，MGA的表现一般。GMA在所有目标函数的测试中的收敛精度表现均优于GA和MA，并且同其他两种主流遗传融合算法相比，收敛精度表现最佳。

2.4 MGA稳定性分析

由表5可看出，当目标函数为F5，F6时，MGA稳定性在7种算法中表现最佳，当目标函数为其他函数时MGA的稳定性均位于中游水平。且相较于GA和MA，除目标函数为F4和F8时，MGA的稳定性均优于二者。同其他主流算法和遗传融合算法相比，同样具有极强的竞争力。

2.5 MGA收敛速度分析

7种算法在不同的目标函数中的收敛情况如图4所示，从图中可看出，在各算法处理众多函数的收敛过程中，虽MGA的收敛速度慢于MA ，但相比于GA，MGA的收敛速度大幅增加，缓解了GA收敛速度慢的问题；同其他流行的主流算法相比，MGA的收敛速度更加优越；与两种遗传融合算法相比，MGA的收敛速度同样更快。

3 三杆桁架设计问题分析

三杆桁架设计是一个工程问题，设计的目标是在考虑到应力约束和体积的情况下，评估最佳横截面积。图5显示了三杆桁架的结构。问题的数学描述如下：

由MGA独立处理该问题30次，MGA利用迭代次数转换算法，且γ=25，种群数为50，最大迭代次数为500次，结果如表6所示。从表中可以看出MGA的寻优结果均为在时取值158.58。说明MGA在处理真实工程问题具有可行性。图6为MGA处理三杆桁架算法收敛曲线。

4 结语

本文将GA与MA算法进行融合，首先以GA进行全局搜索，达到算法转换条件后，再以 MA进行局部搜索的策略融合两种算法，再以MA双种群耦合交叉变异策略增强了算法跳出局部最优的能力和算法的稳定性。仿真实验表明MGA改善了MA局部搜索能力不足，GA收敛速度慢、局部搜索能力弱的问题。同主流算法相比，MGA无论是稳定性、收敛精度和收敛速度均具备极强的竞争力。同其他两种遗传融合算法相比，MGA更加优越。最后，成功将MGA应用于三杆桁架的设计问题中，证明了MGA应用于实际问题的可行性。

参考文献

[1] 郑立平，郝忠孝.遗传算法理论综述[J].计算机工程与应用，2003（21）：50-53，96.

[2] 马永杰，云文霞.遗传算法研究进展[J].计算机应用研究，2012，29（4）：1201-1206，1210.

[3] 李韪韬，王惠南，钱志余.遗传算法的一种新颖编码研究[J].信息与控制，2006（5）：624-628，633.

[4] 史明霞.多种群协同演化遗传算法[J].商丘师范学院学报，2006（2）：72-74.

[5] 潘家文，钱谦，伏云发等.模糊自适应并行遗传算法在函数优化中的应用[J].小型微型计算机系统，2021，42（11）：2313-2322.

[6] 吴玫，陆金桂.遗传算法的研究进展综述[J].机床与液压，2008（3）：176-179，172.

[7] 吴永忠，刘华威，侯诗文等.模拟退火遗传算法在风力提水机翼型优化设计中的研究[J].太阳能学报，2021，42（6）：385-390.

[8] 武晓今，韩生廉.免疫-遗传系统的构造及在函数寻优中应用[J].辽宁工程技术大学学报（自然科学版），2001（5）：669-672.

[9] 徐雨，黄海松，胡涞.一种求解车间调度的混合免疫遗传算法[J].机械设计与制造，2020（9）：287-291.

[10] 徐金梧，刘纪文.基于小生境技术的遗传算法[J].模式识别与人工智能，1999，12（1）：104-108.

[11] ONG K，ONG P，SIA C K. A carnivorous plant algorithm for solving global optimization problems[J].Applied Soft Computing，2021，98：106833.