一种拱桥施工塔架扣索索鞍摩阻系数的计算方法

作者简介：于远志（1991—），硕士，工程师，研究方向：桥梁施工技术。

文章从数学微分原理出发，结合施工现场监测数据，推导了拱桥施工塔架扣索索鞍摩阻系数的计算式，并以平南三桥和新圩红水河特大桥为实例依托，通过测定、校验、复验及应用4个步骤证明了计算式的准确性和普适性。

平南三桥；拱桥塔架；扣索索鞍；滑轮摩阻系数

U448.22A451594

0 引言

塔架扣索索鞍常作为拱桥缆索吊装法施工中拱肋扣索的支撑过渡装置，其与塔架结构、拱上扣挂装置、扣索及张拉锚固装置等共同组成拱肋节段安装扣挂体系，见图1。扣索索鞍通常为工厂加工制作完成的钢制标准构件，施工中多采用单滑轮式扣索索鞍与滑轮组式扣索索鞍2类结构形式，见图2。索鞍的材料特性、结构形式及尺寸等因素决定了扣索索鞍与扣索接触面具有特定的摩阻系数，这是索鞍与扣索间存在一定摩阻力，导致扣索张拉后在索鞍处出现较大应力损失的根本原因。在实际施工中准确掌握扣索索鞍摩阻系数是保证在扣索两侧施加足够应力值和保证拱肋安装节段精确定位且后期不发生下沉变形的关键。

大量工程师和研究人员对这类问题研究做出了巨大努力和探索，但不少由于扣索张力值不足导致拱肋安装节段出现下沉、变形、甚至失稳等严酷事实表明我们对扣索索鞍的摩阻系数还应进一步研究和了解。领域内对其的研究大都基于数值仿真模拟或现场荷载试验得到扣索张拉端与锚固端的张力差值，以求得索鞍与扣索特定组合条件下的扣索索鞍的摩阻系数与应力损失百分比。例如秦大燕等［1］设计并进行了平南三桥塔架扣索索鞍节段1∶1现场荷载试验，得到了不同张拉荷载工况下扣索张拉端与锚固端的张力值，并通过计算发现平南三桥各扣索与索鞍之间的摩阻系数约为4%（单滑轮式扣索索鞍）与3.2%（滑轮组式扣索索鞍）；刘佳辉［2］利用仿真数值模拟，并结合现场足尺模型试验，研究了某矮塔斜拉桥弧形板索鞍的摩阻性能，发现索鞍抗滑装置和摩阻力共同承担了99%以上的索力差；王路［3］利用主缆侧向力计算方法及实用公式对温州瓯江北口大桥主索索鞍摩阻力进行了计算，同时分析了其组成机理，并通过模型试验评估主索索鞍的摩阻性能；贺拴海等［4］以山西洰河桥及厦门海沧大桥为实例依托，采用理论公式推导和有限元算法得到了悬索桥索鞍摩阻力的精确算法。

以上研究均未充分认识到塔架扣索索鞍为材料特性、结构形式和断面特性确定的标准构件，且能够多次在类似桥梁工程中周转利用的重要事实，若仅针对某单一桥梁工程开展索鞍摩阻系数试验或数值模拟研究，其研究结果对实际施工虽具有参考意义，但指导后续工程的经济性和普适性值得怀疑。本文以实际工程为例，从数学微分原理出发，并结合现场扣索索力监测数据，求得扣索索鞍摩阻系数的普适计算公式，为索鞍在周转利用工程中提供技术依据，达到避免重复试验和经济节约的目的。

1 摩阻系数计算及应用方法

1.1 确定参数

为方便计算，将扣索与扣索鞍接触面设定为连续圆弧面，计算参数包括：扣索锚固端一侧张力值T1；扣索张拉端一侧张力值T2，即扣索张拉的控制应力值，显然T1＜T2；连续圆弧面半径R；连续圆弧面弧度θ=θ2-θ1。可见计算选用参数极为简洁，且容易在施工现场获取，见图3。

1.2 公式推导

扣索与扣索鞍接触面上任取一微元A，设微元两端的张力分别为Ti和Ti+1，则微元A处受到的合摩阻力为ΔFi=Ti+1-Ti，微元A对应的圆弧弧度为Δθ，易知Ti和Ti+1形成一通过圆心正压力Ni，见图4。

可见，式（12）表明扣索索鞍摩阻系数f可以表达为扣索与扣索索鞍接触面合摩阻力FW、扣索锚固端一侧张力值T1、扣索与扣索鞍接触面圆弧度值θ三者之间的函数关系。

1.3 应用方法

公式的应用方法分为测定、校验、复验及应用4个步骤，以检验公式的准确性和普适性。

（1）测定：在施工现场选定一组扣索与扣索鞍组合，利用监测设备测定扣索张拉端一侧张力值T2和锚固端一侧实际张力值T1，求得扣索锚固端应力损失值FW，即FW=T2-T1；测量人员利用全站仪测定扣索与扣索鞍接触面圆弧度值θ；根据式（12）得到扣索鞍摩阻系数f测定值。

（2）校验：通常拱桥施工中，扣索与扣索鞍通常沿塔架竖直方向独立布置多组，且结构组成形式相同，故可测定同一施工现场另一组结构组成形式相同的扣索与扣索鞍组合的T1值与θ值，并结合f测定值反算得到FW计算值，同时测定该组扣索T2值得到FW实测值，将FW计算值与FW实测值进行比较，若误差在合理范围内，则认为f测定值准确。

（3）复验与应用：通常在施工前，T1值是设计方提供的现有标准值，T2值需要施工方利用穿心千斤顶等设备在扣索张拉端一侧进行施加，同时扣索鞍处应力损失FW值未知，故究竟应该在扣索张拉端一侧将T2值施加至多大是一个现实的技术难题。根据式（12），当某一拱桥缆索吊装结束后，同批已知准确f值的扣索鞍周转至下一类似工程利用时，利用上述校验的方法对f值进行复验，若复验通过，则可将f值应用在计算该桥其他结构形式相同扣索索鞍处的FW值及T2值。

2 算例验证

2.1 测定与校验算例

平南三桥为中承式钢管混凝土拱桥，大桥全长为1 035 m，主桥跨径为575 m。大桥采用缆索吊装法进行施工，塔架采用“吊扣合一”设计。施工中，沿塔架竖直方向从下至上共计设置11道扣索与扣索索鞍组合，其中1#～5#扣索索鞍采用单滑轮式，6#～11#扣索索鞍采用滑轮组式，扣索均采用同材质12 mm钢绞线组，扣索索鞍的设计参数及计算简图分别见表1与图5。

根据算例1提到的2类扣索索鞍结构形式，设置2组计算对象：（1）选取塔架3#扣索鞍及扣索组合测定单滑轮式扣索索鞍摩阻系数，以塔架5#扣索索鞍及扣索组合对其进行校验；（2）选取塔架8#扣索索鞍及扣索组合测定滑轮组式扣索索鞍摩阻系数，以塔架10#扣索索鞍及扣索组合对其进行校验。施工现场利用全站仪测定扣索索鞍θ值，利用绳索张力计测定扣索的T1值与T2值。扣索安装完成且在其张拉端利用穿心千斤顶分6次施加张力至张拉控制应力，本研究以此6个工况利用式（12）分别求得的f值，并以f的算术平均值作为其测定值，见表2。

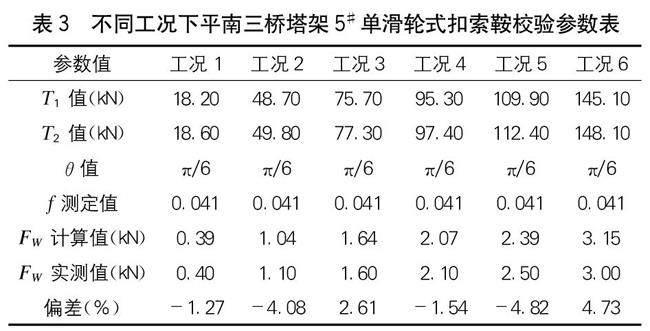
根据表2，不同索力荷载工况下塔架3#扣索索鞍的摩阻系数算术平均值为0.041，故以此值作为单滑轮式扣索索鞍摩阻系数f的测定值。测得塔架5#扣索索鞍及扣索组合不同工况下的T1值与θ值，并与f测定值一同带入式（12），计算得到FW计算值，见表3。

由表2及表3可见，塔架3#扣索索鞍与5#扣索索鞍均为结构形式与尺寸相同的单滑轮式索鞍，以塔架3#扣索索鞍及扣索组合为对象计算得到的摩阻系数测定值作为塔架5#扣索索鞍处应力损失值的计算参数，通过式（12）反算得到的不同工况下5#扣索索鞍处应力损失计算值与实测值的偏差均＜5%，偏差最大值仅为4.82%，说明式（12）对于计算单滑轮组式扣索索鞍的摩阻系数来说具有较高的准确性。同时，塔架5#扣索索鞍与其扣索接触面弧度值较5#扣索索鞍与其扣索接触面弧度值小，故扣索在5#扣索索鞍处的应力损失百分比更小。

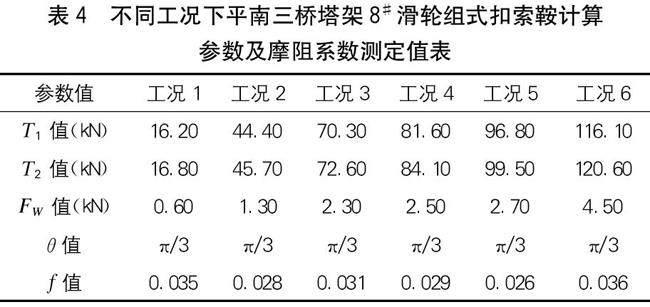
现以8#与10#扣索索鞍及扣索组合为对象，测定滑轮组式扣索索的摩阻系数，并进行校验，见表4和表5。

根据表4可知，相同应力分级工况下，滑轮组式扣索索鞍处的摩阻系数较单滑轮式扣索索鞍小25%左右，说明滑轮组式扣索索鞍的工程实用性更加优越。不同索力荷载工况下塔架8#扣索索鞍的摩阻系数算术平均值为0.032，故以此值作为滑轮组式扣索索鞍摩阻系数f的测定值。以塔架10#扣索索鞍及扣索组合作为计算对象进行校验，见表5。

由表4及表5可知，通过式（12）反算得到的不同工况下10#扣索索鞍处应力损失计算值与实测值的偏差均＜5%，偏差最大值仅为4.65%，说明式（12）对于滑轮组式扣索索鞍摩阻系数的计算同样适用。另外，由于θ值的不同对索鞍处应力损失造成的影响规律与单滑轮式扣索索鞍的规律一致。

2.2 复验与应用算例

新圩红水河特大桥为中承式钢管混凝土拱桥，大桥全长为523 m，主桥跨径为354 m。大桥采用缆索吊装法进行施工，塔架采用“吊扣合一”设计。施工中，沿塔架竖直方向从下至上共计设置7道扣索与扣索索鞍组合，其中1#～3#扣索索鞍采用单滑轮式，4#～7#扣索索鞍采用滑轮组式，扣索均采用同材质12 mm钢绞线组。大桥于2022年5月进行塔架安装施工，塔架扣索索鞍均从平南三桥转场使用，未另行加工，2类索鞍的材料特性、结构形式与尺寸与平南三桥相同。

现根据该桥施工现场的实测数据及上文提到的校验方法对转场使用的2类索鞍摩阻系数进行复验：（1）选取塔架2#扣索鞍及扣索组合作为单滑轮式扣索索鞍摩阻系数的复验对象；（2）选取塔架6#扣索索鞍及扣索组合作为滑轮组式扣索索鞍摩阻系数的复验对象。需要注意的是，该桥施工中扣索安装完成且在其张拉端利用穿心千斤顶分4次施加张力至张拉控制应力，这里与平南三桥的应力分级工况有所区别。复验情况见表6和表7。

由表6及表7可见，以不同大桥工程为依托，利用2类扣索索鞍摩阻系数测定值分别计算得到的对应索鞍处应力损失计算值与实测值的偏差均＜5%，说明索鞍在保持完好的周转使用过程中，其摩阻系数是定值，并不会随着工程环境的不同而改变，从而证明了式（12）的正确性和普适性。复验结果说明，只要一批次结构形式、材料特性与尺寸相同的扣索索鞍未发生损坏，无论其周转至任一大桥工程进行使用，利用其已测定的摩阻系数计算得到的应力损失值和扣索张拉端的应力控制值，均具有极强的工程应用性。

3 结语

本文从基本数学微分原理出发，结合施工现场扣索索力监测数据，计算得到了拱桥施工塔架扣索索鞍摩阻系数的计算公式，并以平南三桥与新圩红水河特大桥作为实例依托，分别通过对2类摩阻系数的测定、校验、复验及应用4个步骤证明了计算公式的准确性和普适性。经过本次研究，可以得到如下几点结论：

（1）单滑轮式与滑轮组式扣索索鞍摩阻系数f可以表达为扣索与扣索索鞍接触面合摩阻力FW、扣索锚固端一侧张力值T1、扣索与扣索鞍接触面圆弧度值θ三者之间的函数关系。

（2）分别以平南三桥塔架3#与8#扣索索鞍与扣索为组合对象，计算2类扣索索鞍摩阻系数，单滑轮式扣索索鞍计算平均值（测定值）为0.041，多滑轮式扣索索鞍计算平均值（测定值）为0.032。分别以5#与10#扣索索鞍与扣索为组合对象，校验了2类扣索索鞍摩阻系数测定值，得到2类扣索索鞍校验结果平均偏差均＜5%。以上说明利用式（12）计算得到的摩阻系数具有较高的准确性。

（3）鉴于新圩红水河特大桥塔架扣索索鞍均从平南三桥转场使用，故以新圩红水河特大桥为依托对2类扣索索鞍摩阻系数进行了复验。结果表明，2类扣索索鞍若材料特性、结构形式与尺寸相同，且不发生损坏的前提下进行周转使用，其摩阻系数不会因工程环境的更新而发生改变，证明式（12）具有较强的工程普适性。

（4）经过计算，发现相同应力分级工况下，滑轮组式扣索索鞍处的摩阻系数较单滑轮式扣索索鞍小25%左右，说明滑轮组式扣索索鞍的工程实用性更加优越。

参考文献

［1］罗小斌，秦大燕，杜海龙，等.塔架扣索鞍轮摩阻系数试验研究［J］.公路，2020（5）：116-120.

［2］刘佳辉.矮塔斜拉桥弧形索鞍区钢绞线拉索抗滑移性能试验研究［D］.重庆：重庆交通大学，2022.

［3］王 路.悬索桥主缆与索鞍间滑移机理理论及试验研究［D］.成都：西南交通大学，2018.

［4］贺拴海，陈英昊，李 源，等.考虑摩阻力影响的悬索桥索鞍精确算法［J］.长安大学学报（自然科学版），2019，57（2）：57-64.