基于物理信息神经网络的波动方程优化求解方法
吴丹澜 梁展弘 余懿 蔡博 郑邦宏 王梓超 张紫玲
关键词:物理神经网络;机器学习;波动方程;救援;物理学
0引言
在当今社会,由于全球气候变化、生态环境破坏以及地壳运动活跃等因素的影响,自然灾害[1]的发生呈现出频次增加、强度加剧的趋势,包括地震[2]、洪水、台风、滑坡、森林火灾等多种灾害形式。这些灾害不仅对人民生命财产安全构成严重威胁,而且对社会稳定和经济发展也带来了巨大挑战。因此,在灾后救援工作中,如何快速、精准地定位被困人员,提升伤员搜救效率,最大限度地减少因灾害造成的人员伤亡和经济损失,成为一个紧迫且重要的课题。
为实现这一目标,国家救援队伍积极采用先进的科学技术手段,其中声波类探测仪器在救援现场的应用发挥了关键作用。这类仪器通常利用超声波、地震波等物理原理,通过发送声波并接收其反射信号来判断废墟下是否存在生存空间及生命迹象。它们能够在复杂的环境下穿透障碍物,帮助救援人员确定被困者位置,极大地提高了搜救工作的成功率。
为进一步提升此类探测设备的效能,科研人员正着重于优化波动方程求解算法的研究与应用。波动方程是描述声波或地震波传播的基本数学模型,其精确求解有助于更准确地模拟现实情况中的声波传播路径和衰减特性,从而提高探测结果的精度。通过深度开发和应用高精度的波动方程[3]数值计算方法,可以显著增强声波类探测仪器的功能性能,使得在面对各类自然灾害时,救援行动能够更加迅速、高效,真正体现“时间就是生命”的救灾原则。
1我国目前的救援能力现状
随着全球气候变化和人类活动的不断增加,自然灾害的发生频率和规模也在不断扩大,而我国也面临着越来越严峻的救援挑战。
一般来说,在事故发生后,救援队伍会立刻投入救援当中,但因被困人员一般被埋在数米厚的泥土下,导致搜救工作面临着巨大困难。而此时生命探测仪器则成为不可或缺的救援工具,像遇到滑坡、地震等灾害时,救援人员通常难以凭肉眼判断被困人员的具体位置,但活着的人都有生命特征,身体会有温度、呼吸、心跳,会产生二氧化碳气体,而这些就是生命探测仪器判断幸存者位置的依据。
针对不同体征,生命探测仪[4]可分为声波探测仪、雷达探测仪、红外探测仪、光学探测仪等不同种类。但这些装备也有其局限性,如声波探测仪无法区分人和其他动物,且会受到噪声等干扰。
在声波探测仪[5]中,捕获声波的震动通过波动方程去解析出是否为幸存者心跳、呼吸、移动等发出的微弱声音,波动方程解的精确程度即可影响到仪器的精准程度,改进波动方程可以从软层面提高仪器的精确度。除此之外,改进波动方程也可以增加仪器对干扰声波的抗干扰能力。生命探测仪的普及应用不断扩大,显著提升了搜救工作的速度、准确性以及安全性。与此同时,中国积极推动国家救援体系[6]的完善,加强了紧急救援装备的建设。
1.1声波检测仪
在灾害救援中,声波检测仪器以其无损、快速、准确的探测能力,为救援人员提供了重要的生命迹象信息和灾害现场的详细情况。
首先,声波检测仪器通过发出声波并接收反射回来的声波,能够探测到被掩埋或困在废墟下的人员。
这种仪器能够穿透混凝土、土壤、水等介质,为救援人员提供被困人员的准确位置信息,从而加快救援速度,减少救援人员的盲目挖掘和搜寻时间。
其次,声波检测仪器还广泛应用于灾害现场的结构安全监测。在地震、泥石流等灾害发生后,建筑物和桥梁等结构可能存在安全隐患。声波检测仪器通过检测结构内部的损伤和裂缝,能够评估结构的稳定性和安全性,为救援人员提供重要的决策依据。
而波动方程作为描述声波传播的基础理论,对于理解和优化声波检测仪的性能至关重要。通过深入研究波动方程及其在声波传播中的应用,可以不断优化声波检测仪的性能,为灾害救援工作提供更准确、可靠的技术支持。
2波动方程
2.1波动方程概念
波动方程或称波方程(WaveEquation)是一种描述自然界中各种波动现象的二阶线性偏微分方程,主要描述自然界中的各种波动现象[8],例如机械波,包括声波、光波、引力波、无线电波、水波、和地震波[9]等。波动方程抽象自声学、波动光学[10]、电磁学、电动力学、流体力学、广义相对论[11]等领域。波动方程的一般形式为:
式(1)中,u是关于位置x和时间t的标量函数,表示波的位移或振幅;v是波的传播速度,是一个常数。
波动方程的物理意义是:任意一点的加速度(即时间的二阶导数)与该点周围的曲率(即位置的二阶导数)成正比,比例系数为波速的平方。这反映了波的传播规律,即波是由局部的振动通过相邻的点的相互作用而向外扩散的。
2.2一般求解波动方程相关方法
波动方程的求解方法有多种,如分离变量法[12]、特征线法[13]、傅里叶变换法[14]等,它们分别适用于不同的方程形式、初始条件和边值条件。
1)分离变量法(SeparationofVariablesMethod)。
分离变量法是一种将偏微分方程化为常微分方程的方法。它的基本思想是将波动方程的解表示为两个或多个变量的函数的乘积,例如y(x,t)=X(x)T(t),然后将这个形式代入波动方程。通过分离变量,得到两个或多个常微分方程,分别求解这些常微分方程,再根据初始条件和边界条件确定常数,最后将各个分量的解叠加得到波动方程的解。这种方法仅适用于齐次边界条件的情况,例如热传导方程、波动方程。
分离变量法的求解缺点是适用范围有限,普适性不强。它不能适用于非齐次边界条件的情况,也难以处理非线性或非均匀的波动方程。
2)特征线法(CharacteristicLineMethod)。特征线法是一种利用波动方程的特征方程来求解的方法。它的基本思想是找出一族曲线,在这族曲线上,波动方程退化为常微分方程。然后在这些曲线上求解波动方程,再将这些曲线上的解拼接起来得到整个区域上的解。这种方法适用于一阶偏微分方程或可以化为一阶偏微分方程的情况,例如波动方程的标准形式uξη=0,其中ξ=x+at,η=x-at。特征线法在非线性以及非均匀的波动方程求解中也存在一些问题,特征线可能会相交或断裂,导致解的不连续或不唯一。此外,特征线法要求初始条件不是沿着特征线给定,否则会导致解的不确定或不存在。对于多维的波动方程,特征线法可能会涉及复杂的边界条件,难以处理。
3)傅里叶变换法(FourierTransformMethod)。傅里叶变换法是一种将偏微分方程转化为代数方程的方法。它的基本思想是将波动方程的解表示为傅里叶级数或傅里叶变换的形式,例如y(x,t)=∫Y(k,t)eikxdk,然后将这个形式代入波动方程。通过傅里叶变换,得到一个关于Y(k,t)的代数方程,求解这个代数方程,再通过傅里叶逆变换得到波动方程的解。
这种方法适用于非齐次边界条件或无穷区域的情况。其缺点是需要对波动方程的解进行傅里叶变换和傅里叶逆变换,这可能会引入误差或失真。对于非线性或非均匀的波动方程,傅里叶变换法可能不适用或难以实现。
3基于PINN的波动方程求解方法
3.1PINN基本原理及求解方法
波动方程是现代科学[15]和工程建设[16]领域中涉及较广的自然物理问题。根据在科学研究和工程建设中的各类初始条件和边界条件,可以将其抽象成以物理信息为特征的偏微分方程[17],并可以通过各类测量检测手段获取偏微分方程中相应的物理数据[18]。这些物理数据信息可以用来训练神经网络[19],从而求解或发现偏微分方程的解或参数。
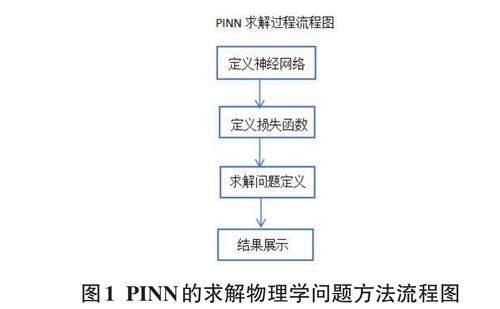
PINN的核心思想是将偏微分方程的形式和参数作为神经网络的一部分,然后通过数据驱动的方式来训练神经网络,使其能够逼近偏微分方程的解,或者发现偏微分方程的参数。PINN可以用来处理一些传统数值方法难以解决的复杂的非线性偏微分方程,或者一些缺乏足够观测数据的反问题。PINN也可以用来探索一些未知的物理规律[20]或现象,从数据中学习出微分方程的形式或系数。该研究基于PINN的求解物理学问题方法流程图如图1所示。
偏微分方程的物理信息可以用来指导神经网络的学习。物理信息的一般表现形式是偏微分方程特征的初始条件和边值条件,以及偏微分方程的某些特殊形式。将偏微分方程的物理信息分为规律信息和数值信息,并提出通过调节不同的训练采样平衡度和训练强度平衡度,以建立具有偏微分方程解的神经网络,最终逼近偏微分方程的所有数值解。
1)PINN深度神经网络架构(DeepNeuralNet?work,DNN)。多层次的神经网络,也称为深度神经网络(DNN),是深度学习的基础,本质上是一种特征学习方法,在自然语言[21]和语音[22]、图像识别[23]、图像和视频数据处理[24]、科学计算等领域效果明显。
神经网络的训练一般使用DNN。DNN通常由多个神经网络层组成,包括输入层、多个隐藏层和输出层。每一层都包含多个神经元,这些神经元通过权重连接形成网络。
在PINN中常用的神经网络是DNN,主要是因为DNN具有灵活性,具有强大的表示学习能力,可以灵活地学习和逼近复杂的非线性映射关系[25]。这使得它们适用于各种不同类型的问题,包括涉及物理方程的问题。DNN能够自动学习数据的特征和模式,而PINN的目标之一就是从数据中学习物理方程。深度神经网络的层次结构使得它们能够逐步提取和组合数据中的抽象特征,有助于更好地捕捉物理规律。在求解一维波动方程的时候证明了DNN的这两个特点,对物理定律的结合也很好,使模型更好地适应真实世界的复杂物理过程。
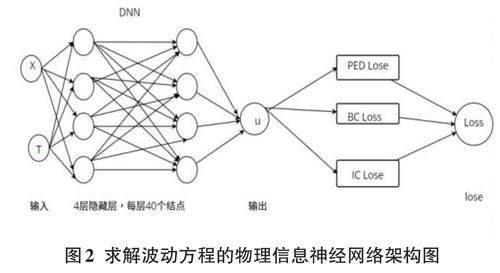
该研究认为波动方程的求解过程如图2所示。架构图的左侧是一个DNN,它由2个输入节点、4个隐藏层和1个输出节点组成。输入节点分别表示波动方程的自变量X和T,分别代表空间和时间。输出节点表示波动方程的因变量u,代表波动的幅度。隐藏层是由40个节点构成的全连接层,每层都使用了RectifiedLinearUnit(ReLU)作为激活函数。ReLU是一种常用的非线性激活函数,使用ReLU的好处是其不存在梯度消失问题,可以提升神经网络的收敛速度,减少参数的相互依赖,缓解过拟合问题。
架构图的右侧是3种不同的损失函数,它们分别表示波动方程的物理约束[26]。PartialDifferentialEquationLoss(PEDLoss)表示偏微分方程的损失,它衡量了DNN输出的U是否满足波动方程的形式。BoundaryConditionsLoss(BCLoss)表示边界条件的损失,它衡量了DNN输出的U是否满足波动方程的边界条件。InitialConditionLoss(ICLoss)表示初始条件的损失,它衡量了DNN输出的U是否满足波动方程的初始条件。这三种损失函数都是基于平方误差的,它们的和构成了总的损失函数,用于优化DNN的参数。最后通过数据驱动方式训练神经网络,实现损失函数输出值的最小化。
2)波动方程代入PINN。在PINN中,物理方程通常被嵌入神经网络的训练过程中,以提高模型对物理系统行为的理解。根据以上论述,将波动方程代入PINN进行求解的步骤主要体现如下。
将式(1)波动方程的方程形式、规律信息和数值信息,构建一个神经网络,将该神经网络的空间坐标定义为x和时间t为输入,将输出波函数的估计值u?(x,t)作为神经网络的输出,然后将波动方程作为损失函数的一部分。该损失函数包括波动方程的结构损失、边值条件损失、初值条件损失和真实数据条件损失。波动方程对应于时间二阶导数和空间二阶导数,如式(2)所示:
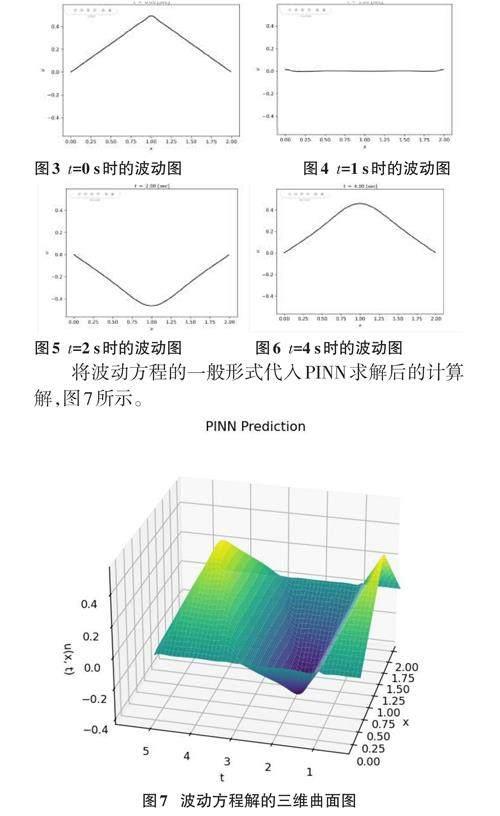
随后,需要收集有关系统行为的数据,包括边界条件和初始条件,并将这些数据运用到梯度下降或其他优化算法以实现最小化损失函数,从而调整神经网络的参数,得到波动方程最逼近的解。在这个过程中,需要用真解去验证PINN的解集是否正确,由于真解表示波动方程u在空间x和时间t上的变化,在几个时间戳上进行说明,分别是t在初始状态、1s、2s、4s时的状态,可以看到u的波形如图3~图6所示。
将波动方程的一般形式代入PINN求解后的计算解,图7所示。
其中,?2u为关于空间?x2和时间?t2的解函数。
波动方程描述了一维空间中的波动现象,其中u(x,t)是波函数,表示波动在空间x和时间t上的变化。该方程表达了波动的传播速度v对波动的空间和时间演化的影响。在常规波动方程的求解过程中,深度神经网络(DeepNeuralNetwork,DNN)的任务是学习函数u(x,y),使其满足上述波动方程,并同时满足初始条件和边界条件。通过优化神经网络的参数,使得输出的解尽可能地逼近真实的波动方程解。在图7中,可以看出PINN解在t=0,1,2,4时的波形u(x,y)跟真解上对应时刻的u的波形形状是拟合的,说明PINN的训练效果和结果都是正确的。
3.2波动方程代入PINN实验调试分析
波动方程是描述波动现象的一种偏微分方程,在改良声波应用上有很大的作用。根据上述解波动方程的理论,可以将其中的方程代入为声波方程,声波神经网络的训练过程等同于声波传播[27]的反问题。在地球物理学中,通过在地表激发地震波、记录相应的地震响应信号、建立反问题模型并数值求解该问题来确定地下结构的属性。在声波神经网络中,给定输入和输出层条件后,神经网络反问题的求解可以确定网络结构权重系数[28],这些系数的数量通常非常庞大[21]。根据声波方程的特点修改其初始条件和边界条件,将物理方程修改为声学方程,确保正确计算声学方程的各个导数,并设置符合声学问题求解需求的损失函数。
在实验过程中,本研究添加了0.05的噪声模拟真实数据,然后构建神经网络,定义损失函数,计算离散点之间的间隔,使用中心差分法计算偏导数和二阶偏导数,将得到的近似导数与声波方程进行比较,最后输出结果。在图8中可以看出三个损失函数的折线图现象。在相同条件下,初始条件(IC)、边界条件(BC)、偏微分方程(PDE)三个损失函数的数据集数越多,则误差越小,当超过10000个例子时,误差快速下降。
调整神经网络的结果,使其更好地拟合声波方程,需要根据实际情况调整优化器和超参数,以及训练时长和迭代次数,从而完成从波动方程到声波方程的替换。
在实际实验中,调试神经网络时选择合适的隐藏层和每层的神经元个数非常重要。这个过程需要不断调试,并需要大量数据进行调整,以获得理想的误差值。在声波方程替换波动方程中,最困难的部分是修改边界条件,因为需要针对不同的场景进行不同的边界修改。这是未来的研究方向,即如何自适应地确定边界条件。另外,由于边界条件的影响,即使方程解的误差很小,最终生成的解集也可能与实际解不对应。表1显示了神经网络调试数据。
ICLoss(初始条件损失)表示神经网络在模拟系统初始状态(t=0时刻)时的误差,通过比较神经网络在初始时刻的位移与真实初始条件值之间的均方误差来计算。
BCLoss(边界条件损失)表示神经网络在边界上满足约束条件的程度,通过比较神经网络在给定空间和时间边界上的位移与真实边界条件值之间的均方误差来计算。
PDELoss(偏微分方程损失)表示神经网络在偏微分方程上的拟合误差,即在系统内部满足物理方程的程度,通过比较神经网络在随机采样点上满足偏微分方程的程度,即通过比较波动方程的时间和空间偏导数之间的均方误差来计算。
这三个损失项的综合构成了总体的损失函数(Loss)。通过最小化这些损失,优化算法试图调整神经网络的参数,使其能够较好地逼近真实的波动方程解并满足初始条件、边界条件和偏微分方程。表中显示误差值都很小,但对于方程解来说,误差肯定是越小越好。经过不断尝试,发现当DNN的隐藏层数量为5,神经元数量为50时,取得的误差最小。
4结论
该研究提出了物理信息神经网络(PINN)应用于波动方程求解的方法,降低了波动方程应用的难度。在解波动方程的过程中,该研究尝试将其应用于声波方程,并通过数值算例表明,波动方程在解决声波问题上发挥着重要作用。研究也证明了深度神经网络(DNN)在物理信息神经网络中的应用具有灵活性和广泛性。通过调整隐藏层的层数和神经元个数,可以使方程的解集拟合。然而,训练过程中可能导致过度拟合,使得解无法形成。因此,在调试过程中,ICLoss、BCLoss和PDELoss之间存在最优权衡。
在波动方程中,PDELoss的影响相对于其他两个损失更为显著。因此,在调试的过程中,着重调节了PDELoss,以达到总损失的最小值。实验中发现,当DNN的隐藏层数量为5,神经元数量为50时,取得的Loss最小,对于提高波动方程求解精度具有重大意义。相比波动方程的传统解法,这一方法有着显著的改进。然而,受到边界条件影响,声波方程[29]的图形与真解的对应关系存在一定问题。因此,边界条件的自适应修改仍然是未来研究的重要技术方向。
未来的深入研究将集中在进一步优化物理信息神经网络在波动方程中的真实数据应用上,特别是在边界条件[30]的自适应和误差最小化方面。此外,还将探索这些网络在处理更复杂的偏微分方程中的更具体应用,希望通过持续创新和突破,为社会安全和应急救援响应能力的提升做出更大的贡献。

