双层空竹超表面中基于 BIC 的局域太赫兹磁场增强的研究

阎晓娜 高新卓 刘馨怡 金钻明

摘要：设计了包含双层空竹的超表面，通过调节其晶格周期实现了不同阶晶格模式与超表面本征模式间的耦合，获得了3个强耦合区，并在两个晶格周期处实现了弗里德里希–温特根型连续域束缚态（Friedrich-Wintgen bound states in the continuum ，FW-BIC）。基于耦合模理论对其进行分析，理论分析结果与模拟结果吻合，进一步证明了结构的有效性。讨论了在介质间隔层中基于强耦合和 FW-BIC 的局域磁场增强，发现最大磁场强度是入射太赫兹波磁场强度的41209倍，且该值是单纯的由超表面电磁共振产生的磁场强度的4倍。这项研究将为强场太赫兹产生和太赫兹非线性研究提供参考。

关键词：超表面；强耦合；连续域束缚态；耦合模理论；磁场增强

中图分类号： O 441 文献标志码： A

Research of BIC-based localized terahertz magneticenhancement in double-layered diabolo metasurface

YAN Xiaona1，GAO Xinzhuo1，LIU Xinyi1，JIN Zuanming2

（1. College of Science， Shanghai University， Shanghai 200444， China;

2. School of Optical-Electrical and Computer Engineering， University of Shanghai forScience and Technology， Shanghai 200093， China）

Abstract： Ametasurfacecomposedofstackeddouble-diabolostructurewasdesigned. By adjusting lattice period of the metasurface， hybridization between different order lattice modes and eigenmodes of the metasurface led to three strong coupling regions and two Friedrich-Wintgen BIC （FW-BIC） at two lattice periods. The analysis results based on the coupled mode theory agreed well withthenumericalsimulation，whichfurtherprovedthevalidityofourstructure. Thestrong coupling and BIC effect could be used to enhance localized magnetic field in spacer layer. The maximum magnetic field intensity was 41209 times of the incident THz wave， and this value was 4 times comparing with the purely electromagnetic resonance of metasurface. The results provide suggestions for the study of strong field THz generation and THz nonlinear optics.

Keywords： metasurface; strong coupling; bound states in the continuum; coupled mode theory;magnetic field enhancement

引言

随着太赫兹科学技术的发展和成熟，太赫兹波被广泛应用于安全检测、疾病诊断、通信和国防等领域。然而，由于自然界中缺乏天然响应的太赫兹材料，强场太赫兹器件的发展仍受到限制。超材料是人工设计的亚波长微结构材料，通过对微结构单元设计，超材料能够实现任意的介电常数和磁导率，从而为灵活调控电磁波提供了可能。太赫兹超材料的出现为制备太赫兹功能器件，进而有效调控太赫兹波提供了解决方案。

衡量强场太赫兹器件性能的指标之一是需具备光场束缚能力，从而增强光与物质的相互作用，因此在太赫兹超材料的设计中需引入光场束缚机制以获得强太赫兹场。连续域束缚态（boundstates in the continuum， BIC）是一种光与物质之间的强相互作用，具有强束缚和超高品质因子等特性，在窄带滤波、传感、成像和非线性光学等领域均有应用[1-4]。近年来，基于超材料和超表面的 BIC 被提出并用于电磁波调控。理想的 BIC 具有无限大的寿命和零泄漏，在电磁谱中是观察不到的。但是在产生 BIC 的超表面中引入结构扰动，就可以在远场中观察到准 BIC。在实际的光学设计中，根据扰动的不同，光学 BIC可分为两类：分别是对称保护型 BIC（ symmetry- protected BIC ， SP-BIC）和偶发型 BIC 。SP-BIC 是通过打破结构对称性或倾斜入射来实现的[5]；而偶发型 BIC 中的共振耦合型 BIC 是在保持结构对称性的情况下，通过调整系统参数使束缚态与连续域之间的耦合消失来实现的[6]，包括法布里–珀罗型 BIC（Fabry-Pérot BIC，FP-BIC）[7]和弗里德里希–温特根型 BIC（Friedrich-Wintgen BIC ， FW-BIC）[8]。其中，FW-BIC 通常由两种不同激发模式在满足相位匹配条件下通过相消干涉产生的，其辐射通道伴有明显的反交叉现象。近年，关于 FW-BIC 的研究引起了人们广泛的兴趣，如 Azzam等[9]探讨了在由银光栅和介质层组成的超材料中，基于光子波导模式与光栅中等离激元的耦合实现的 FW-BIC 。Niu 等[10]设计了包含两个共面的金属开口环谐振器的太赫兹超表面，通过调节内环参数使内外两环支持的 LC 模式和四偶极模式耦合，获得了 FW-BIC 。Li 等[11]将石墨烯引入金属太赫兹超表面中，实现了准 BIC到 BIC 的动态切换。 Gao 等[12]设计了由石墨烯光栅和石墨烯薄片组成的超表面，基于法布里–珀罗共振模式和波导模式之间的相消干涉实现了 FW-BIC，并用于完美吸收。 Zhao 等[13]设计了能同时支持 LC共振模式和偶极共振模式的金属太赫兹超表面，实现了 FW-BIC，并讨论了其在太赫兹电、磁场增强方面的应用。由前述可知，对利用 FW-BIC 实现太赫兹波段电磁场增强的讨论较少，且缺少对利用晶格模式与超材料本征模式之间的耦合实现 FW-BIC 的讨论。晶格模式（lattice mode， LM）[14]是一种沿着金属–电介质界面传播的表面模式，它的能量强烈集中在界面而不会辐射到远场，因此当晶格模式与其他模式耦合时可以有效减少模式的辐射损失，从而增强品质因子（Q 因子），如 Luo等[15]利用晶格增强了准 anapole 模式的 Q 因子，并用于太赫兹免疫传感器。晶格模式与超材料本征模式耦合时的强耦合作用也为实现 FW-BIC 和超强电磁场提供了可能。

本文设计了一个包含双层空竹的超表面结构，通过调整晶格周期实现了不同阶的晶格模式与本征模式间的强耦合，在相位匹配条件下，实现了 FW-BIC，并讨论利用 FW-BIC 和强耦合效应来实现太赫兹波段的磁场增强，发现相对于入射太赫兹波，最大的磁场强度可提高4个数量级。

1 双层空竹超表面的设计及本征模式

具有 C2旋转对称性的双层空竹超表面如图1（a）所示，其中50?m厚的本征硅作为基底，在其顶部沿垂直方向沉积两层结构相同，周期性排列的200 nm厚的金空竹阵列结构，两层金属阵列由2?m厚的介质层（聚酰亚胺）分开。在模拟中，金为有损金属，电导率σ=4.561×107 S/m。图1（a）还给出了一个结构单元的正视图及其几何参数，其中 L =100μm ，l =20μm ， a（x;y）= a（4，4）μm ，结构沿 x 轴和 y 轴的晶格周期分别用Px和Py表示。为了在超表面中激发本征模，设入射太赫兹波的偏振沿 x 轴方向。

为体现双层空竹超表面在磁场增强方面的优势，图1（b）给出了当Px = Py =110μm 时，利用 CST 模拟的单层和双层空竹超表面的透射谱。其中单层空竹超表面（仅由衬底和单层空竹结构组成，未画出）的透射谱只有一个本征模式，共振频率在0.48 THz，谱线较宽，辐射损耗大。而对于双层空竹超表面则包括两个本征模式——对称模式（ symmetric mode，SM）和反对称模式（anti-symmetric mode， ASM），它们是由上、下两个空竹结构的杂化耦合激发的。其中， SM 的共振频率为0.44 THz，谱线较宽，但比单层空竹超表面的窄，并具有平行的表面电流分布，如图1（c）中上方的图所示，SM 也称为电模式。由于 SM 中两个电偶极子的强度不同，它们将形成辐射通道，导致 SM 具有较低的电场限制能力。ASM 的共振频率为0.69 THz，线宽较窄，具有不对称的 Fano线形和反平行的表面电流分布，如图1（c）中下方的图所示。根据安培定则，磁场将限制在中间介质层内，因此 ASM 也称为磁模式。多模共振的产生为研究不同模式间的耦合，进而实现 FW-BIC 提供了可能。

超表面中的周期性结构可以产生沿表面传播的晶格模式，其共振频率可以由晶格周期Px和Py调控。在正入射情况下，晶格模式的共振频率表示为[14]

fLM = i22+ j22 （1）

式中： c 是真空中的光速；neff是晶格模式所在的传播介质的有效折射率；（i，j）是定义晶格模式阶数的一对非负整数。

调节晶格周期，当晶格模式的共振频率接近超表面本征模式的共振频率时，两个模式之间将发生耦合，耦合程度由二者间的频率失谐决定，这意味着晶格模式可以选择性地增强或抑制其中的本征模式。下面将讨论不同阶的晶格模式与本征模式间的耦合特性。

2 超表面中晶格诱导的强耦合和FW-BIC

众所周知，FW-BIC 源于两个不同性质的共振的相消干涉，在所设计的超表面结构中，两个相互耦合的共振模式是晶格模式和超表面结构的本征模式，包括 ASM 和 SM。为了系统地阐述两共振模式之间的相互作用及其受晶格周期的影响，给出了当晶格周期Px = Py = P，以步长10μm，从110μm增加到300μm 时超表面的透射谱，见图2。可以看出，随着晶格周期的增加，两个晶格模式 LM 1和 LM 2逐渐接近本征模式并与之耦合。

在研究模式耦合之前，先判断 LM 1和 LM 2的阶数。图3（a）为晶格周期 P=110μm 时 LM 1和 LM 2在xOy平面上的电场分布，显然，它们的电场不仅分布在谐振器的非金属区域，还延伸到相邻谐振器。在 LM 1中，表面波仅沿 x 轴方向传播， LM 1为（±1，0）阶晶格模式；在 LM 2中，表面波在整个介面上延伸，并且产生对称、周期性的场分布， LM 2为（±1，±1）阶晶格模式。根据式（1），在相同的晶格周期下， LM 2的谐振频率高于 LM 1。图3（b）表明，两个晶格模式在空竹对上均具有平行的表面电流分布。

图2中的透射谱表明，一个晶格模式和一个本征模的耦合会导致杂化分裂，产生两个杂化模式：高频杂化模式（high frequency hybrid mode，HFHM）和低频杂化模式（low frequency hybridmode， LFHM）。值得注意的是，当晶格周期分别为159μm 和220μm 时，两个低频杂化模式完全消失，形成两个具有无限寿命和零线宽的暗模式，在透射谱上表现为平滑的谱线，这表明了 FW-BIC 的形成，分别用 BIC 1和 BIC 2来表示。

为了观察 FW-BIC 的形成过程，图4（a）给出透射谱随晶格周期 P 的变化图像。其中，未发生耦合时，本征模式（SM 和 ASM）和晶格模式（LM 1和 LM 2）的共振频率曲线分别用虚线和实线表示。当本征模式和晶格模式耦合时，会观察到3个共振反交叉区域，分别来自于 LM 1与 ASM ，LM 2与 ASM ，LM 1与 SM 之间的耦合，共振反交叉的出现说明每两个模式之间发生了强耦合。同时，在两个特定的晶格周期159μm 和220μm处，3个低频杂化模式中的两个消失，这是 FW-BIC 形成的典型特征。因为在调节晶格周期时，结构的对称性始终保持不变，所以 BIC 1和 BIC 2形成的原因是在相位匹配条件下， LM 1和 LM 2分别与 ASM 发生相消干涉。图1（c）和图3（b）也显示， ASM 与 LM 1，ASM 与 LM 2分别具有反相电流分布。在这两个特定周期处，每两个模式之间的耦合使电流不仅反相而且强度相同，因此发生相消干涉。偏离这两个特定周期值，两个模式之间的耦合程度发生变化，从而低频杂化模式的辐射阻尼和线形变化，导致不同泄漏度的准 BIC 产生。另一方面，SM 与 LM 1具有同相的表面电流分布，是相长干涉，因此 SM 与 LM 1耦合时没有 BIC 产生。

实际上，共振线宽消失会导致无显著的光谱特征显现，理想的 BIC 是不可观测的。评估BIC 性能的一般策略是追踪准 BIC 的品质 Q 因子的发散轨迹[16]。Q 因子的值定义为 Q =！0/2γ ，其中！0是谐振频率，γ是谐振的辐射和非辐射阻尼率[17]。在发生 BIC 的晶格周期附近的两条低频杂化模式谱线的 Q 因子随晶格周期的变化如图4（b）和（c）中的蓝色菱形虚线所示。结果表明，当晶格周期调整到特定值（对于 BIC 1，P =159μm；对于 BIC 2，P =220μm）时，线宽完全消失，导致 Q 因子发散；当晶格周期偏离这两个特定值时， Q 因子逐渐减小，且 BIC 变为准 BIC。对于理想的 BIC，理论上的 Q 因子应接近于无穷大，然而，由于金属的固有欧姆损耗和金属超表面的辐射损耗，导致实际 Q 因子是有限的。因此，图4（b）和（c）中的红线给出了当使用完美电导体（perfect electric conductor ，PEC）替换双层空竹超表面中的有损金属金，以忽略欧姆损耗时的 Q 因子。显然，忽略金属超表面的固有损耗可以显著提高准 BIC 的共振 Q 因子。然而，在 PEC 超表面中， BIC 出现在两个新的晶格周期处，分别为 P=153μm和217μm，这些周期值与有损金属超表面相比略有偏移，但所涉及的耦合机制是相同的。

由于高 Q 共振通常伴随着低的共振强度 I，因此通常引入另一品质因数 FOM 来权衡 Q 因子和共振强度，其值 Fm= Q × I [18]。图4（d）显示了金属超表面中各准 BIC 的 FOM 值。结果表明，BIC 1和 BIC 2附近的最大 FOM 值分别出现在晶格周期 P =180μm 和240μm处，其值分别为13.19和15.46。

3 基于耦合模理论的 FW-BIC

晶格模式和 ASM 之间强耦合产生 BIC 也可以从时域的耦合模理论（coupled-modle theory，CMT）分析，为了分析方便，针对 PEC 超表面进行讨论。

对于无损 CMT 模型，两模式耦合两端口系统的响应可以表示为[13]

式中：[a1; a2]T 为两模式（晶格模式和 ASM）的共振幅度；！1（γ1）和！2（γ2）分别是两模式的共振频率（辐射损耗）；j 是复数且满足 j2=-1；κ表示两模式间的耦合强度；γ12（=γ21）是阻尼产生的耦合系数，由于系统的对称性，γ12=γ21= pγ1γ2；κij是模式i和端口 j （i; j 2{1;2}）之间的耦合系数； s1+和 s2+分别是端口1和端口2的入射波幅度。激发的共振模式的出射波为

式中： s1-和 s2-分别是端口1和端口2的出射波幅度；rd和 td 是在没有谐振模式情况下端口之间的直接反射和透射系数，对于一般的超表面rd =0 ， td =1，而对于互补型超表面rd =1 ， td =0；dij是端口j 和模式i之间的耦合系数（i; j 2{1;2}）。根据能量守恒可以得到κ11=κ21= d11= d21= pγ1和κ22=κ12= d22= d12= pγ2。如果入射波从端口1入射，求解式（2）和式（3），得

及端口2的出射波幅度

s2-= tds1+-（ pγ1a1+pγ2a2）

最终得到 PEC 太赫兹超表面的透射谱为

t21= A （s2-/ s1+）

式中， A 是用于调整透射强度的比例参数。

更重要的是，当 Friedrich-Wintgen条件

κ（γ1-γ2）= pγ1γ2（！1-！2）（8）

被满足时，系统哈密顿矩阵的其中一个本征值变为纯虚数，这意味着该特征模将成为辐射损耗为

零的 FW-BIC。

在 CMT 的框架内，首先固定ω2=0.69 THz ，阻尼率γ1 ，γ2和耦合系数κ， 然后针对不同的晶格周期来调整ω1的值，透射谱如图5所示，其中蓝色曲线是 CST 模拟的结果，红色曲线是CMT 拟合的结果。从图中可以看到，之前“钝”的准 BIC 曲线由于非辐射损耗的减少而变得“尖锐”了，并且每个周期处两条曲线都完美吻合。

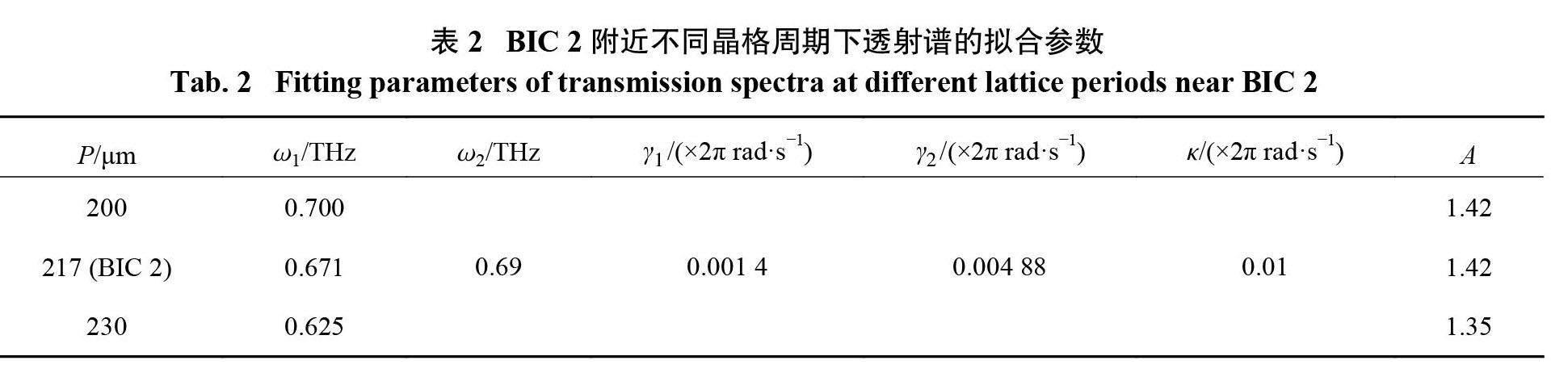
拟合参数的详细数据如表1和表2所示。通过拟合数据分析，可以发现两种耦合模式的辐射阻尼率不相等，若ω1=ω2，为使式（8）成立，其中的耦合系数κ应为0，这与第2节讨论的两种模式间存在强耦合相矛盾。共振反交叉点是两个模式共振频率刚好相同的点，这也解释了为什么 FW-BIC 出现在共振反交叉点附近，而非正好落在其上的原因。另外，表2中的γ1要比表1中的小，这是由于高阶晶格模式 LM 2比一阶晶格模式 LM 1具有更强的电磁约束能力而导致辐射阻尼率更低，如图3（ a）所示。同时，由于 ASM 在 BIC 2出现之前已经与一阶晶格模式发生了强耦合，受其共振线窄化的影响，导致拟合数据表2中的γ2值要小于表1中的值。最后， BIC 1对应的耦合系数κ最大，意味着在 ASM 和 LM 1的透射谱中反交叉时拉比劈裂是最大的，这也与图4（a）显示的结果一致。

4 利用强耦合和 FW-BIC 实现太赫兹波段的局域磁场增强

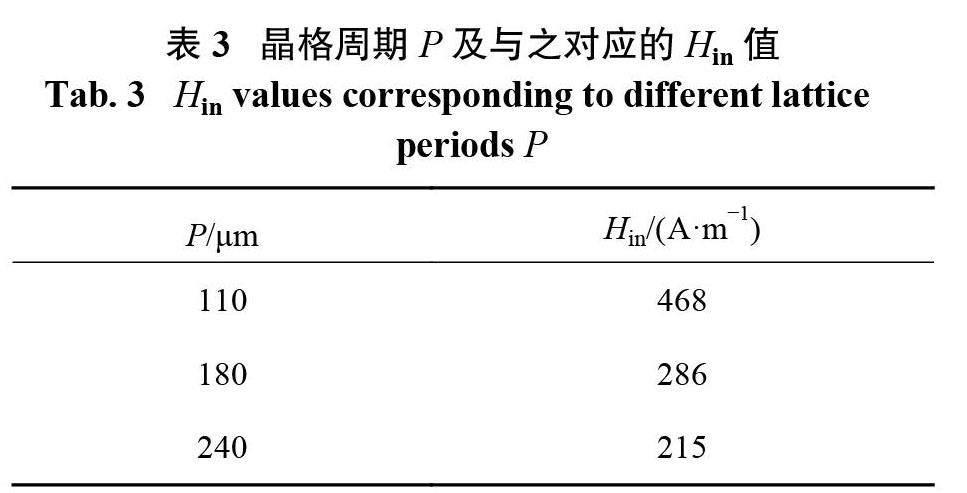
对于单层空竹超表面，两个三角形的连接桥处由于电流聚集，电流密度比其他位置大，因此在桥周围会有局域磁场增强；而对于双层空竹超表面结构，如果上下空竹的表面电流反向，或者电流同向但强度不同，则可以在中间介质层中局域磁场。定义磁场强度增强倍数α=（H / Hin）2，其中 H 和 Hin 分别代表介质中最大的磁场和入射 THz波的磁场分量。关于 Hin 的值需要说明的是：模拟仿真时激励源设置为波导端口，即波导端口为受激端口，其大小要与超材料的晶格周期相匹配，所以晶格周期会影响端口的 E，H 值，即影响 Hin 值。表3给出了本节所涉及的晶格周期及对应的 Hin 值。

图6给出了在晶格周期 P =110μm 时单层空竹超表面中本征模式，双层空竹超表面中本征模式与晶格模式无耦合时两个杂化模式的磁场强度增强倍数。由图可见，在各自的谐振频率处，单层空竹超表面的磁场增强倍数最小，是入射太赫兹波磁场强度的1616倍；而双层空竹超表面中 ASM 的磁场强度大约是 SM 的3倍，分别是入射太赫兹波磁场强度的10404倍和3721倍，且远大于单层空竹超表面的磁场增强。ASM 增强效果强的原因很容易理解，因为在 ASM 中上下空竹有反向电流分布，在介质中的磁场互相增强；而在 SM 中上下空竹的表面电流同向，在介质层中产生的磁场部分抵消。由于双层空竹超表面表现出更优越的局域磁场增强效果，下面将讨论利用 ASM（SM）和晶格模式之间的强耦合实现磁场的进一步增强。

众所周知，对于无损材料，场增强与 Q 因子的平方根成正比。而对于有损材料，由于材料耗散，这个关系并不严格成立，场增强还与共振强度 I 的平方根成正比[19]。因此，有损材料的场增强应与 FOM 值有关。下面，将讨论准 FW-BIC中具有最大 FOM 的晶格周期处的磁场增强。

图7给出了超表面一个单元中上下空竹的表面电流分布以及最大 FOM 所在晶格周期处的磁场强度增强倍数。当 P=180μm（接近准 BIC 1），即 ASM 和一阶晶格模式耦合时，磁场强度增强倍数是25921；而当 P =240μm ，即 ASM和（±1，±1）阶晶格模式耦合时，在准 BIC 2附近的最大磁场强度是入射磁场强度的41209倍，此值是准 BIC 1附近磁场增强的1.6倍。这是因为在 r =240μm 的晶格周期处，耦合发生在 ASM 和高阶晶格模式之间，而高阶晶格模式比一阶晶格模式具有更强的电磁能量限制能力，如图3（a）所示，最终导致更强的辐射抑制和局部磁场增强。另外，对比图6和图7可知，在准 BIC 2附近的最大磁场强度是无强耦合，即只考虑超表面本征共振情况下的磁场增强的4倍，由此说明利用强耦合和 FW-BIC 可以有效增强太赫兹磁场。

由于 SM 与 LM 1之间的强耦合没有产生 FW-BIC ，选择反交叉点处的晶格周期来研究磁场增强。图7最后显示了在 r =240μm 时反交叉点处的最大磁场增强，为27556。该值小于同一周期处 ASM 与 LM 2耦合的结果，这也进一步说明高阶晶格模式诱导的强耦合以及 FW-BIC 的出现可以有效增强磁场。

5 结论

本文设计了一个包含堆叠的双层空竹的太赫兹超表面，通过该结构实现了晶格诱导的强耦合和 FW-BIC，并利用强耦合和 FW-BIC 实现了太赫兹波段局域的磁场增强，获得的最大磁场强度是入射太赫兹波磁场强度的41209倍，且发生强耦合和 BIC 效应时的磁场强度是单纯的超表面电磁共振磁场强度的4倍。本文设计的超表面器件可以用于强场太赫兹的研究中。

参考文献：

[1] FOLEYJM，YOUNGSM，PHILLIPSJD.Symmetry-protectedmodecouplingnearnormalincidencefor narrow-band transmissionfilteringinadielectric grating[J]. Physical Review B， 2014， 89（16）：165111.

[2] ROMANOS， ZITOG， TORINOS，et al. Label-freesensing of ultralow-weight molecules with all-dielectricmetasurfaces supporting bound states inthecontinuum[J]. Photonics Research， 2018， 6（7）：726–733.

[3] TITTL A， LEITIS A， LIU M K， et al. Imaging-basedmolecular barcoding with pixelateddielectricmetasurfaces[J]. Science， 2018， 360（6393）： 1105–1109.

[4] CARLETTI L， KOSHELEV K， DE ANGELIS C， et al.Giantnonlinearresponseatthenanoscaledrivenbyboundstatesinthecontinuum[J]. PhysicalReviewLetters， 2018， 121（3）：033903.

[5] BULGAKOV E N， SADREEV A F. Transfer of spinangularmomentumofanincidentwaveintoorbitalangularmomentumoftheboundstatesinthecontinuum in an array of dielectric spheres[J]. PhysicalReview A， 2016， 94（3）：033856.

[6] GOMIS-BRESCOJ，ARTIGASD，TORNERL.Anisotropy-inducedphotonicboundstatesinthecontinuum[J]. NaturePhotonics， 2017， 11（4）：232–236.

[7] MAKSIMOV D N， BOGDANOV A A， BULGAKOVEN. Opticalbistabilitywithboundstatesinthecontinuum in dielectric gratings[J]. Physical Review A，2020， 102（3）：033511.

[8] KOSHELEV K L， SYCHEV S K， SADRIEVA Z F， etal. Strong coupling between excitons in transition metaldichalcogenidesandopticalboundstatesinthecontinuum[J]. PhysicalReviewB，2018， 98（16）：161113（R）.

[9] AZZAM S I， SHALAEV V M， BOLTASSEVA A， etal. Formationofboundstatesinthecontinuuminhybrid plasmonic-photonic systems[J].PhysicalReview Letters， 2018， 121（25）：253901.

[10] NIU J Q， ZHAI Y Q， HAN Q Q，etal. Resonance-trapped bound states in the continuum in metallic THzmetasurfaces[J]. Optics Letters， 2021， 46（2）：162–165.

[11] LI J T， LI J， ZHENG C L， et al. Free switch betweenboundstatesinthecontinuum （BIC） andquasi-BICsupported by graphene-metal terahertz metasurfaces[J].Carbon， 2021， 182：506–515.

[12] GAO E D， JIN R， FU Z C， et al. Ultrawide dynamicmodulation of perfect absorption witha Friedrich–Wintgen BIC[J]. Photonics Research， 2023， 11（3）：456–462.

[13]ZHAOXG，CHENCX，KAJK，etal. Terahertz investigationofboundstatesinthecontinuumof metallic metasurfaces[J]. Optica， 2020， 7（11）：1548–1554.

[14]TAN T C， SRIVASTAVA Y K， MANJAPPA M， et al. Lattice induced strong coupling and line narrowing of split resonances in metamaterials[J]. Applied Physics Letters， 2018， 112（20）：201111.

[15]LUO C C， CAIWEI T T， FAN Z Y， et al. Terahertz Lattice  enhanced  Quasi-Anapole  Immunosensor assisted by protein antibody and AuNPs[J]. Sensors and Actuators B： Chemical， 2024， 410：135628.

[16]CONG L Q， SINGH R. Symmetry-protected dualboundstatesinthecontinuuminmetamaterials[J]. Advanced Optical Materials， 2019， 7（13）：1900383.

[17] HAN S， CONG L Q， SRIVASTAVA Y K， et al. All- dielectricactiveterahertzphotonicsdrivenby bound states in the continuum[J]. Advanced Materials， 2019， 31（37）：1901921.

[18] TAN T C， SRIVASTAVA Y K， AKO R T， et al. Activecontrolofnanodielectric-inducedTHzquasi-BICin flexible metasurfaces： a platformformodulationand sensing[J].AdvancedMaterials，2021，33（27）：2100836.

[19] HU Z， YUAN L J， LU Y Y. Resonant field enhancement near bound states in the continuum on periodic structures[J]. Physical Review A， 2020， 101（4）：043825.

（编辑：李晓莉）