微专题探究：从“基础模型”走向“复合构建”

［摘  要］ 初中教学中需要引导学生掌握相似三角形知识，形成几何模型，并从知识综合角度适度拓展，形成综合性问题的探究策略. 研究者围绕“8字型”三角形相似模型设计教学微专题，以供研讨.

［关键词］ 相似三角形；“8字型”模型；圆；函数

相似三角形是初中数学教学重点内容，教师需要引导学生归纳三角形相似模型，掌握应用方法，并结合实例指导学生解题. 三角形相似模型有多种，教学探究中建议围绕一种模型深入分析，设置教学环节，逐步深入. 下面围绕“8字型”三角形相似模型设计教学微专题.

三角形相似模型微专题思考

围绕“8字型”三角形相似模型设计教学微专题，教学中教师需要精设环节，引导学生逐步探究. 需注意三点：一是注意环节设计由易到难，逐步深入；二是注意对模型的归纳解读及应用，探究中建议构建“模型解读”，逐步深入“应用探究”；三是模型应用注意结合考查实际，关注知识融合、图形复合.

基于上述三角形相似模型微专题的思考，建议按照如下流程分环节设计教学微专题：

环节一：模型解读，即呈现“8字型”三角形相似的全部模型；

环节二：初步应用，即初步应用模型的性质结论解题；

环节三：深入探究，即开展知识综合应用，结合圆构建复合图形；

环节四：思维拓展，即融合函数，形成探索三角形相似与函数问题的解题策略.

三角形相似模型微专题设计

关于“8字型”三角形相似模型微专题环节设计，结合上述分析可设计四个环节，各个环节中围绕教学重点设计探究内容，引导学生深刻理解模型，掌握模型应用方法. 环节设计中注意教学预设解读、问题引导设计.

教学环节一：模型归纳，知识解读

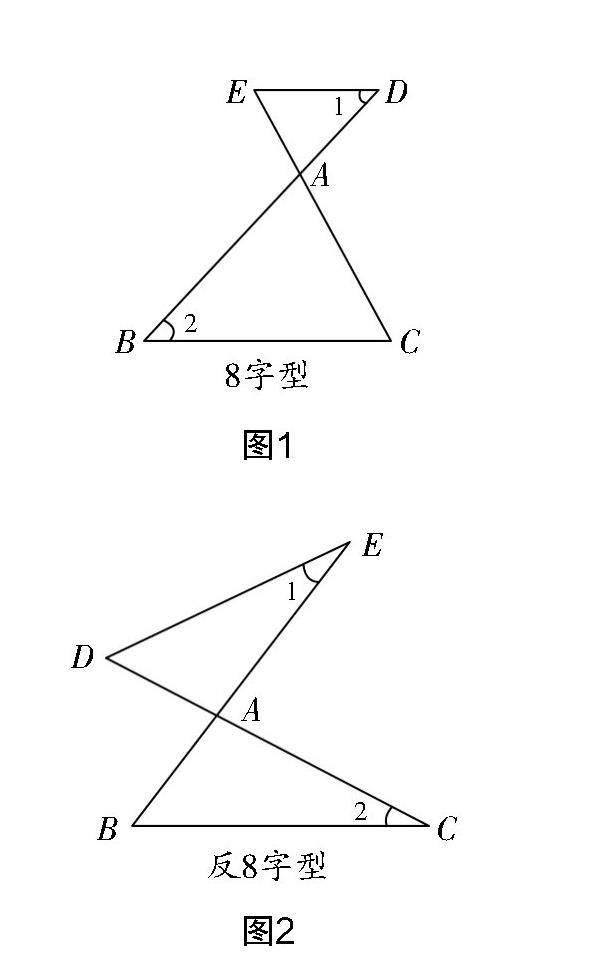
“8字型”三角形相似模型有两种情形，教学中呈现如图1和图2所示的模型，引导学生关注模型的特点，再探索其中的特性结论. 故可分为两步：第一步，特征分析；第二步，特性分析.

教学预设：教学中设计问题让学生关注模型的特征，分析模型结论.

问题1：上述是“8字型”三角形相似模型的两种情形，从外表看是否像“8字”？

问题2：分析模型的两种情形，观察其中ED和BC的位置关系，有何不同？

问题3：两个模型中均有∠1=∠2，是否可以证明△ABC∽△ADE？可以得出哪些结论？

教学引导：教学中引导学生关注特征，根据对应条件来构建模型，推导结论. 对于图1，若BC∥DE，则△ABC∽△ADE，可推导出==，为“8字型”模型. 对于图2，若∠1=∠2，则△ABC∽△ADE，可推导出==，则为“反8字型”模型.

教学建议：教学中要结合具体的模型，让学生直观分析，掌握模型的具体特征，并结合图形对比观察，深刻理解两大模型的相异点和相同点. 结论探究时注意逻辑性，从“条件”出发探索证明“模型”，再结合“模型”推导“结论”.

教学环节二：初步应用，思路分析

利用“8字型”三角形相似模型可以解决相关的几何问题，有利于解题思路的构建，该环节探究中首先设计一般性问题，注意解题过程的分析引导.

问题：如图3所示，在菱形ABCD中，EF⊥AC于点H，分别交AD于点E，CB的延长线于点F，且AE ∶ FB=1 ∶ 3. 则GB ∶ CD的值为______.

教学预设：上述为结构简单的一般性问题，以菱形为背景，求解线段比值. 解析引导时分为三步，第一步，引导学生理解图形的构建过程；第二步，引导学生分析条件，提取证明模型；第三步，结合模型结论进行推导，求解线段比值.

第一步，理解作图过程，提取条件信息. 结合菱形特性有AB=CD，AE∥BF；菱形ABCD中，EF⊥AC，F，B，C三点共线.

第二步，整合条件，提取模型. 分析图形，可推知∠EAB=∠ABF，∠AEF=∠F，从而可证明△EAG∽△FBG，即“8字型”三角形相似模型.

第三步，结合结论，推导求解. 由三角形相似可得==，可得=，所以=.

教学建议：模型应用初探阶段，需要注意引导学生整合图形条件，从中提取模型，再结合模型结论进行推理求解. 整个过程要注意严谨性和逻辑性，让学生理解解析过程中的关联，构建完成思维推理链.

教学环节三：深入探究，整合几何圆

将“8字型”三角形相似模型与圆相结合可以构建复合模型，在实际考查中也较为常见，以“反8字型”模型与圆结合为例，如图4所示，则有如下结论.

图4中，弦AC，BD交于点E，则△ABE∽△DCE，可推知=，整理可得AE·CE=BE·DE.

问题：如图5所示，正方形ABCD内接于☉O，点E为AB的中点，连接CE交BD于点F，延长CE交☉O于点G，连接BG.

（1）求证：FB2=FE·FG；

（2）若AB=6，求FB和EG的长.

教学预设：上述问题将“8字型”三角形相似模型与圆相结合，构建了复合模型，探究解析时注意结合圆的知识来探索提取模型，整个过程要注意整合条件，分析推理.

第（1）问中，把握三角形与圆的位置关系，推导条件：正方形ABCD内接于☉O，所以可推得AD=BC，则有∠ABD=∠CGB.

再结合∠EFB=∠BFG，则可以证明△BFE∽△GFB，完成模型提取.

后续利用模型求解：即三角形相似则有=，即FB2=FE·FG.

第（2）问中，首先整合处理其中的条件：点E为AB中点，则AE=BE=3. 由于四边形ABCD为正方形，则有CD=AB=AD=6，BD===6，CE==3.

再结合条件信息提取其中的特殊模型：因为CD∥BE，于是可证明△CDF∽△EBF，从而有====2.

后续整合条件信息求解：DF=2BF，CF=2EF，则有3BF=BD= 6，3EF=CE= 3，所以BF=2，EF= ，由（1）得FG===.

教学建议：在上述综合探究分析中，建议先构建三角形相似与圆相结合的模型，引导学生直观分析，再结合实例解读探索. 复合图形分析中，同样引导学生提取其中的相似三角形模型，结合结论推理分析.

教学环节四：思维拓展，融合函数

该环节需要对学生的思维进行拓展，形成相似三角形与函数的融合，构建具有“几何”与“函数”双重属性的复合型模型.

模型整合：如图6所示，抛物线中存在“8字型”三角形相似模型，即图中的阴影图形.

问题：如图6，P是直线BC下方抛物线上一点，连接OP交直线BC于点E，求的最大值.

教学预设：教学中首先引导学生关注其中的复合图形，然后在此基础上思考求解线段比值的思维方法. 整体思维过程如下.

第一步，过点P作PQ∥y轴交BC于点Q，则可以提取其中的“8字型”三角形相似模型，可得=.

第二步，由于OC为定值，所以的最大值就转化为求PQ的最大值问题.

第三步，结合条件利用坐标法求解最值即可，解析过程中要注意数形结合.

教学建议：“8字型”三角形相似模型与函数相结合在中考中十分常见，属于重难点问题，教学中建议按照上述过程解析模型，探索总结解题的基本思路，形成方法策略，再进行实例强化训练.

写在最后

相似三角形模型的探究教学中，教师可以参考上述微专题设计教学环节，引导学生整合教材的基础知识，构建特定模型，形成系统解题流程. 拓展探究中，教师可将其与圆、函数相结合形成复合模型，引导学生体验探究过程，强化解析思维，提升解题能力.

作者简介：周潇也（1996—），本科学历，中小学二级教师，从事初中数学教育教学工作.