基于区块链的视频流边缘计算卸载方案研究

马丽 李英

摘要：传统多媒体物联网难以满足对时延敏感和计算密集型视频处理任务的需求，且无法保证任务处理过程中的安全性和隐私性。为此，将移动边缘计算（Mobile Edge Computing，MEC）与视频流结合，提出一种基于区块链的MEC视频流网络架构（B-SMEC）。考虑斯塔克尔伯格动态博弈优化移动边缘服务器（Mobile Edge Servers，MES）、视频服务提供商（Video Service Providers，VSPs）和用户之间的视频资源分配，在满足用户动态视频服务请求的同时，实现MES与VSPs的效益最大化。应用区块链技术记录整个资源交易过程，保护其安全性和隐私性。仿真实验验证了该方案的有效性。

关键词：移动边缘计算；区块链；斯塔克尔伯格博弈；视频流；资源分配

中图分类号：

TP302.1

文献标志码：A

随着多媒体技术的不断发展，信息已经从简单的文字和图片发展到更复杂的音频和视频[1-2]。数字视频技术作为信息处理的一个重要分支，广泛应用在通信中。然而，许多视频流处理任务都是计算密集型且耗时较长，传统多媒体网络难以满足视频任务处理的需求[3]。为了解决算力不足、时延长的问题，移动边缘计算（Mobile Edge Computing，MEC）应运而生。MEC将计算和通信扩展到无线接入网络的边缘，并为用户设备提供边缘计算服务[4]。用户设备可以将计算任务转移到MEC服务器，通过无线蜂窝网络执行计算，然后卸载计算任务到单个或多个边缘设备[5-8]，以减少视频处理任务的延迟。计算应用程序的卸载率[9]，并通过边缘视频流系统节能优化框架[10]，使视频任务在卸载到边缘之前被压缩以节省带宽。区块链技术的分布式存储可以保障视频数据的可靠性和安全性[11]。基于MEC的转码框架[12]可以将区块链与视频流结合，利用智能合约促进非信任实体之间的分布式优化[13]。移动用户通过移动区块链网络的MECenabled框架[14]可以访问和利用边缘计算服务提供商的资源来支持他们应用区块链技术，区块链技术可以为视频流服务提供去中心化、版权保护、透明度和安全高效性等方面的帮助[15-16]。然而，传统区块链网络中PoW协议产生巨大的计算能耗，导致过度浪费计算资源[17]。为减少资源浪费，同时最优化效益问题，本文引入了一种PoS共识机制[17]并将移动边缘计算视频流服务与区块链相结合，构建基于区块链的MEC视频流网络架构（B-SMEC），利用斯塔克尔伯格博弈的方法讨论系统中MES、VSPs和移动用户之间的资源分配方案及各自的效应，在高效地使用MEC网络中计算资源的同时，保障了MEC网络的安全性和隐私性。

1 基于区块链的MEC网络架构

基于区块链的MEC网络架构结合了区块链技术和MEC技术，旨在提供更安全、可靠和去中心化的边缘计算环境。MEC通过在物理网络基础设施上部署计算和存储能力，使应用程序和服务更接近终端用户。这种边缘计算模型可以提供更低的延迟，减少网络拥塞，并支持更高效的数据处理。区块链以透明的方式保护数据和交易的准确性、一致性和有效性[18]。每个参与者都管理自己的密钥，数据和交易被加密并存储在块上，实现在没有任何第三方控制的环境下保护隐私和安全。区块链和MEC网络对计算卸载的集成旨在支持安全、分散和激励的边缘计算服务，以满足移动设备的计算需求[19]。

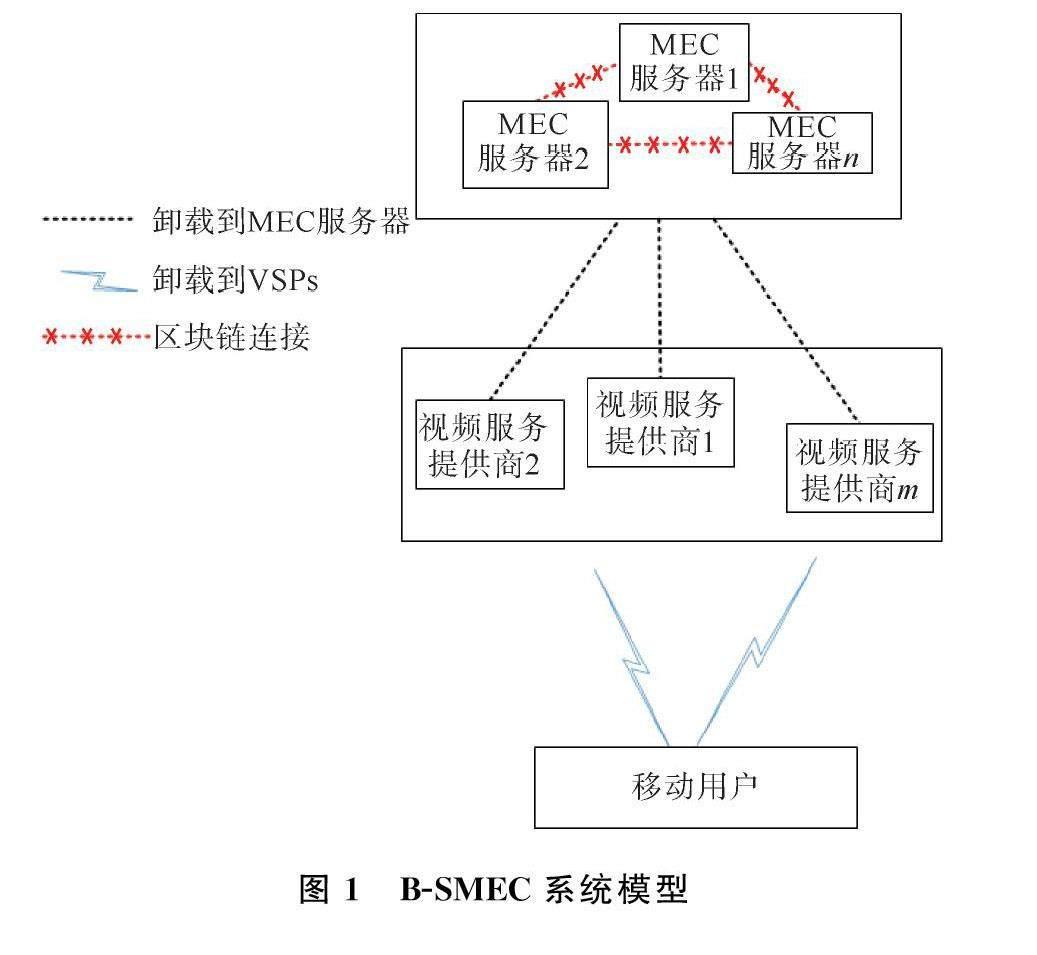
本文采用基于区块链的MEC视频流网络架构（B-SMEC），框架由多个移动边缘服务器（Mobile Edge Servers，MES）和视频服务提供商（Video Service Providers，VSPs）组成，分为：MES层、VSPs层和用户层（图1）。MES的集合由N表示，N=1，2…，N，VSPs的集合由M表示，M={1，2…，M}。在移动边缘服务器层中，有多个MES为VSPs分配边缘计算的视频资源，并假设MES中有足够的视频资源。VSPs为移动用户提供视频资源服务，因为VSPs视频资源的有限性，VSPs可以向MES请求边缘视频资源，以提高对移动用户的服务质量（QoS）。在用户层，每个移动用户将视频服务需求上传到VSPs。

为保证系统的安全性和隐私性，MEC系统模型集成区块链模块，系统中有4个角色：边缘计算视频资源请求者、边缘计算视频资源分配者、区块生成者和区块验证者。VSPs是边缘计算视频资源请求者，控制视频资源需求并从MES获得边缘计算视频资源；MES是边缘计算资源分配者，控制视频资源价格并将边缘计算视频资源分配给VSPs；MES还充当区块链系统中的区块生成者和区块验证者。在基于区块链的MEC系统中，控制资源价格和分配边缘计算视频资源后，MES充当区块链节点，将交易信息提交给区块链系统。

2 B-SMEC系统模型

2.1 用户服务请求模型

为了更好的描述用户的弹性服务需求和变化情况，使用Cobb-Douglas函数[20]定义用户的动态服务请求，可以更加直观、快捷的计算服务价格和传输速率对于用户服务需求的影响。由于参与用户服务的VSPs视频资源有限，VSPs会将一部分用户需求传输至MES进行计算。因此，用户的服务需求受服务价格和MES与VSP之间的传输速率影响。用户服务请求ui（t）为

ui（t）=φidi－1（t）pi（t）（1）

其中，pi（t）为t时第i（i∈M）个VSP向MES传输计算任务的传输功率，di（t）是VSP为用户提供服务的价格，φi为加权参数。

2.2 MES效益模型

MES与VSP之间通过无线信道进行传输，传输速率Ri（t）表示为[21]

Ri（t）=bilog2（1+pi（t）hiσ2i）（2）

其中，bi，hi，σi分别表示MES与VSPs之间无线信道的带宽、信道增益和高斯白噪声功率。

VSPs将计算任务上传至MES，MES完成计算任务并从中获得利润，在计算过程中产生计算能耗。ri（t）表示MES在t时提供给第i（i∈M）个VSP的计算资源的价格，ti表示MES与VSP之间无线传输时间。因此，得到MES需要处理的计算任务量Ri（t）ti。MES的服务效益由服务收益与计算耗损组成，服务效益UC（t）表示为

UC（t）=∑Mi=1ri（t）pi（t）－ρikci（fci）2 ∑Mi=1Ri（t）tiLi（3）

其中，ρi表示计算资源过程中的损耗系数，kci是MES自身的硬件能耗，fci是MES配备的处理器的计算频率，Li表示计算任务单位数据量所需要的计算负载。

作为区块链的节点，MES可以在区块链服务中获得奖励。MES是否被选为块生成者是由MES所拥有的“股份”决定，在基于PoS的共识协议中[22-23]，每个时隙利用“股份”制选举产生唯一的块生成者，这些“股份”由最新的资源服务收益度量。因此，在下一个时期选择MES服务器作为区块生产者的概率由其服务奖励与当前时期其他服务器的总服务奖励的比值决定，概率函数为

Pi（t）=ri（t）pi（t）∑Mj=1，j≠irj（t）pj（t）（4）

其中，ri（t）为最优资源价格。

MES作为区块链节点获得的收益表示为

UB（t）=RvPi（t）+Rg（1－Pi（t））（5）

其中，Rv表示MES为块生产者时生成的效益，Rg为块参与者时生成的效益。

MES的效益函数UMESi（t）由服务效益UC（t）和区块链奖励UB（t）两部分组成

UMESi（t）=UC（t）+UB（t）=∑Mi=1ri（t）pi（t）－ρikci（fci）2∑Mi=1Ri（t）tiLi+RvPi（t）+

Rg（1－Pi（t））（6）

2.3 VSP效益模型

收到用户请求时，VSPs使用自身资源及从MES处获得的资源为用户提供服务。每个VSP使用自身和边缘资源为用户提供需求服务。在t时刻，资源越多的VSP可以服务更多的用户。VSP通过向用户提供计算资源获得收入，t时第i（i∈M）个VSP的利润UVSPi（t）

UVSPi（t）=di（t）ui（t）－∑Mi=1γiri（t）pi（t）－μikui（fui）2（ui（t）－Ri（t）ti）Li（7）

VSP的收益包括三部分：di（t）ui（t）表示VSP向用户提供服务时获得的利润，ui（t）是用户的服务需求；γiri（t）pi（t）是VSP向MES请求资源时支付给MES的费用，γi是VSP支付成本的决策权重；μikui（fui）2（ui（t）－Ri（t）ti）Li表示VSP使用自身资源处理用户需求时的计算能耗，μi为平衡VSP的计算能耗和服务收益的权重，kui是VSP自身的硬件能耗，fui是VSP配备处理器的计算频率。

3 Stackelberg博弈框架

3.1 问题描述

在B-SMEC系统模型中，MES对资源价格ri（t）有决策权，需寻求合适的资源价格，以使利润最大化。MES的优化问题定义为

maxri（t） UiMES（t）

s.t.0≤ri（t）≤ri（t）（8）

VSP决定从MES请求资源的传输功率pi（t），以优化其利润，VSP的利润函数由式（7）给出，用户的动态资源请求由式（1）给出，VSP的优化问题可定义为

maxpi（t） UiVSP（t）

s.t.ui（t）=φidi－1（t）pi（t）  （9）

3.2 基于斯塔克尔伯格博弈的资源分配策略

本文采取Stackelberg动态博弈优化VSP的传输功率和MES计算资源的价格。作为领导者，MES首先向VSP宣布资源单价，VSP作为追随者将按照预期的边缘计算资源做出决策，计算资源需求上传到MES后，MES决定最佳价格以获得最大利润，此过程一直迭代到Stackelberg动态平衡。在Stackelberg动态均衡下，MES制定最优资源价格使利润最大化，同时，VSP达到最佳的资源传输功率使效用最大化。

定义1 对于MES，如果不等式（10）适用于所有价格ri（t）≠ri*（t），则资源价格ri*（t）是Stackelberg动态均衡

UiMES（ri*（t），pi*（t），t）≥UiMES（ri（t），pi*（t），t）（10）

定义2 对于VSP，如果不等式（11）适用于所有传输功率pi（t）≠pi*（t），则计算资源量pi*（t）是Stackelberg动态均衡

UiVSP（pi*（t），ri*（t），t）≥UiVSP（pi（t），ri*（t），t）（11）

3.2.1 VSP均衡博弈分析 VSP根据自身视频资源储备情况和资源价格决定卸载多少计算任务到MES，以有效地完成来自用户的计算任务并尽可能提高自身的收益。首先证明VSP具有唯一的最优卸载策略，并通过令效益函数的一阶导数为零求解该阶段的最优策略。

根据式（1），求得式（7）关于pi（t）的一阶导函数

UVSPi（t）pi（t）=φi－γiri（t）－μikui（fui）2Li（φidi（t）－bitihi（σ2i+pi（t）hi）ln2）（12）

得到二阶导函数

2UiVSP（t）pi2（t）=－μikui（fui）2Libitihi2（σ2i+pi（t）hi）2ln2（13）

可知，式（13）恒小于0，即VSP的效益函数是关于pi（t）的凸函数，因此pi（t）具有唯一最优策略。令式（12）等于0，求解最优的pi（t）

φi－γiri（t）－μikui（fui）2Li（φidi（t）－bitihi（σ2i+pi（t）hi）ln2）=0（14）

即

pi*（t）=μikui（fui）2Libiti（γiri（t）+μikui（fui）2Liφidi（t）－φi）ln2－σ2ihi（15）

为简化方便后续公式的表达，令Ri（t）=γiri（t）+μikui（fui）2Liφidi（t）－φi。

3.2.2 MES均衡博弈分析 为最大化MES效应函数，式（15）代入式（6），得MES的效用函数

UMESi（t）=（1+Rv－Rg∑Mj=1，j≠irj（t）pj（t））∑Mi=1ri（t）（μikui（fui）2LibitiRi（t）ln2－σ2ihi）+Rg－

ρikci（fci）2∑Mi=1bilog2（μikui（fui）2LibitihiRi（t）σ2iln2）tiLi（16）

计算式（16）关于ri（t）的一阶偏导数，得

UMESi（t）ri（t）=（1+Rv－Rg∑Mj=1，j≠irj（t）pj（t））∑Mi=1（μikui（fui）2LibitiRi（t）ln2－σ2ihi－ri（t）γiμikui（fui）2LibitiR2i（t）ln2）+

ρikci（fci）2∑Mi=1biγiLitiRi（t）ln2（17）

基于式（17），计算式（16）关于ri（t）的二阶导数

2UMESi（t）ri2（t）=－（1+Rv－Rg∑Mj=1，j≠irj（t）pj（t））∑Mi=12μikui（fui）2LibitiγiR3i（t）ln2（μikui（fui）2Liφidi（t）－φi）－ρikci（fci）2∑Mi=1biγi2LitiR2i（t）ln2（18）

定理1 当满足式（19）时，UMESi（t）为凸函数，MES的资源价格具有唯一的最优解

di（t）≤μikui（fui）2Li（19）

证明：针对式（18）中（γiri（t）+μikui（fui）2Liφidi（t）－φi）3和μikui（fui）2Liφidi（t）－φi，给出如下定义

f（t）=（γiri（t）+μikui（fui）2Liφidi（t）－φi）3

g（t）=μikui（fui）2Liφidi（t）－φi

当di（t）=μikui（fui）2Li时，f（t）=（γiri（t））3且g（t）=0，式（18）恒小于0；当di（t）<μikui（fui）2Li时，f（t）>0且g（t）>0，式（18）恒小于0。

现证明满足式（19）时，UMESi（t）为凸函数，MES的资源价格具有唯一的最优解，令式（17）=0，得

1+Rv－Rg∑Mj=1，j≠irj（t）pj（t）∑Mi=1μikui（fui）2LibitiRi（t）ln2－σ2ihi－ri（t）γiμikui（fui）2LibitiR2i（t）2ln2+

ρikci（fci）2∑Mi=1biγiLitiRi（t）ln2=0（20）

求解式（20）可以获得最优资源价格ri（t），然而式（20）中的ri（t）是一个非线性复杂的优化问题，用传统的数学方法很难求得最优解。为此本文设计了基于梯度上升的算法MISSM逼近ri（t）的最优解。首先，初始化一组随机的MES的单位资源价格ri（0）（t），并根据式（15）计算对应VSP的传输功率pi（0）（t）；然后根据式（2）以及pi（0）（t）计算每个MES的总负载，得到每个MES参与区块链生成的成功竞选概率及收益情况。通过梯度上升法，由式（20）对ri（t）进行迭代运算，得到ri（t）最终的收敛结果，即为最优单位资源价格ri*（t）。

4 数值模拟实验

通过模拟实验评估B-SMEC系统性能。

4.1 参数设置

考虑多个MES和多个VSP的视频服务系统模型，实验中使用了5个边缘计算服务器，每个服务器为2～20个VSP提供计算资源；MES的单位能耗为5 W；由于VSPs效率不同，能耗也不同，定为5～9 W，VSPs计算频率为1 ms；MES与VSP之间无线信道的带宽、信道增益和高斯白噪声功率分别设置为30 MHz、53 dBm、10 dB；计算任务的传输时间间隔为（0.5～2.5） ms。

4.2 结果分析

实验首先测试了不同区块链协议对系统效益的影响，如图2所示，相较于传统的PoW协议，PoS协议无论对MES还是VSP效益都有明显的增大。在PoS协议中，MES作为区块链的节点，参与区块链的存储服务，并从中获得一定的效益。VSP作为Stackelberg博弈的追随者，当MES的效益增加时，系统调整视频资源价格来实现双方效益的最大化。

使用MISSM算法计算系统的最优价格，从而实现MES和VSP的利润最大化目标。如图3所示，MES的资源价格随着迭代次数的增加逐渐接近其最优价格，MISSM算法可以快速地收敛到最优值，每个边缘计算服务器均可以找到最优单位资源价格。

由图4可知，当系统中参与用户服务的VSP数量过少时，为确保自身收益，MES会适当提高资源价格，因此，VSP的效益降低。而随着VSP数量的增加，系统中参与任务处理的单位越多，在用户请求足够的条件下，系统的任务处理效率增大，VSP效益也随之增加。且随着VSP设备单位负载能耗的增加，其对VSP效应的影响也变得更加明显。

图5中，传输时间越长，VSP将越多的计算任务卸载到MES上，从而增加MES的计算任务量，获得更高的收益。随着VSP服务价格的增大，VSP的效益函数也随之增加。Stackelberg动态博弈使任何一方效益增加的同时，另一方的效益也随之增加。

5 结论

本文基于斯塔克尔伯格博弈，分析了MES、VSP和用户之间的资源分配，获得博弈中领导者和追随者的最佳策略。通过数学推理，证明了MES与VSP之间的斯塔克尔伯格博弈具有唯一的斯塔克尔伯格均衡；将区块链网络同移动边缘计算相结合，保障了资源交易过程中的安全性和隐私性。模拟实验证明了基于区块链网络的移动边缘计算网络架构在提高计算资源利用率的同时有效地保障了整个网络的隐私性和安全性。

参考文献

[1]LEE M C， MOLISCH A F， SASTRY N， et al. Individual preference probability modeling and parameterization for video content in wireless caching networks[J].IEEE/ACM Transactions on Networking， 2019， 27（2）： 676-690.

[2]程茹秋， 余烨， 石岱宗， 等. 图像与视频质量评价综述[J]. 中国图象图形学报， 2022， 27（5）： 1410-1429.

[3]RAY D， KOSAIAN J， RASHMI K V， et al. Vantage： Optimizing video upload for time-shifted viewing of social live streams[C]// ACM Special Interest Group on Data Communication. Beijing， 2019： 380-393.

[4]ABBAS N， ZHANG Y， TAHERKORDI A， et al. Mobile edge computing： A survey[J]. IEEE Internet of Things Journal， 2017， 5（1）： 450-465.

[5]CHEN L X， GONG G Q， JIANG K， et al. DDPG-based computation offloading and service caching in mobile edge computing[C]// IEEE Conference on Computer Communications （INFOCOM WKSHPS）.Electr Network， 2022： 1-6.

[6]张斐斐， 葛季栋， 李忠金， 等. 边缘计算中协作计算卸载与动态任务调度[J]. 软件学报， 2023， 34（12）： 5737-5756.

[7]LIANG Y T， HE Y J， ZHONG XX. Decentralized computation offloading and resource allocation in mec by deep reinforcement learning[C]// IEEE/CIC International Conference on Communications in China （ICCC）. Electr Network， 2020： 244-249.

[8]WANG Y T， SHENG M， WANG X J， et al. Mobile-edge computing： Partial computation offloading using dynamic voltage scaling[J]. IEEE Transactions on Communications， 2016， 64（10）： 4268-4282.

[9]CHEN N， ZHANG S， QIAN ZZ， et al. When learning joins edge： Real-time proportional computation offloading via deep reinforcement learning[C]// 25th International Conference on Parallel and Distributed Systems （ICPADS）. Tianjin， 2019： 414-421.

[10] LIU M T， YU F R， TENG Y L， et al. Computation offloading and content caching in wirelessblockchain networks with mobile edge computing[J]. IEEE Transactions on Vehicular Technology， 2018， 67（11）： 11008-11021.

[11] SARASWAT D， VERMA A， BHATTACHARYA P， et al.Blockchain-based federated learning in UAVs beyond 5G networks： A solution taxonomy and future directions[J]. IEEE Access， 2022， 10： 33154-33182.

[12] LIU M T， YU F R， TENG Y L， et al. Distributed resource allocation inblockchain-based video streaming systems with mobile edge computing[J]. IEEE Transactions on Wireless Communications， 2018， 18（1）： 695-708.

[13] LIU M T， TENG Y L， YU F R， et al. A mobile edge computing （MEC）-enabled transcoding framework forblockchain-based video streaming[J]. IEEE Wireless Communications， 2020， 27（2）： 81-87.

[14] XIONG Z H， ZHANG Y， NIYATO D， et al. When mobileblockchain meets edge computing[J]. IEEE Communications Magazine， 2018， 56（8）： 33-39.

[15] QIU C， YAO H P， JIANG C X， et al. Cloud computing assistedblockchain-enabled internet of things[J]. IEEE Transactions on Cloud Computing， 2022， 10（1）： 247-257.

[16] KOTOBI K， BILEN S G. Secureblockchains for dynamic spectrum access： A decentralized database in moving cognitive radio networks enhances security and user access[J]. IEEE Vehicular Technology Magazine， 2018， 13（1）： 32-39.

[17] OUYANG Z Q， SHAO J， ZENG Y F.PoW and PoS and related applications[C]// International Conference on Electronic Information Engineering and Computer Science （EIECS）. Changchun， 2021： 59-62.

[18] TAN Z， YU F R， LI X， et al. Virtual resource allocation for heterogeneous services in full duplex-enabled SCNs with mobile edge computing and caching[J]. IEEE Transactions on Vehicular Technology， 2017， 67（2）： 1794-1808.

[19] LENG J W， ZHOU M， ZHAO J L， et al.Blockchain security： A survey of techniques and research directions[J]. IEEE Transactions on Services Computing， 2022， 15（4）： 2490-2510.

[20] TAGHAVI M， BENTAHAR J， OTROK H， et al.Cloudchain： A blockchain-based coopetition differential game model for cloud computing[C]// 16th International Conference on Service-Oriented Computing （ICSOC）. Hangzhou， 2018： 146-161.

[21] 赵竑宇. 资源受限的移动边缘计算系统中计算卸载问题研究[D]. 北京： 北京邮电大学， 2019.

[22] KIAYIAS A， RUSSELL A， DAVID B， et al.Ouroboros： A provably secure proof-of-stake blockchain protocol[C]// 37th Annual International Cryptology Conference （AICC）. Santa Barbara， 2017： 357-388.

[23] GAZI P， KIAYIAS A， ZINDROS D. Proof-of-stake sidechains[C]// IEEE Symposium on Security and Privacy （SSP）. San Francisco， 2019： 139-156.

Research on Blockchain-based Edge Computing Offloading

Scheme for Video Streaming

MA Li， LI Ying

（School of Computer Science and Technology，Qingdao University，Qingdao 266071，China）

Abstract：

Traditional multimedia IoT is difficult to meet the demand for delay-sensitive and computationally intensive video processing tasks， and cannot guarantee the security and privacy during task processing. For this reason， a blockchain-based MEC video streaming network architecture （B-SMEC） was proposed by combining Mobile Edge Computing （MEC） with video streaming. Based on the Stackelberg dynamic game to optimize the video resource allocation among mobile edge servers （MES）， video service providers （VSPs） and users， the benefits of MES and VSPs were maximized while satisfying users' dynamic video service requests. Blockchain technology was applied to record the whole resource transaction process to protect its security and privacy. The effectiveness of the proposed scheme is verified through simulation experiments.

Keywords：

mobile edge computing; blockchain; Stackelberg game; video streaming; resource allocation