求联求通：让儿童看到“水”、想到“鱼”

数学教育的本质在于培养学生的思维，即会想问题。然而，现实的数学课堂教学中还存在零散性地教、碎片化地学的现象，学生的数学眼光和思维也只是“看山是山、看水是水”的低水平状况。那么如何让学生透过数学的“水面”，想到深层的“鱼”，发展学生的数学思维呢？“求联求通，整体建构”不失为一种好的学习方式。

“求联求通”是指把数学中具有内在联系的不同领域的内容或问题有机地统整在一起，加强纵向和横向的配合，构成具有整体性的课程结构。主要体现在三个方面：第一个是联系，联系强调的是关联而不是孤立；第二个是通透，通透强调的是建构而不是复制；第三个是迁移，迁移强调的是运用而不是记忆。在课堂教学中又该如何实施呢？

一、前后关联：内容“串”起来，想得更全

数学是一门逻辑性、系统性很强的学科。数学的内容本身就是一个整体，它是由若干知识建构起来的具有严密逻辑联系的数学知识结构系统。因此，在教学中教师要树立整体意识，站在全局的视角，适时帮助学生“回头看”和“向前看”，把教学内容串起来，打通前后联系。

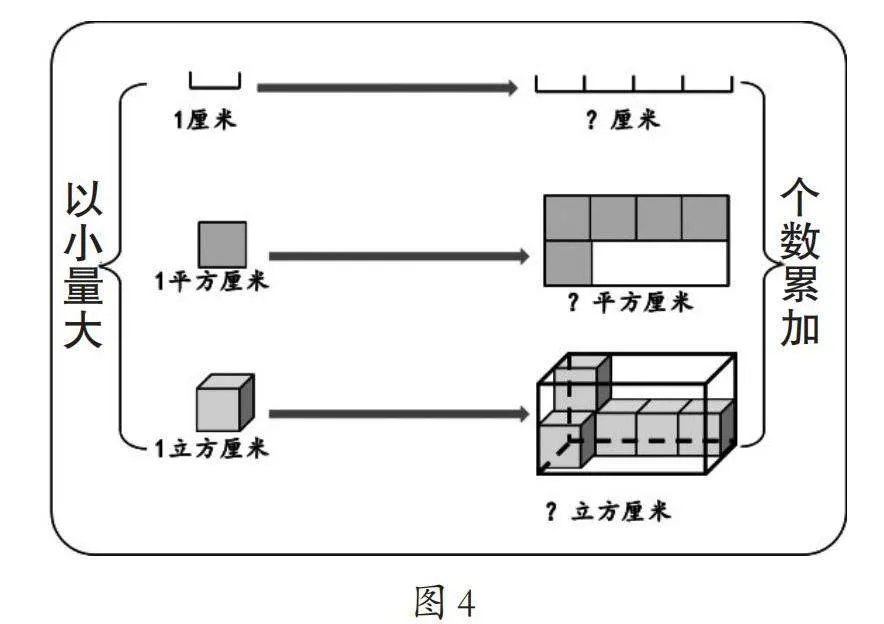
例如，在教学“分数乘整数”时，学生得出“分母不变，分子与整数相乘，积做分子”的算法后，教师适时来个“回马枪”，引导学生回顾整数、小数乘法，帮助学生理解算理。在学生思考交流后，教师用一组算式“40×30，0.4×0.3，[4/11]×3”引导学生思考，从中学生发现看似不同类的数相乘，它们的计算方法却有相同之处。其实面对每个算式学生心里都在算4×3＝12，教师再次追问：为什么你心里算的都是4×3=12，结果却不同？奥秘在哪儿？学生思考后发现其中的不同就是因为计数单位不同。（如图1）这样不仅让学生掌握了“分数乘整数”的计算方法，还明白了在“分数乘整数”运算过程中，为什么分母不变的道理。继而教师引导学生“向前看”，并猜想分数乘分数该怎么算，顺利沟通了知识间的联系：不论是整数乘法、小数乘法，还是分数乘法，其实质都是“个数乘个数得到了新个数，计数单位乘计数单位得到了新的计数单位”。

二、内外互联：概念“联”起来，想得更透

数学概念是数学的基石，理解概念离不开表征。表征作为认知心理学的一个重要概念，在数学教育中主要指学生在面对新概念时心理活动的表现和记录的方式，它既是认知活动的过程，又是认知活动的结果。教学中，常常需要通过外部的多元表征来解释数学内部的核心概念：一是采用“联”想开花，即多元表征核心概念；二是采用“联”想接龙，即链接概念与概念，学生看到此概念想到彼概念，这样学生在“联”中对概念的本质会想得更通透。

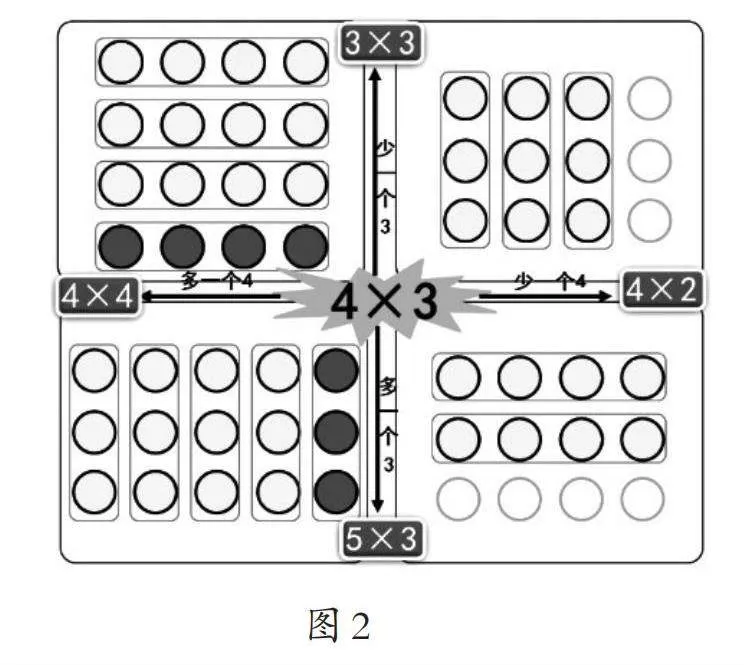
例如，在教学“乘法初步认识”时，在探究环节，笔者一方面通过多元表征策略让学生表达对“4×3”含义的理解。课堂上学生充分地自主表达、尽情地思维碰撞，诠释了他们个性化的解读。有的学生想到了用摆圆片、排正方体、画线段图等方式诠释“3个4”，将形的直观和数的抽象有效连接。有的学生想到了用“讲故事”的方式进行解读，如：每本日记本3元，4本多少元？每个文具盒4元，3个多少元？等等，学生将数学算式与生活应用建立了关联。还有的学生把4×3与3×4以及4＋4＋4和3＋3＋3＋3进行算式与算式之间的关联。多元表征，促使形、式、应用有机结合。另一方面借助变式和图示进一步打通算式与算式之间的关系，学生由“4×3”的含义，联想到：“多一个4”和“少一个4”分别怎样表示？他们想到了算式“4×2”“4×5”，进一步又联想到“2×3”“5×3”，联想接龙沟通了“4×3”与“4×2”“4×5”以及“2×3”“5×3”之间的关系，借助图示表征打通了算式之间的关联，学生深刻理解了乘法概念的内核。（如图2）

三、古今贯通：文化“融”起来，想得更清

2022年版课标指出：数学承载着思想和文化，是人类文明的重要组成部分。各种版本的教材都适时地介绍了相关的数学文化背景知识，这些知识既包含了数学在自然与社会中的应用，也包括数学的发生、发展脉络。教学中不可只将其作为点缀和调料，而应适时地将数学文化融入课堂，发挥其人文价值、审美价值和应用价值，学生自然会以古思今、由今想古，数学思维在古今对照中穿梭前行、融会贯通，进而更好地认识数学、理解数学、应用数学。

比如，在教学“三角形面积”时，学生在用两个完全一样的三角形拼成平行四边形得出其面积后，笔者并没有就此罢休，而是引导学生反思：“回顾研究平行四边形面积的经验，沿着高剪开转化为学过的图形，用这种方法研究三角形面积似乎不好用了，你们有什么启发？”一石激起千层浪，学生在深入思考后，探究出多种推导三角形面积的方法：有的沿其高剪开，想象出两个小长方形，进而推出三角形面积为大长方形面积的一半；有的沿中位线剪开转化为一个平行四边形；还有的沿中位线两端点向底边作高再转化为长方形（如图3）……教师顺势出示《九章算术》中的“圭田术曰，半广以乘正从”，让学生进行解释……整个过程，学生古今相连、由此及彼，思路逐渐深入清晰，分与合的思想，出入相补、以盈补虚的方法都慢慢地根植于学生内心。

四、远近互通：经验“立”起来，想得更远

数学基本活动经验和数学基本思想是“新双基”，它是学生素养形成的关键。类比思想就是根据数学知识之间的相同或相似的因素，从学生已有经验探索发现未知，抽丝剥茧般地解决数学问题的一种思维方式。它能够引领学生从整体上系统深入地掌握数学知识、领悟数学思想，而学生的数学活动经验是打通新旧知识的关键纽带。因此在教学中，我们要激发学生经验、利用学生经验、迁移学生经验，让经验“立”起来，促进学生形成触类旁通、举一反三的思考力。

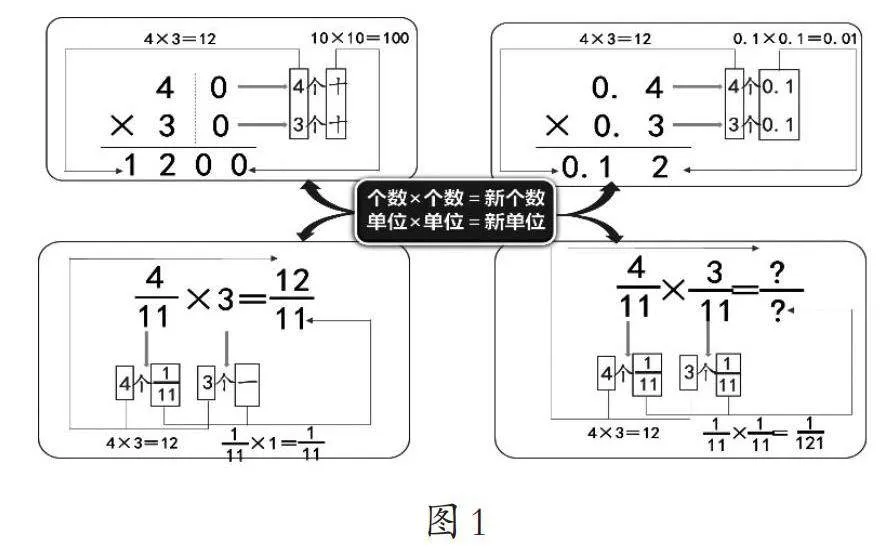
比如，在教学“体积与体积单位”时，让学生比较两个长方体盒子的大小，教师引导学生回顾以前比较线段长短、面积大小的活动经验……由此，学生想到了要用更小的正方体作为比较的标准，然后填满长方体再进行比较（如图4）……在思辨和探索中“以小量大、个数累加”的度量思想和经验贯通了图形测量的整个世界。

“求联求通，整体建构”需要根据教学内容的不同而灵活运用、联通有无，借助内容的前后联系、知识的多元表征、思想的古今贯通和经验的迁移类比等实现纵向打通和横向关联，从而实现数学点、线、面（也就是元素、关系到结构）的整体建构。学生的思维也能自主地联得起线、织得成网、明得出理、悟得出道……在“求联求通”中学生学会数学地思考，想得更清晰、更深入、更全面、更合理，学生的数学素养自然生成……

（作者单位：山东临沂市罗庄区沂堂镇中心小学）