怎样借助点子图帮助学生更好地理解四边形的概念

在学习四边形的认识时，借助点子图能帮助学生更好地理解四边形的概念，具体可以这样做：

一、画任意四边形

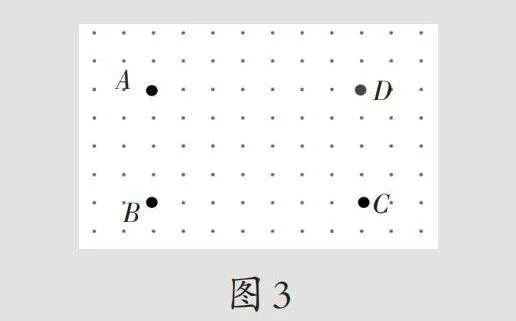
出示点子图和已知三点，（如图1）要求：根据已知的三个点A、B、C，再找一个点D，围成任意四边形。

教师收集并展示若干学生的作品（点D均在三角形ABC的外部，围成凸四边形），引导学生思考是否还有其他符合条件的点D，然后与同桌按“找点D—想形状—画验证”的步骤进行互动。

教师提问：“我们在三角形ABC的外部找了很多个点D，还有别的想法吗？”根据学生回答，教师出示在三角形ABC内部的点D。继续引导学生想象四边形的形状并思考形状是否唯一。

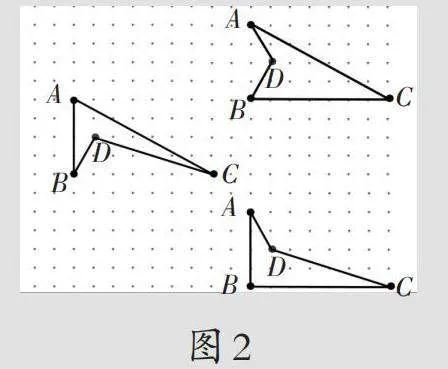
得出结论：无论点D在三角形ABC的外部还是内部，都能围成四边形。若点D在三角形ABC的内部，（如图2）则围成凹四边形且形状不唯一。我们一般说的四边形是指点D在三角形ABC外这种情况。

二、画长方形

出示学生找到的特殊点D。（如图3）想象：还是四边形吗？

有的学生认为该四边形是长方形，因为有四条“直边”且对边相等。教师追问：如何知道对边相等呢？学生借助点子图，通过数出对边的长度进行验证。教师质疑：仅满足对边相等就是长方形吗？学生补充条件：还必须有四个直角。学生进一步借助点子图验证有四个直角。

得出结论：判断一个四边形是不是长方形，需要结合边和角的特征。

三、画平行四边形

出示点子图和已知三点，（如图1）要求：根据已知的三个点A、B、C，找一个点D，围成平行四边形。

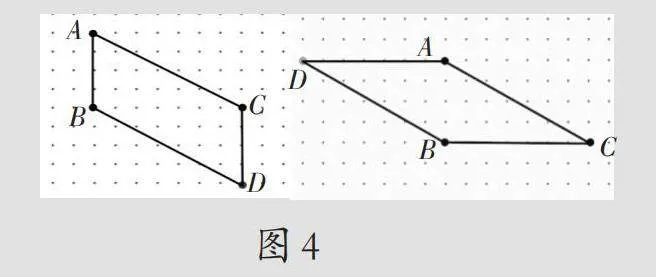
引导学生初步感知平行四边形对边相等且平行，并根据图4得出：对边除了与线段AB相等，还可与线段BC相等。

教师提问：我们在点子图上找到不同的点围成各种四边形，是否存在不能围成四边形的点？学生进行全面、有序的思考后明白：如果点D在直线AB、AC、BC上，就不能围成四边形。

教师追问：到底怎样的四个点才可以围成四边形？学生讨论，得出结论：同一平面内的四点，只要三个点不在同一条直线上，就可以围成四边形。

（作者单位：浙江乐清市育英寄宿学校）