明算理、通算法，感悟运算的一致性

分数计算是小学数学中数的计算的最高阶段，而“同分母分数加、减法”正是这个阶段的起始内容。学生在三年级学习“分数的初步认识”时已接触过“同分母分数加、减法”，并积累了借助几何直观说明算理的经验。人教版教材五年级下册“分数的加法和减法”这一单元的起始课再次安排学习“同分母分数加、减法”，其作用与价值何在？带着这样的思考我们对这节课进行了多次研讨。

2022年版课标指出：小学阶段在感悟数的概念本质上的一致性的基础上，还要感悟数的运算以及运算之间的关系，体会数的运算本质上的一致性，形成运算能力和推理意识。由此，再次教学“同分母分数加、减法”时，我们把教学的着力点放在：1.理解加、减法意义的一致性和“分母不变，只把分子相加、减”的道理；2.沟通分数、整数及小数加、减法之间的联系，感悟计数单位在运算中的作用，体会数的运算本质上的一致性，以达到培养运算能力和推理意识等素养的目标，为后续学习分数计算奠定基础。教学片段如下：

片段一：关联旧知，理解加、减法意义的一致性

师：大家对这个课题熟悉吗？同分母分数加、减法如何计算，在三年级上学期就学过，为什么还要学呢？今天再次学习同分母分数加减法，要进一步研究它的意义以及计算法则。

（教师出示主题图，如图1，并让学生提出问题）

生：爸爸和妈妈一共吃了多少张饼？

生：爸爸比妈妈多吃了多少张饼？

生：还剩多少张饼？

师：怎样列式计算呢？为什么这样列式？

生：要求爸爸和妈妈一共吃了多少张饼，就是把爸爸吃的和妈妈吃的两部分饼合起来，用加法计算，列式为[3/8]+[1/8]=[4/8]。

生：要求爸爸比妈妈多吃了多少张饼，就从爸爸吃的饼里面去掉和妈妈吃的同样多的部分，用减法计算，列式为[3/8]-[1/8]=[2/8]。

师：要求还剩多少张饼，怎么列式？

生：从整个饼里减去爸爸吃的和妈妈吃的，就是1-[3/8]-[1/8]=[4/8]。

师：看来，同学们运用原来的知识和经验，知道把两个数合起来，用加法计算，求一个数比另一个数多多少用减法计算。而这些数不管是整数、小数还是分数，其加、减法的意义都是一样的。

（教师出示课件，如图2）

师：现在谁能分别说说分数加、减法的含义？（生答略）

【思考】开课点题，激活学生已有的知识和经验，明确学习任务，学有方向。再创设熟悉的问题情境，放手让学生自主解决分数加减法的实际问题，结合具体情境理解分数加减法的意义，同时关联旧知，理解整数、小数、分数加减法意义的一致性。

片段二：借助直观，感受同分母分数加法数与形算理的一致性

根据课前诊断，了解到学生知道“同分母分数加、减法，只把分子相加、减，分母不变”这一算法，但对于“分子相加、减，计算的是什么？分母为什么不变”的道理解释不清。针对学生的认知障碍，我们把理解同分母分数加、减法的算理作为教学的重点、难点加以突出和突破。

师：为什么同分母分数加法可以把两个分数的分子直接相加，而分母却不用相加呢？（学生欲言又止）为了理解这个问题，请大家完成学习单，如图3。

（教师收集有代表性的学生作品，然后展示分享）

生1：我把一个圆平均分成8份，取其中的1份涂上红色表示[1/8]，再取其中的3份涂上蓝色表示[3/8]，涂色部分合在一起共占了这个圆的4份，就是[4/8]，所以是[3/8]+[1/8]=[4/8]。

生2：我是把一个长方形经过3次对折，其中的1份也就是这个长方形的[1/8]，先用红色将其中的3份涂色，再用黄色涂出其中的1份，这样涂色部分就有4份，共占了这个长方形的[4/8]，说明[3/8]+[1/8]=[4/8]。

生3：我的想法是，先画一条线段，把它平均分成8份，用一个括号标出其中的3份表示[3/8]，再用一个括号标出其中的1份表示[1/8]，3份加1份正好是4份，也就是这条线段的[4/8]，说明[3/8]+[1/8]=[4/8]。

生4：以上三位同学都选择了画图的方法，我觉得不用画图也能说明白。[3/8]和[1/8]两个分数的分母都是8，它们的分数单位都是[1/8]。[3/8]就是3个[1/8]，[1/8]就是1个[1/8]，加起来就是4个[1/8]，也就是[4/8]。

师：你们明白生4的思路吗？说说看。

（教师借助课件引导学生说理，强化3个[1/8]加1个[1/8]，是4个[1/8]，就是[4/8]，如图4）

师：怎样把你们的思考过程在算式中表示出来呢？

（学生独立思考，完成[3/8]+[1/8]= =[4/8]，教师指着学生填写的[3+18]追问）

师：这里的分母8不变表示的是什么？分子3+1表示的是什么？

生：分母8不变是分数单位没有变，3个[1/8]加1个[1/8]，结果是4个[1/8]，分母还是8。

生：分子3+1表示的是分数单位的个数相加，得到4个[1/8]，就是[4/8]，还可以化简成[1/2]。

师：你很会思考，能灵活运用刚学的约分，把计算结果中的分数化成最简分数。通过以上的学习，你们觉得同分母分数加法的算法是什么？

生：我发现同分母分数的加法很简单，就是分母不变，只把分子相加，计算结果能约分时，约分成最简分数。

师：现在能解释为什么分母不变吗？只把分子相加，加的是什么？

生：因为相加时分数单位不变，所以分母不变；分子相加，加的是分数单位的个数。

师：解释得好！同分母分数相加时，分母相同也就是计数单位相同，所以分子可以直接相加。这也是为什么同分母分数加法中分母不变的原因。

【思考】抓住学生认知的盲点，以“源头”问题激发学生通过独立思考、动手操作、合作交流等学习方式，借助直观图形、数分数单位的个数等方法解释说明同分母分数加法的算理。教师利用课件直观展示多种方法之间的联系，引导学生在感受数与形算理的一致性的基础上，以理驭法，强化对同分母分数加法的算理、算法的理解，有效突破难点。

片段三：沟通联系，感悟加、减法运算的一致性

师：通过探究大家发现，在同分母分数加法中，分母不变、分子相加是因为它们的分数单位相同，直接把分数单位的个数相加。那整数和小数的加法是怎样相加的？对比下面的一组算式，你们有什么发现？先独立思考，再与小组成员交流想法。

课件出示：

[3/8]+[1/8]=[4/8]

30+10=40

0.3+0.1=0.4

（学生组内交流后，集体分享）

师：哪个小组愿意分享你们的想法？

生：我们认为这三个算式都在计算3+1=4。

生：第一个算式是计算3个[1/8]加1个[1/8]，等于4个[1/8]；第二个算式是计算3个十加1个十，等于4个十；第三个算式是计算3个0.1加1个0.1，等于4个0.1。

师：也就是说，三个算式我们只计算了3+1=4。那在计算过程中变化的是什么，不变的又是什么？

NvN9UcjI3w6Bh5i+L0sBCA==生：变化的是计数单位，不变的是算式3+1=4。

师：同一个算式3+1=4，计算的是什么？

生：是不同计数单位的个数。

师：好，一语道破天机！想一想，为什么在初学整数加法时老师要提醒大家把相同数位对齐，在计算小数加法时把小数点对齐呢？

生：因为计数单位相同，才可以相加。计算时相同数位对齐是为了把相同的计数单位的个数相加。

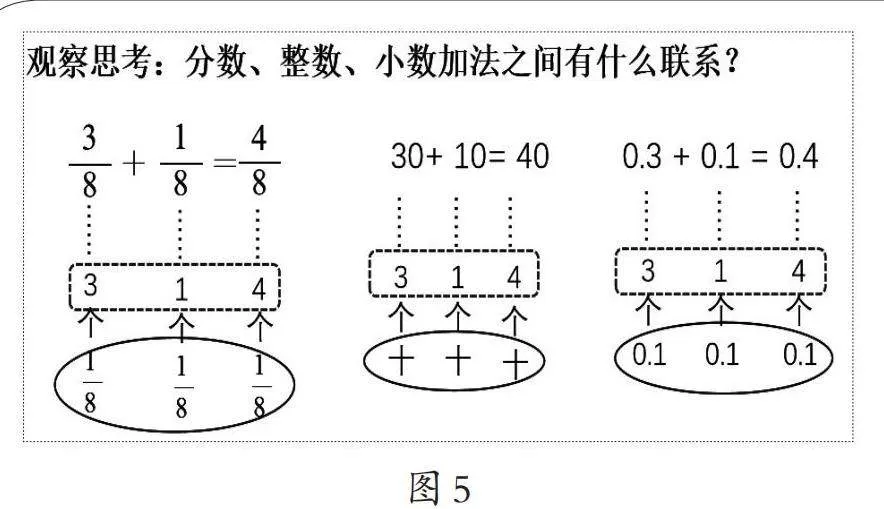
师：同学们很善于观察和思考，在分数、小数及整数的加法中，虽然计数单位不同，但在进行计算时，都是相同计数单位的个数累加。在整数、小数加法中，表现为相同数位对齐、小数点对齐，而在同分母分数加法中，表现为分母不变。（课件出示图5）

师：无论是整数、小数还是分数，在加法计算的过程中都是把相同计数单位的个数进行累加，其算理是相通的。同样的道理，在减法计算的过程中都是把相同计数单位的个数相减。下面请用刚才的学习方法独立解决第二个问题：解释说理[3/8]-[1/8]=[2/8]。

（学生运用类比的方法，自主完成同分母分数减法计算过程的书写及说理，集体交流，理解“同分母分数相减，分母不变，只把分子相减”的道理，概括出同分母分数加、减法的计算法则，并用字母式表示）

【思考】通过一组三个算式的比较，帮助学生把小学阶段数的计算构建成统一体系，初步感知数的运算实际上就是相同计数单位个数的运算的道理，感悟加、减法运算的一致性。同时，让学生从同分母分数加法类比到同分母分数减法的计算与说理，概括计算法则，用字母式表示，经历由特殊到一般的过程，培养学生的推理意识、符号意识及运算能力等数学素养。

（作者单位：湖北襄阳市襄州区教育教学研究中心）