小学数学教材中估计内容的编排分析

估计在日常生活中运用广泛。在21世纪初的课程改革中，估计被纳入小学数学课程的范畴。2022年版课标进一步强调估计的重要性，如“能在简单的真实情境中进行合理估算，作出合理判断”“初步感知度量工具和方法引起的误差，能合理得到或估计度量的结果”。本文拟从2022年版课标的角度，审视小学数学教材中估计内容的编排。

一、估计的类型

估计是指不经过物理操作而迅速给数学问题提供一个近似答案的心理操作过程，主要包括三种类型：测量估计（简称估测）、数量估计（简称估数）和计算估计（简称估算）。估测是指在不使用一般的测量工具的情况下，用某种方法推测出测量结果的一种心理加工过程，是一种实用的日常数学技能，主要包括对长度、面积、质量、温度等日常数学范畴的估计。估数是指在没有足够时间数出物体的数量，或要数的物体数量过大，或对非静止的物体根本无法做出计数的情况下，做出的一种粗略估计，是一种高层次的认知加工过程。除了对物体的数量进行估计，对数的运算结果的估计也属于数量估计。估算是指通过对原始数的近似值进行一些心理计算从而找到计算结果的估计值。

二、现行教材中估计内容的分析

对现行北师大版教材、人教版教材和苏教版教材中估数类、估测类和估算类习题的数量进行统计，发现三个版本教材中估算类习题最多，估测类习题最少。2022年版课标提高了对估测能力的要求，以培养学生的量感，所以应考虑增加估测类习题。

（一）估测类习题。

三个版本教材中的估测内容主要是对各种单位的感知及估测的方法，一般按照“长度—面积—体积”这条线进行编排，具有连贯性，其中穿插了时间、质量和角度的估测。

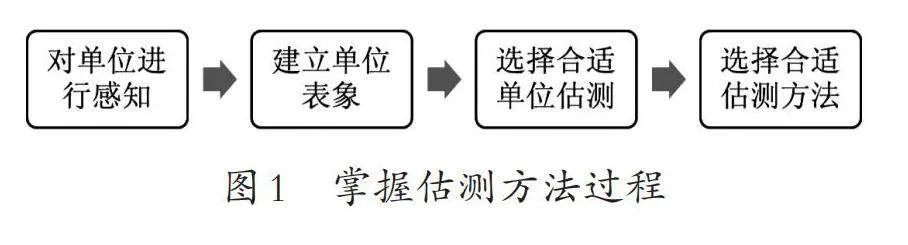
小学阶段常用的估测方法有单位迭代、参照点和在估计前对估计物进行心理转换。2022年版课标的要求是先会选择合适的单位估测，再选择合适的方法估测。学生要获得这种能力，应遵循图1所示的方式。教材在认识单位的课程内容中只是用图片帮助学生建立对单位的感知和认识，且物体的属性与现实生活不相符，而对单位的感知需要学生通过参加更多的实践活动来实现，也就是在“综合与实践”领域内加强对单位量的感知形成量感并不断运用。教材可以结合习题适当点明估测方法，用通俗易懂的语言进行描述，例如，参照点是指用一个我们已经知道长度或面积的物体测量另一个物体。

关于“先估计，再测量”，苏教版教材中的题目是先让学生估计，再进行测量，而北师大版教材中的题目往往追加一个问题（如图2）“估计时你有什么好办法”，意在了解学生是否真正掌握了估测的方法和策略。

要考查估测，提问方式很重要。例如，人教版教材中的这道题（如图3）。它要求学生比较所要估测的物体长度与给定长度的关系，这种方式贴近生活。有时我们只需要判断出一个长度比一个常用数量级单位长还是短，或判断出一个物体的长度大概属于哪个数量级即可。例如，TIMSS（国际数学与科学趋势研究）中对于估测是这样考查的：估计此铅笔（图略，原图中铅笔的长度为13厘米）的长度约是多少。（四个选项分别是5厘米、10厘米、20厘米、30厘米）

（二）估数类习题。

估数类习题的主要类型为：写出某个接近整十、整百或整千的数（类型1），利用“四舍五入”法直接写数的近似数（类型2），对计算的结果进行近似估计（类型3）。三种类型呈现难度递进上升的趋势。

各版本教材一般都是在四年级上册介绍“四舍五入”法，其中人教版教材和苏教版教材在学习万以内的数时就介绍了近似数或约等号，并出现“写出整十、整百、整千的数”这类题目，这其实是为后面介绍“四舍五入”法进行铺垫，相当于一个过渡阶段，符合教材编写螺旋上升的要求。

类型3的习题，是为了帮助我们更快地判断一个数量是否符合要求。如此一来，当计算出结果后，对于如何判断结果是否在某个范围内，应有相应的教学，否则形同虚设。

此外，“四舍五入”法不仅在自然数中适用，在小数中也适用，并且生活中经常出现把万以上的数改写成以万为单位或以亿为单位的数这类问题，它们的解决需要用到“四舍五入”法。从这一角度看，求小数的近似数的习题是有必要的。

（三）估算类习题。

陈丽兰等把估算策略大概分为：数字转换策略和结果调整策略。数字转换策略即对数进行一些处理，结果调整策略是对估算出的结果进行调整使其更接近精确值[1]，教材中主要体现的是第一种策略。因此，估算类习题的主要类型为：纯数字估算（类型1），实际应用背景下的估算（类型2）。

对于纯数字估算，有研究发现估算能力与精算能力均会参与个体计算过程，并且随着问题的改变，两类区域的激活程度均会发生相应的改变[2]，因此估算和精算是无法做到精准分离的。曹一鸣教授认为，估算放在计算后通常具有检验的功能，放在计算前通常具有预测的功能。教师要引导学生体会这两个功能，教材中出现的“先估计，再计算”或“先计算，再估计”习题，本意也是想突出这两个功能。但是，实际练习中，对于“先估计，再计算”这类题，大部分学生往往跳过估计部分而直接进行精确计算。为达成估计教学的目的，不妨稍做改动：只要求学生估计，要求学生在短时间内估计出结果，并写下估计过程。考虑到对于同一道题可以采用不同的估算策略，因此，估计的结果不唯一，只要是合理的就可以。

再如，除法的估算习题里面，三个版本教材基本都要求学生用估算试商，并且很多题目仅仅是“先判断商是几位数，再进行计算”。在实际练习这些题目时，也会出现学生只进行精算的现象。在这个问题的解决上，人教版教材和北师大版教材设计的估算类题（如图4和图5）是值得借鉴的。

同样，针对学生在完成“先计算，再估计”这类题时得到精确结果后不再进行估算的情况，题目设计也可以略作改动。比如，直接给出一个错误的计算结果，并且是一个比较复杂的式子，让学生通过估算判断结果是否正确，这样不仅让学生放弃通过直接计算来判断，而且让学生意识到估算有时比精算更方便。

在实际应用背景下的估算内容，一部分是含有明显估计特征词的显性估算题，另一部分是没有明显估计特征词的隐性估算题。隐性估算题在教材中是可以保留的，因为它可以培养学生判断是否需要估算的能力。

对于显性估算题，其中有一部分题既含有“估一估”这一特征词，问法又是“……够吗”，这样虽然可以引导学生利用估算的方法解决问题，但是为了培养学生自主判断该使用精算还是估算的能力，可以在部分题目的设计中去掉具有明显特征的估计词。另一部分题包含“大约”一词，并且最后需要得出一个数值答案，这类题的题干让学生知道需要利用估算解题，但是并不是所有包含“大约”一词的题都需要利用估算解题，有时题中的数据就是“大约”的，因此答案也是“大约”的。对于后一类题的设计，或许可以参考TIMSS中关于估计的习题，例如，声音传播的速度大约是每秒340米。某爆炸声经过28秒传到某人的耳朵里，则爆炸源距离此人大约多少米？（四个选项分别是12000、9000、8000、6000）这道题的估计结果并不是因为题干所给的数据中带有“大约”，而是需要用一定的估计策略对题中的数据进行处理，并且给出的选项已经明确了本道题就是对学生的估计能力和估计策略进行考查。

三、习题总体分析和建议

（一）习题类型综合化。

教材中的每道习题都只考一个知识点，如果把多个知识点融合在一起综合考查，会更有助于提高学生的估计能力。例如，对2022年版课标中的例18进行改编，增加一个问题：

李阿姨去商店购物，带了100元，她买了2袋面，每袋30.4元；又买了1块牛肉，用了19.4元。她还想买1条鱼，大一些的每条25.2元，小一些的每条15.8元。请帮助李阿姨估算一下，她此时剩余的钱够不够买小鱼？够不够买大鱼？如果李阿姨突然不想买鱼了，那还剩下多少钱？

对于“够不够买小鱼”，需要向上估计已经花的钱，再用100减去已经花的钱；对于“够不够买大鱼”，需要向下估计已经花的钱，再用100减去已经花的钱；“还剩下多少钱”是一道精算题。像这样的综合问题，更有利于学生理解何时需要估计，以及用什么方法进行估计。

（二）情境素材生活化。

要选择学生熟悉的生活情境，让学生在熟悉的情境中下意识地选择估计方式，这样可以有效培养学生的估计意识，让学生在意识驱动下提升估计的主动性，进而提升估算教学的有效性。例如，可提出这种要求：请测量一下自己1步大概有多长，再估计从教室到图书馆大概要走多少步。这道题有一定的活动性，在活动课中，可以让学生更好地体会估计的用处，并且这是与学生息息相关的事情，有利于激发学生的兴趣，也有利于学生在生活中运用估计培养数感和量感。

（三）估计方法多样化。

对于同一题目，可以让学生自由选择估计方式，从而体会估计方法的多样化，而后引导学生归纳总结，拓展学生对估计方法的认知。例如，2022年版课标中的例33：

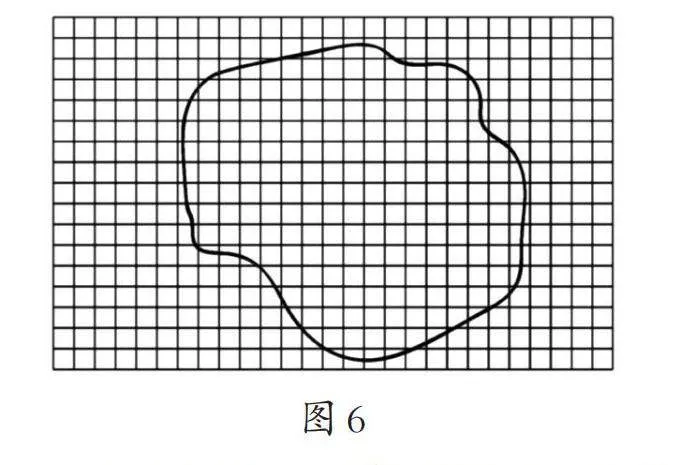
如图6，每个小正方形的面积为1个面积单位，尝试估计曲线所围图形的面积。

对于该题，可以数出图形包含的完整小正方形的数量，再数出图形包含的和边缘接触到的所有小正方形的数量，实际面积就在这两个估计值之间。除此之外，还可以将小正方形等分成更小的正方形，这样可以得到更接近实际面积的估计值。

除了估测类题目，在估算中，估计方法更加多样化，例如，对297×296进行估算。对于这道题，可以用这些方法进行估计：（1）取整，把297和296都变成300再相乘；（2）截取，把297和296都变成290再相乘；（3）补偿，一个取为290，另一个取为300再相乘。估算方法的多样化，估算结果的不唯一性和开放性，也是估算与精算的重要区别。

参考文献：

[1]陈丽兰，刘鸣，曹景明.儿童估算策略选择研究述评及展望[J].数学教育学报，2009，18（3）.

[2]董奇，张红川.估算能力与精算能力：脑与认知科学的研究成果及其对数学教育的启示[J].教育研究，2002，23（5）.

（作者单位：华中师范大学，深圳大学数学科学学院）