店铺销量预测方法的分析与研究

摘 要：本研究旨在分析和研究店铺销量预测的方法，通过介绍一般的预测步骤，以及利用图表趋势预测法、时间序列预测法（指数平滑法）和机器学习方法建立模型对店铺销量进行预测时发现：图表趋势预测法和时间序列预测法（指数平滑法）适用于简单的销量预测，而机器学习方法在处理复杂关系和大规模数据时更具优势。因此，选择合适的方法取决于数据的特点和预测的需求。本研究为店铺销量预测提供了重要的指导和参考，帮助企业做出准确的销量预测，并为库存管理、生产计划和业务决策提供支持。

关键词：店铺销量预测；图表趋势预测法；时间序列预测法；指数平滑法；机器学习方法

一、引言

在竞争激烈的市场环境中，商家需要根据市场需求合理安排产品的生产和销售，以增加利润并保持竞争优势。然而，销量的波动性和不确定性经常使商家面临挑战，因此准确地预测店铺销量成为了迫切需要解决的问题。过去几十年来，学术界和业界对店铺销量预测进行了广泛的研究和实践，提出了许多不同的方法和模型。为了更好地应对市场变化和提高企业的运营效率，通过分析历史数据和相关因素，实现店铺销量的准确预测可以帮助企业做出更加科学的决策。本文将从店铺进行销量预测的步骤，销量预测的不同方法为例，比较各种预测方法的特点，提出销量预测模型，以期为企业决策提供辅助参考依据。

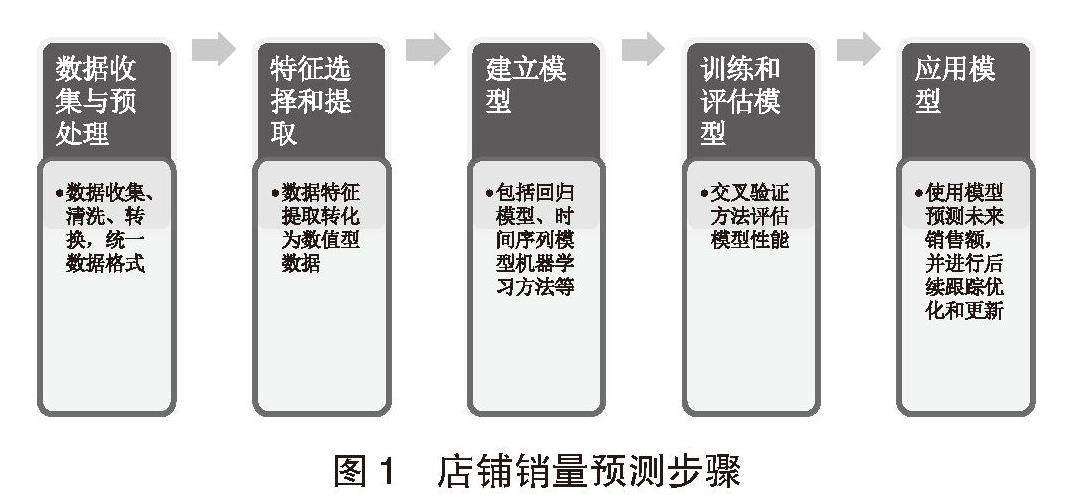
二、店铺进行销量预测的一般步骤

1.数据收集和预处理

首先，需要从各个来源收集店铺销售数据，如历史销售记录、网上购物平台数据、市场调查数据等。然后对这些数据进行清洗、转换和归一化处理，以消除噪声和异常值，并确保数据格式统一和可用。

2.特征选择和提取

在准备好的数据中，需要挑选出对销售额有影响的关键特征，例如商品类别、价格、促销活动、季节因素等。通过使用特征提取方法，可以将这些特征转换成为可以处理的数值型数据。

3.建立模型

经过数据预处理和特征提取之后，可以开始建立预测模型。常见的预测模型有回归模型、时间序列模型、基于机器学习的方法等。

4.训练和评估模型

使用历史销售数据来训练模型，交叉验证方法评估模型的性能，若模型显示较好的性能，便可以用来预测未来的销售额。

5.应用模型

在收集和清洗新数据后，可以将其输入到训练好的模型中，以预测未来的销售额。同时，也需要对模型进行后续跟踪和优化，根据实际情况不断更新模型。

步骤如图1（店铺销量预测步骤）：

三、利用工具建立模型对店铺销量进行预测

店铺产品销售数量往往决定着库存存量，进货量的需求及资金的准备等，一般来说，销售数量与销售额成正比关系，利用科学的方法与手段，对未来一定时期内的市场需求、发展趋势和营销影响因素做预判，可以为店铺营销决策提供服务。

店铺销量进行预测的方法有很多种，通常可以利用通用的Excel工具进行辅助的预测分析，此工具中可以采用图表趋势预测法、时间序列预测法、德尔菲法、GROWTH函数等进行店铺销量预测。

本文采集了某店铺2010—2021年的销售数据，采用图表趋势预测法、时间序列预测法对店铺未来一年的销量进行预测。从而对模型预测的准确性做一些对比。

以下（表1：店铺2010—2021年服装销量统计表）是某店铺在收集和清洗新数据后，得出的2010—2021年销量数据，运用各种模型，预测店铺2022年的销量数据：

使用 Excel打开表1，选中2010—2021年的年份和服装销量数据，利用“图表”组中“折线图”工具完成12年的折线图制作，如图2（店铺2010—2021年销量变化趋势图）所示：

1.利用图表趋势预测法来预测店铺销量

图表趋势预测常用方法包括：线性趋势线预测、指数趋势线预测、多项式趋势线预测等；本文先采用线性趋势线进行销量预测，基本流程为：通过给定数据制作折线图，观察图表形状来添加线性趋势线，利用趋势线外推计算预测值，具体步骤是：在“分析”组中选择“线性趋势线”工具，做前推1年的销量预测，画出趋势线如图3（店铺销量折线图添加线性趋势线）所示：

通过查看预测公式，通过添加线性趋势线后得出一次方程y=2506，x=2977.9，把2022年x为第13个年份代入方程计算，得出销量y=29600.1，结果取整后得出2022年销量预测值，把销量预测结果填入表2（2022年销量预测值）中，预测2022年销量为29600（单位：件）。

2.利用时间序列预测法（指数平滑法）预测店铺销量

时间序列预测法是一种用来预测未来发展趋势的方法，它有两个基本原理：首先，考虑到事物的发展是有连续性的，通过分析过去的时间数据，可以推测出未来的发展趋势；其次，还考虑到了偶然因素引起的随机波动。为了消除这些随机波动的影响，可以使用历史数据进行统计分析，并对数据进行适当的处理，以便更好地预测未来的趋势。常用的方法包括预测季节性波动、使用移动平均公式，以及使用指数平滑法进行预测等。

对表1中的店铺销售数据预测，采用指数平滑法预测，通过计算指数平滑值，并结合适当的时间序列预测模型，可以对某个现象的未来进行预测。指数平滑是一种方法，先使用过去的数据平均计算一个平滑值，然后将这个平滑值与其他预测模型结合起来，以得出对未来的估计。这种方法考虑了过去数据的权重，更加重视最近的数据，因此在预测未来时更加注重最新的趋势。通过这种方式，可以更好地预测未来趋势，并做出相应的决策，重点是需要设置出合理的平滑系数，因为不合理的平滑系数预测出的结果，与实际值相比会相差很多。本文中首先对店铺预测销量设置平滑系数为经验值0.3，然后使用“规划求解”工具再分析出最佳平滑系数，计算出最优解，从而预测出2022年的店铺销量：

首先，在Excel中设计出利用指数平滑法预测销量需要的表格内容，如图4（店铺2010—2021年服装销量表）所示。

然后计算图4中表格各项内容：

图4左侧C列销售预测值计算：首先用Average函数计算出2010年的销量预测值，为2010—2017年的算术平均值，2011年开始，插入公式“=$H$1*B2+（1-$H$1）*C2”进行销量预测值计算，并用公式填充向下填充至2022年销售预测值；

图4左侧D列预测误差计算：预测误差均为销量预测值与销量实际值之间的差额；

图4右侧H列中实际销售量的平均值计算：为2010—2021年销售实际值的算术平均值；

图4左侧E列预测误差平方和计算：用公式“=（D2^2+（C2-$H$2）^2）/12”计算出2010年预测误差平方和，拖动填充柄至E13单元格，填充数据；

图4右侧E列预测误差的总平方和计算：用求和函数计算出E列2010—2021年预测误差平方和得出结果。

以上计算结果如图5（店铺2022年服装销量预测表）所示：

选取年份、销量实际值和销量预测值，最终形成折线图可视化效果，如图6（店铺2010—2021年实销与预测对比图1）所示：从图5可以看出，店铺预测销量设置平滑系数为经验值0.3时，销量预测值与销量实际值差距较大。

3.使用“规划求解”工具分析出最佳平滑系数，计算最优解，预测2022年店铺销量

Excel中，有一个功能叫作“规划求解”，它不是默认显示在Excel工具栏上的，需要手动加载。通过使用“规划求解”，可以找到工作表上某个单元格（称为目标单元格）中公式的最佳值。这里的公式指的是单元格中的一系列数值，可以是单元格引用、名称或者运算符的组合，它们可以生成新的值。

“规划求解”会根据目标单元格公式的相关性，对一组与其直接或间接相关的单元格中的数值进行调整。通过改变这些数值，最终可以得到目标单元格公式所期望的结果。在创建模型的过程中，可以给“规划求解”中的可变单元格应用约束条件。约束条件是一些限制条件，可以被应用于可变单元格、目标单元格或者与目标单元格直接或间接相关的其他单元格。这些约束条件可以引用其他会影响目标单元格公式的单元格。使用“规划求解”，可以通过改变其他单元格的数值，确定某个单元格的最大值或最小值。之前在预测销量时使用的平滑系数，是按经验值0.3，现在需要用到规划求解解出店铺最佳的平滑系数值，从而达到更精确预测销量的目的。

具体步骤实施如下：

在Excel中选择加载宏，选中“规划求解加载项”，如图7（加载规划求解加载项）所示：

加载成功后，在Excel数据菜单选项卡“分析”组中就能见到“规划求解”选项；

在“规划求解参数”对话框中，设置目标单元格为“预测误差总平方和单元格$H$3”，设置可变单元格为“平滑系数单元格$H$1”，需要预测误差总平方和此时为最小，因此选中“最小值”单选按钮，添加约束条件分别设置可变单元格$H$1<=1和$H$1>=0，点击求解后，如图8（规划求解参数设置）所示：

在弹出的“规划求解结果”对话框中，选中“保留规划求解的解”，单击“确定”，如图9（规划求解结果）所示。

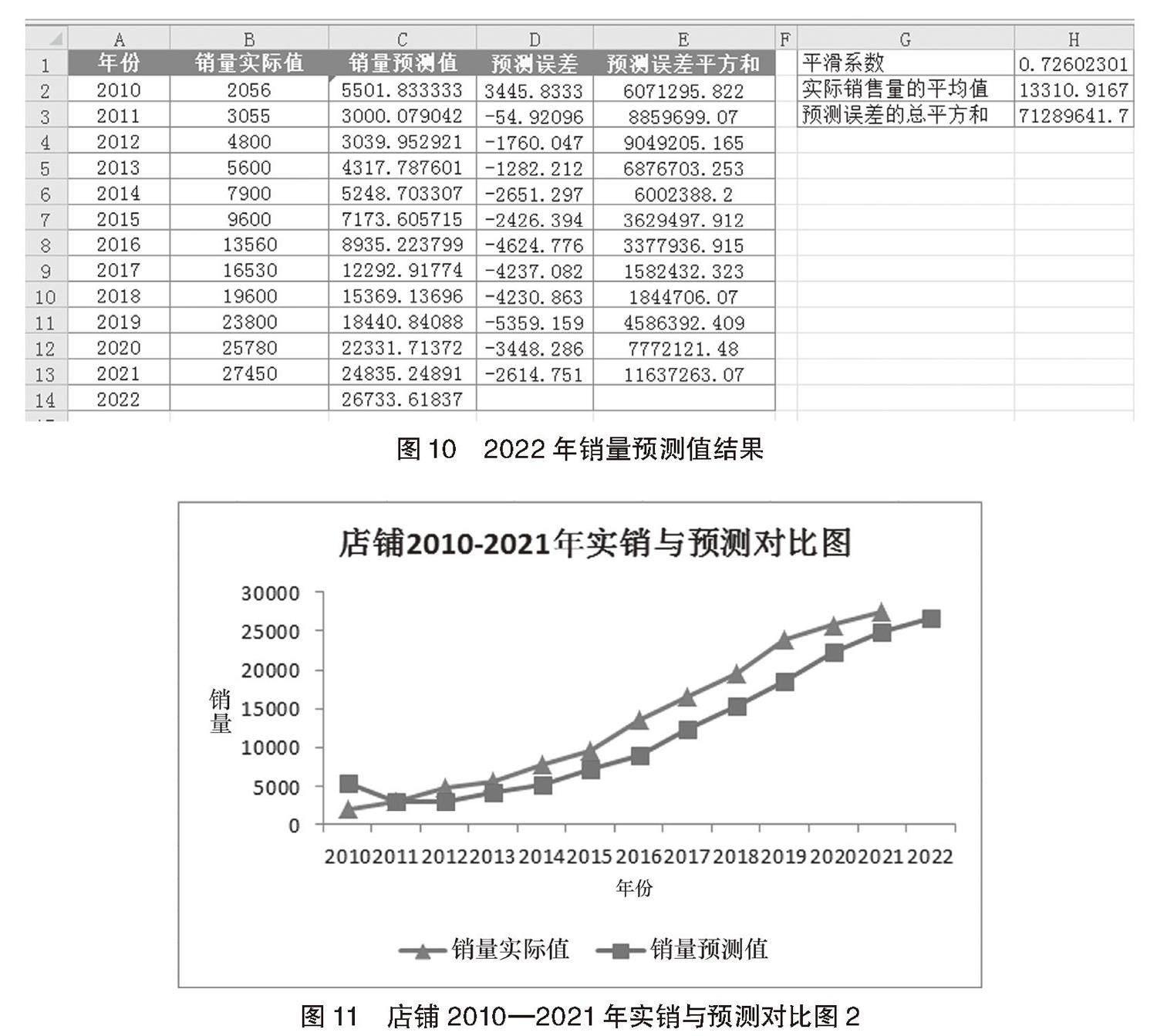
求解以后的结果得出最佳平滑系数应为0.72，预测误差的总平方和为71289641.69，得出2022年销售预测值为26733.61745（约为26734件，取整数值），如图10（2022年销量预测值结果）所示。

选取年份、销量实际值和销量预测值，最终形成折线图可视化效果，如图11（店铺2010—2021年实销与预测对比图2）所示：从图11可以看出，通过“规划求解”分析出的平滑系数更加合理，销量预测值与销量实际值差距较小，通过此法，能达到更精确的预测销量的目的。

4.使用机器学习方法预测2022年的销售数量

将2010—2021年的历史销售数据作为训练集，并利用这个训练集建立一个回归模型，以预测2022年的销售数量。

以下是使用Python中的scikit-learn库进行线性回归的实现：

import numpy as np

from sklearn.linear_model import LinearRegression

#历史销售数据

years = np.array（[2010，2011，2012，2013，2014，2015，2016，2017，2018，2019，2020，2021]）

sales = np.array（[2056，3055，4800，5600，7900，9600，13560，16530，19600，23800，25780，27450]）

#将年份转换为二维数组

X = years.reshape（-1，1）

#创建线性回归模型并进行训练

model = LinearRegression（）

model.fit（X，sales）

#预测2022年的销售数量

predicted_sales_2022 = model.predict（[[2022]]）

print（"2022年销售预测数量："，predicted_sales_2022）

根据运算结果，预测2022年的销售数量为：28268.75件（约为28269件，取整数值）。此模型是基于线性回归模型的简单预测，并且假设销售数据具有一定的线性趋势。实际的销售预测可能需要考虑更多特征和复杂的模型，以及其他影响因素，如市场趋势、竞争情况和宏观经济因素等。

四、结语

通过数据分析预测店铺未来销量是一种可行的手段，通过销量预测可以进一步预测成本和销售额及利润，从而对店铺目前影响销量的各种因素进行分析，最终找到提升销量、销售额、利润的各种方式及手段，利润最大化，也是每个店铺经营者的最终目标。

采用图表趋势预测法中线性趋势线预测和采用时间序列预测法（指数平滑法）预测店铺销量是常用的两种预测方法，各有利弊。

（1） 采用线性趋势线预测法预测销售量，线性趋势线是用于简单线性数据集的最佳拟合直线，线性趋势线预测法较简单，只需通过已产生年份销量画出销量折线图，添加趋势线，显示公式，通过查看预测公式，将预测年份和已知开始年份相减的差值带入公式计算，即可得出预测年份的销量预测值，是一种简单的一次方程计算。

（2） 采用时间序列预测法（指数平滑法）预测，指数平滑法是一种常用时间序列预测方法，原理是通过计算指数平滑值，结合适当的时间序列预测模型预测未来现象的发展趋势。在指数平滑法中，每一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均值。平滑系数是指数平滑中的一个常数，可以将其记作β。通过选择适当的平滑系数β值，进行指数平滑预测，以使预测值与实际值之间的平均误差最小化。平滑系数β的取值范围通常在0到1之间（0<β<1），不同的取值将会对预测结果产生不同影响。

（3） 通过指数平滑法，可以对未来趋势进行预测，并根据实际情况选择适当的平滑系数，以获得更准确的预测结果。理论上来说，平滑系数β越趋近于0，预测得出的结果会与实际值越接近，得到的结果也越理想，β到底取值为多少，最简单直接的手段之一，是采用经验判断进行β取值，凭借数据分析预测人员的个人经验，选择适当的平滑系数β值很重要。如果β值较小，平滑作用会更强，这意味着对预测结果的调整会比较小，对实际数据的变动反应会比较迟缓。换句话说，会更加稳定，更不容易受到短期波动的影响。相反，如果β值较大，对实际值的变化就会更敏感，这意味着对预测结果的调整会比较大。同时，对近期的数据更加依赖，更容易受到短期波动的影响。

（4） 因此，选择合适的平滑系数β值，需要权衡稳定性和敏感性之间的关系，较小的β值适用于平稳的数据，对长期趋势有更好的预测能力；而较大的β值适用于快速变化的数据，能够更快地反应最新的变动情况。根据具体情况，可以选择适合的β值进行预测，并根据实际结果进行调整。采用经验值判断的依据是，当时间序列相对平稳时，可取较小的平滑系数；当时间序列波动较大时，应取较大的平滑系数。本文以年份的连续自然年度为时间序列，照理来说是时间序列是较平稳，可以采用经验判断进行取值。年份时间序列为自然年，变化规律平稳，β取值可以在0.1～0.4，所以最初取值平滑系数β值为经验值0.3，进行销量预测的计算，但是实际计算出的结果对比发现，销量预测值与销量实际值差距较大，通过实际计算，选择误差最小的年份2012年，误差最大的年份2019年为区间范围计算，得出结果误差范围在15.8%～42.5%，实际与预测值误差非常大，所以在实际操作店铺过程中仅能参考，并不能作为销售目标下达任务的依据。

（5） 之后，采用“规划求解”方法求解最合理的β值，通过规划求解，求出最佳平滑系数为0.7之后进行预测销量，选择误差最小的年份2011年，误差最大的年份2019年，进行区间范围计算，得出结果误差范围在1.7%～22.5%，误差明显减小，那么预测未来年度销量选择在误差范围销量区间之间，就有实际参考价值，可作为未来年度销量完成任务下发及销售额考核依据。

最后，用机器学习方法预测2022年的销售数量，发现预测数据和前面指数平滑法的预测结果有较大差别，造成的原因可能为以下两点：其一，机器学习方法通常需要大量的数据进行训练，数据需求量较大，才能获得准确的预测结果，如果可用的历史销售数据较少，可能会对预测的准确性造成影响。其二，机器学习方法的预测结果会受限于数据质量和特征选择，数据质量的影响包括缺失值、异常值和噪声等。此外，正确选择和提取相关的特征也是影响预测准确性的重要因素。

综合来说，机器学习方法在预测销售数量方面具有较高的灵活性和准确性，但需要充分的数据支持和专业知识指导，同时也要注意数据质量和特征选择的问题。

参考文献：

[1]北京博导前程信息技术股份有限公司.电子商务数据分析概论[M].北京：高等教育出版社，2020.

[2]ZHANG，J.，LI，Y.，&LIU，Y.Sales forecasting of retail stores based on ARIMA and LSTM.International Journal of Computational Intelligence Systems，2020，13（1），1745-1757.

作者简介：段亚楠（1979— ），女，硕士，昆明工业职业技术学院，副教授，教研室主任，研究方向：计算机应用，电子商务数据分析。