基于QUBO模型的信用评分卡组合优化研究

许宏飞 牟玲星 许文杰 邓姗姗 唐亚林

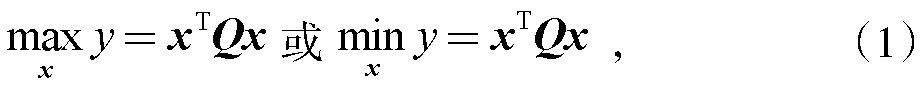
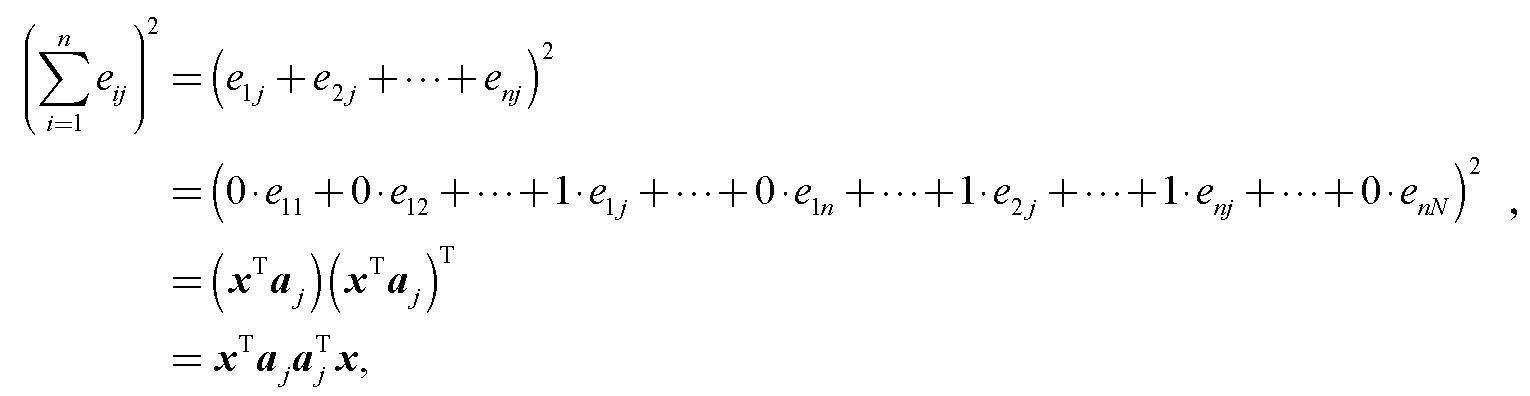
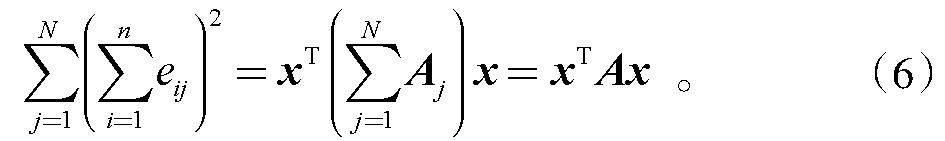
摘  要：银行贷款审核制度对于保障银行财产安全、防范信贷风险和维护金融市场秩序具有重要作用。为提高审核效率和准确性，该文引入二维0-1变量，构建选择1张信用评分卡和3张信用评分卡的银行最大收益模型。借助变量线性组合的方程将不等式约束转变为等量约束，通过换元法将二维变量表示为一维变量，利用0-1变量的性质添加惩罚项将目标函数转化为无约束的QUBO模型。应用模拟退火算法进行快速求解并为银行信用贷款资格审核工作提供指导。

关键词：信用评分卡；最大收益模型；0-1二值变量；QUBO模型；银行信用卡

中图分类号：O29      文献标志码：A          文章编号：2095-2945（2024）19-0043-04

Abstract： Bank loan audit system plays an important role in ensuring bank property safety， preventing credit risk and maintaining financial market order. In order to improve the efficiency and accuracy of auditing， this paper introduces a two-dimensional 0-1 variable to construct a bank maximum return model which selects one credit scorecard and three credit scorecards. With the help of the equation of linear combination of variables， the inequality constraints are transformed into equivalent constraints， the two-dimensional variables are expressed as one-dimensional variables by the substitution method， and the objective function is transformed into an unconstrained QUBO model by adding a penalty term according to the properties of 0-1 variables. The simulated annealing algorithm is applied to solve the problem quickly and provide guidance for the bank credit loan qualification verification.

Keywords： credit scorecard; maximum return model; 0-1 binary variable; QUBO model; bank credit card

银行通过历史数据的学习制定审核规则对客户进行信用贷款评估，这些规则称为信用评分卡[1-2]。在信用贷款审核过程中银行追求提高信贷效率和降低信贷风险，基于此研究人员发布了一些方法帮助银行进行审核。例如，陆凌[3]根据调查数据使用逻辑回归和Xgboost预测贷款客户违约概率。陈战勇[4]基于人人贷平台数据，使用机器学习算法进行特征变量筛选，建立融合权重证据的信用评分卡模型用于预测借款客户的违约情况。但是当数据量比较大时机器学习算法计算量较大，计算代价较大。QUBO模型[5-7]是一种用于解决组合优化问题的二次无约束二值优化模型，可以在量子计算机硬件上进行毫秒级的加速求解，这种模型和加速方式被看好将在未来各行业中得到广泛的实际应用[8]。本文将多约束的信用贷款评估模型转化为QUBO 模型求解可以快速完成评估，为银行贷款审核提供帮助。

1  问题描述

在银行信用卡和贷款业务中，客户在获得信用或贷款资格之前需要通过审核规则进行信用评定。评定过程为通过信用评分卡的组合规则对客户打分，不同的评分卡在不同的阈值下，对应不同的通过率和坏账率。银行通过率越高，获得的利息收入越多，但也伴随着更高的坏账风险。银行的最终收入等于贷款利息收入减去坏账损失。

工作人员设置了100张信用评分卡，每张卡有10个阈值选项，总共有200列数据[9]，其中t1到t100代表每个评分卡的10个通过率选项，h1到h100代表每个评分卡的10个坏账率选项。

建立数学模型研究以下问题。

问题1：在给定的100个信用评分卡中选择1张评分卡及其对应的阈值，使最终收入最大化。

问题2：从给定的100个信用评分卡中任选取3种评分卡，并设置它们的阈值以使最终收入最大化。

2  优化模型建立与QUBO模型转化及求解

2.1  QUBO模型基础知识

QUBO模型描述优化问题的数学公式为

式中：x是二值变量组成的列向量，Q是对称矩阵或上（下）三角矩阵，下面给出一个优化问题转化QUBO模型的例子，考虑优化问题。

进一步可以简记为式（1），容易求得最大值在（x1，x2，x3=（0，0，1）处取到。

QUBO模型是一类被认为是NP难的问题，精确求解器（如CPLEX和Gurobi）很难在除了小问题之外找到最优解。幸运的是，现代元启发式方法能够在合理的时间内找到高质量但不一定是最优的解决方案[7]，这为经典计算和量子计算的结合提供了有价值的可能性，QUBO模型可以自然地用来解决各种优化问题。此外，许多与QUBO模型看似无关的问题也可以重新表述为QUBO模型。本文接下来将带约束的信用评分卡优化模型转化为QUBO模型求解。

2.2  1张信用评分卡优化模型与QUBO模型转化及求解

问题1：需要选择使得银行获得最大收入的信用评分卡及阈值组合。最终收入可以表示为贷款利息收入与坏账损失的差。设有N种信用评分卡，每种信用评分卡对应有n个阈值，引入0-1变量eij，eij=1表示选择组合阈值i和信用评分卡j，反之不选择阈值i或信用评分卡j。设H为贷款总资金，r为利息收入率，tij为组合阈值i和信用评分卡j的通过率，hij为组合阈值i和信用评分卡j的坏账率。g为贷款收入。最优组合的收益表示

为了将约束条件整合到目标函数表达式中，引入惩罚项将式（2）化为无约束形式

2.3  3张信用评分卡优化模型与QUBO模型转化及求解

2.3.1  约束条件的矩阵形式

在实际场景中可能选择多张信用评分卡和阈值组合一起对贷款客户信息信用评定，问题2要求选择3张信用评分卡，有

那么

根据式（4）不难推出

为了写成矩阵形式，设

式中：aj=（0，0，…1，0，…，1，…，1…，0）T，列向量的第j，（N+j），…，Nn-1+j个分量为1，其余为0。记ajaj=Aj，则选择不同信用评分卡约束可表示为

2.3.2  3张信用评分卡优化模型的建立及QUBO模型转化

贷款收入等于贷款利息收入减去坏账损失，根据约定[9]多种信用评分卡组合的总通过率为所有信用评分卡通过率的乘积，总坏账率等于所有信用评分卡对应坏账率的平均值。

3张信用评分卡组合的通过率即为eijtij中不为0的3个之积，而选择哪3个是未知的，且没有选中的信用评分卡eijtij一定为0。而

因此3张信用评分卡卡最优组合的收益为

求解式（8）可以转化为求解以下优化问题

转化eij为单下标变量并重新编号eij=x，lntij=lntk，hij=hk，k=N（i-1）+j，由xk为0-1变量，x=xk，带入式（6），上面的模型可化为

舍掉常数项，QUBO形式为

2.3.3  QUBO模型的求解

代入N=100，n=10，H=1 000 000，r=0.08及信用评分卡调查数据，选取P为uvT-Λ的最大值，应用模拟退火算法温度设为100 000 ℃，最大迭代次数设为100 000 000，进行多轮求解，求得最小值对应的解x为第108，249，533个分量为1，其他分量为0。

根据eij=xk，k=N（i-1）+j还原可得i=2，l=8；j=6，p=33；k=3，q=49。所以3张信用评分卡收益最大的组合为信用评分卡8和阈值2，信用评分卡33和阈值6，信用评分卡49和阈值3。

3  结束语

本论文利用QUBO模型解决银行信贷客户资格审核问题，以实现银行的最大收益。在3张信用评分卡组合的优化模型建立中，以各信用评分卡为底数，以二维0-1变量eij指数连乘表示信用评分卡组合的总通过率，以选中3张信用评分卡的平均坏账率表示总坏账率，建立3张信用评分卡组合的最优收益模型，通过变量线性组合的方程将难以整合到惩罚项的不等式约束转化为等号约束，再将二维变量简化为一维变量，成功将带有连乘项和连加平方项的目标函数简化为同解的只具有连加项的目标函数，并将其转化为无约束的QUBO模型进行求解。本文重点介绍了1张信用评分卡和3张信用评分卡的情况，其他情况类似，不再详述。研究结果表明，在使用QUBO模型进行求解时，只需关注Q矩阵部分，求解速度快。尤其是在解决1张信用评分卡的情况下，最优解恰为Q矩阵主对角线的最小值。总的来说，QUBO模型易于操作和求解，并可为银行的信用评估工作提供便捷和支持。

参考文献：

[1] 林治乾，严志辉.信用评分卡在中小企业贷款业务中的应用[J].银行家，2013（2）：77-79.

[2] 丁卫东.信用评分卡在电商小微企业信贷中的应用[D].杭州：浙江大学，2016.

[3] 陆凌.信用风险评分卡模型[D].上海：上海财经大学，2020.

[4] 陈战勇.珠联璧合：基于机器学习的网络借贷信用评分卡模型研究[J].武汉金融，2020（3）：42-50.

[5] PAPALITSAS C， ANDRONIKOS T， GIANNAKIS K， et al. A QUBO Model for the Traveling Salesman Problem with Time Windows[J].Algorithms，2019，12（11）：224.

[6] MORSTYN T.  Annealing-Based Quantum Computing for Combinatorial Optimal Power Flow[J]. IEEE Transactions on Smart Grid， 2023，14（2）：1093-1102.

[7] GLOVER F， KOCHENBERGER G， HENNIG R， et al. Quantum bridge analytics I：a tutorial on formulating and using QUBO models[J].Annals of Operations Research，2022（314）：141-183.

[8] VERMA A， LEWIS M. Penalty and partitioning techniques to improve performance of QUBO solvers[J].Discrete Optimization， 2020：100594.

[9] 2023年第十三届MathorCup高校数学建模挑战赛A题[EB/OL].http：//mathorcup.org/detail/2417，2023.4.13.