基于包络线的防风垃圾桶空间凸轮弧面设计

张贝

摘要：针对目前凸轮的设计方法不能实现某些特殊零部件从动件空间准确动作的设计要求，提出采用包络线方法的凸轮轮廓弧面设计方法，该设计方法可实现凸轮准确控制垃圾桶盖因风力大小改变开度的能力。首先基于凸轮的设计原则，建立简单平面凸轮的包络曲线模型，对包络线方程进行求解，然后利用感风桶风力方向的所在平面建立相应包络线曲线模型，形成相交空间包络曲线簇，而后组集凸轮轮廓点数据，建立平行空间包络曲线簇，通过随后的轮廓点拟合建立平行空间包络曲线簇方程，并考查空间包络曲线拟合方程参数随曲线簇垂直方向坐标的变化，而后通过两组拟合参数建立曲面求解数值方程。该空间凸轮轮廓弧面设计方法可准确设计凸轮的空间轮廓，并能实现凸轮的准确控制。该空间凸轮轮廓弧面设计方法过程连续，求解规范可实现程序移植推广。

关键词：空间凸轮设计；包络线方程；防风垃圾桶；感风桶

中图分类号：TH112.2                文献标志码：A                   doi：10.3969/j.issn.1006-0316.2024.05.009

文章编号：1006-0316 （2024） 05-0064-10

Design of Spatial Cam Surface Used on Windproof Refuse Bin with Envelop Method

ZHANG Bei1，2

（ 1. School of Oceanography， Shanwei Institute of Technology， Shanwei 516600， China;

2. College of Mechanical and Automotive Engineering， South China University of Technology，

Guangzhou 510000， China ）

Abstract：The present cam design method cannot meet the requirements for accurate spatial movement of certain spatial components and followers. An envelope-based cam design method is proposed， which can make the cam to accurately control the openning of refuse bin cover due to changes in wind force. According to cam design principles， cam envelop curve is modeling in simple plane and the envelop equation is solved. Then a corresponding envelop curve is modeling in other plane where the wind direction of the wind sensing bracket is located.. Thus clusters of intersecting spatial envelope curves are formed. To organize cam profile point data， parallel spatial envelop curve clusters are built. With regression of profile point the parallel spatial envelop curve clusters equation is built. The regression parameter is observed with coordinate variation which is vertical to curve clusters. Furthermore the numerical equation is observed. The design mehtod can accurately build cam spatial profile and realize accurate control of the cam. The design method has a process and the solution specification can achieve program portiing and promotion.

Key words：spatial cam design；envelop equation；windproof refuse bin；wind sensor

目前，针对垃圾桶的研究主要是基于应用方面，大部分垃圾桶的研究主要集中在垃圾分类[1]、提升垃圾桶智能化水平[2]、以及特殊功能的垃圾桶设计[3]。垃圾分类主要采用图像识别技术，垃圾桶智能化和特殊功能垃圾桶的设计则需要借助一些传感器等硬件进行系统设计。对于特殊功能垃圾桶的设计采用硬件系统的方法固然自动化程度高，但是这些硬件系统在污染介质里长期使用会生成较高的运维成本。另外，所设计系统包含电源，是耗能产品，在潮湿污染物盛放和户外工作的多粉尘条件下可靠性会显著减小。在多风多雨且存在污染介质的环境中使用硬件系统可靠运行是比较困难的。

在南方临海地区的垃圾桶一般存在于多风的环境中，清洁人员一般需要将垃圾桶盖关闭，以防止因风力较大而产生较多的垃圾飘散。这对使用垃圾桶的居民或行人造成了不便，他们会因为厌恶拨弄垃圾桶盖的操作而随意在附近的地面上丢弃垃圾，造成了垃圾清洁的困难。如果采用以往的硬件系统，不但需要额外的运维人员，而且可靠性非常低，因此需要一种机械式自动防风垃圾桶的产品设计。

通过风力的大小改变垃圾桶盖的开度更能使防风垃圾桶适应南方临海多风地区的气候环境。这种垃圾桶的设计需要一个关键零件，就是控制垃圾桶盖的凸轮。

凸轮轮廓曲线的求解是凸轮设计的关键。凸轮轮廓曲线的求解主要有图解法[4]、拟合法[5]和解析法[6]，大部分凸轮研究主要聚焦凸轮的某些特征值如曲率半径[7]、压力角[8]，有些是凸轮的特殊应用[9]，还有些关注非凸轮廓的凸轮设计[10-11]，凸轮轮廓难以用较准确的数学刻划。因此很少有针对凸轮轮廓本身的数学形式研究。

凸轮轮廓本身的数学形式研究对于这种防风垃圾桶的凸轮设计非常重要，因为这种凸轮设计不是从以往从动件的运动规律推算凸轮的升程变化规律，而是根据风力大小摆动凸轮作用于垃圾桶盖的逆向设计过程。按照以往的图解法逐点描述升程曲线将会造成空间凸轮弧面设计的困难，逐点图解难以准确描述凸轮的空间轮廓，进而对后续凸轮产品的工程绘制和加工生产带来困难。

本文采用垃圾桶盖运动形成的直线簇方程求解凸轮轮廓的包络线方程，从平面的凸轮轮廓曲线的数学描述拓展到空间平面的凸轮轮廓曲线上，然后建立平行空间包络曲线簇方程，最后通过两向拟合参数计算出曲面方程组的数值解，形成满足设计要求的空间凸轮轮廓弧面。

1 简单平面凸轮的包络曲线模型

依据风力大小控制垃圾桶盖开度的方法如图1所示。这里只考虑迎面风，背向风由于对垃圾的扰动较小，可暂时不予考虑。图1所示为防风垃圾桶机械系统。感风桶是感受风力的元件，由圆形桶体构成，以保证迎面风180°内的风力对垃圾桶盖具有同等的作用，桶体表面可设计成小孔洞结构以增加风力的感知能力[12]。感风桶由摆杆支撑，摆杆的一端固定感风桶，另一端固定有控制凸轮，摆杆的中间设有摆杆支点，摆杆支点与垃圾桶桶体通过杆架固定连接。摆杆支点两侧的臂长比可设定合适数值，以保证感风桶的迎风面积小于垃圾桶盖面积仍能灵活关闭和开启垃圾桶盖，这样所设计的机械系统总体尺寸会非常小。摆杆在感风桶和摆杆支点之间设有摆杆复位拉压弹簧，以保证大风过后感风桶和摆杆能恢复到初始位置，这时垃圾桶盖达到所设定的最大开度。垃圾桶盖下面设有复位压缩弹簧，它是保证凸轮与垃圾桶盖从动件力锁合的元件。

图1的工作原理为：如果有迎面180°内的大风超过所设定的风力阈值，则感风桶通过风力的传递压缩摆杆复位弹簧，带动摆杆绕摆杆支点转动，摆杆另一端控制凸轮旋转而压缩垃圾桶盖复位压缩弹簧，从而准确控制垃圾桶盖的开度，使垃圾桶盖在风力较大时关闭垃圾桶盖，风力中等时垃圾桶盖停留在小开度状态，风力较小和无风时垃圾桶盖维持在最大开度状态。

凸轮轮廓线依据凸轮图解反转法设计[13]。所谓反转法就是在设计凸轮轮廓线时，可假设凸轮摆杆静止不动，而使垃圾桶盖相对于凸轮摆杆作反转运动，同时又绕垃圾桶铰链做旋转的关闭运动，作出垃圾桶盖在这种复合运动中的一系列位置（图2中1～6，相应的摆杆位置为1～6），则能够内包络所有的垃圾桶盖所在直线的曲线即为凸轮的轮廓线。

1～6为垃圾桶盖的位置；1～6为摆杆凸轮的径向位置。

首先建立平面坐标系，因为后续的解析推导非常复杂，所以采用具体数值进行参数拟合，结果形式较为直观，且该方法采用python编程计算，设定参数的改变不影响程序流程。如图3所示，不妨设垃圾桶盖的最大开度为75°，垃圾桶盖被y轴所截断的长度AB为100（这里的100和后面图3里的120等数字不代表具体的长度，而是一个相对参考量，不具有毫米或厘米等具体长度单位的测量属性，角度数字除外），以垃圾桶盖所截左端点A对应x轴零点位置，这样可以保证包络线的x坐标基本上在正值范围，垃圾桶盖接触面右端点B坐标为（100sin 15°， 0）。设摆杆支点的横坐标与B相同，即100sin 15°。

由图3、图4所示垃圾桶盖反转法运动关系可知，设摆杆上O1B的长度为120，则垃圾桶盖反转法运动时垃圾桶盖所在直线上一点B位于以摆杆支点O1为圆心以120为半径的圆上。如图4所示，设摆杆等速旋转75°时凸轮将垃圾桶盖等速关闭，垃圾桶盖最大开度也是75°。在整个反转的运动过程中，垃圾桶盖一方

面绕摆杆支点O1作逆时针旋转运动，这时要求垃圾桶盖旋转75°；一方面又要完成垃圾桶盖关闭到垃圾桶上的动作，垃圾桶盖关闭需要完成75°的逆时针旋转角度；所以完成整个动作，摆杆需要逆时针旋转75°，垃圾桶盖需要旋转2×75°。同理，凸轮摆杆逆时针旋转角度为α，垃圾桶盖所在直线会逆时针旋转2α。α的范围为0～75°。表1为所设计机构的预设参数。

根据以上建立的直角坐标系和预设参数利用直线的点斜式方程（点的坐标可采用B点的运动坐标，斜率可根据垃圾桶盖所在直线旋转的角度进行计算）可以推出垃圾桶盖所在直线的通式为式（1）。

将式（1）整理为标准形式得到式（2）。将式（2）对α求导可得式（3）。

联立式（2）（3）消去α即可得出包络线的方程[14-16]，但解析式非常复杂，因此从式（3）可得出x与α的关系如式（4）所示。

再根据式（1），利用四次多项式python拟合，可得出x、y的函数关系式为：

（5）

其中参数如表2所示。该曲线显示的平面凸轮轮廓如图5所示。图5的凸轮轮廓曲线光滑连续且凸函数特性好，证明拟合精度适当。

2 相交空间包络曲线簇

由于风向并不总是正面吹向垃圾桶，所以需要考虑风向与垃圾桶正面存在一定角度的情况。这时就有若干个平面凸轮轮廓曲线，它们所在的平面是一簇相交平面。如图6所示，不妨设这一簇平面中每一个平面的y轴为yt轴，x轴为xt轴，平面中的坐标原点为Ot。相交平面的交线设为z轴，z轴经过摆杆支点，y轴为垃圾桶正面反方向，空间坐标系的原点为O。这样平面凸轮轮廓曲线的所有平面关系均能应用于空间凸轮轮廓设计。

角度的关系如图7所示。角度说明见表3。垃圾桶盖正面的最大开度设为75°，垃圾桶盖在xtOyt平面中的最大开度为β。凸轮摆杆在xtOyt平面内的摆角行程为φ，垃圾桶盖从最大开度到关闭行程为β，凸轮摆杆每旋转α角，即走完总行程的α/φ，垃圾桶盖也需要旋转α/φ倍的总行程，对应垃圾桶盖旋转角度为α·β/φ。xtOyt平面与垃圾桶正面方向（y方向）的夹角即xtOyt平面与yOz平面的夹角设为θ。

根据图7中的位置关系，仅研究风向所在平面xtOyt的摆杆与垃圾桶盖的相对位置变化。可得出角度关系为：

（6）

风向所在平面内的垃圾桶盖所在直线通式为如式（7）所示。

将式（7）写成标准形式可得式（8）。将式（8）对求导可得式（9）。由式（9）推出xt的表达式为式（10）。

（7）

（8）

（9）

（10）

通过图7的坐标变换为：

（11）

式中：x的定义域为（-48.04， 48.04）。其具体的散点图形如图8所示。

3 平行空间包络曲线簇

由得出的凸轮弧面数据虽然能看出凸轮弧面的大致形状，但其数据对于三维直角坐标而言不够整齐，不能明确显示数据点空间位置关于x、y的变化关系，不利于总体曲面方程式的拟合。因此需要将相交空间的包络线簇转变为平行空间的包络曲线簇。

具体方法为：把图8中的散点数据用平行于xOz平面的平面簇进行均匀分割，两个平行

平面之间的散点数据通过以下方程形式拟合：

（12）

由式（12）生成的拟合曲线如图9所示，可以看出凸轮在接近中央平面（x＝0）处的曲线平顺性较好，x值越大的地方会出现曲率较大的点，甚至出现凹函数特征。这说明凸轮在x值较小时控制垃圾桶盖开度的平顺性较好，在x值变大时凸轮控制垃圾桶盖开度的平顺性变差，其压力角和曲率半径的校核会接近临界值，有可能造成冲击，但对于垃圾桶盖的使用场合，其动态特性还是可以接受的。拟合参数μ0、μ1、μ2、μ3、μ4随x的变化如图10所示。

从图10可以看出，μ0、μ1、μ2、μ3、μ4参数的绝对值依次减小，μ0常数项系数为正值，μ1一次项系数为负值，且常数项和一次项系数出现较大的波动，μ2、μ3、μ4绝对值都很小且变化非常微弱，因此拟合方程的高次项对函数值的贡献急剧减小，由于曲面关于x＝0平面对称，所以有些拟合参数呈现双峰形状，如只看x＞0一侧的曲面，拟合方程一定程度上更接近于抛物线方程，但在计算曲面网格点具体数值时高次项因为x、y值的高次幂数值较大而无法忽略。

4 凸轮弧面的数值求解

如果将参数μ0、μ1、μ2、μ3、μ4视为x的函数，则凸轮弧面将会有含两自变量的完整表达，形成了较为完整的数值曲面解。由此可得：

（13）

根据图10中的数据，按四次多项式函数进行拟合，可得：

（14）

其中系数矩阵A为：

（15）

式（15）中的数值以MATLAB格式写出，如9.1596e1表示为9.1596×101。将式（14）和式（12）联立可得曲面方程为：

（16）

也可以写成如下形式：

（17）

根据式（15）代入x、y的具体坐标值，可绘制出如图11所示凸轮轮廓外形，可以看出其

数值曲面与图9所示的曲线簇非常接近。

式（15）中的第i行第j列元素aij参数有些数值绝对值很小，其中第二行和第四行都非常小，这一点与凸轮关于x＝0对称有关，凸轮轮廓是关于x＝0平面的偶函数，所以奇次项应省略取0，则式（15）可简化为式（18）。

根据式（18）可得图12所示凸轮弧面的数值解，可以看出图12与图11基本形状一致，它们之间的差值较小。

（18）

5 讨论

从图11和图12的凸轮曲面形状来看，在凸轮的底部x方向有马鞍形的不平整误差，这不是拟合精度不足造成。对于相交空间曲线簇，形成这种误差的主要原因是不同θ的平面凸轮轮廓曲线并不能保证都相交于一点，甚至有些凸轮曲线可能不相交。但它们都几乎交于一点，因为这些凸轮轮廓曲线都几乎经过这一点。θ较大的凸轮轮廓曲线有可能位于θ较小的凸轮轮廓曲线下侧，这样拟合出来的曲线会形成较大的马鞍形误差，这一点也可以从图10的拟合参数μ0、μ1的变化趋势得到证明。y方向平行的凸轮轮廓曲线也有一定的微凹性，但是不明显，几乎不影响凸轮的运行，为了提高拟合的精度，保留四次的拟合曲线形式，而x方向的马鞍形误差较为明显，又因为凸轮曲面是关于x＝0平面的偶函数，所以改用二次函数进行拟合，即：

（19）

其中系数矩阵A可以表示为式（20）。

式（20）中第二行由于绝对值很小且曲面方程是关于x＝0的偶函数，因此可设第二行所有元素为0，可得式（21）。

式（22）为凸轮轮廓曲面方程。将式（21）代入式（22）可消除马鞍形误差。

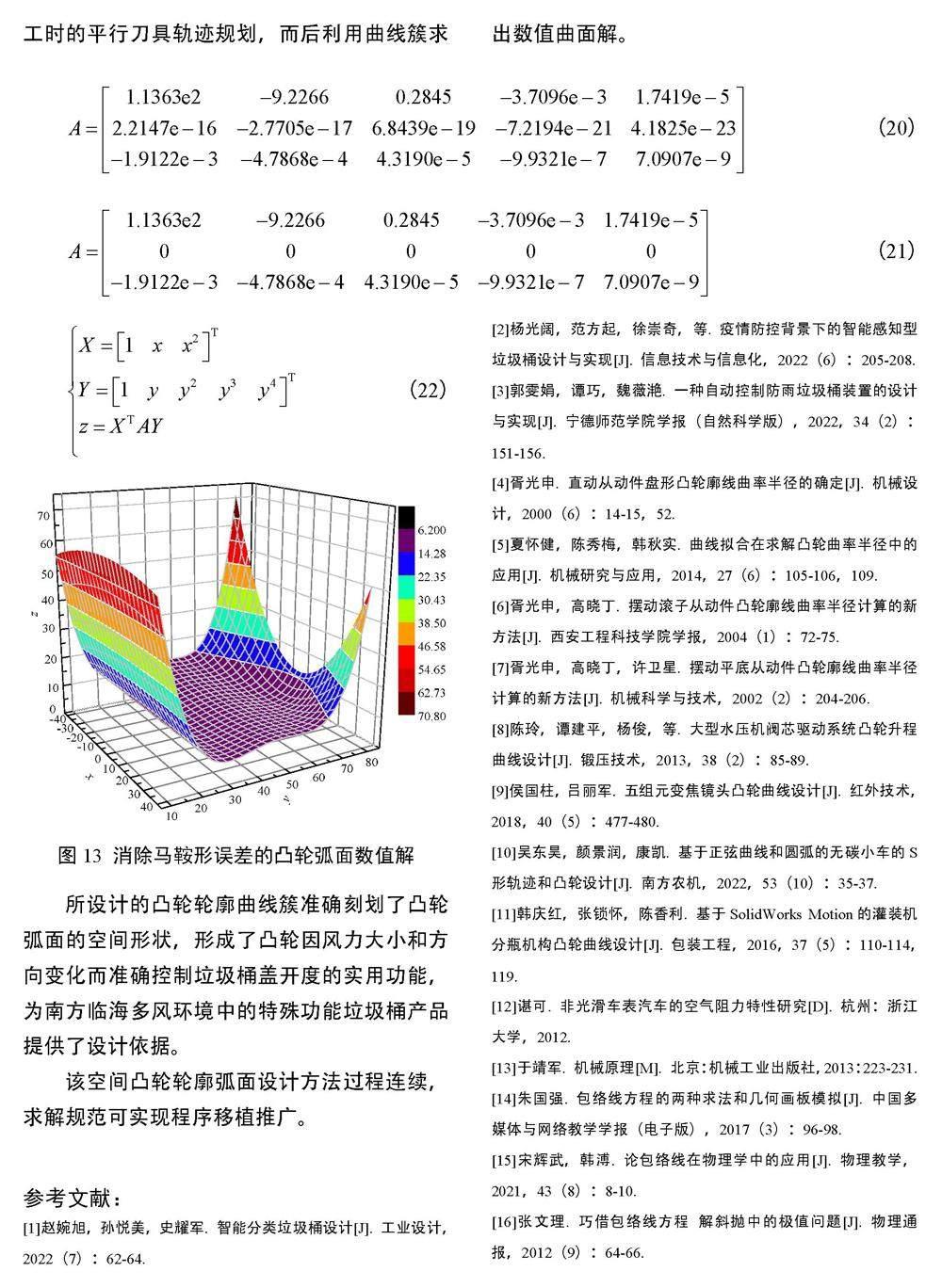
根据式（22）计算得出凸轮弧面的数值解如图13所示。

6 结论

在凸轮轮廓的包络线模型求解基础上建立空间包络曲线簇，该包络曲线簇可用于凸轮加

工时的平行刀具轨迹规划，而后利用曲线簇求出数值曲面解。

（20）

（21）

（22）

所设计的凸轮轮廓曲线簇准确刻划了凸轮弧面的空间形状，形成了凸轮因风力大小和方向变化而准确控制垃圾桶盖开度的实用功能，为南方临海多风环境中的特殊功能垃圾桶产品提供了设计依据。

该空间凸轮轮廓弧面设计方法过程连续，求解规范可实现程序移植推广。

参考文献：

[1]赵婉旭，孙悦美，史耀军. 智能分类垃圾桶设计[J]. 工业设计，2022（7）：62-64.

[2]杨光阔，范方起，徐崇奇，等. 疫情防控背景下的智能感知型垃圾桶设计与实现[J]. 信息技术与信息化，2022（6）：205-208.

[3]郭雯娟，谭巧，魏薇滟. 一种自动控制防雨垃圾桶装置的设计与实现[J]. 宁德师范学院学报（自然科学版），2022，34（2）：151-156.

[4]胥光申. 直动从动件盘形凸轮廓线曲率半径的确定[J]. 机械设计，2000（6）：14-15，52.

[5]夏怀健，陈秀梅，韩秋实. 曲线拟合在求解凸轮曲率半径中的应用[J]. 机械研究与应用，2014，27（6）：105-106，109.

[6]胥光申，高晓丁. 摆动滚子从动件凸轮廓线曲率半径计算的新方法[J]. 西安工程科技学院学报，2004（1）：72-75.

[7]胥光申，高晓丁，许卫星. 摆动平底从动件凸轮廓线曲率半径计算的新方法[J]. 机械科学与技术，2002（2）：204-206.

[8]陈玲，谭建平，杨俊，等. 大型水压机阀芯驱动系统凸轮升程曲线设计[J]. 锻压技术，2013，38（2）：85-89.

[9]侯国柱，吕丽军. 五组元变焦镜头凸轮曲线设计[J]. 红外技术，2018，40（5）：477-480.

[10]吴东昊，颜景润，康凯. 基于正弦曲线和圆弧的无碳小车的S形轨迹和凸轮设计[J]. 南方农机，2022，53（10）：35-37.

[11]韩庆红，张锁怀，陈香利. 基于SolidWorks Motion的灌装机分瓶机构凸轮曲线设计[J]. 包装工程，2016，37（5）：110-114，119.

[12]谌可. 非光滑车表汽车的空气阻力特性研究[D]. 杭州：浙江大学，2012.

[13]于靖军. 机械原理[M]. 北京：机械工业出版社，2013：223-231.

[14]朱国强. 包络线方程的两种求法和几何画板模拟[J]. 中国多媒体与网络教学学报（电子版），2017（3）：96-98.

[15]宋辉武，韩溥. 论包络线在物理学中的应用[J]. 物理教学，2021，43（8）：8-10.

[16]张文理. 巧借包络线方程 解斜抛中的极值问题[J]. 物理通报，2012（9）：64-66.