基于图神经网络的交通流量预测方法研究
薛焱中

摘 要:文章提出了一种新型的交通运输流预测方法。 首先,提出了一个基于时间空间特征的交通流预测模型,其中道路交通流的空间特性的提取是使用图形卷积网络(GCN)进行的。其次,通过一个简单而强大的可变触发周期单元GRU来实现一种随时序改变的道路网络;在此基础上,利用sequence-to-sequence模型对道路各个阶段的时间序列进行了评估,并利用该模式来获取最终的预测结果。最后,以sequence-to-sequence模型为基础,采用了自动编码机制对模型进行了结构优化,使预报准确率有了很大提高。
关键词:交通运输;图神经网络;深度学习;流量预测;自动编码机制
中图分类号:F282;U491文献标志码:ADOI:10.13714/j.cnki.1002-3100.2024.10.021
Abstract: In this paper, a new method for traffic flow prediction is proposed. First, a traffic flow prediction model based on spatial-temporal features is proposed. Here, the extraction of spatial features of road traffic flows is implemented using a graphical convolutional network(GCN). In addition, a simple but powerful variable trigger period unit GRU is used to implement a time-varying road network. Based on this, a sequence-to-sequence model is used to predict multiple phases of the sequence and the final predictions are obtained from this model. Finally, on the basis of the sequence-to-sequence model, the structure of the model is optimized using an automatic coding mechanism, which significantly improves the accuracy of the predictions.
Key words: transportation; Graph Neural Network; deep learning; traffic prediction;automatic coding mechanism
0 引 言
近年来,我国的经济高速增长带来了一系列城市交通问题,包括人均工资水平上升、汽车生产成本增加、道路交通拥堵等。城市快速发展导致人口激增,但城市规划和改善滞后,交通拥堵、环境恶化以及通勤成本的增加,成为市民生活的难题,也引起了政府的重视。为了更好地规划城市交通,节约时间、提高交通流预测的准确性成为学术界关注的焦点。
然而,在交通流量预测方面存在一些挑战,包括道路网络的空间依赖性和长期时间的难以预测性。首先,道路网络的交通流量受空间相关性影响,不同路段之间的关联性复杂,而且下游车流对未来的影响较大,这需要建立基于空间相关性的道路网络模型。其次,交通流量具有高度的实时性,受到工作日、假期、交通高峰期和不可预测事件的影响,因此长期预测较为困难。
有关交通流量预测的研究已经有数十年的历史,当下主要有知识驱动和数据驱动两种研究方法。在运输与运筹学方面,人们经常将队列理论用于仿真交通中的使用者行为。[1]在时序上,目前仍有几种数据驱动的方法,例如,自回归综合移动平均模型ARIMA,即根据所探测到的异常点的时间和空间特征,构建了一种基于异常点的空间和时间特征的异常树。这些因果树的构造,既能反映出时空异常量间的反复互动,又能反映出目前的路网设计中存在的一些不足。[2]另外,卡尔曼滤波方法也是一种新的支持矢量回归方法。[3]传统的时间序列模型都是依靠较为稳定的假定,但是在实际应用中,交通数据常常是非稳定的。
通过不同的传感器采集的速度、体积和密度,可以很好地反映出道路的交通情况。所以,这些数据一般被用来进行流量预报。根据预测的时间长短,可以将交通预测划分为三个规模:短时(5~30分钟)、中期(30~60分钟)、长期(1小时)。大部分常用的方法在短期预测范围内都有很好的效果。归根结底,车流是非常复杂和不确定的,因此,用上述方法进行长时间序列预报是很困难的。
在仿真方面,对交通流量进行预测,必须建立在物理原理和已有的基础上,对其进行全面、细致的建模。[4]然而,为了实现稳定,仿真系统和仿真工具仍需耗费大量的运算能力和熟练的参数设定。目前,由于交通数据的实时获取方式与方式的飞速发展,研究者们开始从大量的历史数据中寻找数据挖掘的方法。
交通预测是以排队理论和模拟为基础的经典交通问题。目前,基于数据的交通预测技术已经引起了人们的广泛重视。但是,目前的机器学习模型不是对数据进行了强烈的平滑假定,如自回归模型或者没有能够解释诸如潜在的空间模型之类的高度非线性的时间相关性[5]。
在交通预测中,卷积神经网络也得到了广泛的应用。有学者将路网转化为具有规律性的二维网格,然后,利用CNN技术,构建了一种新的交通流预测模型。[6]
本文提出了一种基于网络空间关联度的预测方法,旨在解决交通流量预测中的复杂因素和难题。这种时空预测模型不仅对交通流量预测具有重要意义,还可以应用于其他时间和空间的预测问题,为城市交通规划和相关领域提供有价值的理论支持。
1 模型构建
1.1 基于时空特征的交通流量预测模型
1.1.1 交通流预测问题
交通流量预测主要是利用网络中N个相关传感器所观察到的交通流进行预测。用图表来表示传感网络。
(1)
其中,是节点集,是边集。
使用图形的信号来表示在图G中所观察到的交通流量,为各节点的特征数目,是在时刻所观察到的图形信号,那么,交通流预测问题的目标即为一个函数,该函数为,给定一个图,交通量预测问题可以通过将图形信号从过去时间转移到未来时间来表示,如图1所示。
1.1.2 交通流量预测过程
在此基础上,本文提出一种基于时空特性的交通流量预测算法,首先对交通数据进行采集,并对其进行训练,得到最优的特征矢量集,再将其输入到循环神经网络中,利用序列-序列模式进行预测。图2是预测车流的流程图。
1.2 交通流空间依赖建模
1.2.1 问题定义
为方便对模型进行描述,本节本文研究了图卷积网络在交通流量预测中的应用。交通预测是指在一定时期内,根据以往的车辆行驶速度数据,预测某一地区的未来某一时间的路况;由N个测点的M次时间步长测量的历史流量可以看作是的矩阵。
本文提出了一种无向图,用于描述路网中的邻近传感器站的相互关系。其中,是传感器的节点集;是一个边集,它代表了交通网络中各传感器的连通性;如果图G所示的顶点拓扑能够从原始数据获得,则可以利用连通度求出之前不能得到的节点拓扑,在没有求出的情况下,可以根据节点之间的间距来构造邻接矩阵。这样,可以将先前的流量数据集合定义为含有M个图结构的数据帧的G,见图3。
在这个阶段,时空交通预测的问题可以表达如下。T表示预测的时间长度。
1.2.2 用图卷积提取空间特征
卷积神经网络被广泛用于大型和高维的数据集。含有隐性局部特征的交通变量可以使用CNN成功提取其位置和相邻性。GCNs已经成为一个重要的研究领域,因为这可以实现机器学习。一些研究人员创造性地定义了基于频谱分析的图卷积神经网络(GCNN)[7],这种模型可以处理具有任意图结构的数据,且具有与传统 CNNs一样的线性运算复杂性和不变的学习复杂性。因此,在这里,城市交通数据是由图形卷积网络处理的。图形卷积网络的输入是一个三维张量,大小为,来自数据矩阵。
在稀疏图中,采用图卷积技术,只需要很少的可训练参数,就能得到较高的空间信息。图卷积运算可视为一种具有严格位置滤波的地图浏览,利用图卷积法对邻近结点间的信息进行收集、分布。
若无向图具有大小为N的矢量,则在的频谱范围内定义了该图的卷积。拉普拉斯算子,特征值分解,为对角矩阵,为正交阵,s的傅里叶变换是,图形与的卷积[8]定义如下。
(3)
代表卷积操作。基于此,可以用滤波器来定义图关于矢量的卷积,这里的还代表一个对角阵。
(4)
在实际操作中,这个方程相当于对和向量的图形卷积进行计算。
(5)
由此,可以把看作是一个图形的卷积。为减小参数数目和本地化过滤器,可以将限定在一个多项式中。,其中为图的卷积核。接着,可以按以下方式对进行扩展。
(6)
在N个结点的图中,可以用N个具有的矢量构成的矩阵来表示。这样,对,对具有的核张量的卷积操作如下。
(7)
其中,和代表输入和输出信道的数目。
每个站点在路网中的位置对车速的影响存在着不均匀性,本文介绍一种用于控制输入/输出比率的数据依赖门(data-dependent gate)。这种门控机制是通过对每个节点进行额外的门运算来实现的。道路图的卷积层用于对地图中的信息进行控制。 具体来说, 对于定义的图卷积,是由具有的两个参数来驱动,在图4中,是的信号,定义为:
。 (8)
。 (9)
= 1,2,..., , =1,2,..., = 1,2,..., ,这样,最后得到的道路图的卷积层如下。
(10)
若和的尺寸不同,则应使用空白张量,或首先进行线性转换。这样,路径图的卷积层就用 HW来表示。
(11)
上述方法是建立在图卷积网络基础上的道路网络相依性模型。图4中使用的某些符号说明。在图卷积网络中,对道路网的空间相关性进行了详细的描述,并给出了算法。(见图4)
1.3 路网交通流的时间依赖建模
利用图神经网络进行数据流处理,并将其嵌入到具有高阶特性的传感网络中。在此基础上,将网络引入一种基于周期神经网络的方法,得到了交通流的时效性。图5是GRU这个部分的基础架构。
该部分采用了一个基于循环神经网络的GRU,在该方法中,当前结点的输入信号是,而之前结点的隐含状态则表示为,那么门控递归单元GRU 通过和可以得到两种门控制,下述即为重置门和更新门的公式。
(12)
(13)
在图卷积网络中,是一个权矩阵,它是需要经过训练的。在获取了门控信号之后,利用重置门来获取重新设置的数据,再将'与x(t)进行拼合,然后用激活函数,把数据压缩到-1~1之间,即h'。
(14)
表示矩阵的各元素的乘积。此处h'的主要内容是由目前的输入构成的数据,加上h'到目前的隐藏状态,就等于“记住目前的状态”。更新的最后阶段使用之前获得的更新门来同时遗忘和记忆,更新的公式如下。
(15)
和代表 GRU的重置门和更新门,h'代表时间的网络输出。每一个GRU的输入都包括上一个GRU的输出,因此可以捕捉到网络的时间序列。
在 GRU单元构建完毕后,将其作为一个基础单元,用于生成最后的预测。具体来说就是在编码和译码器中,每个编码器和译码器都由两层由64个GUR组成的神经网络所组成的。用来表示地表观察,预测用来表示。
在交通流量预测模型中,输入顺序是,编码器产生一个隐藏的变量,然后用译码器对进行译码。本文对未来15分钟、30分钟、60分钟的流量状态进行了探讨,并利用预报结果和实际数据进行了损失计算,并利用训练使损失减至最小。
根据时间与空间特征的交通流量预测模型,见图7。
该章节利用图神经网络对交通流量进行空间提取,并将其嵌入到一个高维网格中,并将其嵌入到循环神经网络中。再利用序列到序列模式(seq2seq)进行预测。见图6。
2 实验环境与参数配置
2.1 交通数据集
本文以两个真实场景中的交通流为例,进行了一系列的实验。因为深度学习需要大量的数据,所以在这篇论文中,也使用了前人的研究成果。表1中所列的资料的统计结果如下。
Flow1: 洛杉矶的METR-LA流量资料。为洛杉矶的一条高速公路上的传感器所采集到的交通信息。采集时间为2012年3月1日到2012年3月7日,每个传感器的数据节点之间的时间间隔为5分钟。
Flow2: 深圳罗湖地区SZ-taxi交通资料。是深圳罗湖156条主要道路上出租车运行的数据。采集时间为2015年1月1日到1月31日,每个数据节点之间的间隔为15分钟。
2.2 数据集处理
本实验使用标准归一化方法,在不改变原始数据分布的情况下,将数据变成均值为0,标准差为1的分布。图8为对数据集进行归一化处理前后部分数据绘图所得,可以看到通过归一化处理,数据集数据在不改变其分布的情况下,使数据发生改变。
在对两个样本进行归一化后,将两个样本进行相同的分割,其中80%是训练集,20%是测试集。接着,生成训练集、测试集和校验集(Seq2seq模式),该模式是产生与特定的输入信号周期相对应的真实标志,从而为今后的建模训练做好准备。
2.3 实验配置
2.3.1 参数设置
本文的交通流量预测模型涉及以下关键参数。
学习率:在机器学习和统计领域中,学习率是优化过程中的重要参数,可以调节模型学习速度,通常设置在0.01至0.001之间,本实验中学习率设定为0.01。
循环次数:为了训练循环神经网络以获得准确的预测结果,本实验进行了多次循环,由于受到实验环境的限制,本实验设置了200次的循环。
隐藏层单元数:随着隐藏层单元数的增加,模型总体误差通常会减小,但同时也会增加网络复杂性和训练时间,可能导致过度拟合。本实验研究了分别设置为32、64和128的不同隐藏层单元数情况。
输入时间和预测时间:输入时间和预测时间是根据原始数据集中不同节点流量之间的时间间隔确定的。本实验中,输入和预测时间相同,为2小时。
数据划分:本实验将数据划分为训练集合和测试集合,采用了80%的数据作为训练集合,20%的数据用于测试。
每次处理样本数:这个参数表示每次训练时处理的样本数量,它的大小会影响训练速度。在本实验中,每次处理64个样本,这有助于加快训练速度。
2.3.2 常用交通预测指标介绍
假设为地表实际观察值,为预测值,-为观察样点的指数,本试验模式使用下列交通预报指标。
2.3.2.1 平均绝对误差(MAE)
(16)
2.3.2.2 均方根误差(RMSE)
(17)
2.3.3 对比方法
本文主要研究了基于传统机器学习和深度学习的两种方法。
ARIMA[9]:即自回归平均滑动法。通过参数模式拟合所观察到的时序。
HA:历史均值法。以历史流量资料为输入,对将来的流量进行预测。
LSTM[10]:长短时记忆网络。LSTM是一种RNN模型,由遗忘门、输入门和输出门组成。
2.3.4 环境设置
本文的交通流量预测实验是通过使用Python语言和tensorflow深度学习框架来实现。
3 实验结果分析
3.1 隐藏层单元数不同时的讨论
本节讨论隐藏层单元数对实验结果的影响。实验设置输入时间为2h,输出时间为各数据集单位时间,即数据集1的输出时间为5min,数据集2的输出时间为15min。
图9为表2、3中实验数据的对比图。可以观察到,在一定范围内,实验误差随隐藏层单元数增大而减小,实验精度随隐藏层单元数增大而增加。但超过该范围时,可能出现“过拟合”的情况,导致测试集上的训练效果不好。所以,在进行实验时,需要确定好隐藏层单元数。
3.2 算法结果对比
本节在不同预测时间下对比各算法的结果,将GCN-GRU模型在上述两个数据集中进行训练,并与三个基准方法作对比。
本节实验中参数设置为:学习率0.01,循环次数200次,输入时间2h,隐藏层单元数32,数据80%用作训练,20%用作测试。
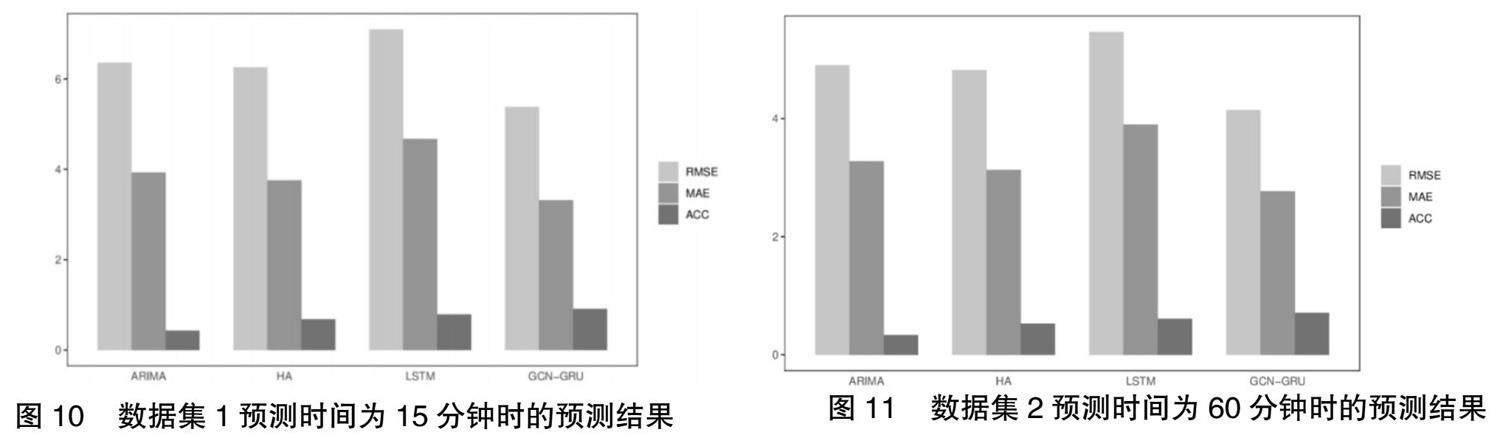
实验数据见表4、表5,从表中可以看出,传统的预测模型因其本身建模能力的局限性而使其预测效果与真实值不一致,在GCN-GRU模型中,参数RMSE、MAE对比实验中其他三个模型数值更低,精度有明显提高。
图10、11为上述表格中部分数据的对比图,可以帮助我们更直观地对比实验结果。
4 实验结论
本文主要研究了一种利用图神经网络进行交通流量预测的新方法。现实环境下的路网交通流量是空间和时间的重要特征,本研究将交通流量与空间相关性相结合,并将其与时间相关的研究成果进行了归纳。
本文比较系统地研究了国内外的交通流量预报方法。
采用图神经网络建立了基于空间相关性的道路网络交通流量模型。采用图卷积网络进行道路网络的形态学描述,通过卷积运算获取道路的空间特性;本文提出了一种利用循环神经网络捕获道路网络交通流时间依赖的模型。
利用序列-序列模型,Seq2Seq产生预测结果。在此基础上,提出了一种基于自编码器的算法,以减少模型的复杂性,提高了训练效率。
本文对METR-LA交通数据集以及深圳罗湖区交通数据集两个实际数据进行了大量的试验,提出了两个常用的交通流量预测评价指标——MAE和 RMSE。实验表明,与其他方法比较,该模型具有较好的预测性能。
参考文献:
[1] CASCETTA E.Transportation systems engineering:Theory and methods[M].New York:Springer,2001.
[2] LIU Wei,ZHENG Yu,CHAWLA S,et al.Discovering spatio-temporal causal interactions m traffic data streams[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,San Diego,California,August 21- 24,2011,New York:Association for Comouting Machinery,2011:1010-1018.
[3] LIPPI M,BERTINI M.FRASCONI P.Short-term traffic flow forecasting: An experimental comparison of time-series analysis and supervised learning[J].IEEE Transactions on Intelligent Transportation Systems,2013,14(2):871-882.
[4] VLAHOGIANNI E I.Computational intelligence and optimization for transportation big data: Challenges and opportunities[C]//LAGAROS N, PAPADRAKAKIS M.Engineering and Applied Sciences Optimization.Computational Methods in Applied Sciences,Springer,Cham, 2015,38:107-128.
[5] YU Hisang-fu,RAO N,DHILLON I S.Temporal regularized matrix factorization for high-dimensional time series prediction[C]// Proceedings of the 30th International Conference on Neural Information Processing Systems,Barcelona,December,2016,New York:Red Hook:Curran Associates Inc.,2016:847-855.
[6] LAPTEV N,YOSINSKI J,LI L E,et al.Time-series extreme event forecasting with neural networks at uber[J].International Conference on Machine Learning,2017,34:1-5.
[7] DEFFERRARD M,BRESSON X,VANDERGHEYNST P.Convolutional neural networks on graphs with fast localized spectral filtering[C]// Proceedings of the 30th International Conference on Neural Information Processing Systems,Barcelona, December,2016, New York: Red Hook: Curran Associates Inc.,2016:3844-3852.
[8] SHUMAN D,NARANG S K,FROSSARD P,et al.The emerging field of signal processing on graphs: Extending high- dimensional data analysis to networks and other irregular domams[J].IEEE Signal Processing Magazine,2013,30:83-98.
[9] MAKRIDAKIS S,HIBON M.Arma models and the box-jenkins methodology [J].Journal of Forecasting,1997,16(3):147-163.
[10] SUTSKEVER I,VINYALS O,LE Q V.Sequence to sequence learning with neural networks[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems,Montreal,Semptember,2014,Cambridge: MIT Press,2014,2:3014-3112.

