基于模型的电推进系统故障诊断方法研究

李劲泽 牛伟 王颖 张文豪

摘要：针对电动无人飞行器（EUAS）的电子传动系统，本文采用了故障模式、影响和危害性分析（FMECA）与定性贝叶斯分析（QBA）相结合的方法。该方法可以对EUAS推进系统中的关键组件和参数进行识别，并根据识别结果建立一套基于模型的分布式故障诊断架构。通过这种故障诊断方法，人们能够在有限的数据下完成复杂系统的诊断，从而克服了传统故障诊断方法需要从退化组件收集大量服役数据和性能数据的难点。

关键词：电动无人飞行器；FMECA；定性贝叶斯；故障诊断

一、引言

随着电池技术的加速改进，电动无人飞行器被越来越多地用于物流运送和医疗救援等高价值业务上。这些无人飞行器通常是完全或半自主的，自主性的加入对飞行器的安全性提出了更高要求，即电动无人飞行系统（EUAS）应能够对其当前的健康状况作出准确估计。而飞行器的电力推进系统是EUAS的关键系统[1]，持续监测和更新关键系统的健康状态，对保证EUAS安全高效运行至关重要。

电动旋翼飞行器的电推进系统基本部件包括关键的电气部件（如电池、电机等）和功率电子器件（如电子速度控制器和飞行控制系统等）。在全电动无人机Edge 540T[2]测试飞行中，发现电池出现异常大电流。经过飞行数据分析和故障排除，证实该飞行器的一个电子速度控制器（ESC）已经老化和退化，导致该EUAS操作性能下降。研究人员针对该型无人机的电力系统进行FMECA分析，利用分析结果制定了健康监测方案。但早期研究工作[1，3]集中在单个系统和组件的诊断和预测，为了实现诊断和预测功能，学者们研究了组件级退化对整个系统的影响[4-5]。他们通过开发各组件模型并进行集成，来研究和识别组件退化对级联动力传动系统的影响。例如，Hogge等[2]人利用该方法研究了EUAS中机载电池的剩余使用寿命预测，并证明了组件模型集成的可行性。

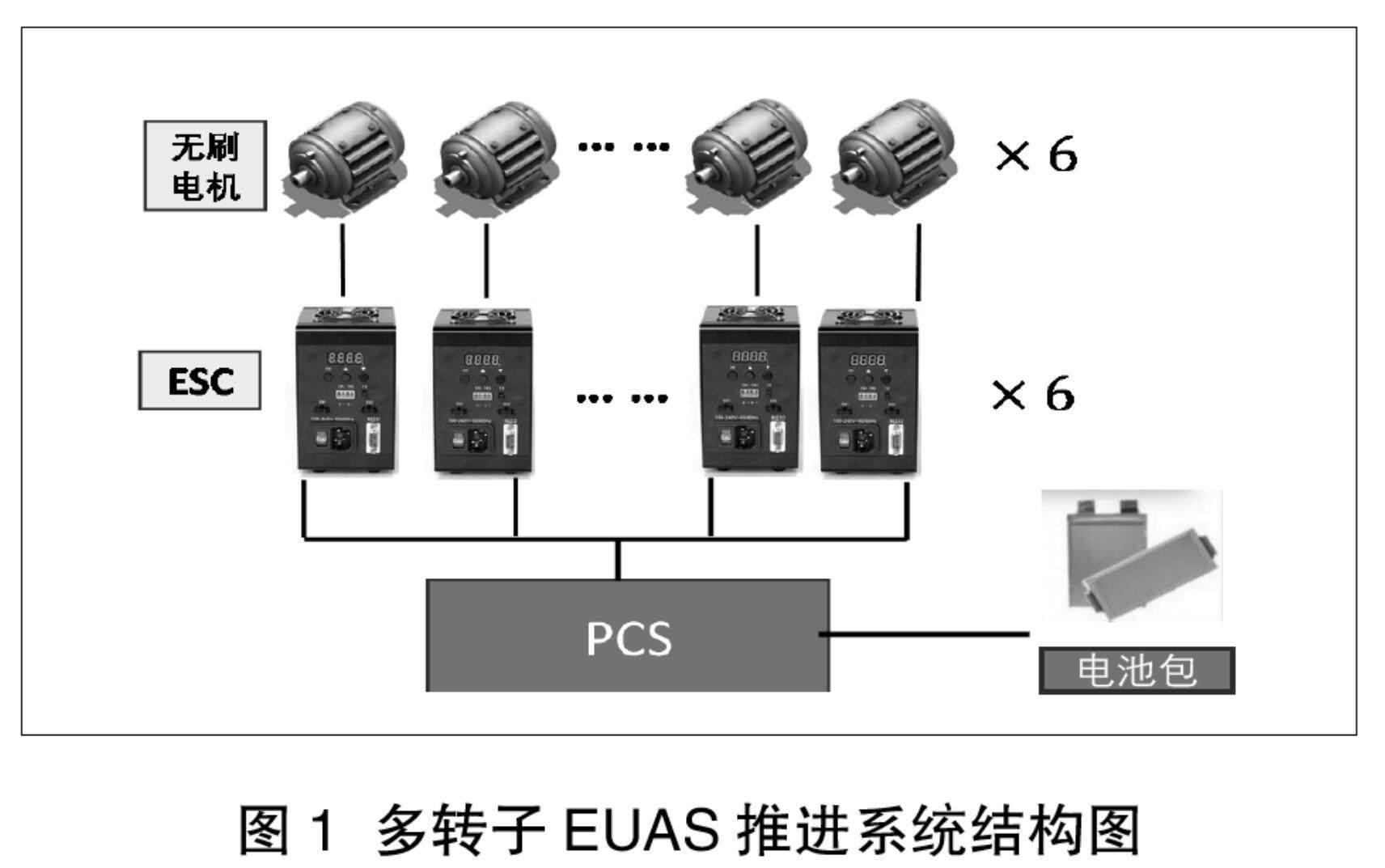
本文针对六旋翼EUAS的电推进系统展开研究，采用FMECA和定性贝叶斯分析QBA相结合的方法，以提升对关键子系统、组件和参数的识别能力。同时，将分布式故障诊断与健康管理相结合，以提高故障诊断效率，减少对机载计算机资源的需求。该EUAS动力传动系统架构示意如图1所示，系统由六个电机（M1～M6）组成，它们由六个电子速度控制器（ESC）控制，所有的电机控制器都由电源控制器系统（PCS）控制。

二、FMECA和定性贝叶斯分析（QBA）

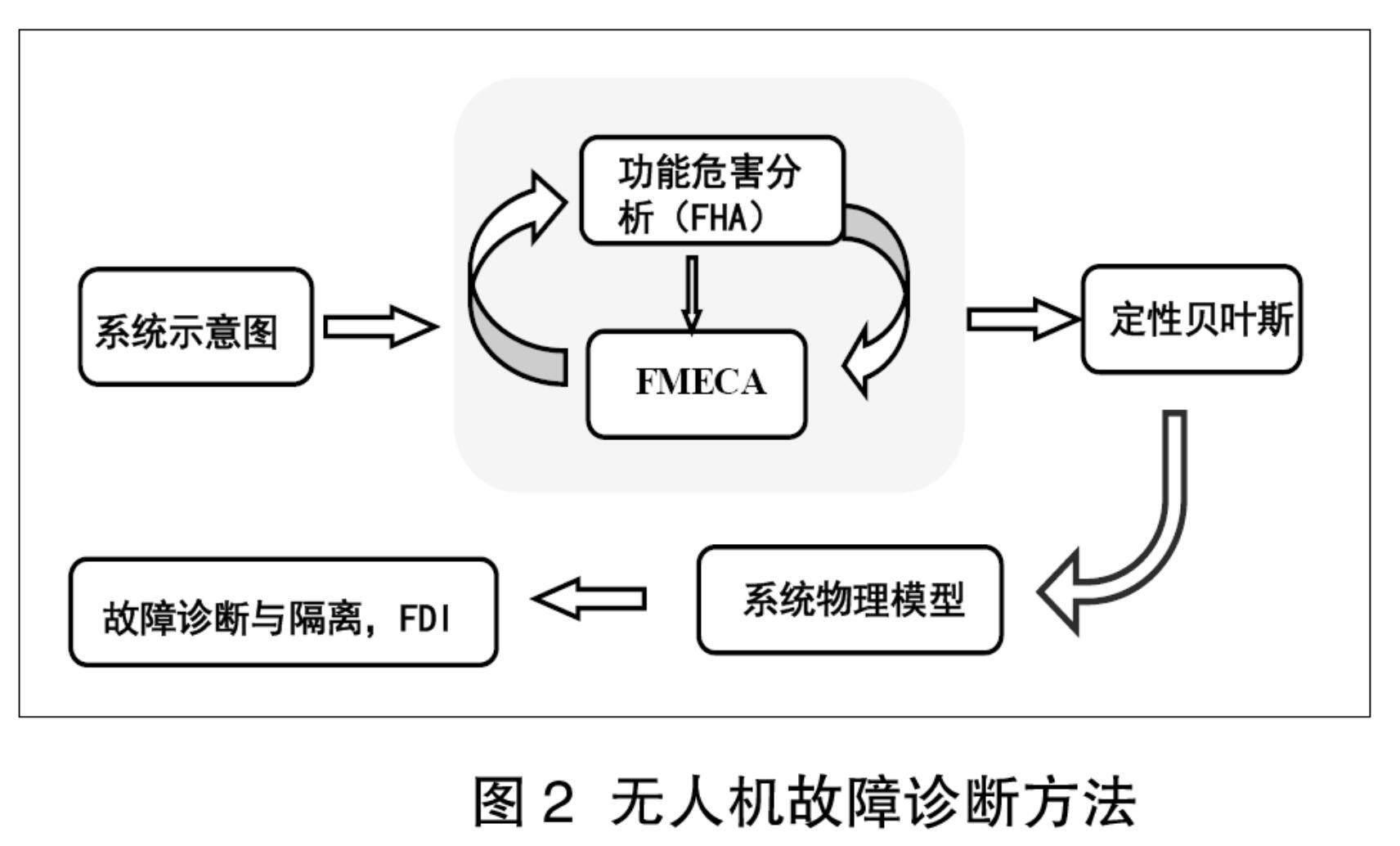
故障诊断的分析流程如图2所示。对给定系统进行功能危害性评估（FHA）是评估系统中故障风险的第一步，从功能危害性评估的输出结果能够获得对不同类型危险及其发生概率的评估。

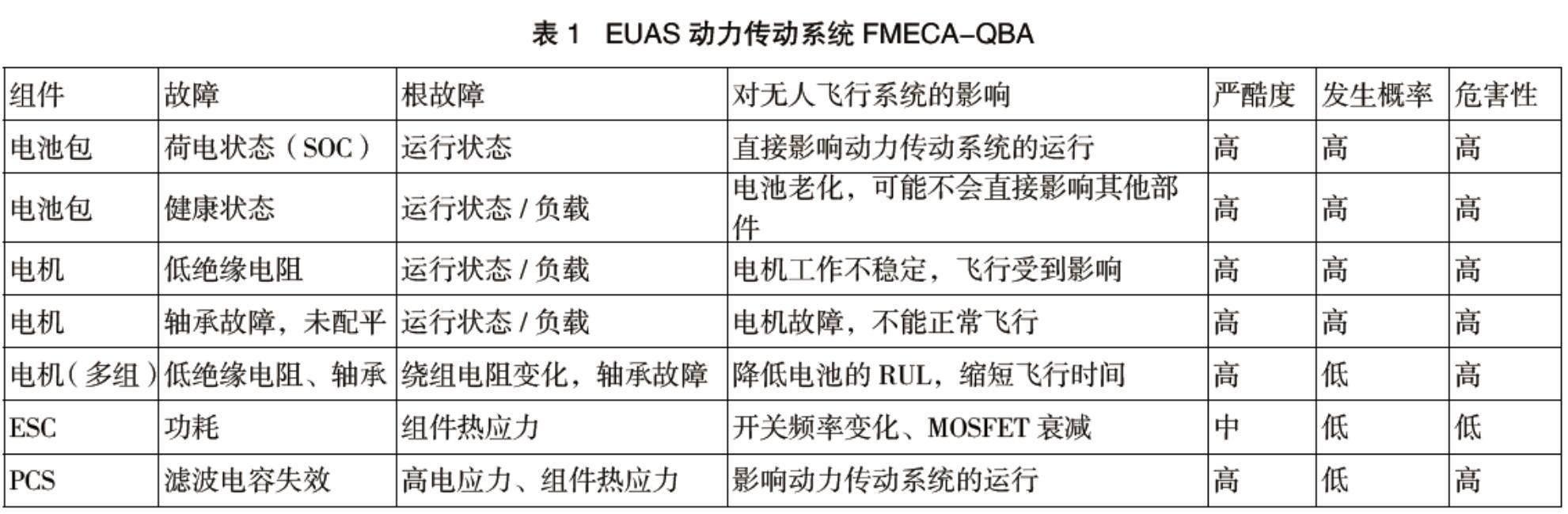
贝叶斯定理可以用定量和定性两种方法来实现[6]，贝叶斯定理的应用前提是掌握电机控制知识和系统故障的先验概率。EUAS系统的已知故障概率如表1所示，定性分析结果可分类表示为低（＜10%）、中（10%～66%）、高（67%～90%）或极高（＞90%）。

从表1中可以看出，荷电状态（SOC）有很高的故障概率，那么当电压下降时观察到故障，则认为该故障就是SOC故障。如果某故障概率属于中级，则需要进一步采用FMECA-QBA架构进行分析，并按照故障诊断架构去检测。检测到故障并完成故障隔离后，还可以按照SOC阈值预测剩余使用寿命（RUL）。

二、电动推进系统建模

参照图2讨论的无人机故障诊断步骤进行模型的联合计算，以此建立一个基于模型的故障检测和诊断总体框架。为了实现多组件联合仿真，需要建立电推进系统的模型。在完成子系统和组件识别后，根据故障概率进行排序，并根据顺序对子系统进行模型开发。本节参考表1顺序分别为电池、ESC、无刷直流电机（BLDC）开发了单独的子系统模型，并将各子系统模型连接起来，形成整个电推进系统模型，最后在MATLAB中进行仿真。

（一）电池模型

采用状态向量对电池进行描述，对电池放电结束（EOD）时电池的状态向量定义如下：

（1）

式中：qs，p、qb，p、qb，n、qs，n、V'o、V'η，p、V'η，n分别为正极表面电荷、正极体电荷、负极体电荷、负极表面电荷、电解质欧姆电阻、正极表面过电位向量、负极表面过电位向量。

这些变量的表达式和参数值在Daigle等人[7]的研究中已经详细给出，本文不再赘述。

（二）电子速度控制系统（ESC）模型

在本文中，为了方便计算，将ESC建模为一个理想的功率逆变器，它可以对三相电流进行正弦脉宽调制（SPWM）。其中，代表ESC电流换向功能的转换函数块中含有功率开关器件的理想模型，因此可以研究开关故障（开路故障和短路故障）和开关频率故障（如穿透故障）。

ESC模型运行环境如图3所示，从图中可以看出，ESC模型的输入包含了电池电压输入V、用于控制频率的脉宽调制（PWM）输入（经过桥接驱动器）和开关晶体管组成的半导体换相电路输入。F1、F2和F3是来自控制模块的PWM信号，乘以输入电压V，这样能够放大驱动三相逆变器的PWM信号[4]。该模型的输出是三相电压Va、Vb和Vc，与MATLAB提供的星型电机函数块方程（2）联立，可求得各相之间的绕组电压Vab、Vbc和Vca。

（2）

式中：V是三相电压Va、Vb和Vc的矢量表达。

（三）电机系统模型

该电机的动态模型应当描述一个三相无刷直流电机，其定子为星形绕组，转子为永磁体。该动态模型假设电子速度控制器为三相端子提供了一个给定的输入，并已知梯形波反电势，则可以将无刷直流电机表达为动力学方程形式：

（3）

式中：ωm为转子角速度；J为转动惯量；B为摩擦系数；Te为电磁转矩；Tl为负载转矩。

转子位置θm满足：

（4）

式中：p是电机极点数。

三、基于模型的分布式诊断方法

采用基于模型的故障诊断方法，通过对系统重要组成部分运行状态的监测、及时定位和隔离故障，能够保证系统持续、安全、有效地运行。大多数基于模型的诊断方案采用集中式算法，即将整个系统建为一个模型同时求解，这种方法存在固有的缺点，如计算复杂度高、单点故障难以定位和软件可伸缩性差，而分布式健康监测方法很好地解决了这些问题[8]。分布式诊断方法架构原理如图4所示，不设集中调度模块，各诊断引擎通过本地分析后，仅将部分分析结果与其他诊断引擎通信，生成全局诊断结果。

诊断引擎的设计基于文献[8提出的算法，诊断引擎同时创建一个分区结构和本地诊断器。各本地诊断器独立实现基于粒子滤波器（PF）的推理算法，用于故障检测、隔离和识别。分布式诊断方法如图5所示，每个本地诊断器执行三个主要步骤：（a）故障检测、（b）定性故障隔离和（c）定量的假设故障分解和识别。该方法将定量诊断方案与定性故障隔离方案相结合，提高了诊断效率。

当故障假设集被缩小至设定的大小k或模拟时间达到设定的时长ts时，调用故障分解与识别模块开始定量的假设故障细化和识别工作。对此时仍存在的故障假设，本地诊断引擎通过将故障参数作为随机变量引入系统标准模型（SNM）对其进行扩展，生成一个系统故障模型（SFM）。各故障模型通过粒子滤波算法跟踪观察到故障行为，并将td-Δmax时刻的估计测量值作为故障模型的输入（Δmax≥td-tf是故障发生时间tf和故障检测时间td之间可能出现的最大延迟），最后估算出子系统或部件的故障概率。

诊断引擎在训练过程中，各粒子滤波器使用Z检验来确定粒子滤波器估计的测量值与相应实际观测值的偏差是否具有统计学意义。随着观测值数量的增加，若使用的故障模型正确，则粒子滤波器在被调用时间步长sd内将收敛到观测值；若故障模型不正确，则粒子滤波器计算结果将偏离观测值。由于各故障模型都将故障概率作为随机变量包含在内，因此可以认为故障的大小（指偏离正常值百分比）就是故障模型中粒子滤波算法给出的估计值。

图6和图7展示了分布式和集中式故障诊断情况下，计算结果的收敛情况和CPU占用情况。可以发现，分布式计算能够更快地完成计算并收敛到观测值，然后完成模型的训练，且此过程中占用的计算资源更少。

四、结束语

本文对EUAS电推进系统健康监测和诊断方法进行了研究，将FMECA和定性贝叶斯分析（QBA）与基于模型的分布式故障诊断结合，形成了一种新的故障诊断架构。通过利用FMECA和QBA对组成EUAS电推进系统的子系统和组件故障概率的识别，能够使诊断程序更快识别和隔离故障系统和组件。在EUAS上应用本文提出的基于模型的分布式机载诊断架构，不仅能最大程度减少需监测的子系统和组件数量，还能够通过分布式的计算处理能力，有效降低机载计算机资源需求。

作者单位：李劲泽 牛伟 王颖 张文豪 中国航空工业集团公司西安航空计算技术研究所

参考文献

[1] 方淳，巨亚鸽，李巍，等.大型飞机电力推进系统关键技术[J].海南师范大学学报：自然科学版，2021，34（2）：195-203.

[2] Hogge E，Bole B，Vazquez S， et al.Verification of Prognostic Algorithms to Predict Remaining Flying Time for Electric Unmanned Vehicles[J].IJPHM，2018，9（1）.

[3] 王永强，律方成.基于贝叶斯网络的电容型设备故障诊断[J].电网技术，2009（17）：4.

[4] Gorospe G， Kulkarni C S， Hogge E，et al. A study of the degradation of electronic speed controllers for brushless DC motors[C]// Asia Pacific Conference of the Prognostics and Health Management Society 2017. 2017 （ARC-E-DAA-TN42858）.

[5] 徐田镇.航空发动机退化状态参数估计与控制技术研究[D].南京航空航天大学，2017.

[6] Medow， Mitchell， A， et al. A qualitative approach to Bayes theorem[J]. Evidence Based Medicine， 2011.

[7]Daigle M，Kulkarni C S.Electrochemistry-based Battery Modeling for Prognostics[J]. 2013.

[8] 张莉，袁海文.飞机电源多Agent预测与健康管理系统研究[J].计算机工程与应用，2010，46（19）：5.