新型单传感器半主动悬架控制算法机理研究

李根 邵雄 赵伟冰 谢欣秦 李闯

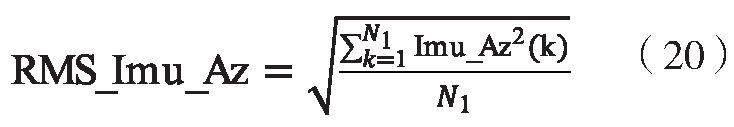
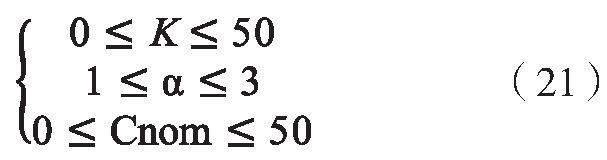
摘  要：半主动悬架控制算法研究，对提高汽车的平顺性和操纵稳定性，具有非常重要的意义。本文首先建立了一种三自由度车辆模型，并基于试验场采集的试验数据作为模型的工况输入。然后，提出了一种新型单传感器算法，并基于建立的控制算法和三自由度车辆模型闭环仿真平台，对新型单传感器算法进行了仿真分析，从理论上验证了算法的优势以及算法参数对平顺性的影响规律。最后，在闭环仿真平台中对新型单传感器算法的参数进行了优化，结果表明，相对于被动减振器，在鹅卵石路面和长波路面上，新型单传感器算法车身质心加速度RMS指数分别降低了21%和14%，大幅提升了车辆的舒适性。

关键词：半主动减振器；车辆模型；新型单传感器算法；仿真分析；参数优化

中图分类号：U463.33     文献标志码：A      文章编号：1005-2550（2024）03-0002-08

Research and Application of a Novel Single Sensor Semi-Active Suspension Control Algorithm

Abstract： The research on the control algorithm of semi-active suspension is of great significance to improve the comfort and handling stability of automobiles. Firstly， the three degree of freedom vehicle model is established in this paper， and experimental data obtained from the proving ground is used as input for the simulation conditions of the model. Then， a novel single sensor algorithm is proposed， and based on the established control algorithm and a closed-loop simulation platform of a three degree of freedom vehicle model， simulation analysis is conducted on the novel single sensor algorithm. The advantages of the algorithm and the impact of algorithm parameters on ride comfort were theoretically verified. Finally， the parameters of the novel single sensor algorithm is optimized on the closed-loop simulation platform， and the results showed that compared to the passive shock absorber， the RMS index of the vehicle centroid acceleration of the novel single sensor algorithm decreased by 21% and 14% respectively on pebble and long wave road of proving ground， significantly improving the comfort of the vehicle.

Key Words： Semi-Active Shock Absorber; Vehicle Model; Novel Single Sensor Algorithm; Simulation Analysis; Parameter Optimization

1    前言

隨着生活水平的提高以及新能源汽车的迅猛发展，人们对汽车驾驶体验的要求也越来越高。车辆乘坐舒适性和操纵稳定性作为直接影响乘员感官体验和人身安全的特性，得到了越来越多的关注。车辆悬架连接车轮与车身，起到隔振及传力作用，是决定车辆动力学性能的重要系统之一[1]。对于传统的被动减振器而言，若想减小车身的振动，则需要较软的减振器来过滤路面的起伏，即舒适性较好；若想保证汽车在制动、加速、转弯时车身姿态的稳定，则需要较硬的减振器来减小车身的俯仰和侧倾，即操纵稳定性较好。也就是说车辆乘坐舒适性和操纵稳定性之间存在冲突。而半主动减振器，可以根据路况和车辆运动信息，实时调节减振器的阻尼系数，以此适应不同的路面情况，使车辆始终在最佳状态下运行，进而解决操纵稳定性和平顺性之间存在的矛盾[2，3]。

目前半主动悬架垂向控制算法，主要是天棚控制算法和开关型单传感器控制算法。天棚控制算法主要包括速度天棚[4]、加速度天棚[5]和混合天棚[6]，对于4轮汽车，天棚算法一般至少需要4个簧上加速度传感器和4个悬架位移传感器（或者4个簧下加速度传感器），这导致系统结构复杂和成本大幅增加，不利于大规模商业化应用；开关型单传感器控制算法[7]，一般需要4个簧上加速度传感器，也会增加一定的成本以及占用车辆布置空间，同时，传统单传感器控制算法，阻尼在最大和最小之间切换，会引起异常颤振，降低车辆的平顺性。

本文提出了一种新型单传感器算法，该算法来源于作者团队的发明专利[8]，算法只需要一个IMU惯性测量单元传感器，且IMU嵌入在控制器硬件中，系统简单，成本低。然后，本文基于所建立的控制算法和三自由度车辆模型闭环仿真平台，对新型单传感器算法进行了仿真分析，从理论上验证了算法的优势以及算法参数对平顺性的影响规律。最后，在闭环仿真平台中对新型单传感器算法的参数进行了优化，验证了优化后的算法参数对车辆平顺性的改善作用。

2    車辆模型和仿真工况的建立

目前车辆动力学仿真软件主要有Carsim和Adams等，建模思路是根据车辆参数和试验场采集的数字路面，建立车辆仿真模型和路面模型，但该模型需要有精确的路面三维信息和轮胎动力学数据以及两者之间的耦合关系，而这些数据一般不易获取，建模成本高。同时，控制算法一般在Matlab/Simulink软件中建立，为了与车辆模型进行闭环仿真，需要与Carsim或者Adams联合，增加了仿真的复杂度。

本文提出了一种三自由度车辆模型，主要包括车身质心垂向运动自由度、俯仰自由度和侧倾自由度，该模型可以反映车辆大部分的平顺性和操纵稳定性，同时该模型可以避开轮胎和路面的建模难度，将复杂问题简单化，并且可以最大限度再现试验场工况。具体建模思路如下。

首先根据车辆动力学原理以及基本的车辆参数，利用Matlab/Simulink软件建立三自由度车辆模型；然后根据实车采集的车轮垂向加速度作为模型的平顺性仿真输入，根据实车采集的加速和制动工况时的车身纵向加速度信号和转向工况时车身侧向加速度信号作为模型操稳性仿真输入。

2.1   三自由度车辆模型建立

图1为整车三自由度垂向动力学模型。车身17的质心包含垂向运动位移Zc、俯仰运动角度φ和侧倾运动角度θ这三个自由度。车辆模型前进方向为x轴正方向，垂直向上为Z轴正方向，然后根据右手定则确定y轴的正方向，侧倾角和俯仰角的正方向根据右手定则确定。车身质量为Ms，俯仰转动惯量为Iy，侧倾转动惯量为Ix。左前悬架弹簧的刚度为KFL，左前半主动减振器的阻尼为CFL；左前车轮轮心1在车身7上的投影点为左前簧上点13。右前悬架弹簧6的刚度为KFR，右前半主动减振器10的阻尼为CFR；右前车轮2在车身17上的投影点为右前簧上点14。前横向稳定杆18的侧倾角刚度为KFroll。左后悬架弹簧7的刚度为KRL，左后半主动减振器11的阻尼为CRL；左后车轮3在车身17上的投影点为左后簧上点15。右后悬架弹簧8的刚度为KRR，右后半主动减振器12的阻尼为CRR；右后车轮4在车身17上的投影点为右后簧上点16。后横向稳定杆19的侧倾角刚度为KRroll。车身17质心到左前簧上点13和右前簧上点14连线的垂直距离为a；车身17质心到左后簧上点15和右后簧上点16连线的垂直距离为b；左前簧上点13和右前簧上点14的距离为Bf，左后簧上点15和右后簧上点16的距离为Br。左前簧上点13的垂向位移为ZsFL，右前簧上点14的垂向位移为ZsFR，左后簧上点15的垂向位移为ZsRL，右后簧上点16的垂向位移为ZsRR。左前车轮1的垂向位移为ZuFL，右前车轮2的垂向位移为ZuFR，左后车轮3的垂向位移为ZuRL，右后车轮4的垂向位移为ZuRR。

根据车辆动力学理论，三自由度车辆动力学模型建立过程如下。

簧上4角垂向位移的表达式如式（1）：

各悬架所受到的弹簧力和阻尼力合力Fi的表达式如式（2）：

式（2）中，λi为悬架的杠杆比，i=[FL， FR， RL， RR]，FL代表左前，FR代表右前，RL代表左后，RR代表右后。

前悬架和后悬架横向稳定杆提供的抗侧倾力矩分别为MFθ和MRθ，计算公式如式（3）和式（4）：

三自由车辆模型的动力学方程如式（5）、（6）、（7）：

式（6）、（7）中，Mx为由于转向引起的侧倾力矩，My为由于制动和加速引起的俯仰力矩。

2.2   仿真输入工况的建立

根据车辆质心处的纵向加速度Ax，如图2（b）（c）所示，计算由于制动和加速引起的车身质心的俯仰力矩My，并作为模型的操稳仿真输入。计算公式如式（9）。

式（9）中，hx为车辆的纵倾力臂。

根据车辆质心处的侧向加速度Ay，如图2（d）所示，计算由于转向引起的车身质心的侧倾力矩Mx，并作为模型的操稳仿真输入。计算公式如式（10）。

（10）

式（10）中，hy为车辆的侧倾力臂。

3    新型单传感器算法

本文提出的新型单传感器算法来源于作者团队的发明专利[8]，该算法主要包括平顺性控制模块、抗俯仰控制模块、抗制动俯仰控制模块、抗加速俯仰控制模块和抗转弯侧倾控制模块，可以使车辆达到最佳的平顺性和操纵稳定性。

车身抗俯仰控制算法、抗制动点头控制算法、抗加速抬头控制算法以及抗转向侧倾控制算

传统的开关型单传感器控制算法[7]表达式如式（11）下。

将式（12）进行线性化处理，新型单传感器算法计算的阻尼Cni如式（13）。

式（13）中，Cri为当量阻尼，表达式如式（14）。

Cri=ki·F1i·F2i+ Cnomi，且0 ≤Ci≤ 100  （14）

4    新型单传感器算法仿真分析

4.1   仿真平台的建立

为了对新型单传感器算法进行仿真分析，需要建立控制算法与车辆模型闭环仿真平台。

图3为在Simulink软件中建立的半主动悬架控制算法与车辆模型仿真平台框图，主要包括工况输入、3自由度车辆模型和新型单传感器算法。首先将路面激励输入给车辆模型，然后车辆模型将质心IMU信号输入给单传感器半主动悬架控制算法模块，最后新型单传感器算法模块输出控制阻尼给车辆模型，改善车辆的平顺性和操稳性。

4.2   新型单传感器算法原理分析

基于建立的控制算法与车辆模型仿真平台，对新型单传感器算法的原理进行仿真分析，并和传统开关型单传感器算法进行对比，验证新型单传感器算法的优点。

图4为传统的开关型单传感器算法当量阻尼图，当F1i和F2i的乘积符号变化时，当量阻尼Cri在最大和最小值之间切换，阻尼变换比较突兀。

图5为新型单传感器算法当量阻尼图，当F1i和F2i的乘积符号变化时，新型单传感器算法的当量阻尼Cri切换平滑。

图6为不同算法质心垂向加速度幅频特性对比，相比于最大阻尼和最小阻尼条件，新型单传感器算法能够同时降低低频和中高频的振动幅值，提高平顺性。相比于传统开关型单传感器算法，新型单传感器算法降低了中高频的振动幅值，提高平顺性。

图7为不同算法质心垂向加速度对比，新型单传感器算法质心垂向加速度变化比较平滑，而传统的开关型单传感器算法存在加速度震颤现象，降低了平顺性。

4.3   新型单传感器算法参数影响因素分析

基于建立的控制算法与车辆模型仿真平台，对新型单传感器算法的不同参数进行影响因素仿真分析，研究新型单传感器算法参数对车辆平顺性的影响规律。

4.3.1 参数K影响因素分析

图8为不同参数K下质心垂向加速度幅频特性对比。K增大，车辆质心处垂向加速度一阶共振峰值减小，减小了低频时车身的垂向运动。但是K太大的话，过小的一阶垂向运动，会让驾驶员感觉低频时车体运动太小，缺乏柔和感。K增大，二阶共振幅值基本不变，对中高频的舒适性影响不大。

选择不同的K，可以带来不同的低频控制效果，进而可以带来不同的驾驶感受，比如舒适、正常和运动模式。

4.3.2 参数α影响因素分析

圖9为不同参数α下质心垂向加速度幅频特性对比。α增大，车辆质心处垂向加速度的一阶共振峰值减小，减小了低频时车身的垂向运动。但是α太大的话，过小的垂向运动，会让驾驶员感觉低频时车体运动太小，缺乏柔和感。α增大，二阶共振幅值基本不变，对中高频的舒适性影响不大。

4.3.3 参数Cnom的影响因素分析

图10为不同参数Cnom下质心垂向加速度幅频特性对比。Cnom增大，车辆质心处垂向加速度的一阶共振峰值减小，减小低频时车身的垂向运动。

Cnom增大，车辆质心处垂向加速度的二阶共振峰值增大，对中高频垂向振动的抑制效果不好，过大的话，会让起驾驶员感觉中高频抖动增多。

5    新型单传感器算法参数优化

基于建立的控制算法与车辆模型仿真平台，对新型单传感器算法参数进行优化，提高车辆的平顺性。

将采集的试验场平顺性路面簧下加速度数据作为闭环仿真模型的路面输入，以质心垂向加速度均方根值RMS_Imu_Az最小化作为优化的目标函数，对参数K、参数α和参数Cnom进行迭代优化。

目标函数：

式（20）中，k为某一采样点，N1为试验场平顺性路面的总采样点数，Imu_Az （k）为某一采样点下质心垂向加速度。

约束条件：

使用Matlab软件中的fmincon函数，对以上模型进行最优参数α迭代求解，优化后的算法参数结果为：K=9.5，α=1.9，Cnom=11。

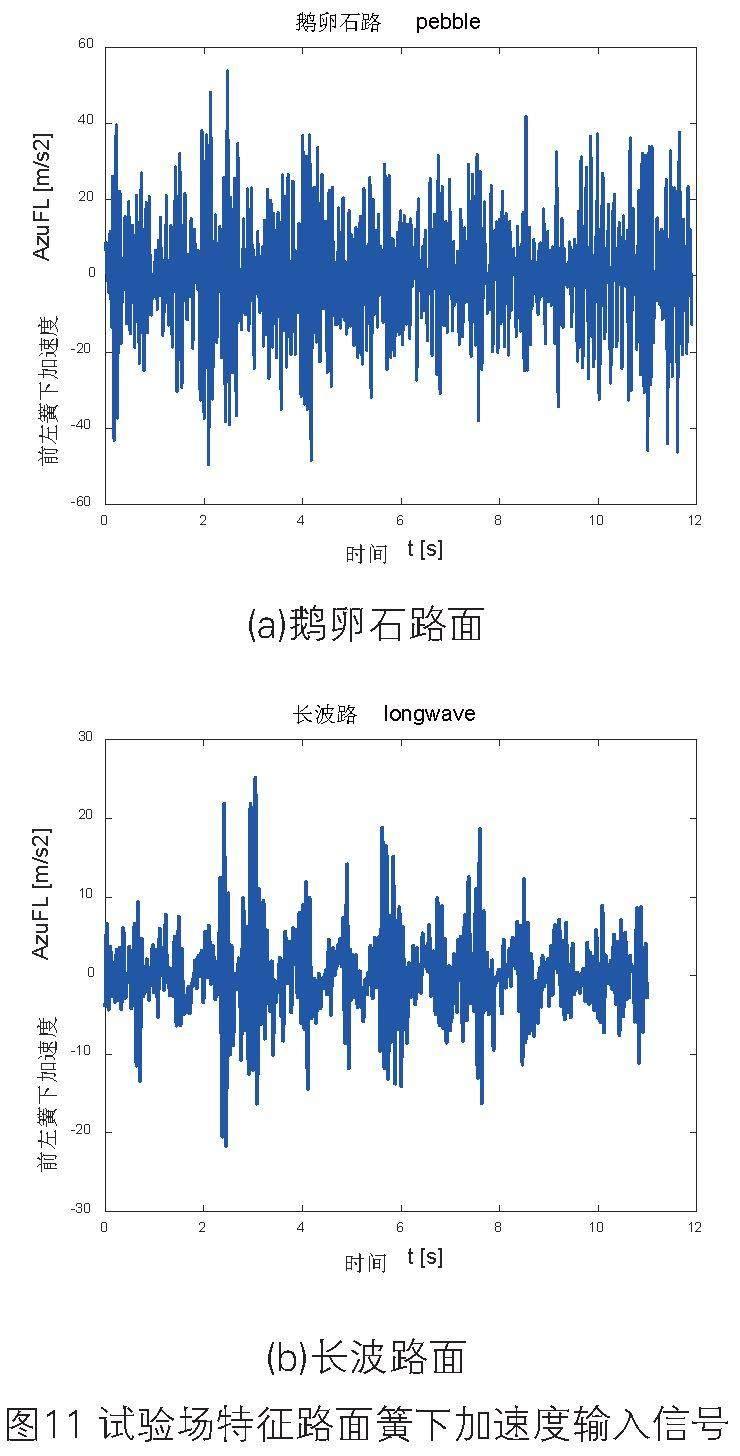
选择典型特征路面，对优化后的算法控制效果进行仿真对比。仿真工况为，鹅卵石路输入（图11a）和长波路输入（图11b），分别在最小阻尼、最大阻尼，原车被动减振器和新型单传感器算法方案下，记录不同方案的车辆质心垂向加速度Imu_Az，通过加速度均方根值指数Imu_Az_RMS_Index，来评价算法对平顺性的改善效果。

加速度均方根值指数Imu_Az_RMS_Index定义为式（22）。

式（22）中，j=1，2，3，4，j=1代表最小阻尼条件，j=2代表最大阻尼条件，j=3代表原车被动减振器条件，j=4代表新型单传感器算法条件。RMSj的计算公式如式（23）。

式（23）中，k为某一采样点，N2为鹅卵石路面或者长波路面的总采样点数。

仿真结果如图12所示，结果表明，相对于被动减振器，在鹅卵石路面和长波路面上，新型单传感器算法质心加速度均方根值指数分别降低了21%和14%，大幅提升了车辆的平顺性。

6    结束语

本文提出了一种新型单传感器算法，并建立了控制算法和车辆模型闭环仿真平台；然后通过仿真分析，从理论上验证了算法的优势以及算法参数对平顺性的影响规律；最后，在闭环仿真平台中对新型单传感器算法的参数进行了优化，验证了优化后的算法参数对车辆平顺性的改善作用。

结论如下：

1）新型单传感器半主动悬架控制算法，仅需要一个IMU传感器就可以改善平顺性和操稳性，系统简单，成本低，有利于大规模应用。

2）新型单传感器算法可以提高车辆不同频率段的平顺性，验证了该算法的有效性。同时，相比于传统开关型单传感器算法，新型单传感器算法阻尼切换更加平滑。

3）通过建立的控制算法和车辆模型闭环仿真平台，研究了新型单传感器算法参数对车辆平顺性的影响，为后续实车标定调试提供理论支撑，可缩短实车调试的周期。

4）在闭环仿真平台中对新型单传感器算法的参数进行了优化，车辆在鹅卵石路面和长波路面上，相比于被动减振器，优化后的新型单传感器算法参数方案的质心加速度均方根值指数值分别降低了21%和14%，大幅提升了车辆的平顺性。

参考文献：

[1]余志生. 汽车理论[M]. 北京：机械工业出版社，2011.

[2]喻凡，林逸. 汽车系统动力学[M]. 北京： 机械工业出版社，2016.

[3]LI J， ZHANG X Y， FU L， et al. Semi-Active Suspension Control Design for Vehicles [M]. Automobile Technology， 2017（4）： 1-5.

[4]Karnopp， D.， Crosby， M.， and Harwood， R.. Vibration control using semi-activeforcegenerators[J]. Journal of Engineering for Industry. 1974，96（2）：619–626.

[5]Savaresi， S.， Siciliani， E.， and Bittanti， S. Acceleration driven damper （ADD）： an optimal control algorithm for comfort oriented semi-active suspensions [J]. ASMETransactions： Journal of Dynamic Systems， Measurements and Control. 2005， 127（2）：218–229.

[6]Savaresi， S. and Spelta， C. Mixed sky-hook and ADD： Approaching the filtering limit of a semi-active suspension[J]. ASME Transactions： Journal of Dynamic Systems， Measurement and Control， 2007， 129（4）：382–392.

[7]Savaresi， S. and Spelta， C. A single sensor control strategy for semi-active suspension[J]. IEEE Transaction on Control System Technology， 2009， 17（1）：143–152.

[8]邵雄，李根，谢欣秦，等. 半主动悬架控制方法及控制装置、存储介质及车辆[P]. CN 116021939 A，2023.