基于群体智能算法的巡飞弹向心攻击优化方法及实验分析

徐雨甜

摘要：近几年，无人机巡飞弹打击成为一种重要的作战方式。针对巡飞弹向心攻击问题，选用蝙蝠优化算法、人工蜂群算法、粒子群算法、鲸鱼优化算法，设计一种基于群体智能算法的巡飞弹向心攻击优化方法，通过实验设计和结果分析对比四种群体智能优化算法，以提高巡飞弹向心攻击的作战效率。实验验证了该方法的有效性，且结果表明人工蜂群算法和粒子群算法总体表现较优。

关键词：无人机巡飞弹；向心攻击；群体智能优化算法；粒子群优化算法；人工蜂群算法

一、前言

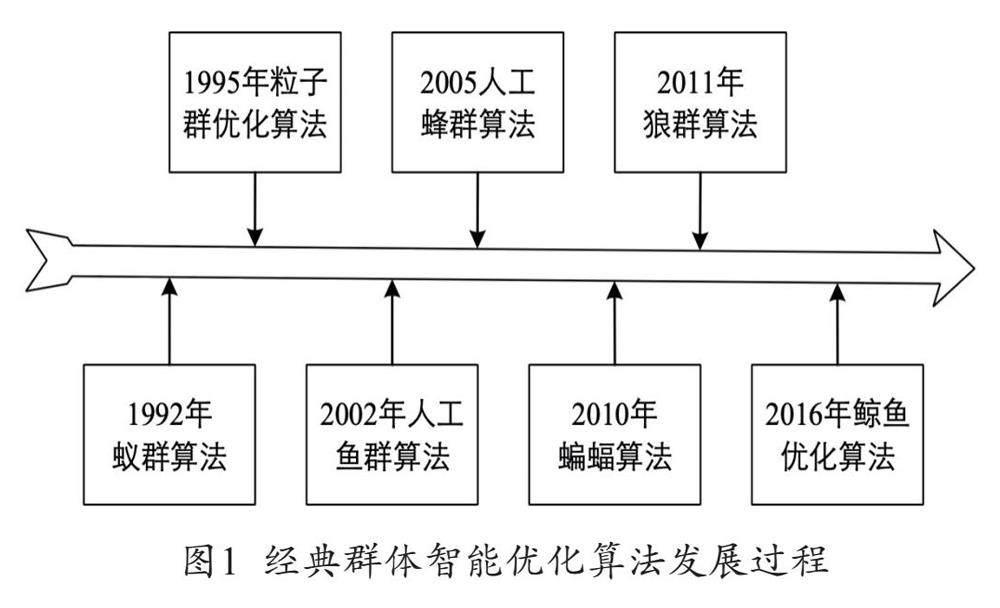
现代战争中战场环境瞬息万变，无人智能集群的自主协同作战必将成为未来战争的重要作战模式。巡飞弹作为一种先进的智能导弹，是基于无人机与巡航导弹的先进技术，具备精准打击的自主协同作战能力，成为改变传统作战模式的一种新型武器，巡飞弹的协同攻击对信息化军事战争条件下的多目标任务发挥着重要作用。目前，巡飞弹作战中存在着任务分配或路径规划不合理、攻击效果不理想等问题。为此，需要研究巡飞弹协同攻击任务分配和路径规划方法，提高作战效能。群体智能算法是一种基于生物群体行为规律的计算技术，常用来解决组合优化、路径规划等问题。1989年Beni和Wang首次提出了“群体智能”的概念。如图1为群体智能优化算法在2010年之前的发展过程[1-2]。本研究选择了比较适合巡飞弹向心攻击问题的四种群体智能优化算法进行研究分析，分别是蝙蝠算法、粒子群优化算法、鲸鱼优化算法、人工蜂群算法，并通过实验对比测试它们的优化效果。最后得出实验结论，并对巡飞弹向心攻击未来发展提出展望。本研究基于四种群体智能算法对巡飞弹向心攻击问题进行研究，设计出一种基于群体智能算法的巡飞弹向心攻击优化方法。研究工作主要包括以下几个方面：一是建立巡飞弹向心攻击问题模型，设计向心攻击路径规划算法。二是通过实验对比四种群体智能算法对于实现巡飞弹向心攻击的有效性与可行性。

二、相关算法描述

（一）蝙蝠算法

蝙蝠算法[3]（Bat Algorithm，BA）是2010年由Yang Xin-She提出的受微型蝙蝠回声定位启发的算法。在回声定位的帮助下，蝙蝠可以测量物体的大小和距离，并用于导航和觅食，蝙蝠的这一特性被用于制定出蝙蝠算法。在蝙蝠算法中，每个蝙蝠在位置 上以速度 随机飞行，当蝙蝠发现猎物时，它会改变频率 、响度和脉冲发射率来选择最优解，直到目标停止。

（二）粒子群算法

粒子群算法[4]（Particle Swarm Optimization，PSO）是1995年由Kennedy和Eberhart首次提出，算法模拟鸟群觅食行为中的相互合作机制，算法结构简单且容易实现。粒子群算法的大致流程：首先将一群粒子随机进行初始化，种群规模一般为30，然后所有的粒子根据个体极值和群体极值来更新自己的位置。

（三）鲸鱼优化算法

鲸鱼优化算法（Whale Opti-mization Algorithm，WOA）是2016年由Mirjalili[5]等人提出的新的受自然启发的优化算法。鲸鱼优化算法模拟鲸鱼的捕食行为，主要分为三类：包围猎物、发泡网攻击、搜索捕食。鲸鱼优化算法的应用有：Aziz等人提出鲸鱼优化算法和飞蛾火焰优化算法相结合用于确定图像分割的多级阈值中；Wang等人提出一种基于粗糙集的改进鲸鱼算法用于特征选择中。

（四）人工蜂群算法

人工蜂群算法（Artificial Bee Colony algorithm，ABC）是2005年由KARABOGA首次提出的蜜蜂觅食过程中各种行为的启发式优化算法。该算法模拟蜂群的分工和信息交流，相互协作完成采蜜任务的行为。ABC具有运算简单、探索能力强、参数较少等特点而被广泛研究。

三、巡飞弹向心攻击问题建模

（一）问题描述

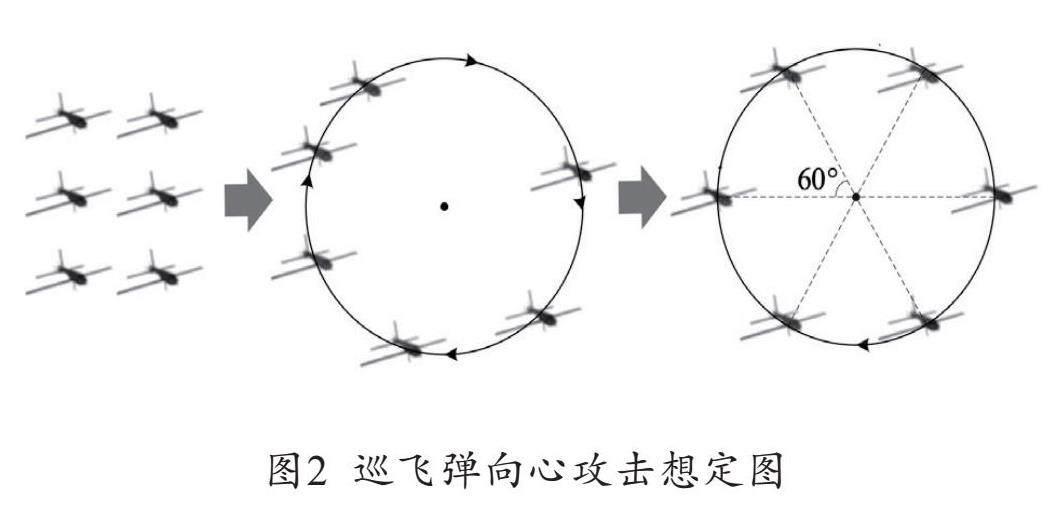
巡飞弹向心攻击流程可划分为3个阶段，第一阶段是逼近阶段，各个巡飞弹潜行到达目标位置，目标位置是以目标为圆心，向心打击距离为半径飞行的圆周。第二阶段是形成合围阶段，巡飞弹调整飞行速度和间隔距离，最终每个巡飞弹之间的距离均等且匀速飞行。第三阶段是向心打击阶段，全体巡飞弹圆心进行打击任务，并以最大速度向目标点发起自杀式攻击。例如，12个巡飞弹为一组进行向心攻击任务，在合围阶段最终形成相邻两个巡飞弹夹角为30°的合围圈，并匀速绕圈飞行。巡飞弹向心攻击想定图如图2所示。在巡飞弹向心攻击中，本算法主要实现第一阶段和第二阶段，为提高攻击效率，需要优化巡飞弹的进攻路径，即如何在最短时间到达目标位置，形成合围圈。本研究设计基于群体智能的巡飞弹向心攻击优化算法规划巡飞弹的进攻路径，考虑以在二维空间运动的巡飞弹执行向心攻击作战任务为研究背景，通过巡飞弹协同攻击过程中最大飞行距离、飞行速度、转角限制等战斗指标，建立巡飞弹向心攻击路径规划优化模型，进行巡飞弹向心攻击路径规划问题的研究。研究假设战场存在地形障碍和人工障碍，但不考虑禁飞区及地面目标对巡飞弹造成的防空威胁等，并且战场信息透明，不存在突发威胁。

（二）巡飞弹向心攻击优化模型的构建

巡飞弹向心攻击路径规划可详细描述为多枚巡飞弹，首先确定发射巡飛弹数量，接着进行打击路线路径规划。假设给定 枚巡飞弹组成巡飞弹集群LM={LM1，LM2，…，LMn}执行协同作战任务，对地面目标进行打击。构建目标函数时，应分析不同因素对路径的影响：

1.最长飞行距离

由于巡飞弹通过自身携带电池进行供能，巡飞时间有限，限制了巡飞弹的最大飞行距离，必须设定巡飞弹在失去动力前进行自毁或自失效，以保证其作战使用安全。故给定巡飞弹LMi的飞行距离为S（LMi ），设LMi的最长飞行距离为Smax，则该条件可表示为公式（1）：

S（LMi）

到达时间差。在巡飞弹集群执行向心攻击任务时，为顺利执行打击任务，要求巡飞弹到达目标位置的时间差越小越好，设巡飞弹集群的最大时间差为?tmax，即公式（2），巡飞弹到达目标位置的时间差为：

?t=max（?t1（|LM1-LM2|），?t2（|LM2-LM3|），…，

?tm（|LMn-1-LMn|））

2.安全避障

巡飞弹在潜行阶段，由于战场地形复杂，需考虑避障问题。

3.航迹转角限制

为保证巡飞弹在进攻飞行过程中转向时平缓，应预设最大转角。在飞行中，巡飞弹都应保持小于或等于最大转角，以避免出现急转弯的情况。设定水平转角代价，其值为当前转向角和预定最大转向角之间的差。α表示巡飞弹的实时水平转角，αmax为巡飞弹最大水平，即转角限制转向角限制公式如（3）所示：

Jangle（LMi ）= {       0，α≤αmax

α-αmax，α>αmax （3）

（三）基于群体智能的巡飞弹向心攻击优化算法设计

求解巡飞弹向心攻击问题时，针对问题中存在的约束条件，本文设计出一种基于群体智能算法的巡飛弹向心攻击优化算法，为巡飞弹向心攻击问题给出最佳方案，给出不同任务所需不同规模的巡飞弹集群时，选择并对比分析蝙蝠优化算法、人工蜂群算法、粒子群算法、鲸鱼优化算法的优劣，算法流程如图3所示。

四、实验与结果分析

（一）实验环境及参数设置

为给出巡飞弹向心攻击问题的最优方案，本文分别对6—30个巡飞弹组成的集群进行比较实验，四种算法实验参数的详细信息见表1。为了更有说服力，在所有情况下，对每种不同规模的巡飞弹集群进行10次独立实验，各种算法所选取的参数均为原始论文所选参数。

所有实验的集成开发环境为Matlab_R2021b，操作系统为windows_22_22H2。

（二）实验结果分析与讨论

用枚举法进行巡飞弹路径规划时，巡飞弹集群LMi为6时的适应度为42.0095，表现较好，但是集群数量 超过6时，效率变得极低且耗时很长，无法满足任务条件。

在进行的25组实验中，实验结果见表2，除去一组无效数据，共有24组有效数据。

鲸鱼优化算法LMi=10，13，17，18，27，28，30时表现最优，人工蜂群算法在LMi=6，7，8，14，15，16，19，22，28，30时表现最优，粒子群算法在LMi=9，11，12，13，20，21，23，24，26时表现最优，蝙蝠优化算法表现都不理想。

如图4所示，人工蜂群算法和粒子群算法总体表现最优，集群数量在6—16时，人工蜂群算法在四种算法中最优占比55%；集群数量在17—30时，粒子群算法在四种算法中最优占比43%，因此在巡飞弹进行规模较小的任务时，人工蜂群算法效果更好，可以优先选择；在巡飞弹进行规模较大的任务时，粒子群算法效果更好，可以优先选择。

如图5所示，粒子群优化算法的总体效果最好，人工蜂群算法的平均值（38.51）略低于粒子群优化算法（38.92）。其次是鲸鱼优化算法（39.50），此算法标准差较小，说明效果更稳定，而蝙蝠优化算法在各个方面的表现都不突出。

（三）实验结论

实验验证了该巡飞弹向心攻击方法的有效性，结果表明人工蜂群算法总体表现最优，其次是粒子群算法和鲸鱼优化算法，蝙蝠优化算法的效果最差，要结合任务的不同规模选择合适的算法。

五、结语

探讨了基于群体智能算法的巡飞弹向心攻击方法研究与分析，通过算法对比分析出四种群体智能优化算法的优劣，可以高效选择巡飞弹向心攻击的最佳路径，既分析了多个群体智能算法在解决优化问题时各自的特点，也提高了巡飞弹向心攻击的作战效率，期望为巡飞弹向心攻击的进一步研究提供思路。

参考文献

[1]Beni G，Wang J.Swarm intelligence[C]//NATO Advanced Workshop on Robots and Biological Systems，Italy，1989：425-428.

[2]Colorni A，Dorigo M，Maniezzo V.Distributed optimiza-tion by ant colonies[C]//1st European Conference on Arti-ficial Life，Paris，1991：134-142.

[3]Yang X S.A new metaheuristic bat-inspired algorithm[J].Computer Knowledge & Technology，2010，284：65-74.

[4]Poli R，Kennedy J，Blackwell T.Particle swarm optimization[J].Swarm intelligence，2007（1）：33-57.

[5]Mirjalili S，Lewis A.The whale optimization algorithm[J].Advances in Engineering Software，2016， 95：51-67.

作者单位：陆军工程大学

责任编辑：张津平、尚丹