基于遗传算法优化支持向量回归的电池SOH预测

何山 郝雄博 赵宇明 姜颖 李昊巍

【摘要】针对实车运行过程中电池当前可用容量难获取、电池健康状态评估不准确的问题，提出利用车辆的停车充电片段数据，通过箱型图及卡尔曼滤波算法对安时积分法计算所得的电池容量进行修正，构建支持向量回归模型用于电池衰减预测，通过皮尔森相关性分析确定有效的模型输入参数，结合遗传算法优化模型参数。结果表明：优化后模型的拟合优度可达88%，相较于优化前提高了12%，可以实现电池健康状态的准确预测。

主题词：实车数据 动力电池 容量衰减 卡尔曼滤波 遗传算法 支持向量回归

中图分类号：U463.63   文献标志码：A   DOI： 10.19620/j.cnki.1000-3703.20230606

Battery SOH Prediction Based on Support Vector Regression Optimized by Genetic Algorithm

He Shan1， Hao Xiongbo2，3， Zhao Yuming1， Jiang Ying2，3， Li Haowei3

（1. Shenzhen Power Supply Bureau Co.，Ltd.， Shenzhen 518000; 2. Automotive Data of China （Tianjin） Co.， Ltd.， Tianjin 300000; 3. China Academy of Industrial Internet， Beijing 100000）

【Abstract】The current available capacity of the battery is difficult to obtain， and the health status of the battery is difficult to estimate accurately during the operation of the vehicle. Therefore， this paper proposed to use the parking and charging segment data of the vehicle to correct the battery capacity obtained by ampere-hour integration method through box diagram and Kalman filter algorithm. The support vector regression model was constructed for battery degradation prediction. The effective model input parameters were determined by Pearson correlation analysis. The model parameters were optimized by genetic algorithm. Results show that the fitting accuracy of the optimized model reaches 88%， which is 12% higher than that before optimization， can accurately predict the SOH of vehicle battery.

Key words： Vehicle data， Power battery， Capacity degradation， Kalman filter， Genetic algorithm， Support vector regression

【引用格式】 何山， 郝雄博， 赵宇明， 等. 基于遗传算法优化支持向量回归的电池SOH预测[J]. 汽车技术， 2024（5）： 31-36.

HE S， HAO X B， ZHAO Y M， et al. Battery SOH Prediction Based on Support Vector Regression Optimized by Genetic Algorithm[J]. Automobile Technology， 2024（5）： 31-36.

1 前言

动力电池作为新能源汽车核心动力源之一，是车辆保持良好运行状态的重要基础，进行电池健康状态监测对提高電池使用寿命以及安全性等方面具有重要意义。

动力电池健康状态（State of Health，SOH）与剩余使用寿命（Remaining Useful Life，RUL）预测方法分为基于模型、基于数据驱动及二者结合的方法[1]。基于数据驱动的方法只需根据电池使用数据即可实现预测，且应用广泛[2]。文献[3]利用美国航空航天局（National Aeronautics and Space Administration，NASA）和马里兰大学先进生命周期工程中心（Center for Advanced Life Cycle Engineering，CALCE）公开数据集，建立结合双重注意力机制的长短期记忆神经网络模型，联合预测电池SOH和RUL。文献[4]基于NASA数据，结合人工神经网络与粒子滤波算法，实现电池RUL的预测。文献[5]基于3组不同老化程度的电池数据，用前馈神经网络和循环神经网络预测电池电压曲线，基于曲线相似度估计电池容量和SOH。文献[6]利用NASA数据，提出一种基于改进粒子群优化极限学习机的SOH以及RUL估计方法。文献[7]通过提取充电实验数据的等电压差间隔时间等特征，应用长短期记忆网络（Long Short-Term Memory，LSTM）对电池SOH和RUL进行预测。文献[8]提出一个双向LSTM与注意机制模型预测RUL，并进行了验证。文献[9]利用NASA数据对非线性自回归外输入递归神经网络和时滞神经网络预测精度进行了评价。文献[10]利用NASA数据，通过卡尔曼滤波和粒子滤波算法修正电池容量值，再用极端梯度提升算法（eXtreme Gradient Boosting，XGBoost）进行电池RUL预测。

目前，针对电池SOH预测的研究大多采用公开数据集或实验室数据，较少采用实车数据，并且现有研究大多采用神经网络算法，虽具有较好预测精度，但其结构复杂，计算成本高。针对上述问题，本文基于实车数据提出一种基于遗传算法优化的支持向量回归方法进行电池健康状态预测，并针对数据噪声大、工况波动等问题制定修正方案，本研究可为新能源车辆电池状态监测、车辆维修保养计划制定及车用电池退役回收等提供依据。

2 基于遗传算法优化的支持向量回归方法

2.1 基础算法

支持向量回归（Support Vector Regression，SVR）是一种基于支持向量机的回归方法，具备非线性拟合能力强，逼近和泛化能力优越等优点，其基本原理是将原本特征空间的数据集变换到高维特征空间，从而可将低维非线性回归问题转化为高维线性回归问题，并基于不同核函数选择进行参数巡优，以提高模型预警精度[11-13]。

遗传算法（Genetic Algorithm，GA）是一种借鉴了生物进化的计算方法，通过模拟物种进化过程来寻找问题最优解，其核心思想是借助选择、交叉和变异过程不断优化种群中的个体，最终选出最优个体[14]。

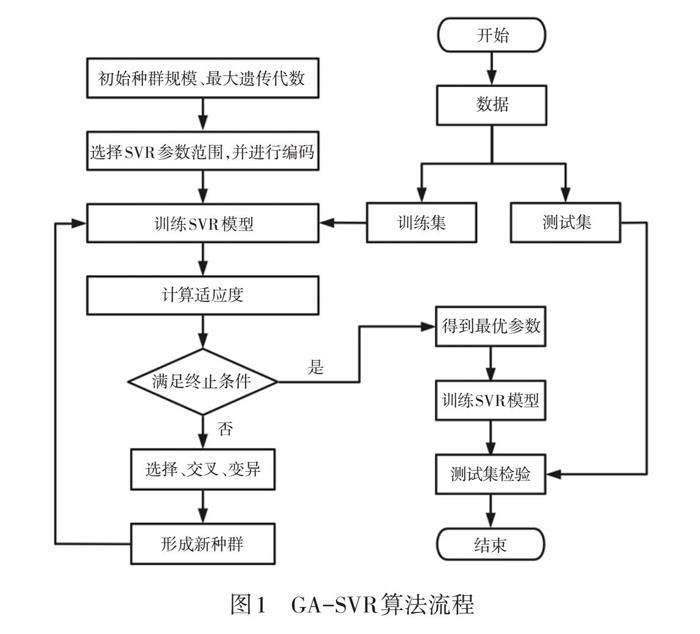
基于遗传算法优化的支持向量回归算法模型（GA-SVR）的核心思想是利用GA解决SVR模型参数优化问题，算法流程如图1所示，关键步骤如下：

a. 样本数据划分为训练集和测试集，样本数据包含最终确定的模型输入向量和用户定义的标签值。

b. 综合考虑个体多样性以及算法复杂度，设置初始种群规模及最大遗传代数。

c. 进行染色体基因编码，使每个染色体对应的基因编码为SVR的3个可调参数C、gamma、epsilon。

d. 在训练集上训练相应SVR模型，计算个体适应度。

e. 判断是否达到终止条件，未达到则根据个体适应度以及预先设置的几个遗传算子筛选出亲代个体，进行交叉、变异操作，完成种群基因编码的信息更新，返回步骤d继续执行直至满足终止条件，得到最优模型参数。

f. 用得到的最优参数训练SVR模型，并且用测试集数据检验模型效果。

2.2 GA-SVR算法应用

本文将GA-SVR算法用于新能源汽车电池健康状态的预测研究。首先需进行实车数据预处理，对异常数据进行清洗，根据车辆实际运行状态将全部数据划分为充电、放电及静置片段，筛选有效的数据片段提取电池衰减相关特征，以电池当前最大可用容量定义SOH，并针对实车数据噪声大、数值离散度高等问题采用箱型图及卡尔曼滤波算法进行修正，此后将修正后得到的SOH值作为标签，通过相关性分析确定输入特征向量，并进行归一化处理得到最终的样本数据，将其输入GA-SVR算法模型进行电池SOH的预测。

3 数据处理

3.1 数据来源及数据情况描述

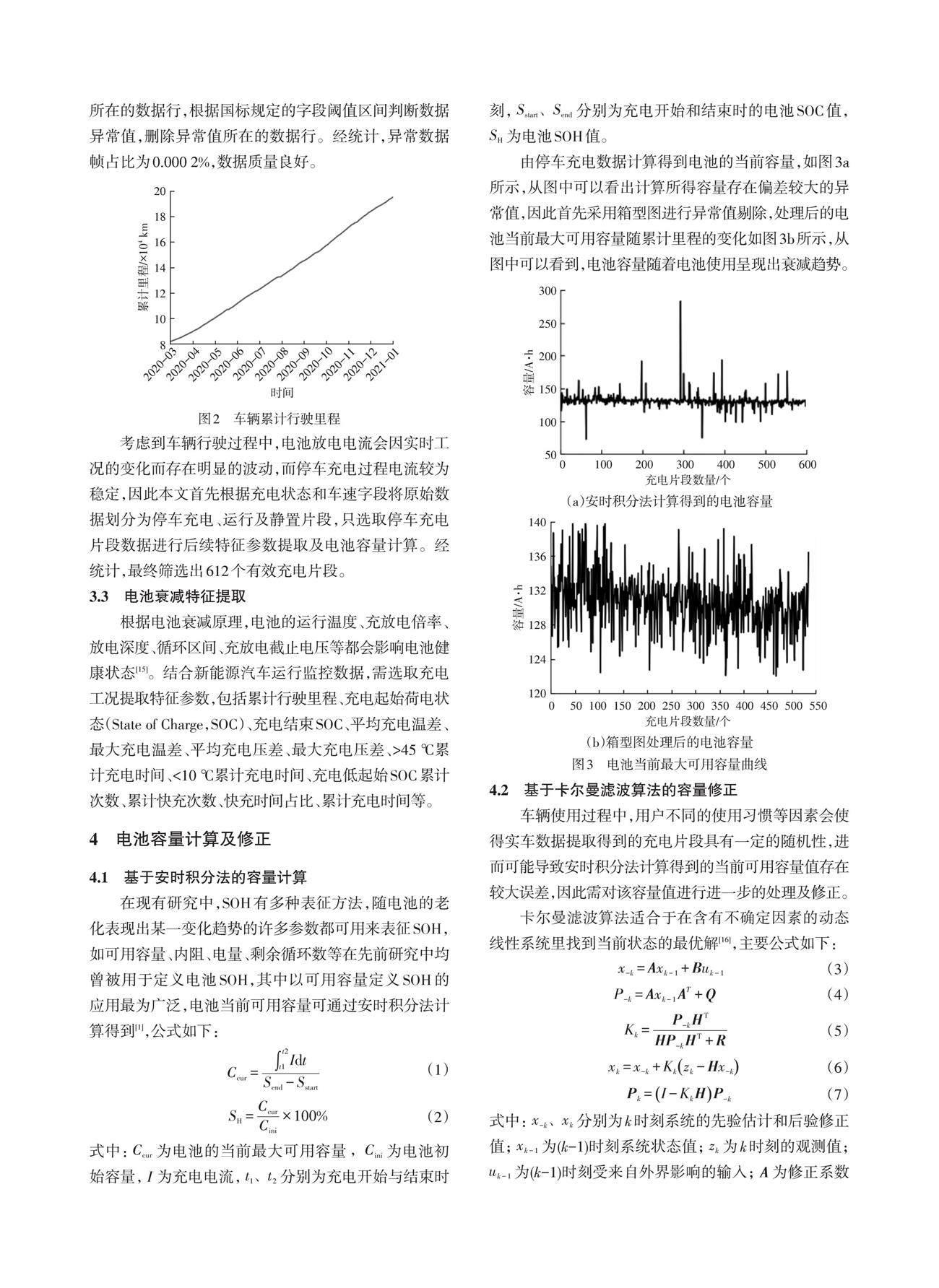
本文数据来源为某企业提供的一款纯电动汽车2020年3月～2020年12月的运行数据，累计行驶里程区间为8.15×104 ～1.95×105 km，如图2所示。数据传输协议遵循GB/T 32960—2016 《电动汽车远程服务与管理系统技术规范》的相关规定，采样间隔为10 s。

3.2 数据清洗与片段划分

原始数据存在时间乱序、数据缺失、数值异常等情况。首先按时间顺序，删除重复上传的时间帧以及空值所在的數据行，根据国标规定的字段阈值区间判断数据异常值，删除异常值所在的数据行。经统计，异常数据帧占比为0.000 2%，数据质量良好。

考虑到车辆行驶过程中，电池放电电流会因实时工况的变化而存在明显的波动，而停车充电过程电流较为稳定，因此本文首先根据充电状态和车速字段将原始数据划分为停车充电、运行及静置片段，只选取停车充电片段数据进行后续特征参数提取及电池容量计算。经统计，最终筛选出612个有效充电片段。

3.3 电池衰减特征提取

根据电池衰减原理，电池的运行温度、充放电倍率、放电深度、循环区间、充放电截止电压等都会影响电池健康状态[15]。结合新能源汽车运行监控数据，需选取充电工况提取特征参数，包括累计行驶里程、充电起始荷电状态（State of Charge，SOC）、充电结束SOC、平均充电温差、最大充电温差、平均充电压差、最大充电压差、>45 ℃累计充电时间、<10 ℃累计充电时间、充电低起始SOC累计次数、累计快充次数、快充时间占比、累计充电时间等。

4 电池容量计算及修正

4.1 基于安时积分法的容量计算

在现有研究中，SOH有多种表征方法，随电池的老化表现出某一变化趋势的许多参数都可用来表征SOH，如可用容量、内阻、电量、剩余循环数等在先前研究中均曾被用于定义电池SOH，其中以可用容量定义SOH的应用最为广泛，电池当前可用容量可通过安时积分法计算得到[1]，公式如下：

[Ccur=t1t2IdtSend-Sstart]                           （1）

[SH=CcurCini×100%]                         （2）

式中：[Ccur]为电池的当前最大可用容量[，Cini]为电池初始容量，[I]为充电电流，[t1、t2]分别为充电开始与结束时刻，[Sstart、Send]分别为充电开始和结束时的电池SOC值，[SH]为电池SOH值。

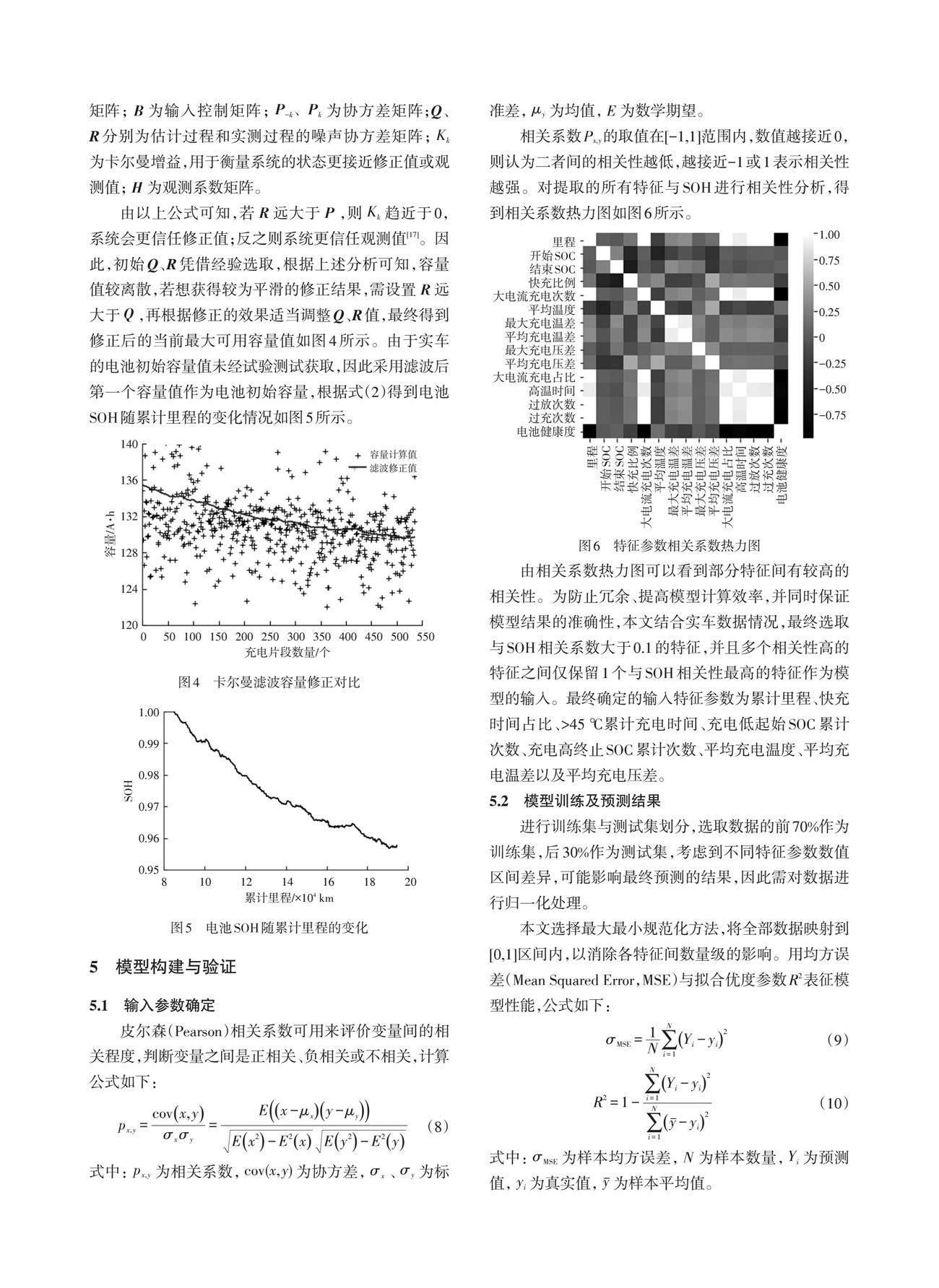
由停车充电数据计算得到电池的当前容量，如图3a所示，从图中可以看出计算所得容量存在偏差较大的异常值，因此首先采用箱型图进行异常值剔除，处理后的电池当前最大可用容量随累计里程的变化如图3b所示，从图中可以看到，电池容量随着电池使用呈现出衰减趋势。

4.2 基于卡尔曼滤波算法的容量修正

车辆使用过程中，用户不同的使用习惯等因素会使得实车数据提取得到的充电片段具有一定的随机性，进而可能导致安时积分法计算得到的当前可用容量值存在较大误差，因此需对该容量值进行进一步的处理及修正。

卡尔曼滤波算法适合于在含有不确定因素的动态线性系统里找到当前状态的最优解[16]，主要公式如下：

[x-k=Axk-1+Buk-1]                          （3）

[P-k=Axk-1AT+Q]                            （4）

[Kk=P-kHTHP-kHT+R]                         （5）

[xk=x-k+Kkzk-Hx-k]                      （6）

[Pk=I-KkHP-k]                        （7）

式中：[x-k、xk]分别为k时刻系统的先验估计和后验修正值；[xk-1]为（k-1）时刻系统状态值；[zk]为k时刻的观测值；[uk-1]为（k-1）时刻受来自外界影响的输入；[A]为修正系数矩阵；[B]为输入控制矩阵；[P-k、Pk]为协方差矩阵；Q、R分别为估计过程和实测过程的噪声协方差矩阵；[Kk]为卡尔曼增益，用于衡量系统的状态更接近修正值或观测值；[H]为观测系数矩阵。

由以上公式可知，若[R]远大于[P]，则[Kk]趋近于0，系统会更信任修正值；反之则系统更信任观测值[17]。因此，初始Q、R凭借经验选取，根据上述分析可知，容量值较离散，若想获得较为平滑的修正结果，需设置[R]远大于[Q]，再根据修正的效果适当调整Q、R值，最终得到修正后的当前最大可用容量值如图4所示。由于实车的电池初始容量值未经试验测试获取，因此采用滤波后第一个容量值作为电池初始容量，根据式（2）得到电池SOH随累计里程的变化情况如图5所示。

5 模型构建与验证

5.1 输入参数确定

皮尔森（Pearson）相关系数可用来评价变量间的相关程度，判断变量之间是正相关、负相关或不相关，计算公式如下：

[px，y=covx，yσxσy=Ex-μxy-μyEx2-E2xEy2-E2y]    （8）

式中：[px，y]为相关系数，[cov（x，y）]为协方差，[σx]、[σy]为标准差，[μy]为均值，[E]为数学期望。

相关系数Px，y的取值在[-1，1]范围内，数值越接近0，則认为二者间的相关性越低，越接近-1或1表示相关性越强。对提取的所有特征与SOH进行相关性分析，得到相关系数热力图如图6所示。

由相关系数热力图可以看到部分特征间有较高的相关性。为防止冗余、提高模型计算效率，并同时保证模型结果的准确性，本文结合实车数据情况，最终选取与SOH相关系数大于0.1的特征，并且多个相关性高的特征之间仅保留1个与SOH相关性最高的特征作为模型的输入。最终确定的输入特征参数为累计里程、快充时间占比、>45 ℃累计充电时间、充电低起始SOC累计次数、充电高终止SOC累计次数、平均充电温度、平均充电温差以及平均充电压差。

5.2 模型训练及预测结果

进行训练集与测试集划分，选取数据的前70%作为训练集，后30%作为测试集，考虑到不同特征参数数值区间差异，可能影响最终预测的结果，因此需对数据进行归一化处理。

本文选择最大最小规范化方法，将全部数据映射到[0，1]区间内，以消除各特征间数量级的影响。用均方误差（Mean Squared Error，MSE）与拟合优度参数R2表征模型性能，公式如下：

[σMSE=1Ni=1NYi-yi2]                         （9）

[R2=1-i=1NYi-yi2i=1Ny-yi2]                           （10）

式中：[σMSE]为样本均方误差，[N]为样本数量，[Yi]为预测值，[yi]为真实值，[y]为样本平均值。

由式（10）可知[R2]在[0，1]范围内，越接近1则表示回归拟合效果越好，一般认为超过0.8则判断模型拟合优度较高。

先根据经验手动设置SVR模型超参数：惩罚因子[C=10]，核函数参数[γ=0.1]，损失函数容差限制参数[e=0.1]。得到模型[σMSE=0.000 85]、[R2=0.76]，结果如图7所示。

训练GA-SVR模型，将适应度函数设为相对误差绝对值的倒数，设置惩罚因子[C∈[0，100]]，核函数参数[γ∈0.01，1]，损失函数容差限制参数[e∈0.01，1]，种群规模设置为20，交叉概率为0.7，变异概率为0.01，设置进化代数为200，得到进化过程适应度曲线如图8所示。

經遗传算法优化后得到模型的最优参数分别为：惩罚因子[C=42.808 7]，核函数参数[γ=0.046 7]，损失函数容差限制[e=0.116 3]，优化后模型[σMSE=0.000 42]，[R2=0.88]，优化前后预测结果对比如图9、图10所示，可看到经遗传算法优化后，模型的预测精度明显提高。

6 结束语

本文提出一种基于实车数据的车用动力电池衰减预测方法，选取停车充电片段数据计算电池当前最大可用容量，并用箱型图及卡尔曼滤波修正计算所得的容量值，并通过皮尔森相关系数进行特征参数相关性分析，筛选有效特征作为GA-SVR模型的输入，进行电池SOH的预测。模型预测结果表明，SVR方法具有优良的时间序列回归预测性能，结合遗传算法进行参数寻优可以显著提高模型预测的准确性。通过绘制SOH随行驶里程的衰减曲线进一步分析车辆剩余行驶里程，可为车用电池的退役回收等提供依据。

参 考 文 献

[1] 赵珈卉， 田立亭， 程林. 锂离子电池状态估计与剩余寿命预测方法综述[J]. 发电技术， 2023， 44（1）： 1-17.

ZHAO J H， TIAN L T， CHENG L. Review of State             Estimation and Remaining Useful Life Prediction for       Lithium-Ion Batteries[J]. Power Generation Technology， 2023， 44（1）： 1-17.

[2] 于海芳， 陈文帅. 锂离子电池寿命预测技术综述[J]. 电源技术， 2018， 42（2）： 304-307.

YU H F， CHEN W S. Overview of Lithium-Ion Battery Life Prediction Technology[J]. Power Supply Technology， 2018， 42（2）： 304-307.

[3] 戴俊彦， 夏明超， 陈奇芳. 基于双重注意力机制的电池SOH估计和RUL预测编解码模型[J]. 电力系统自动化， 2023， 47（6）： 168-177.

DAI J Y， XIA M C， CHEN Q F. Battery SOH Estimation and RUL Prediction Codec Model Based on Dual Attention Mechanism[J]. Power System Automation， 2023， 47（6）： 168-177.

[4] 晋殿卫， 顾则宇， 张志宏. 锂电池健康度和剩余寿命预测算法研究[J]. 电力系统保护与控制， 2023， 51（1）： 122-130.

JIN D W， GU Z Y， ZHANG Z H. Research on Lithium     Battery Health and Residual Life Prediction[J]. Power      System Protection and Control， 2023， 51（1）： 122-130.

[5] 刘良俊， 高一钊， 朱景哲， 等. 数据驱动的锂离子电池健康状态估计[J]. 电池， 2022， 52（2）： 157-161.

LIU L J， GAO Y Z， ZHU J Z， et al. Data-Driven               Lithium-Ion Battery State of Health Estimation[J]. Battery， 2022， 52（2）： 157-161.

[6] ZHANG C Y， WANG S L， YU C M， et al. Improved Particle Swarm Optimization-Extreme Learning Machine Modeling Strategies for the Accurate Lithium-Ion Battery State of Health Estimation and High-adaptability Remaining Useful Life Prediction[J]. Journal of the Electrochemical Society， 2022， 169（8）.

[7] KWON S， HAN D H， PARK J， et al. Joint State-of-Health and Remaining-Useful-Life Prediction Based on  Multi-Level Long Short-Term Memory Model Prognostic Framework Considering Cell Voltage Inconsistency Reflected Health Indicators[J]. Journal of Energy Storage， 2022， 55.

[8] WANG F K， AMOGNE Z E， CHOU J H， et al. Online        Remaining Useful Life Prediction of Lithium-Ion Batteries Using Bidirectional Long Short-Term Memory with            Attention Mechanism[J]. Energy， 2022， 254.

[9] BAMATI S， CHAOUI H. Lithium-Ion Batteries Long        Horizon Health Prognostic Using Machine Learning[J]. IEEE Transactions on Energy Conversion， 2022， 37（2）： 1176-1186.

[10] JAFARI S， BYUN Y C. XGBoost-Based Remaining Useful Life Estimation Model with Extended Kalman Particle     Filter for Lithium-Ion Batteries[J]. Sensors， 2022， 22（23）： 9522.

[11] CORTES C， VAPNIK V. Support-Vector Networks[J].    Machine Learning， 1995， 20（3）： 273-297.

[12] 韩伟， 王帅， 张筱辰， 等. 基于不同核函数SVR的锂离子电池SOH预测比较[J]. 电源技术， 2021， 45（3）： 362-365+ 377.

HAN W， WANG S， ZHANG X C， et al. Comparison of SOH Prediction of Lithium-Ion Batteries Based on SVR with   Different Kernel Functions[J]. Power Technology， 2021， 45（3）： 362-365+377.

[13] 李龙刚， 李立伟， 杨玉新， 等. 基于改进灰狼优化与支持向量回归的锂电池健康状态预测[J]. 南京理工大学学报（自然科学版）， 2020， 44（2）： 154-161+170.

LI L G， LI L W， YANG Y X， et al. Lithium Battery Health Status Prediction Based on Improved Grey Wolf               Optimization and Support Vector Regression[J]. Journal of Nanjing University of Science and Technology （Natural    Science Edition）， 2020， 44（2）： 154-161+170.

[14] 胡慧敏. 车用锂离子电池健康状态估计及剩余寿命预测[D]. 西安： 长安大学， 2020.

HU H M. State of Health Estimation and Remaining Useful Life Prediction of Lithium-Ion Batteries for Vehicles[D].   Xian： Changan University， 2020.

[15] 王文博. 热-电耦合老化路径下动力电池的衰减机理研究[D]. 哈尔滨： 哈尔滨理工大学， 2020.

WANG W B. Study on the Attenuation Mechanism of     Power Battery Under Thermal-Electric Coupling Aging Path[D]. Harbin： Harbin University of Science and            Technology， 2020.

[16] TONG G， CAI J， HUANG L， et al. A Modified Extend     Kalman Filter Based Approach for Lithium-Ion Battery Rul Prognosis[C]. Xian： IEEE 5th Information             Technology， Networking， Electronic and Automation      Control Conference （ITNEC）， 2021.

[17] 周雅夫， 史宏宇. 面向实车数据的电动汽车电池退役轨迹预测[J]. 太阳能学报， 2022， 43（5）： 510-517.

ZHOU Y F， SHI H Y. Trajectory Prediction of Electric    Vehicle Battery Retirement for Real Vehicle Data[J].         Journal of Solar Energy， 2022， 43（5）： 510-517.

（責任编辑 王 一）

修改稿收到日期为2023年8月23日。