基于频率测试的斜交小箱梁桥梁格模型研究

宋锋

摘要 装配式小箱梁桥横向刚度模拟方法直接影响结构的内力分布，然而，目前斜交小箱梁桥梁格模型研究较少。文章以3座不同斜交角25 m跨径的箱梁桥为对象，采用不同的横向刚度模拟方法计算桥梁的自振频率，并与实测结果进行比较。结果表明，梁端刚域模拟方法与实测结果最为接近，采用顶板截面模拟横向刚度与实测结果偏差较大。

关键词 斜交；小箱梁；梁格模型；横向刚度；自振频率

中图分类号 U448.213文献标识码 A文章编号 2096-8949（2024）06-0022-03

0 引言

装配式预应力混凝土小箱梁是公路桥梁中一种应用非常广泛的结构形式，设计或检测单位一般采用梁格法对其进行计算分析。为使计算模型能够较为准确地反映结构的实际受力状态，部分学者对装配式小箱梁桥的梁格模型尤其是虚拟横梁的设置方法进行了研究。韩智强[1]等按照截面形式将相邻两片箱梁之间的虚拟横梁分成顶板、二字形和过渡截面几部分；郭小权[2]等以一座3×30 m小箱梁为例，以等代简支梁理论和实体模型计算结果为标准，比较了汽车荷载作用下梁格模型不同虚拟横梁设置方式下结构横向分布系数的偏差，认为梁端刚域法模拟虚拟横梁全面可靠；杨圣超[3]等对小箱梁桥梁格模型中虚拟横梁刚域长度进行了深入研究，通过与车辆荷载作用下实测主梁挠度和应变进行比较，推荐自纵梁中心开始到纵梁腹板内侧边缘为止设置为虚拟横梁的梁端刚域。

然而，当前研究大多集中于直桥，斜、弯小箱梁桥的梁格模型相关研究较少。梁格模型是利用纵、横向梁格刚度来模拟实际空间结构刚度分布，而结构的动力特性（包括结构的自振频率及振型等）可以直接反映刚度分布情况，并已在有限元模型修正技术中被广泛应用[4-6]。鉴于此，该文基于两座不同斜交角的简支小箱梁桥的频率测试结果，对斜交小箱梁桥梁格模型的合理设置方式进行研究。

1 工程概况

1.1 桥梁概况

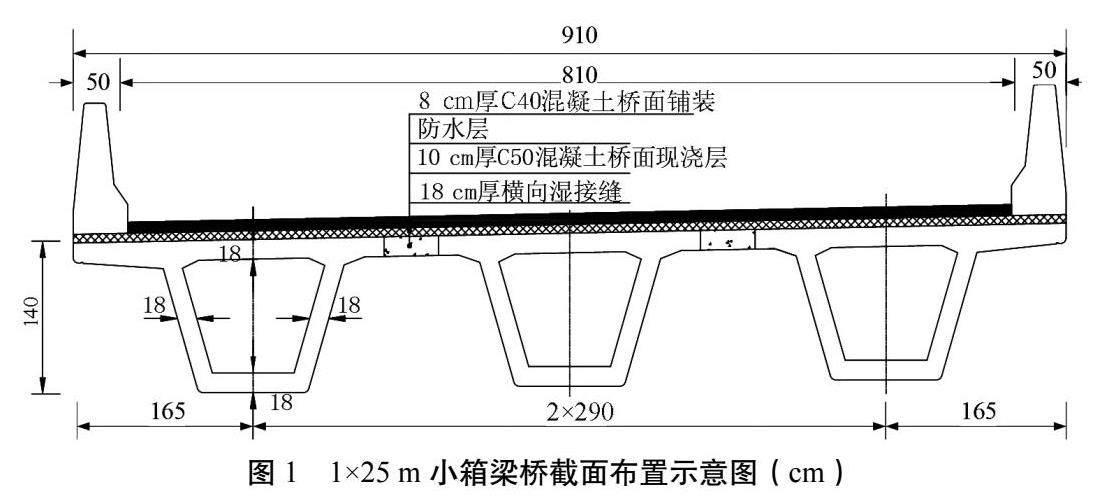
该文以国道219线上3座1×25 m简支小箱梁桥为研究对象，3座桥梁位于同一标段，均建于2010年，其中一座为直桥，另两座斜交角分别为15 °和30 °。3座桥截面布置相同，如图1所示。

1.2 自振频率测试

该文采用东华测试的DH5922動力特性测试分析系统对3座桥梁的自振频率进行了现场测试。

2 有限元模型

为了对测试结果进行深入分析，该文采用Midas/Civil对试验桥梁建立了有限元模型。混凝土材料弹性模量是桥梁结构有限元模拟的重要参数，而混凝土弹性模量设计值，通常要比实际弹性模量小很多，直接影响到分析结果的可靠性。为提高计算精度，该文计算模型所用混凝土弹性模量均采用现场回弹测试结果。

3座桥梁支座布置类似，两端均采用GYZ D400×84板式橡胶支座。由于斜交桥弯扭耦合振型的存在，支座模拟方法可能对结构计算频率影响较大。为尽量逼近实际情况，该文采用在梁底设置线性弹簧的方式来模拟支座。

3座桥梁的桥面铺装均由10 cm厚C50现浇调平层和8 cm厚C40防水混凝土层组成，许多学者对桥面混凝土铺装层与主梁的共同作用进行了研究。石雄伟[7]等以 114 座预应力混凝土连续箱梁及空心板桥作样本，计算了混凝土桥面铺装层厚度对荷载试验校验系数的影响，通过对计算结果进行统计回归分析，认为应考虑桥面铺装对主梁受力影响，尽可能将理论计算接近桥梁实际情况。钱寅泉[8]等通过单梁和实桥试验对比了铺装前后小箱梁桥的挠度变化，认为一般情况下约70%的混凝土铺装层参与小箱梁共同受力。结合以上研究和试验对象现状，该文考虑12 cm厚的混凝土铺装层与主梁共同受力，其余6 cm厚铺装层作为外部荷载施加于主梁结构。

试验对象桥面两侧均设置钢筋混凝土防撞护栏，考虑防撞护栏每隔8～10 m设置一条4 cm宽变形缝，并非沿全桥连续布置，故将防撞护栏模拟为外部荷载作用在主梁两侧相应位置，不考虑其对主梁刚度的贡献，并尽量使计算模型质量分布逼近实际情况。

综合已有的研究成果，该文分别采用三种方式模拟小箱梁桥的虚拟横梁：

（1）顶板截面模型，即虚拟横梁截面高度采用箱梁的顶板厚度。

（2）分段截面模型，即将虚拟横梁分为翼缘和箱室两部分，其中翼缘部分横梁高度用顶板厚度，箱室部分横梁采用箱梁顶板和底板厚度组成的二字形截面。

（3）梁端刚域模型，与分段截面模型相似，只不过将箱室范围的虚拟横梁用刚域代替。

3 结果分析

该文对每座桥梁建立3个有限元模型，对其振型分布和自振频率进行研究。其中模型1的虚拟横梁采用顶板截面模型，模型2的虚拟横梁采用分段截面模型，模型3的虚拟横梁采用梁端刚域模型。

3.1 横梁模拟方法对振型分布的影响

不同横梁模拟方式下，桥梁的振型分布未发生改变，先后顺序均表现为一阶对称竖向弯曲振型、横向扭转振型、略带扭转的一阶反对称竖向弯曲振型。

3.2 横梁模拟方法对结构自振频率的影响

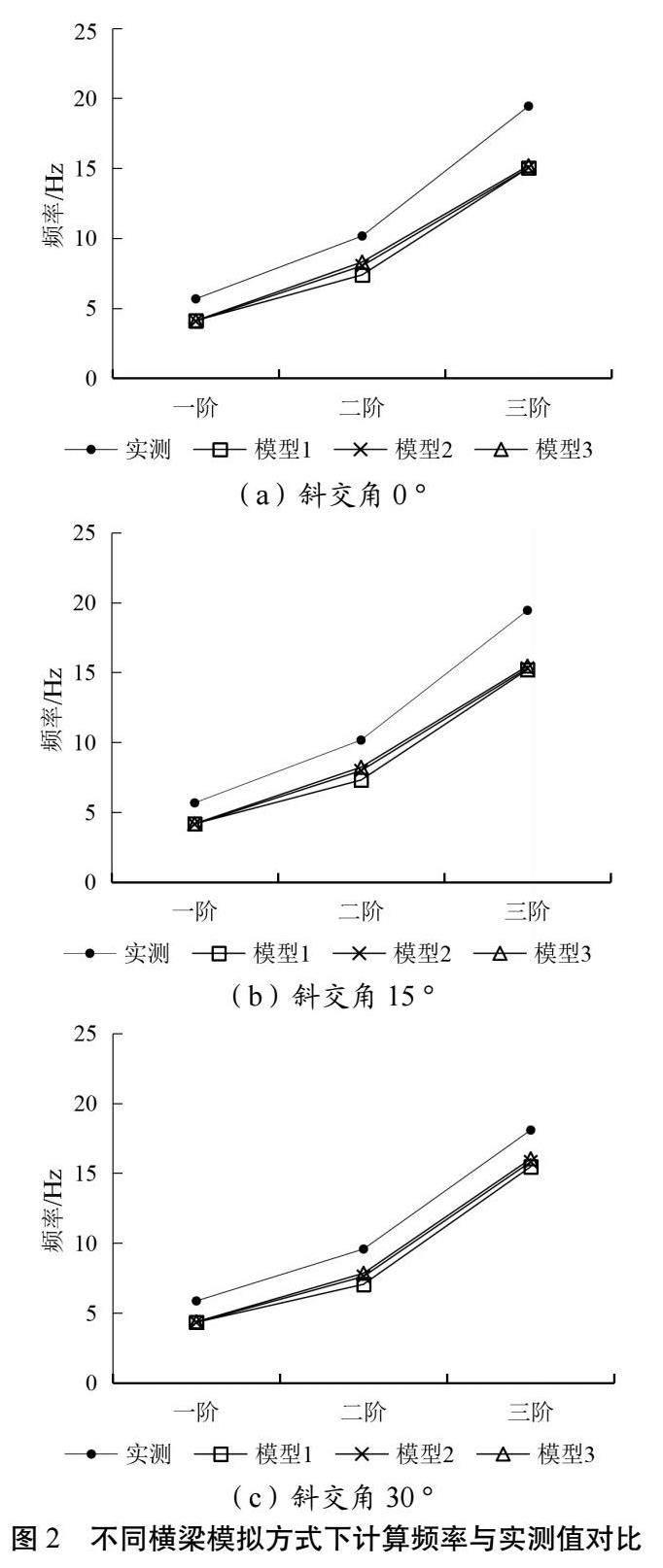
不同横梁模拟方法下计算频率与实测结果如图2所示。由图2可以看出，计算频率均小于实测频率，此时计算模型未考虑预应力钢束、构造钢筋等因素。

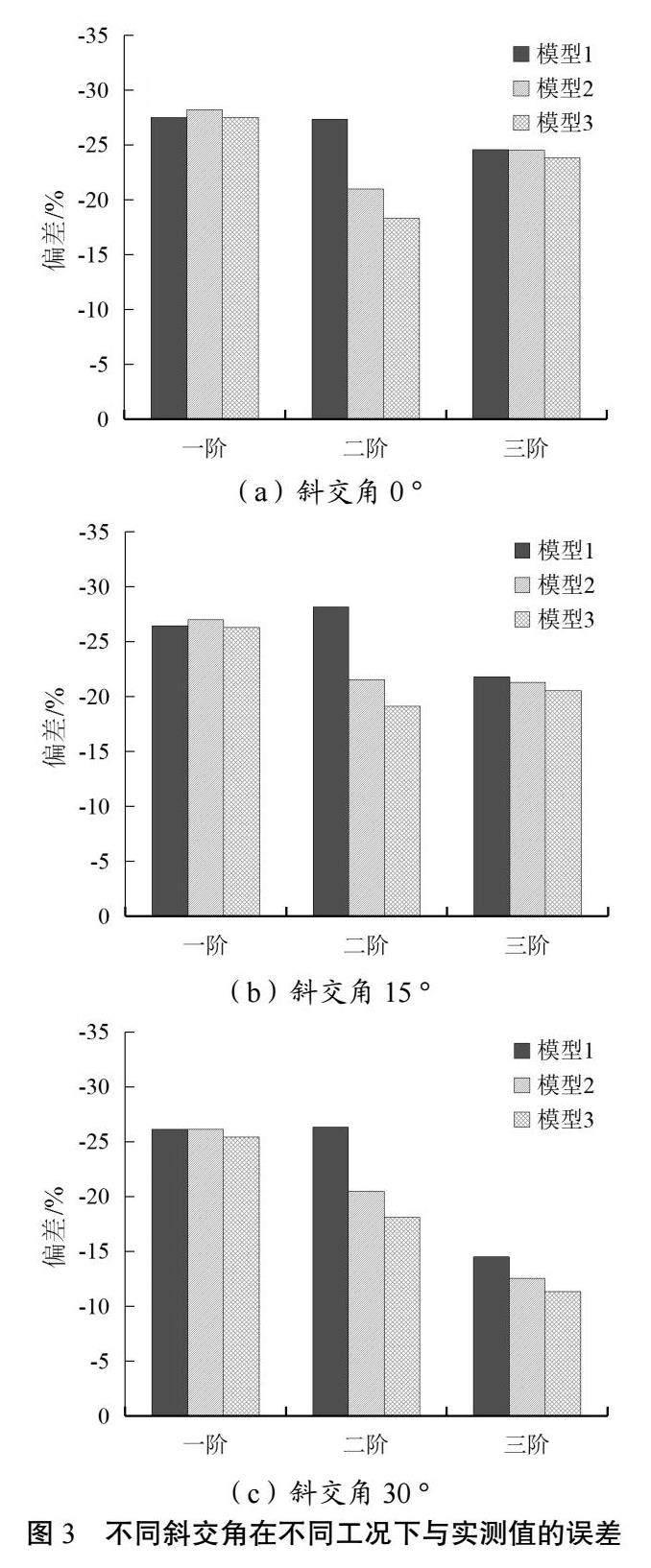
为了更清晰的展示横梁模拟方式对自振频率的影响，该文以实测频率为基准，对比各模型计算频率与实测频率的偏差，如图3所示，可以看出：

（1）横梁模拟方式对一阶、三阶频率影响不大，对二阶频率影响明显。考虑一阶振型为一阶对称竖向弯曲振动，三阶振型为一阶反对称竖向弯曲振动，不难分析出，竖向弯曲振型对应的自振频率对横梁模拟方式不敏感。

（2）横梁模拟方式对二阶频率影响明显，其中顶板截面模型与实测频率偏差最大，达到25%；梁端刚域模型与实测频率偏差最小，为17%。说明横梁模拟方式主要影响结构的横向刚度分布，进而影响扭转振型的自振频率，梁端刚域模型最接近结构的实际状态。

通过分析，对于不同斜交角小箱梁桥，三种工况下计算得的前三阶振型频率均与实测值存在一定偏差，随着斜交角的最大偏差有减小趋势，其中第三阶最明显由25%降到10%左右。不同工况下，第一阶振型频率偏差变化不大，基本在27%左右。第二阶振型频率偏差变化较大，其中工况一（即一字式虚拟横梁）偏差最大，达25%。工况二（分段式虚拟横梁）偏差次之，为20%。工况三（梁端刚域式虚拟横梁）偏差最小，为17%。不同斜交角有相同的规律，第三阶振型频率偏差变化随斜交角的增大而增大。

由此可见，不同工况（即不同虚拟横梁模拟方法）对第二阶振型频率计算值影响较大，第二阶振型为横向扭转振型，表明不同虚拟横梁模拟方法下主梁横向扭转刚度会有较大不同。工况三（梁端刚域式虚拟横梁）第二阶振型频率偏差最小，说明了梁端刚域式虚拟横梁模拟方法最能接近桥梁实际横向扭转刚度。

4 结论

该文以3座不同斜交角（0 °、15 °、30 °）小箱梁桥为对象，比较了顶板截面模型、分段截面模型、梁端刚域模型三种不同虚拟横梁模拟方法下的桥梁前三阶振型分布和自振频率，并与实测频率进行比较，得到以下结论：

（1）横梁模拟方法不会改变斜交小箱梁桥的振型分布顺序。

（2）横梁模拟方式对竖向弯曲振型的自振频率影响不明显，对扭转振型影响明显。

（3）采用顶板截面模型的横梁模拟方式与实际偏差较大，梁端刚域模型最接近结构实际状态。

参考文献

[1]韩智强，申林，倪富陶，等. 3×30 m连续小箱梁虚拟刚度分析研究[J]. 中外公路， 2016（2）： 78-81.

[2]郭小权， 庞浩然， 张超. 连续小箱梁桥虚拟横梁刚度模拟研究[J]. 公路交通技术， 2018（1）： 48-53.

[3]杨圣超， 夏兴佳. 基于梁格法的预制箱梁横向刚度模拟研究[J]. 世界桥梁， 2016（2）： 73-76.

[4]王富万， 杨文兵. 梁格法在桥梁上部结构分析中的应用[J]. 华中科技大学学报（城市科学版）， 2006（S1）： 80-82+90.

[5]葛俊穎， 丁啸宇. 梁格法分析铰接板梁桥虚拟横梁刚度的取值研究[J]. 公路， 2010（4）： 103-106.

[6]冯文焕， 苏巨峰. 梁格法分析小箱梁桥虚拟横梁刚度模拟[J]. 山西建筑， 2013（10）： 148-149.

[7]石雄伟， 雷丹， 袁卓亚， 等. 桥面铺装对中小跨径PC梁桥校验系数影响分析[J]. 应用基础与工程科学学报， 2015（4）： 792-804.

[8]钱寅泉， 周正茂， 袁桂芳， 等. 桥面铺装与小箱梁的共同作用试验[J]. 公路交通科技， 2012（2）： 82-86.