浅析火星低重力模拟试验平台设计

黄科，董强，陈强，邢伟，程刚

（北京特种工程设计研究院，北京 100028）

受火星特殊行星条件影响，火星探测任务在着陆阶段有巨大困难，在我国实施火星探测任务前，美国、苏联、欧空局等已经多次向火星发射探测器，但成功率仅为51.11%。围绕着陆阶段的控制系统设计开展研究及地面验证试验，是确保火星探测任务成功的关键研究内容之一。在火星探测器着陆阶段中面临的工作环境重要特点之一是低重力，需要在地面预先研究低重力模拟平台，验证探测器在火星进行着陆缓冲过程中的关键技术问题。

1 系统总体设计

在地面实现低重力模拟技术的主要方法包括落塔法、抛物飞行法、水浮法、气浮法、悬吊法、外骨骼法和机械臂托举法，其中的悬吊法是目前综合优势最大、研究成果最多的低重力模拟技术。模拟试验平台要实现水平两自由度大范围跟踪探测器运动，在水平高精度跟踪运动的同时，还要跟踪探测器垂直方向大范围的高速移动，同时随动系统在跟随过程中要满足吊绳绝对倾角的要求，具备足够的向上加速度、最大垂直跟踪速度和拉力控制精度的能力，实质上试验平台的研制就是要在大空间内对飞行中的探测器实施高精度的三维位置与拉力混合随动控制。

模拟试验平台要实现水平两自由度大范围（20m×20m）跟踪火星探测器运动，水平跟踪加速度1.5m/s2，最大跟踪速度为5m/s。一方面，随动系统应满足吊绳的绝对倾角的要求，即随动系统运动过程中，与万向吊具连接处吊绳拉力方向与垂直方向的夹角不大于±0.1°。另一方面，在水平高精度跟踪运动的同时，还要跟踪探测器垂直方向大范围的高速移动，具备2.6m/s2的向上加速能力，且最大跟踪速度为10m/s，同时，要控制钢丝绳的拉力，在提供20000N 恒拉力时实现20N的拉力控制精度。

模拟试验平台主体结构为六个九柱桁架式钢管混凝土塔架，在塔顶部设悬挑桁架，悬挑桁架端部通过桁架将六塔连通，主体结构三维模型如图1。

图1 主体结构三维模型图

模拟试验平台控制系统主要由并联索驱动系统和快速随动系统组成。并联索驱动装置及控制单元沿圆周方向均匀布置在机房内，塔体及地面设置一定数量的转向滑轮，钢丝绳从塔柱的出绳点设置摆轮装置以驱动随动平台的快速随动。并联索驱动系统完成随动平台大范围的移动和跟踪；快速随动系统直接和试验验证器相连，高动态响应确保验证器在竖直方向的吊绳偏角和拉力控制精度。

2 并联索驱动系统设计

并联索驱动系统由主提升索驱动系统、上水平索驱动系统和下水平索驱动系统组成。

主提升索驱动系统由6 组驱动单元组成，每组驱动单元包括双电机、双减速器和双出绳滚筒。两根钢丝绳通过主体结构顶部距地面133 米高度处的两个滑轮与快速随动系统连接，构成平行四边形机构，防止快速随动系统产生倾斜。

上水平索驱动系统由6 组驱动单元组成，每组驱动单元包括电机、减速器和双出绳滚筒。两根钢丝绳通过主体结构柱腿上距地面77m 高度处水平布置的两个滑轮与快速随动系统连接，同样构成平行四边形机构，主要为快速随动系统提供水平驱动力和增加扭转刚度。

下斜拉索驱动系统与上水平索驱动系统结构上基本相同，双钢丝绳通过主体结构柱腿上距地面20m 高度处水平布置的两个滑轮与快速随动系统连接，同样构成平行四边形机构并为快速随动系统提供水平驱动力和增加扭转刚度。其中一组驱动单元采用双电机驱动来增加驱动力，将快速随动系统牵引到探测器转运区。

并联驱动系统采用一套运动控制器分别控制25 套伺服驱动器和交流电机来驱动减速器和滚筒，实现36 根钢丝绳跟随快速随动系统运动，为验证器和快速随动系统圆盘提供水平与垂直驱动力。控制输入是根据快速随动系统的位移计算的，需提前设置同步控制模式，系统实时读取圆盘位置坐标，实时计算位移增量并修改同步数据。

3 快速随动系统设计

快速随动系统通过36 根钢丝绳与并联索驱动系统相连，其包括水平快速随动子系统和拉力调节子系统，水平快速随动子系统提供水平拉力，拉力调节子系统实现对探测器拉力的精确控制。

3.1 水平快速随动子系统设计

快速随动装置由二维工作台组成，采用伺服电机、精密滚动导轨及滚轮齿条传动系统组合而成。

工作在随动控制方式，以实现水平快速随动系统中的上吊点对探测器的精确跟踪，其中跟踪误差的检测是通过实时读取吊点处的偏角检测编码器和安装在两维工作台处的激光陀螺仪的反馈数据实现，系统可以实现全闭环控制。绝对编码器的角度检测精度可达0.011°，激光陀螺仪的漂移小于0.01°/h，探测器吊绳倾角的检测精度可达0.03°。

控制输入来自探测器的水平移动，系统实时读取编码器、陀螺仪的测量值并且实时计算倾角和位移量数值，根据计算结果实时修改系统同步数据。

3.2 拉力调节子系统设计

拉力调节装置由粗精两级调节机构组成，安装在快速随动装置的两维工作台上，包括三台伺服电机、力传感器和传动机构。其中，功率较大的两台伺服电机完成拉力粗控制，主要起卸荷作用，可承载大部分探测器拉力载荷，以保证小功率伺服电机具有合适的拉力调节范围；小功率伺服电机工作在拉力闭环控制方式，实现探测器拉力的精确控制。

拉力调节子系统直接跟随探测器上吊点的垂直运动，由运动控制器控制两套伺服驱动器和伺服电机来实现拉力的精确闭环控制，伺服电机工作在扭矩控制方式，拉力的精确测量直接由上吊点处的力传感器来完成，整个系统工作在全闭环控制方式。

拉力传感器的非线性度为0.025%，在2 吨额定量程下的力检测精度5N，拉力的控制精度取决于电机的输出转矩，一般伺服电机的扭力控制精度为0.5%～1.5%。为适应下降阶段和上升阶段的载荷重量差别，优化拉力分配，实现20N 的拉力控制精度。

4 并联驱动控制算法设计

根据驱动索数m 与活动平台自由度n 的关系，索并联机构分为(mn+1) 三类，即非完全约束机构、完全约束机构、冗余约束机构。快速随动圆盘仅有6 个自由度，通过18 根钢丝绳与其相连,因此本系统属于冗余约束机构。为系统建立如图2 所示坐标系，一个是全局固定坐标O-XYZ，坐标原点O 在试场地面驱动系统的对称中心，坐标轴Z正向垂直向上，另一个坐标系是与快速随动圆盘固联的局部坐标系P-XYZ，坐标原点P 位于快速随动圆盘几何对称中心。Ai为第i 根索与塔架的连接点，Bi 为第i 根索与快速随动圆盘的连接点。

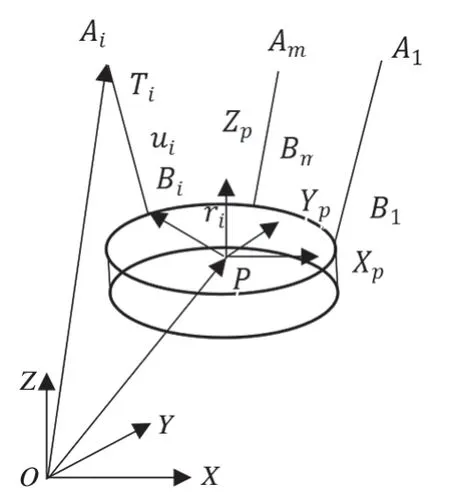
图2 系统坐标系

J 为与快速随动圆盘姿态和索张力方向相关的雅可比矩阵，W 为索并联系统的广义力。

式中J+是J 的Moor-Penrose 广义逆，J+=J+(JJT)-1。

K1为系统被动刚度，与系统位置姿态有关；K2为主动系统刚度，与系统位置姿态变化率及钢索张力T 大小有关。

综合以上结果：

由式（4）可知，索并联系统被动刚度与钢丝绳切线刚度有关，对于大跨度索并联系统，钢丝绳在自重影响下变成悬链线，不能直接用直线模型替代，因此其切线刚度需要考虑重力影响。

假设钢丝绳在空间通过两点A 和B，且B 点高于A 点，在包含A、B 两点的铅垂平面内，建立平面直角坐标系，并将A 选为坐标原点，同时使B 点位于第一象限，水平轴和垂直轴分别用X、Y 表示。假设钢丝绳的线密度为q，长为L，l 为钢索水平跨度，h 为钢索两端相对高度，H和V 分别为索张力T 的水平和垂直分量，且H 沿整个索长是不变量，钢丝绳的悬链线方程可表示为：

其中C 和D 为常数。

在圆盘钢丝绳连接处索力

当圆盘位置发生微小位移时，钢索悬跨度l 和相对高度h 发生变化，从而导致索张力T 发生变化。依据文献[5] ，切线刚度定义为：

当ql/H<=0.5 时，忽略高阶小量后

其中：

5 结语

火星低重力模拟试验平台提供模拟接近火星表面最后100m 时的试验空间。2021 年5 月15 日,中国火星探测器天问一号成功软着陆于火星乌托邦平原，突显了此项目试验平台对天问一号验证器的试验充分性和设计评估正确性。