抢险车对92 m跨度复合材料桁架桥动态响应的影响

孙泽阳 刘阳 杨俊锋 吴必涛 赵启林

DOI： 10.3969/j.issn.1671-7775.2024.03.014

开放科学（资源服务）标识码（OSID）：

摘要： 为研究大跨径桁架式纤维增强复合材料（FRP）应急抢修桥梁成桥后的动力性能，基于导梁推送施工92 m跨度的FRP桁架桥模型，编制FRP桁架桥的车桥耦合算法，研究抢险车辆的车速、质量及路面不平顺对FRP 桁架桥的跨中竖向位移、竖向加速度和关键杆件轴向应力等指标的影响.结果表明：路面越不平顺，车辆对桥梁结构的冲击作用越大，且路面等级对竖向位移的影响大于对关键杆件轴向应力的影响；车速为20～50 km/h 时，车速变化对冲击系数影响较小，但车速超过50 km/h时，车速的影响逐渐增大；车辆质量对桥梁各项指标动力响应的峰值曲线呈线性增大趋势.当车辆质量为2.80×104 kg，车速30 km/h 时，最大跨中竖向位移为167 mm，未超过抢修桥梁位移限值（L/120），表明该桥梁的设计可以满足抢险的通行要求.

关键词：  纤维增强复合材料桁架桥； 车桥耦合； 位移接触法； 动态响应； 路面不平顺

中图分类号： TU323.4  文献标志码：  A  文章编号：   1671-7775（2024）03-0346-08

引文格式：  孙泽阳，刘  阳，杨俊锋，等. 抢险车对92 m跨度复合材料桁架桥动态响应的影響［J］.江苏大学学报（自然科学版），2024，45（3）：346-353.

收稿日期：   2022-01-23

基金项目：  国家自然科学基金资助项目（52178120）； 中央高校基本科研业务费资助项目（2242022k30030）

作者简介：   孙泽阳（1984—），男，江苏连云港人，博士，副教授，博士生导师（sunzeyang@seu.edu.cn），主要从事新型材料及结构韧性提升技术研究.

刘  阳（2001—），男，浙江宁波人，硕士研究生（1156151590@qq.com），主要从事复合材料在土木工程中的应用研究.

Influence of emergency vehicle on dynamic response of

92 m span composite truss bridge

SUN Zeyang1， LIU Yang1， YANG Junfeng2， WU Bitao3， ZHAO Qilin4

（1. Key Laboratory of Concrete and Pre-stressed Concrete Structures of Ministry of Education， Southeast University， Nanjing， Jiangsu 211189， China; 2. Guangzhou Metro Design and Research Institute Co.， Ltd.， Guangzhou， Guangdong 510010， China; 3. State Key Laboratory of Rail Transit Infrastructure Performance Monitoring and Support， East China Jiaotong University， Nanchang， Jiangxi 330013， China; 4. School of Mechanical and Power Engineering， Nanjing Tech University， Nanjing， Jiangsu 211816， China）

Abstract： To investigate the dynamic performance of long-span truss fiber reinforced polymer（FRP） bridge after repairing completion， the 92-meter-span FRP truss bridge model was established based on guide girder pushing. The vehicle-bridge coupling algorithm of long-span composite truss bridge was compiled to analyze the effects of speed， vehicle weight and road surface roughness on the mid-span vertical displacement， vertical acceleration and key member stress of the FRP truss bridge. The results show that the more uneven the road surface is， the greater the impact of the vehicle on the bridge structure is. The vertical displacement is more affected by the road surface level than that by the member stress. In the speed range from 20 km/h to 50 km/h， the impact coefficient is less affected by the speed change. When the vehicle speed exceeds 50 km/h， the influence of speed change on the impact coefficient is gradually increased. The peak curve of vehicle mass to bridge dynamic response shows linear increasing trend. When the vehicle mass is 2.80×104 kg with vehicle speed of 30 km/h， the maximum mid-span vertical displacement is 167 mm， which does not exceed the military emergency bridge displacement limit （L/120）， indicating that the bridge design can meet the emergency traffic requirements.

Key words：  fiber reinforced polymer truss bridge; vehicle-bridge coupling; displacement contact method; dynamic response; road surface roughness

快速搶修桥梁的安全防护以及应急救援技术是为了应对自然灾害中桥梁的破坏而逐渐发展起来的.抢修桥梁主要包括20世纪90年代设计、建成的跨径51 m的GQL230型重型桁架桥［1］、中型桁架桥、跨径69 m的321装配式公路钢桥、ZB-200公路钢桥等.这几种桥基本是以桁架结构为主的可拆装式钢制桥梁，或采用桥节加强拉杆等结构形式，构件数量多，拼接环节复杂，拼装时间随跨度增加呈现非线性增长，难以满足快速抢险的进程要求.大跨度应急抢修桥梁主要有3种架设方式，即悬臂推出法［2］、骑跨推送法和悬挂推送法.由于抢险条件限制，目前抢修桥梁一般采用人工拼装或人工辅助机械拼装，因而以悬臂推出法为主.

纤维增强复合材料（fiber-reinforced polymer，FRP）轻量化抢修桥梁主要采用适中弹模、高性价比的碳/玻混杂纤维复合材料和铝合金等材料，具有质量轻、承载力高的优点，有利于更好实现拼装部件的模块化，即采用先整体吊装、后平推的先进架设技术，能够大幅度提高架设效率.FRP桁架桥的杆件处于轴向受力状态，因而可充分利用复合材料顺纤维方向强度高的特性［3］.冯鹏等［4］设计了国内第一座FRP桁架桥——茅以升公益桥，该FRP桁架桥具有较高的刚度和承载能力.张冬冬等［5］采用新型结构形式和高性能复合材料制备一座跨度为24 m的轻量模块化应急桥，具有轻质高强、架设方便的特点.赵启林等［6］研究正交异性板与波纹夹芯板两种面板形式的FRP-金属组合桁架结构的力学差异，发现波纹夹芯板具有更好的整体抗弯性能.

拼装桥梁的关键环节是连接技术.徐浏清等［7］对玄武岩纤维（BFRP）桁架桥实例进行建模，确定桁架桥的薄弱节点，从而设计典型K型节点的3种螺栓连接方案.赵启林等［8］提出一种适用于复合材料管的预紧力齿连接技术，该技术充分利用了复合材料层间树脂的黏结作用及金属连接件/复合材料预紧力齿之间摩擦力的共同作用，采用该技术制备了跨径为54 m的复合材料桁架桥.目前，FRP桁架桥已被用作交通应急抢险领域中的应急抢修桥梁.

由于复合材料桥梁质量大大减轻，尤其需要关注抢险通行时的动力性能.车桥耦合振动需要考虑车辆、桥跨结构的动力特性、车速和桥面不平顺等的影响［9］.CAI C. B.等［10］考虑车辆轮胎和桥梁表面的接触关系，将车辆与桥梁系统进行耦合，建议采用隐式建模方法求解车桥耦合振动响应.GUO W. H.等［11］用一辆17自由度四轴车辆动力模型模拟现实中的重型牵引拖车，研究车辆与斜拉桥之间的相互作用.O. HAG-ELSAFI等［12］发现FRP桥面板桥梁相较于相应的混凝土桥梁具有更高的加速度响应.陈云鹤等［13］对FRP桥梁进行车桥耦合动力分析，提出在应急抢修桥通行中应降低车辆速度，以减小跨中位移.综上，随着材料性能和施工工艺的发展，应急抢修桥梁跨径越来越大，结构柔度系数变大后，相应的振动问题就越发突出.应急救援中，短时间内通行重载车辆，且面临各种环境激励，因此应急抢修桥梁动力荷载下振动问题不容忽视.

目前，国内外对于复合材料桥梁车桥耦合动力性能的研究较少，为此，笔者对跨度为92 m的大跨度FRP张弦桁架桥建立精细化数值模型进行车桥耦合动力分析，研究路面不平顺、车辆运行速度以及车身质量对FRP桥梁结构的动力响应，为应急抢修桥梁的设计提供参考.

1  车桥耦合系统模型的建立

1.1  FRP桁架桥基本参数

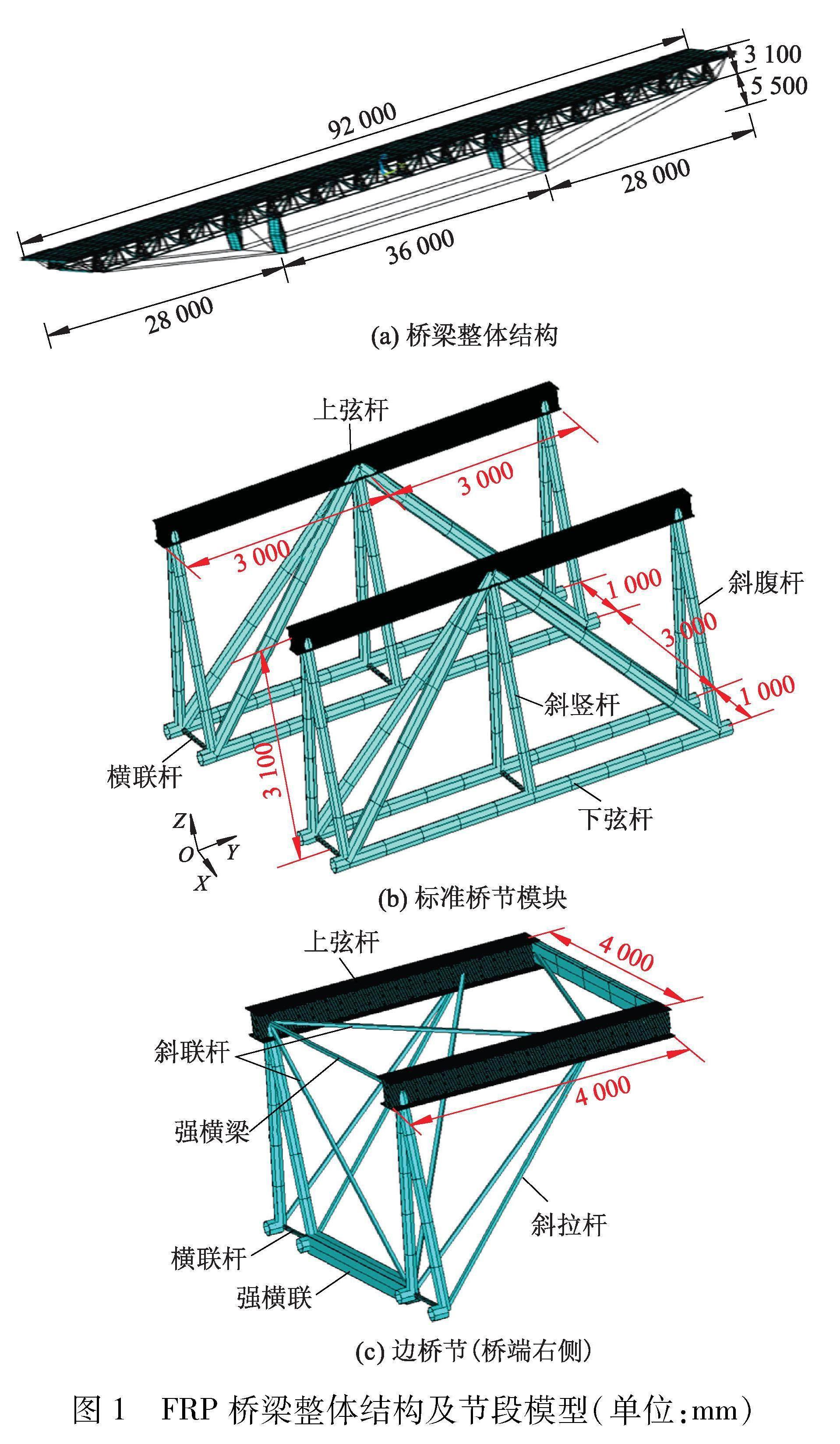
本研究中所用的抢修桥梁整体结构是基于正三角形桁架模块拼装的张弦梁结构，如图1所示.增加张弦系统是为了增加截面抗弯能力，提高桥跨的跨越能力.复合材料杆-铝合金板组合桁架由14节长为6 m的标准桥节和2节长为4 m的边桥节组成，总长为92 m，桥梁总体质量接近3.0×104 kg，相比类似跨度钢桥质量减小40%左右.抢修桥梁的设计可参考这两种桥节，由若干个标准桥节和两个端桥节组成，可以实现其他小跨度桥梁的拼接.

1.2  材料性能

抢修桥梁设计所用材料的性能指标见表1.上弦杆、斜拉杆（边桥节）采用高强钢；标准桥节的斜腹杆、下弦杆采用碳/玻混杂纤维；标准桥节的斜竖杆、边桥节的横联杆采用玻璃纤维；张弦系统拉索采用碳/玻混杂纤维；桥面板材料在保证了刚度要求的情况下为减小其自重而采用铝合金.

采用Beam188梁单元对桥梁杆件进行模拟；对于下部张弦系统拉索，采用Link10软件对其受拉单元进行模拟，通过给单元定义初应变的方式来模拟预拉力；采用Shell181壳单元对桥面板和撑杆单元进行模拟，为了考虑拼装桥面板单独受力时的变形，将桥面板进行分模块化建模.桥节之间采用单、双耳连接，如图2所示，通过节点耦合线位移自由度来释放横桥向转动自由度，模拟其铰接特性.

1.3  车辆动力模型

车辆动力模型采用公路桥梁中常用的空间7自由度双轴模型（见图3），将抢险车分成车体、悬架、轮胎三部分，三者之间用线性弹簧阻尼器连接.

图3中，m1、m2为车体跟桥梁之间接触点的质量；m3、m4为车辆模型前、后轴轮胎的质量；m为车体质量；kt1、kt3、ks2、ks4分别为前、后轴轮胎和前、后轴悬架的刚度；ct1、ct3、cs2、cs4分别为前、后轴轮胎和前、后轴悬架的阻尼；l1、l2为车前、后轴与车体质心的距离；Z1、Z2、Z3、Z4分别为前、后轴4个轮胎的竖向位移；φ为车辆模型俯仰转角；Ip为车辆的俯仰转动惯量.

2  车桥耦合动力分析算法

2.1  路面不平顺的考虑

为增加实际通车过程中的防滑性能，在桥面板上焊接防滑条，以提升行车安全.因此，在原有车桥耦合分析系统中引入路面不平顺激励，研究其对抢修桥动力性能的影响.目前国内外采用的方法主要是现场测试路面不平顺时间历程，或依据功率谱密度函数生成路面不平顺激励样本.根据GB/T 7031—2005《机械振动道路路面谱测量数据报告》规定，路面不平顺位移功率谱密度函数Gq（·）表达式为

Gq（fs）=Gq（f0）fsf0-w，（1）

式中： fs为有效频带中的空间频率；f0为空间参考频率，f0=0.1 m-1；Gq（f0）为当空间频率为f0时的路面功率谱密度，称为路面不平度系数；w为频率指数，一般情况下w=2.

根据GB/T 7031—2005中的相关路面不平顺分级标准，将本研究中的路面划分为A-D级，其路面不平度系数见表2.

表2  路面不平度系数10-6 m3

路面等级下限值几何平均值上限值

A81632

B3264128

C128256512

D5121 0242 048

采用三角级数法，基于Matlab平台编制程序，得到A、B、C和D级路面的随机路面不平顺谱，如图4所示.

2.2  车桥耦合系统运动方程

采用点面接触单元（conta175和targe170）模拟车桥的接触面，通过位移接触法对车辆与桥梁之间耦合作用进行分析［14］.与轮胎节点直接接触的桥面定义为目标面（采用目标单元进行模拟），在接触面与目标面之间设置接触对，建立两者之间的力平衡和位移协调关系，使接触单元与目标单元进行接触运算.通过对接触点单元施加顺桥向位移，从而实现车辆的移动.采用接触力收敛准则来求解车桥系统微分方程，桥梁的动力微分方程［15］如下：

Mbu··

+Cbu·b+Kbub=fb，（2）

式中： u··b、u·b、ub、fb分别为桥梁系统的加速度、速度、位移的向量及车辆作用在桥梁上的荷载矩阵；Mb、Cb、Kb分别为桥梁系统的质量矩阵、阻尼矩阵、刚度矩阵；下标b为桥梁（bridge）.

考虑路面不平順时，车辆与桥面的接触力F计算式为

fb=TNTF=RF，（3）

式中： N为车桥接触点单元形函数矩阵；T为接触单元位置扩展矩阵，其元素由0或1构成；R为接触点位移uc与桥梁节点位移列阵ub的转换矩阵，其中R=TNT.

将所有车轮底下节点作为独立自由度节点，考虑车辆与桥梁的接触和脱离情况，根据达朗贝尔原理，建立车辆模型的车桥耦合系统振动方程：

Mv0

0Mb

z··v

u··b+

Cv00Cbz·v

u·b+

Kv0

0Kb

zv

ub=fgr

RF，（4）

式中： Mv、Cv、Kv分别为车辆系统的质量矩阵、阻尼矩阵和刚度矩阵；zv为简支梁桥强迫振动的动位移函数； fgr为车辆荷载列阵，包括车辆重力、外荷载及每个车轮接触力.

2.3  车桥耦合振动分析算法的验证

为了验证车桥耦合振动分析算法的准确性，将原有车辆模型简化为1/2车辆模型，如图5所示.其中，采用移动弹簧质量模型来模拟车辆，考虑车辆的刚度阻尼，比较其动力性能.简支梁模型跨径为32 m，单位长度的质量为5.41×103 kg/m，抗弯刚度为3.5×1010 N·m2.图5中，ms为车体质量；θ为车辆转角；ks1和ks2分别为后轴和前轴二系弹簧刚度；kt1和kt2分别为后轴和前轴一系弹簧刚度；cs1和cs2分别为后轴和前轴二系弹簧阻尼；ct1和ct2分别为后轴和前轴一系弹簧阻尼；mt1和 mt2分别为后轴和前轴质量；y3、y2、y1分别为车体、前轴和后轴的竖向位移；ρ为简支梁的线密度；EI为简支梁的刚度；a为两轴之间的距离；L为简支梁的长度.

1/2车辆模型前、后轴参数［16］如下：轮对及悬架质量为4.33×103 kg；车轮刚度为4.28×106 N/m；车轮阻尼为9.8×104 kg/s；悬架刚度为2.535×106 N/m；悬架阻尼为1.96×105 kg/s；车体质量为3.85×104 kg；车体转动惯量为2.446×106 kg·m2；车轴距车体质心距离为4.2 m.

采用笔者编写的车桥耦合分析算法，计算不同速度下简支梁跨中竖向位移，结果如图6所示.由图6可知，不同速度v下，文献［16］和本研究的竖向位移曲线均基本吻合，且最大值相差较小，说明该车桥耦合分析方法具有一定的准确性和可信度.

3  车桥耦合作用下的动力性能分析

3.1  路面不平顺的影响

车辆在公路桥梁上行驶时，车辆模型受到路面不平顺激励.通过Matlab软件，采用三角级数法模拟路面不平顺，从而得到路面不平顺对车桥耦合动力响应的影响.路面等级为A-D级和无不平顺，重型抢险车辆的速度为 20 km/h.采用2.1节得到的路面不平顺谱，在5种工况下进行车桥耦合振动分析.重点分析桥梁结构跨中竖向位移、竖向加速度和张弦系统中斜拉索轴向应力的响应时程曲线，以及5种工况对跨中上弦杆、下弦杆、斜拉索轴向应力和冲击系数影响，其中桥梁阻尼比均为0.03.

JTG D60—2015《公路桥涵设计通用规范》中的冲击系数μ计算式为

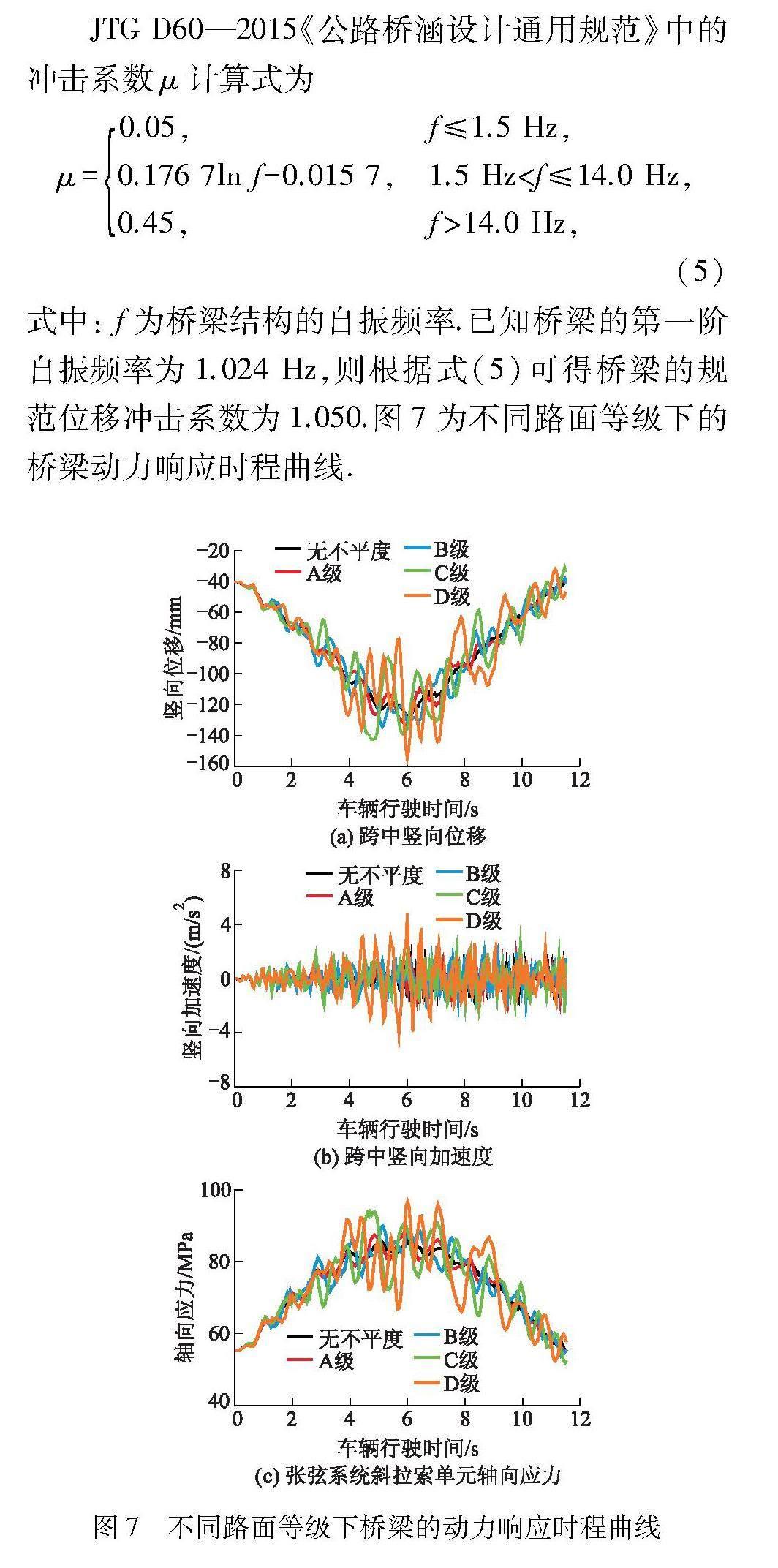
μ=0.05，f≤1.5 Hz，

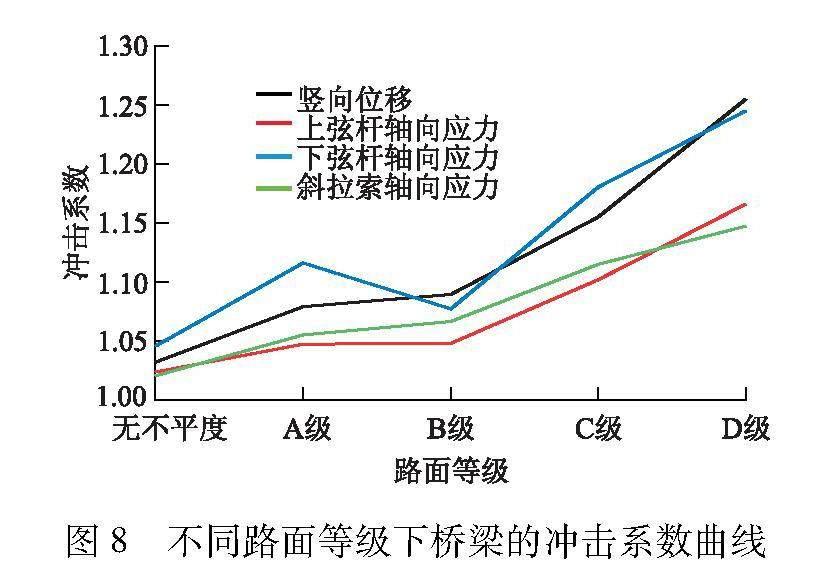
0.176 7ln f-0.015 7，1.5 Hz

0.45，f>14.0 Hz，，（5）

式中： f为桥梁结构的自振频率.已知桥梁的第一阶自振频率为1.024 Hz，则根据式（5）可得桥梁的规范位移冲击系数为1.050.图7为不同路面等级下的桥梁动力响应时程曲线.

由图7可知，考虑路面不平顺激励的曲线振荡幅度及幅值大于不考虑路面不平顺的情况.由于本桥梁是装配拼装式桥梁，桥面板之间分别受力，且受冲击作用较大.故相较于传统桥梁，本桥梁整体变形增大，桥梁跨中竖向位移、竖向加速度和斜拉索轴向应力3个参数会出现明显的波动区间.当路面等级从B级向C级过渡时，联合图4可知，不平顺谱曲线中不平度的增幅较大，故相较于B级路面，其曲线波动幅度以及3个参数的峰值增大.当不考虑路面不平顺时，跨中竖向位移为127 mm.相较无不平度，路面等级为A、B、C和D级时的竖向位移分别增加4.5%、5.6%、12.0%和21.6%；当路面等级为D级时，斜拉索的轴向应力增加12%，可见竖向位移受路面等级的影响远大于杆件应力.因此，实际车辆通行中，应重点考虑路面不平顺对桥梁竖向位移的影响.

图8为不同路面等级下桥梁的冲击系数曲线.

由图8可知：随着路面不平顺等级增加，位移冲击系数逐渐增加，且当路面等级低于B级之后，冲击系数增加明显；不考虑路面不平顺时位移冲击系数为1.030，路面等级为D级时的位移冲击系数最大值为1.250，超过规范冲击系数（1.050）.对于关键杆件，下弦杆的冲击系数大于上弦杆和斜拉索.当路面等级为D级时，下弦杆冲击系数为1.240，而上弦杆和斜拉索的冲击系数分别为1.170和1.150.这是由于上弦杆与桥面板相连，且桥梁的支座约束设置在上弦杆上，其约束强于下弦杆，故冲击作用小于下弦杆.

3.2  车速的影响

为比较不同车速下FRP桁架桥的动力性能，采用B级路面，选择车速v为20、30、40、50和60 km/h，在此工况下研究FRP桁架桥梁跨中节点的竖向位移、关键杆件的轴向应力和冲击系数受到的影响.不同车速下桥梁的动力响应时程曲线如图9所示.由图9可知： 随着速度逐渐增加，跨中竖向位移时程曲线的振荡幅度呈先减小、后增大的趋势，而关键杆件的轴向应力呈先增大、后减小的趋势；当速度从50 km/h增大到60 km/h时，整体动力响应的峰值增幅最大，说明桥梁的动力响应受车辆高速的影响远大于低速.

圖10为不同车速下桥梁跨中位移和关键杆件轴向应力的冲击系数曲线.

由图10可知：跨中位移冲击系数基本随着速度的增加而增大；当车速为20 km/h时，位移冲击系数为1.040，小于规范冲击系数；当速度为50～60 km/h时，冲击系数为1.180；车速为30、40、50和60 km/h时，冲击系数增幅分别为4.7%、-0.3%、4.2%和4.9%，其中60 km/h时的增幅最大.因此，在FRP桥梁上行驶的车辆应限速，车速应不超过50 km/h.由图10还可知：在速度区间为20～50 km/h时，关键杆件冲击系数增加缓慢，受速度变化影响较小；当速度从50 km/h增大到60 km/h时，上弦杆和下弦杆冲击系数变化增大，最大值分别为1.160和1.570.可见，随着车速增大，路面不平度不断增大，导致车辆与桥梁的冲击作用也增大.因而，车辆的高速对桥梁的动力响应远大于低速.

3.3  车身质量的影响

不同质量的车辆对桥梁整体结构会产生不同的惯性力.FRP 拼装式桁架桥整体结构刚度小，质量轻，而应急抢险领域中的抢险车质量一般为1.50×104～3.00×104 kg.为研究车身质量对FRP桁架桥动态性能的影响，选取总质量为1.8×104～2.6×104 kg的车辆为研究对象，车速均为30 km/h，路面等级为B级.图11为不同车身质量m下桥梁的动力响应时程曲线.由图11可知：质量较大的车辆对FRP桁架桥动力响应影响较大，桥梁结构各动力响应峰值随着质量的增加而增大，且杆件应力曲线的振荡幅度趋于增大；当车辆模型到达桥梁跨中位置之前，由于车辆向上爬坡，桥梁振动加剧，且3个参数的波动幅度逐渐增加.

图12为不同车身质量下的冲击系数曲线.

根据车辆固有频率表达式fg=12π km可知，随着车身质量的增加，车辆模型的固有频率逐渐减小，并逐渐靠近桥梁的基频.因此，由图12可知，随着车身质量的增加，位移冲击系数逐渐增大，但增幅都不大，最大位移冲击系数仅为1.110，均小于路面不平顺及车速的最大位移冲击系数（1.250和1.180），因此说明车身质量对位移冲击系数的影响小于路面不平顺及车速的影响.由图12还可知，上弦杆轴向应力冲击系数呈先减小、后增大的趋势，最大冲击系数为1.063；斜拉索呈先增大、再减小、后增大的趋势，最大冲击系数为1.075；下弦杆呈不断增加的趋势，最大冲击系数为1.088.可见，下弦杆最大冲击系数大于上弦杆和斜拉索，因而下弦杆冲击系数受车身质量影响最大.对于峰值响应，其最大竖向位移（167 mm）和最大杆件轴向应力（126.4 MPa）分别小于规范中的竖向位移限值（L/120）和材料的极限强度，说明该桥梁结构满足设计要求.

4  结  论

1） 路面不平顺等级对桥梁各项动力响应都有较大影响，路面越不平顺，车辆与桥梁结构之间的冲击振动作用更大.当路面等级从A级过渡到D级，竖向位移增加21.6%，跨中上弦杆、下弦杆和斜拉索轴向应力分别增加14%、19%和12%，因而竖向位移受路面等级的影响远大于杆件应力.实际通行中，应重点考虑路面不平顺对桥梁竖向位移的影响.

2） 随着车速逐渐增加，竖向位移、竖向加速度及轴向应力均呈增加趋势，且由于铝合金桥面板之间单独受力，冲击动力响应受车速影响更大，其中下弦杆应力受速度变化影响最大.速度区间为20～50 km/h时冲击系数平稳增加，受速度变化影响较小.当车速超过50 km/h后，冲击系数受速度变化影响增大，冲击效应增大，应对车速进行适当控制.

3） 桥梁各项动力响应的峰值随着车身质量的增加呈线性增大趋势.动力响应的最大竖向位移（167 mm）和最大杆件轴向应力（126.4 MPa）分别小于规范中的竖向位移限值（L/120）和材料的极限强度，说明该FRP桁架桥结构刚度达标，相比钢桥质量减小了40%左右.在满足应急桥梁变形的要求下，FRP桥梁的架设效率远大于钢桥，桥梁设计满足抢修通行要求.

[WT5HZ]参考文献（References）[WT5”BZ]

［1］  张宏建，潘大荣，赵栋，等. 大跨公路应急救援桥主结构形式与架设技术研究［J］. 国防交通工程与技术， 2019，17（5）：1-5.

ZHANG H J， PAN D R， ZHAO D， et al.On the structural formation of the main structure of a long-span highway emergency bridge and its erection technology［J］. Traffic Engineering and Technology for National Defence， 2019，17（5）：1-5.（in Chinese）

［2］  李驰，吴美君. 悬臂推出法架设大跨径装配式公路钢桥施工技术［J］. 湖南交通科技， 2013，39（3）：127-131.

LI C，WU M J. Construction technology of long-span prefabricated highway steel bridge by cantilever push-out method［J］.Hunan Transportation Science and Technology， 2013，39（3）：127-131.（in Chinese）

［3］  赵启林，高建岗，陶杰，等. 复合材料桁架桥的若干关键问题探讨［J］. 南京工业大学学报（自然科学版）， 2017，39（5）：146-152.

ZHAO Q L，GAO J G，TAO J， et al. Present situation and problems of design and calculation of hybrid FＲP-steel truss bridge［J］. Journal of Nanjing Tech University（Natural Science Edition）， 2017，39 （5）：146-152.（in Chinese）

［4］  冯鹏，田野，覃兆平. 纤维增强复合材料拉挤型材桁架桥静动力性能研究［J］. 工业建筑， 2013，43（6）：36-41.

FENG P，TIAN Y，QIN Z P. Static and dynamic behavior of a truss bridge made of FRP pultruded profiles［J］. Industrial Construction， 2013，43（6）：36-41.（in Chinese）

［5］  张冬冬，袁嘉欣，赵启林，等. 新型纤维增强复材-金属组合空间桁架结构及弯曲性能研究［J］. 工业建筑， 2019，49（9）：102-108，166.

ZHANG D D，YUAN J X，ZHAO Q L，et al. A novel FRP-metal space truss structure and its flexural perfor-mance［J］. Industrial Construction， 2019，49（9）：102-108，166.（in Chinese）

［6］  赵启林，刘鹏飞，徐龙星，等. 玻璃纤维复合材料-钢组合桁架结构长期力学性能研究［J］.工业建筑， 2013，43（增刊）：210-214.

ZHAO Q L， LIU P F，XU L X，et al. Research on mechanical properties of a glass fiber reinforced polymer-steel combined truss structure［J］. Industrial Construction， 2013，43（Sup）：210-214.（in Chinese）

［7］  徐瀏清，梁梦蝶，江镇，等.多轴向BFRP方管桁架K型节点性能分析［J］.南京工业大学学报（自然科学版），2023，45（1）：71-78.

XU L Q， LIANG M D， JIANG Z， et al. Performance analysis of K-type joints of multi-axial BFRP square tube truss［J］. Journal of Nanjing Tech University （Natural Science Edition）， 2023，45（1）：71-78.（in Chinese）

［8］  赵启林，高一峰，李飞. 复合材料预紧力齿连接技术研究现状与进展［J］. 玻璃钢/复合材料， 2014（12）：52-56.

ZHAO Q L， GAO Y F， LI F. Current research and development of the application of the pre-tightened tooth connection［J］. Fiber Reinforced Plastics/Composites， 2014（12）：52-56.（in Chinese）

［9］  GOU H Y， SHI X Y， ZHOU W， et al. Dynamic performance of continuous railway bridges： numerical analyses and field tests［J］. Journal of Rail and Rapid Transit， 2018，232（3）：936-955.

［10］  CAI C B， HE Q L， ZHU S Y， et al. Dynamic interaction of suspension-type monorail vehicle and bridge： numerical simulation and experiment［J］. Mechanical Systems and Signal Processing， 2019，118：388-407.

［11］  GUO W H， XU Y L. Fully computerized approach to study cable-stayed bridge-vehicle interaction［J］. Journal of Sound and Vibration， 2001，248（4）：745-761.

［12］  HAG-ELSAFI O，ALBERS W F，ALAMPALLI S. Dynamic analysis of the bentley creek bridge with FRP deck［J］. Journal of Bridge Engineering， 2012，17（2）：318-333.

［13］  陈云鹤，李师桢，张广友，等. 一种FRP轻便桥主梁的动力性能研究［J］. 国防交通工程与技术， 2014，12（2）：7-11，24.

CHEN Y H， LI S Z， ZHANG G Y， et al. A theoretical study of the dynamic performance of the main girder of an FRP light bridge［J］.Traffic Engineering and Technology for National Defence， 2014，12（2）：7-11，24.（in Chinese）

［14］  陈一铂. 移动体系与结构相互作用分析及ANSYS实现［D］. 石家庄：石家庄铁道大学， 2015.

［15］  周瑞娇，王艳，陈淮.在役大跨径曲弦桁梁桥车桥耦合振动分析［J］.振动工程学报，2022，35（1）：103-112.

ZHOU R J， WANG Y， CHEN H.Analysis of vehicle-bridge coupled vibration of long-span curved truss bridge in service［J］. Journal of Vibration Engineering， 2022，35（1）：103-112.（in Chinese）

［16］  沈火明，肖新標. 求解车桥耦合振动问题的一种数值方法［J］. 西南交通大学学报， 2003，38（6）：658-662.

SHEN H M， XIAO X B. Numerical method for vehicle-bridge coupled vibrations［J］. Journal of Southwest Jiaotong University， 2003，38（6）：658-662.（in Chinese）

（责任编辑  赵  鸥）