障碍干扰下的压缩感知电磁成像算法

周炽 杨春夏

摘  要： 基于电磁成像模型，针对逆散射问题的病态性和非线性性质，引入压缩感知（CS）中的全变分（TV）算法，旨在减少所需天线数量，并提高电磁成像的图像质量.在玻恩（Born）迭代的基础上，引入全变分压缩感知算法（TV-CS）. 仿真结果显示：即使目标被障碍物遮挡，该算法也能够在配置较少探测天线的情况下，对目标位置和形状进行准确的重构.

关键词： 电磁逆散射； 压缩感知（CS）； Born迭代； 全变分（TV）算法

中图分类号： TP 391.4    文献标志码： A    文章编号： 1000-5137（2024）02-0268-05

Compressive sensing electromagnetic imaging algorithm in the presence of obstacle interference

ZHOU Chi， YANG Chunxia^*

（College of Information，Mechanical and Electrical Engineering，Shanghai Normal University，Shanghai 201418，China）

Abstract： Based on the electromagnetic imaging model， the ill-posed and nonlinear nature of the inverse scattering problem was addressed by introducing the total variation （TV） algorithm in compressive sensing （CS） to reduce the required number of antennas and to enhance the image quality of electromagnetic imaging. Building upon the Born iteration， the total variation compressive sensing （TV-CS）algorithm was introduced. Simulation results demonstrated that this algorithm could achieve more accurate reconstruction of target position and shape with fewer deployed antennas， even in scenarios where the target was obscured

Key words： electromagnetic inverse scattering； compressive sensing （CS）； Born iteration； total variation （TV） algorithm

电磁逆散射是通过分析已知的入射场和散射场，来重构出目标散射体的几何和物理特性，包括位置、对比度、形状大小以及数量等信息. 由于解不唯一和多重散射效应，电磁逆散射问题是一个非线性、病态的问题. 为了克服电磁逆散射的非线性，对于弱散射体，可以采用线性近似的方法，例如：玻恩（Born）近似^［1］方法和里托夫（Rytov）近似^［2］方法. 对于强散射体，可以采用迭代方法，例如：玻恩迭代法^［3］（BIM）和变形玻恩迭代法^［4］（DBIM）.此外，可以引入附加信息，通过正则化方法来改善病态问题的不稳定性，常见的正则化技术包括Tikhonov正则化^［5］和全变分（TV）正则化^［6］.

压缩感知（CS）是一种信号处理技术，可以从远少于香农-奈奎斯特采样定理^［7］所需的样本数中恢复特定信号，这使其在信号处理相关领域，包括电磁成像问题中获得了广泛的应用. CS不需要设置大量天线来克服逆散射问题中的病态性，仅依赖于相对较少的观测点信息，就能够实现对目标散射体的压缩成像. CS依赖于两个条件：稀疏性及不相关性. 在电磁成像中，如果成像区域中的目标是小散射体且具有良好的稀疏性，CS能够很好地求解目标散射体. 对于求解大散射體，目标散射体在成像区域不具有稀疏性，不能直接使用CS进行求解，需通过间接稀疏先验制定反演算法.

本文作者提出基于全变分压缩感知（TV-CS）的电磁反演策略，在求解大尺度散射目标时，将散射体的梯度域作为稀疏域，可大大减少天线配置数量，降低计算复杂度，并且在处理障碍物遮挡环境下的成像问题时表现出良好的性能.

1  成像模型

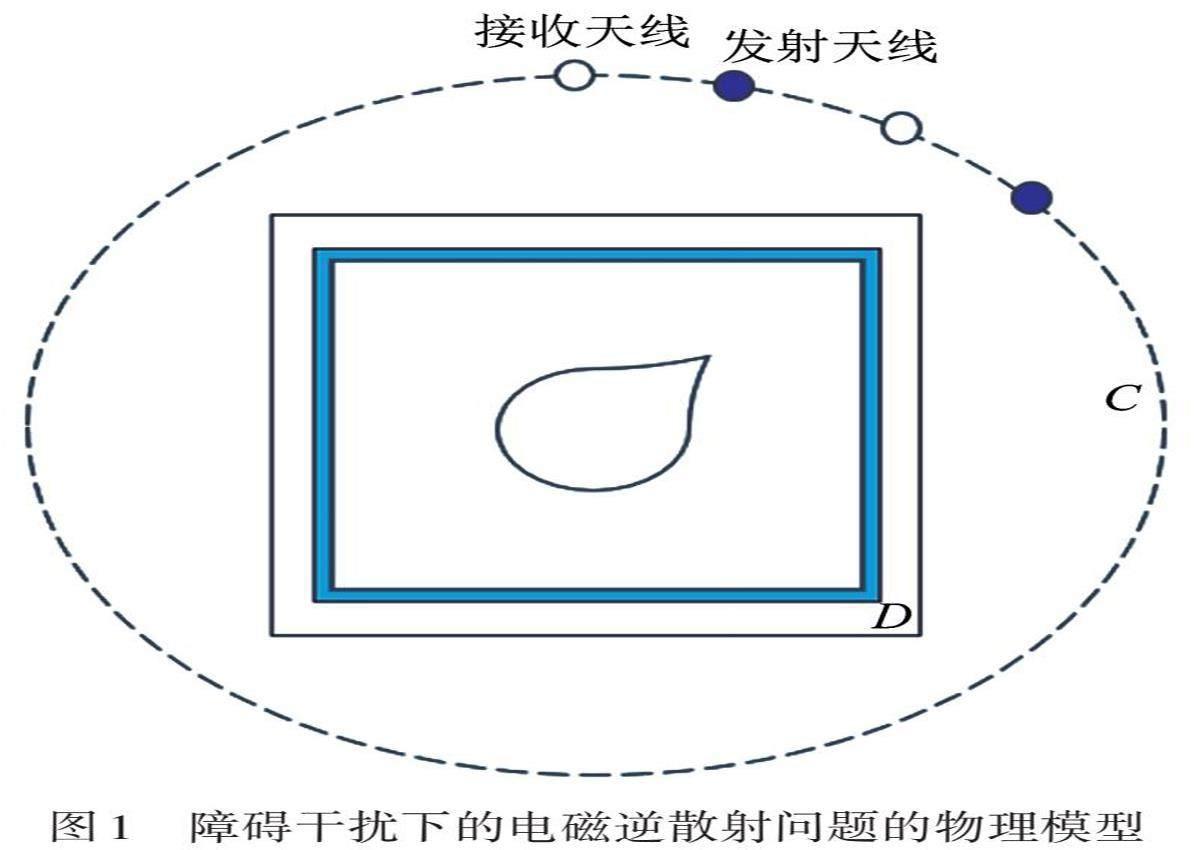
障碍干扰下的电磁逆散射问题的物理模型如图1所示，假设在自由空间中有一个均匀背景介质的成像区域D，其内部分布着待测的散射体，障碍物围绕在散射体四周，信息未知，发射和接收电磁波的发射天线和接收天线位于成像区域D之外的观察区域C中. 当被电磁波照射到时，散射体产生散射场，其与入射场叠加的总场被接收天线所接收，根据在接收点测得的散射数据，计算成像区域D内散射体的形状、位置和材料.

对于二维问题，在观测区域C中，测量的散射场满足：

（1）

其中，和分别为散射场和总场；是坐标矢量；为背景介质中的波数；是二维自由空间格林函数；（·）是对比度函数，

， （2）

其中，是相对介电常数；是电导率；是均匀无损背景的介电常数；f为入射波频率.

将待求的对比度函数离散化表示为分段常数函数

（3）

其中，代表坐標是脉冲基函数.

将式（3）代入式（1），可以得到目标散射体的CS模型：

（4）

其中，

（5）

（6）

2  TV算法

在图像恢复方面，有研究已经证实，在CS问题中使用TV正则化可以更准确地保留边缘或边界，使所恢复图像的质量更加清晰，这对于表征图像至关重要. TV正则化的优势在于不仅可以恢复稀疏信号或图像，还可以恢复密集的阶梯信号或分段常数图像.

对于稀疏的对比度函数梯度，用CS的TV正则化方法求解，

， （7）

其中，为对比度梯度. 由于是不可微和非线性的，式（7）是不光滑的，很难直接求解. 引入辅助变量

（8）

根据增广拉格朗日算法^［8］，将式（7）改写为：

（9）

其中，（·）表示增广拉格朗日函数和表示拉格朗日乘子向量和表示惩罚系数.

式（9）为增广拉格朗日函数下电磁逆散射的求解模型，对于求解式中的和，可以使用交替方向乘子法（ADMM）^［9］分別求解.

3  实验与分析

本实验中，D是自由空间中边长为2 m的正方形区域，将其划分成50×50的像素网格，设置成像区域的中心为坐标原点，并将该区域内的背景相对介电常数设定为1. 障碍物是一座矩形墙体，外边长为1.8 m，厚度为0.04 m，对比度为0.5. 待测目标是被墙体包围的一个圆形散射体，半径为0.25 m，对比度为1. 成像区域外的观察区域中，以坐标原点为圆心，10 m为半径，等间距排列12根发射天线和12根接收天线，入射波的频率为0.4 GHz.

实验采用结合Born迭代的方法，对较高对比度目标进行成像. 在第一次迭代时，采用一阶Born近似，将入射场近似作为总场，测量方程近似为关于对比度的线性方程，可以利用TV-CS求解对比度；根据上一轮得到的对比度计算总场，反复迭代逼近真实目标对比度. 由于障碍物信息是未知的，将其视为目标的一部分. 为了验证算法的成像效果，将仿真结果与衍射层析成像（DT）算法^［10］和子空间优化（SOM）算法^［11］的结果作对比. DT算法是一种基于傅里叶变换的线性近似反演算法，SOM算法是基于奇异值分解（SVD）^［12］的迭代优化反演算法.

图2展示了三种算法对在障碍干扰下的散射体的重构结果. 由图2可知：当散射体对比度较大时，DT算法仅能够重构出散射体的基本轮廓，不能精确地重构出散射体的对比度；SOM算法基本能够重构出散射体的形状和对比度，但边缘细节比较模糊；基于Born迭代近似的TV-CS方法综合了Born迭代近似和增广拉格朗日TV算法的优点，弥补了其他算法的不足，重构效果最佳.

4  结语

本文作者结合Born迭代近似算法和TV算法求解电磁逆散射问题，将未知散射体的离散梯度作为先验信息，对散射体的信息进行重构. 实验结果表明，在散射体被障碍干扰的情况下，基于Born迭代的TV-CS算法能够准确地重建出目标散射体的对比度、形状和位置，尤其对于具有边缘细节的散射体，具有较强的稳健性.与传统算法相比，使用TV-CS算法，仅需少量天线就可以较好地恢复目标散射体.

参考文献：

［1］ HUDSON J A， HERITAGE J R. The use of the Born approximation in seismic scattering problems ［J］. Geophysical Journal International， 1981，66（1）：221-240.

［2］ DEVANEY A J. Inverse-scattering theory within the Rytov approximation ［J］. Optics Letters， 1981，6（8）：374-376.

［3］ WANG Y M， CHEW W C. An iterative solution of the two‐dimensional electromagnetic inverse scattering problem ［J］. International Journal of Imaging Systems and Technology， 1989，1（1）：100-108.

［4］ CHEN X. Computational Methods for Electromagnetic Inverse Scattering ［M］. New York： John Wiley & Sons， 2018.

［5］ GOLUB G H， HANSEN P C， O'LEARY D P. Tikhonov regularization and total least squares ［J］. SIAM Journal on Matrix Analysis and Applications， 1999，21（1）：185-194.

［6］ LI C B. An efficient algorithm for total variation regularization with applications to the single pixel camera and compressive sensing ［D］. Texas：Rice University， 2010.

［7］ LUKE H D. The origins of the sampling theorem ［J］. IEEE Communications Magazine， 1999，37（4）：106-108.

［8］ OLIVERI G， ANSELMI N， MASSA A. Compressive sensing imaging of non-sparse 2D scatterers by a total-variation approach within the Born approximation ［J］. IEEE Transactions on Antennas and Propagation， 2014，62（10）：5157-5170.

［9］ GLOWINSKI R， LE TALLEC P. Augmented Lagrangianand Operator-Splitting Methods in Nonlinear Mechanics ［M］.Philadelphia： Society for Industrial and Applied Mathematics， 1989.

［10］ BOYD S， PARIKH N， CHU E， et al. Distributed optimization and statistical learning via the alternating direction method of multipliers ［J］. Foundations and Trends in Machine learning， 2011，3（1）：1-122.

［11］ DEVANEY A J. Geophysical diffraction tomography ［J］. IEEE Transactions on Geoscience and Remote Sensing， 1984（1）： 3-13.

［12］ MICHAEL E W， RECHTSTEINER A， ROCHA L M. Singular value decomposition and principal component analysis ［J/OL］. arXiv： physics/0208101v4，2002 ［2023-12-01］. https： //arxiv.org/abs/physics/0208101v4.

（責任编辑：包震宇，顾浩然）

DOI： 10.3969/J.ISSN.1000-5137.2024.02.019

收稿日期： 2023-12-23

基金项目： 国家自然科学基金（61801293）

作者简介： 周炽（2000—）， 男， 硕士研究生， 主要从事电磁场与微波技术方面的研究. E-mail： 1000528179@smail.shnu.edu.cn

* 通信作者： 杨春夏（1988—）， 女， 副教授， 主要从事电磁场与微波技术方面的研究. E-mail： chunxiay@shnu.edu.cn

引用格式： 周炽， 杨春夏. 障碍干扰下的压缩感知电磁成像算法 ［J］. 上海师范大学学报 （自然科学版中英文）， 2024，53（2）：268?272.

Citation format： ZHOU  C， YANG C X. Compressive sensing electromagnetic imaging algorithm in the presence of obstacle interference ［J］. Journal of Shanghai Normal University （Natural Sciences）， 2024，53（2）：268?272.