房价波动会抑制全要素生产率增长吗？

李嘉琪 陈妍玲 郭文伟

摘   要：在阐明房价波动对全要素生产率的影响机理后，采用F？覿re-promont指数法测度我国259个地级及以上城市全要素生产率及其分解指标，然后采用空间面板模型分析房价波动对全要素生产率的影响及具体路径。研究结论表明，在全国范围内，房价波动会直接对全要素生产率生产明显的抑制作用，也会通过降低规模效率来间接抑制全要素生产率；这种抑制作用不仅作用于本市，还会通过空间溢出效应对邻市产生影响；东部、中部、西部和东北地区房价波动均显著抑制全要素生产率增长但各自的影响途径存在明显差异，中部地区房价波动的抑制作用不存在空间溢出效应；政府财政独立性和外商投资无助于提升全要素生产率。

关键词：房价波动；F？覿re-promont指数法；技术效率；规模效率；剩余混合效率；空间滞后模型；空间误差模型

DOI：10.3969/j.issn.1003-9031.2024.05.001

中图分类号：F830              文献标识码：A     文章编号：1003－9031（2024）05－0003－19

一、引言

全要素生产率（total factor productivity，TFP）是指在生产过程中，除了生产要素投入之外的科技进步对经济增长贡献的因素（易纲等，2003），能刻画由规模增长模式向创新驱动经济增长模式的转变程度。当前，我国企业的人口红利和资源红利等传统优势正在趋于消失，数量型扩张的经济模式已难以为继，在经济新常态下，中国要保持经济平稳较快可持续发展，就必须重视全要素生产率的提升。然而，我国全要素生产率自2008年金融危机后出现持续下滑，直到2016年，我国全要素生产率增速才出现由降转升的拐点，但至今我国的科技发展水平和资源配置效率仍与发达国家存在较大差距。Denison and Dward（1962）将牵制全要素生产率的原因归为知识进步、规模经济和资源配置效率改善三大因素。因此要提高整体的生产率水平，硬性的技术进步是十分重要的，但资源配置效率改善带来的作用也不可忽视；而在优化资源配置效率方面，房价波动是不容忽视的重要因素之一。当前中国房价增速较快，2007年中国住宅均价为3645.18元/平方米，2020年这一指标首次突破万元大关，达到10158.94元/平方米，同比上涨了178.70%①。高房价加剧了我国经济的结构失衡，导致整个社会资源过度集中在房地产领域，最终降低了资源再配置效率，抑制了全要素生产率增长。因此，从理论和实践上揭示我国房价波动对全要素生产率增长的机理、路径，进而提出缓解高房价抑制全要素生产率的政策建议，具有重要意义。本文首先通过F？覿re-promont指数法合理测算我国259个地级市全要素生产率的变化趋势并进行成分分解；在此基础上，采用面板数据模型和空间面板模型分析房价波动对于全要素生产率的影响路径，包括技术效率路径、规模效率路径和剩余混合效率路径；其次分别比较了我国东部、中部、西部和东北地区房价波动对全要素生产率及其影响路径的差异。最终研究结果发现，全国层面上房价波动会通过影响规模效率来显著抑制全要素生产率增长，且这种抑制作用不仅作用于本市，还会通过空间溢出效应对邻市产生影响；与此同时，东部、中部、西部和东北地区房价波动抑制全要素生产率增长的路径存在明显差异。

二、文献综述

（一）全要素生产率的测度

当前学术界关于全要素生产率主要有5种测算方法：索洛余值法、随机前沿分析（SFA）法、DEA-Malmquist指数法、Hicks-Moorsteen指数法和F？覿re-promont指数法。索洛余值法是通过拟定生产函数后得到的產出增长率扣除各生产要素增长率后的残差。该方法简便易算，但其前提条件过于严格，如技术进步外生、技术进步不改变生产要素投入比例以及规模收益不变等。尽管后来学者修正了其生产要素的测度以及技术进步的外生性问题，但其认为规模收益不变的不合理假设依旧存在。SFA法将总生产函数分为非效率的和前沿的（Chen and Guan，2012），对全要素生产率进行了拆解，将其变化拆分为技术进步和技术效率并最终计算出该指标（Aigner et al.，1977；Kumbhaka，2000）。该方法承认技术无效率的情况，更符合现实。但局限性在于仅能计算单项产出时的全要素生产率；此外，基于小样本数据的随机前沿生产函数法估计结果差异较大。DEA-Malmquist指数法是一种非参数测度方法（Charnes et al.，1978；颜鹏飞和王兵，2004；徐晔和宋晓薇，2016；焦翠红和陈钰芬，2018）。该方法无须考虑被估计的生产函数形态和要素价格信息，突破了以往仅能测算单项产出的局限。此外，该方法认为技术效率可以由规模效率和纯技术效率两个部分组成，因而更贴合社会生产实际情况，具有更强的适用性；但存在着乘法完备性较差以及效率分解不全面的问题（Bjurek，1996），对异常数据反应敏感，易受随机因素影响导致得到的技术进步和技术效率指数出现误差。O donnell（2008）最先提出Hicks-Moorsteen TFP指数法，该学者解决了全要素生产率变化分解的不全面的问题，并使得分解指数的经济含义更为清晰明确，遗憾的是，该测量方法无法实现传递性检验（刘秉镰等，2012；姜永宏和蒋伟杰，2014；刘宏伟等，2017）。F？覿re-primont指数法也是O donnell（2012）提出的，是目前国际上最新的测度方法，该指数具有乘法完备性，且效率分解完全，FP指数可以对全要素生产率进行纵向和横向两个方向的比较（郭萍等，2013；黄祎等，2015）。

（二）房价波动影响全要素生产率的路径研究

至今国内外较少有关房价波动与全要素生产率之间关联性方面的研究文献，大部分文献集中研究房价波动如何通过影响资源配置效率和科技创新水平进而影响全要素生产率的问题。在高房价影响资源配置效率方面，郭庆旺和贾俊雪（2005）、Hsieh and Klenow（2009）认为当资源集中于低生产率企业时，将会导致资源配置在市场中分配失衡，产品和生产要素市场扭曲，最终抑制全要素生产率的提高。陈斌开等（2015）、徐晔和宋晓薇（2016）指出过高的楼市价格对社会消费和投资形成挤出效应，使得有限资源流向低外部性的房地产业，也吸引不少工业企业偏离自身主业发展而开始涉入房地产业，从而进一步加剧了社会资源的错配并降低了资源配置效率。Restuccia et al.（2008）认为高房价带来的社会资源配置失效将会显著降低全要素生产率。此外，朱喜等（2011）、Robert et al.（2014）通过实证表明，当这种资本和劳动配置的扭曲被修正时，全要素生产率将得到显著的提升。

在房价波动影响科技创新水平方面，部分学者认为当社会资源过度集中到房地产部门时，这不仅抑制了高新企业自身的研发投入积极性，也加重了实体经济部门的生产成本，挤占了创新研发资金来源（王文春等，2014；Miao and Wang，2014）；这种挤出效应将对整个行业全要素生产率产生抑制作用（余静文，2017）。大多数学者的研究结论表明高房价对企业创新投入和对劳动力的挤出削弱企业的创新倾向并抑制了城市的创新能力（朱晨，2018）。在科技创新对全要素生产率的影响方面，学者们还没有得出统一的结论，部分学者认为科技创新水平的提高能够促进全要素生产率（刘康，2024；陈彦君和郭根龙，2024）：一方面，创新资本投入本身能够显著提升科技水平并促进全要素生产率（魏下海和王岳龙，2010），高新科技开发区的全要素生产率显著高于其他地区（程郁和陈雪，2013）；另一方面，创新资本的投入又聚集了大量的科研人才，这种集聚有利于新知识和新技术的扩散，科技人员的流动进一步促进了创新和全要素生产率（焦翠红和陈钰芬，2018）。然而，也有部分学者得出相反的结论，认为创新资本对全要素生产率的促进作用受到地区经济、要素禀赋和制度环境等条件的限制（余泳泽和张先轸，2015）；在经济发展水平较低的情况下，创新资本对我国全要素生产率的促进作用并不明显，甚至抑制了地区全要素生产率的增长（杨剑波，2009；吴敏洁等，2018）。

综上所述，目前学界在研究房价波动是否会影响全要素生产率这一领域存在如下不足：一是研究视角的局限。研究房价水平对科技创新或资源配置效率的影响较为集中，直接研究房价波动对全要素生产率的影响较少；二是关于房价波动影响全要素生产率的影响路径分析不够充分。总体上看，多数文献仅研究了房价波动对于资源配置效率和科技创新水平所带来的影响，没有进一步拓展到全要素生产率的层面，同时也没有区分我国不同地区房价波动对区域全要素生产率的影响差异。对此，本文将首先采用F？覿re-primont指数法合理测算我国259个地级及以上城市的全要素生产率（TFP），并将TFP变化拆分为技术进步、技术效率、规模效率和剩余混合效率，以进一步探讨房价波动影响全要素生产率的具体路径。此外，从宏观经济环境、城市创新能力等维度来系统探究影响我国全要素生产率的核心因素；结合全国259个地级及以上城市数据搭建房价波动—全要素生产率的实证模型，不仅从时间和空间两个维度进行研究，而且区分了全国和东部、中部、西部、东北地区两个层面来展开实证。本文的研究特色在于：一是全面系统的研究对象。在我国293个地级及以上城市中，本文在考虑了数据的可得性基础上选择了尽可能多的研究对象，最后挑选共259个地级及以上城市，避免了现有研究以局部地区或少数城市为研究对象而缺乏代表性的问题；二是研究方法的创新。大部分文献分析房价对产业结构升级的影响机制时，运用的是时间序列或面板模型。这一方面忽视了房价波动对全要素生产率的非线性影响特征；另一方面，也无法进一步揭示房价波动影响全要素生产率的具体路径。对此，本文在合理测算全要素生产率并将其分解为技术效率、规模效率和剩余混合效率这三个效率指标的基础上，先从时间维度揭示房价波动影响全要素生产率的具体路径，进而从空间维度探索房价波动对全要素生产率的空间溢出效应，最后比较我国不同地区之间房价对全要素生产率的影响差异性。

三、理论分析与研究假设

全要素生产率增长一般表现为知识进步、规模经济和资源配置效率改善等三个方面（Denison，1962）。F？覿re-promont指数法作为较新的测算方法，可将该指标分解为技术效率、规模效率和剩余混合效率，与该指标的外在表现形式基本一致。技术效率是纯粹技术进步对产出效率的贡献；规模经济是指生产过程中，扩大投入所引起的产出增加，且产出增加的规模要大于要素投入的规模；剩余混合效率则考察具有技术效率的生产单位通过改变产出组合所引起的全要素生产率变化（郭萍等，2013）。房地产价格波动可能通过影响技术效率、规模效率和剩余混合效率进而影响全要素生产率。内生经济增长理论认为，技术进步是由内生决定的，国家之间的经济发展差距可以通过技术外部性和资本积累实现，技术进步还受制于创新研究能力。但过往我国房地产行业有着高回报、低风险特点，加上房价保持增长，导致企业改变原投资结构，挤出了研究创新方面的投入（朱晨，2018）。因此，本文提出研究假设1：房价波动会抑制全要素生产率增长；研究假设2：房价波动会通过降低技术效率進而抑制全要素生产率增长。

在资源配置效率方面，房价上涨本身也吸引了实体经济企业（如工业等）自身的投资，当这部分企业改变原有投资结构，在资源既定的情况下，把一部分资源投入到房地产行业时，必然挤占了原本应用于设备更新、人员培训和各类开发项目的资金，形成挤出效应。全要素生产率提升的一个重要表现是资源在高生产率行业中所占比重的增加，因而资源从高生产率行业流向低生产率房地产行业必然抑制了全要素生产率增长。基于此，本文提出研究假设3：房价波动会通过减少规模效率抑制全要素生产率增长。

在产出组合方面，中国房地产属于典型的高投高产的粗放型产业，其对国民经济的拉动作用较为明显，但与此同时，房价快速上涨一方面加大了其他行业企业成本，包括土地成本和租金等造成的固定资产成本，以及为了避免劳动力流失而加重的人力资源成本；另一方面也加重了企业职工的购房负担。由于菜单成本和工资粘性的存在，企业的生产成本和职工生活成本难以转嫁，因此，生产成本的上升压缩了企业的利润空间，生活成本的上升则压缩了社会居民消费，最终在利润下降和需求降低的双重冲击下，大部分缺乏核心竞争力的实体经济企业或将面临倒闭，进而恶化了要素产出组合并抑制了全要素生产率增长。基于此，本文提出研究假设4：房价波动会通过剩余混合效率抑制全要素生产率增长。

四、房价波动影响全要素生产率的实证分析

（一）模型变量、样本数据说明及描述性分析

受数据限制，本文使用2007—2016年中国259个地级市作为研究对象。其中，城市发明授权量从中国知网专利数据库检索系统获得；有关金额的数据通过居民消费价格指数或者生产价格指数进行平减处理，并统一单位为万元；其他数据则来源于区域统计年鉴及城市统计年鉴。所有数据均为年度数据。

在模型变量选取方面，本文采用F？覿re-primont指数法来测算城市全要素生产率并进一步分解为技术效率、规模效率和剩余混合效率。在实证中分别以全要素生产率及其三个分解指标为因变量，以房价波动为核心自变量（以商品房销售均价增长率衡量房价波动）。与此同时，城市发明专利授权数能够有力衡量一座城市科技创新能力，客观地反映出地区原始创新能力与科技综合实力，是十分有效的测度城市创新的指标（陈贵富等，2022）。因此，本文借鉴余泳泽和张少辉（2017）的研究，采用各城市每万人占有发明专利授权数来衡量城市创新能力，并加入房价波动与城市创新能力的交叉项。在控制变量方面，由于本文的全要素生产率是以人均GDP、固定资产投资和人力资本分别作为产出指标和投入指标测算而得，为避免模型变量间出现严重多重共线性，本文选取城市创新能力、政府财政自主权、外商投资比例和城市人口变化率作为城市宏观经济环境的控制变量；具体变量的计算情况如表1所示。

（二）理论模型的构建

1.全要素生产率的测算及分解

总产出与总投入的比值可以用来表示多种生产要素投入的全要素生产率，假设q 别为i市第t年的产出向量和投入向量，并令Qit≡Q（qit）和Xit≡X（xit）分别为投入和产出的总函数，则第t期的全要素生产率表达式为：

将式（7）整理得：

TFPit=TFP*×OTEit×OSEit×RMEit  （8）

式（8）为FP指数下全要素生产率完全分解的最终公式。

测算结果如图1所示，各区域的全要素生产率除了在金融危机后的2009年都显著下滑外，其余年份大体都呈现相同上浮趋势。此外，东部地区全要素生产率显著高于全国及其他城市平均水平，中部地区与其他区域之间的差距则逐年拉大。

2.面板数据模型的构建与分析

经过Hausman检验，认为固定效应模型的拟合效果优于随机效应模型。因此，本文采用如下的面板数据固定效应模型：

式（9）—（12）中i代表我国各地级市，t代表各个年份，ε是随机误差项，β0表示截距，？茁i（i=1，2，…6）为各个自变量的估计系数。其中，式（9）是房价波动影响全要素生产率的模型，式（10）—（12）只有被解释变量不同，分别用技术效率、规模效率和剩余混合效率作为被解释变量，起着揭示房价波动如何影响全要素生产率的作用。

3.空间滞后模型

由于邻近的城市发展过程中存在显著的区域经济联动作用，因此城市的经济水平、全要素生产率和房价等因素存在空间溢出效应。为了突破面板数据模型无法揭示各城市房价的空间溢出效应的限制，将进一步通过空间计量模型厘清城市房价波动对全要素生产率的影响机制，阐释区域内各城市房价的空间自相关性及其对全要素生产率的影响。

目前学界认可的三类主流空间计量模型分别是：空间滞后（SLM）模型，设定因变量相互影响；空间误差（SEM）模型，即误差项相互影响；空间通用模型（SAC），是前两个模型的综合形式，即因变量和误差项都相互影响（王庆喜，2014）。

空间滞后模型的基本形式为：

（13）

其中，参数β表示了模型中自变量对因变量的影响程度，Wy为内生变量，是因变量的空间滞后向量，其空间自回归系数ρ反映了相邻区域对本区域的影响。该模型认为一个被测单元的行为会受到自身和邻居的双重影响。若ρ显著，则表明因变量间确实存在明显的空间依赖，ρ的大小则反映了各单元间空间扩散或空间溢出等相互作用的程度。

这里使用式（14）—（17）来识别和测度我国相邻地级市间全要素生产率在空间上的溢出效应。

（17）

其中，式（14）把邻市房价波动和城市人口变化率等作为自变量，探究对本市全要素生产率的影响；W为空间权重矩阵，包含了W·TFPit、W·OTEit、W·OSEit和W·RMEit四个空间滞后变量，分别代表相邻城市全要素生产率、技术效率、规模效率和剩余混合效率，TFPit、HPGit、IAit、HPGIAit、FDit、FDIit、PCRit分别表示第i市的全要素生产率、房价波动、城市创新能力、房价波动与城市创新能力的乘积、财政自主权、外商投资以及城市人口变化率，α1～α6分别反映了各变量对因变量的影响程度。系数ρ的作用是揭示空间滞后变量对本市的影响，系数大小反映了各单元间相互作用的程度占测度单元总体变动的比例，ρ？缀（-1，1）。

4.空间误差模型

为了充分考慮空间依赖的因素，如可能是由遗漏了某些变量导致的，这些遗漏变量可能会对多个单元均具有影响，可以用误差项反映这种影响效应，故模型中应该加入误差项（王庆喜，2014）。设定为：

（18）

其中，λ是误差项的空间自回归系数，Wε是空间误差项的空间滞后向量；μ为扰动项，满足不相关、均值为0、同方差的基本假定。

引入空间误差项的空间面板回归方程为：

（22）

式（19）—（22）参数的含义与式（14）—（17）一致，故不再赘述；其中，λ为误差项的空间自回归系数。

（三）全国视角下房价波动对全要素生产率的影响分析

1.全要素生产率的空间溢出效应检验

这里采用莫兰值方法（MoranⅠ）来分析全国259地级及以上城市全要素生产率（TFPit）、技术效率（OTEit）、规模效率（OSEit）和剩余混合效率（RMEit）的空间溢出效应。表2显示了各地级市各指标在2007—2016年期间的空间自相关走势，各个指标的莫兰值分别处在区间[0.18，0.33]、[0.24，0.30]、[0.021，0.19]和[-0.032，0.13]内。显然，各城市的全要素生产率、技术效率和规模效率的莫兰值基本都通过了1%的显著性检验（除2007年和2013年出现负的莫兰值而不显著外，剩余混合效率的莫兰值仅有2016年不显著）。这表明在全国范围内，城市全要素生产率、技术效率、规模效率和剩余混合效率均呈现出显著的正空间溢出效应，且近几年这种空间溢出效应有逐年扩大的趋势。

2.房价波动对全要素生产率的影响及其影响路径分析

这里以房价波动为自变量，分别以全要素生产率、技术效率、规模效率和剩余混合效率为因变量建立实证模型。首先需要选择合适的空间计量模型，目前学界中，有一些指标可以辅助判断哪种模型形式更贴合实际数据，如LM-lag检验、LM-error检验、两个稳健R-LMlag检验、R-LMerror检验、AIC准则和LOG likelihood等指标。可以从空间相关性检验结果选择合适的模型形式，若LM-lag在统计上比LM-error显著，且R-LMlag显著而R-LMerror不显著，则选用空间滞后模型；反之，若LM-error比LM-lag统计上更显著，而R-LMerror显著而R-LMlag不显著，则选用空间误差模型；若LM-error和LM-lag都不显著，则采用普通面板模型（Anselin，1995）。本文依次进行了普通面板回归分析、极大似然估计法下的SLM回归和SEM回归，并省去了单位根检验和协整检验，这是因为在面板回归中不需要担心出现伪回归问题，并会给出一致估计（Philips and Moon，2000）。由F检验和Hausman检验结果决定选用固定效应模型进行实证，通过对式（9）—（12）进行实证分析得到表３。

表3分别为房价波动对全要素生产率、技术效率、规模效率和剩余混合效率的回归结果。可以看出，房价波动对全要素生产率的估计系数在5%的显著水平上为负，房价每上升1%时，全要素生产率显著降低0.059%，故研究假设1成立。这与陈斌开等（2015）的研究结论相近，该文指出房价每上涨1%，全要素生产率下降0.045%，资源再配置效率下降0.062%。根据回归结果，由于2007年和2016年的全国商品房销售价格分别为3863元和7476元①，这期间房价累计增长了93.5%，由此导致我国全要素生产率将下降5.52%，可见房价波动对全要素生产率具有显著抑制作用。此外，城市创新能力在1%的置信水平上显著促进全要素生产率，而房价波动与城市创新能力的交叉项也在10%的置信水平上与全要素生产率正相关，这表明房价波动通过与创新水平的协同作用促进了全要素生产率，在一定程度上缓解了房价波动对全要素生产率的抑制作用。其次，房价波动对技术效率和剩余混合效率没有明显影响，说明研究假设2和4不成立。但房价波动对规模效率具有显著的抑制作用，由此说明研究假设3成立，也即房价波动是通过影响规模效率进而抑制城市全要素生产率的。规模效率是通过优化资源配置使得全要素生产率增长的重要组成部分，反映了当生产要素等比例增加时，产出增加的比例大于要素投入量增加比例的情况，也即房价波动通过降低规模效率进而抑制全要素生产率提升。这与现实情况也相吻合，房价上升促使有限资金集中于低外部性的房地产业，这种资源错配削弱了生产要素投入的规模效率，抑制了全要素生产率增长。最后，从控制变量来看，政府财政的独立性、外商投资对全要素生产率均具有显著的负面影响，这表明地区的财政支出增加或者财政收入减少均不利于全要素生产率增长。由于全要素生产率提升包括产业升级和优化资源配置两个方面，财政收入的减少意味着政府对高新技术企业的补贴力度减少，政府在优化本地区资源配置效率及效益和升级产业结构方面的扶持作用有所减弱，从而抑制全要素生产率的提高；而外商投资可能并未真正促使企业创新，外商企业对关键技术的非公开在一定程度上决定了其无法促进我国城市全要素生产率的提升。城市人口的变化与全要素生产率呈负相关性，但没有通过显著性检验，这说明城市人口的净流入无助于提升该城市的全要素生产率，因为决定资源配置是否能优化和产业转型是否能升级的要害在于是否引入了高技术人才；与此同时，频率较高的劳动力人口流动，也会加大企业人才流失、培训成本提升和发展的不确定性，抑制全要素生产率增长。

从式（14）—（17）和式（19）—（22）的回归结果来看，空间滞后模型和空间误差模型中各变量的系数符号和显著性基本一致，而固定效应空间滞后模型的回归效果更为显著，故选取此模型进行后续分析。

表4是房价波动对全要素生产率及影响路径的固定效应空间滞后模型回归结果，可以看出，全要素生产率、技术效率、规模效率和剩余混合效率的空间滞后变量系数分别为0.47、0.45、-0.46和0.41，均显著。全国范围内相邻城市全要素生产率、技术效率和剩余混合效率增长对本市对应的经济变量均具有显著的正向空间溢出效应；但相邻城市規模效率则对本市规模效率存在负溢出效应，这说明本市规模效率与邻市的规模效率的上升在一定程度上是相互排斥的。这可能是由于生产要素可以较快地在区域之间流动，资本便会源源不断地流向资源配置效率较高的区域，资源配置的相似值聚合特征更是加重了这一现象（范斐等，2013）。

对全要素生产率来说，在加入其他空间自相关项后，核心自变量—房价波动的回归系数为-0.00045，且在5%水平上显著，这再次说明在考虑空间因素后城市房价波动对其自身全要素生产率依然存在显著抑制作用，因此，研究假设1再次得到验证。此外，同面板回归结果相似，房价波动对技术效率和剩余混合效率没有显著影响，与规模效率显著负相关，表明在考虑空间因素后，研究假设4依然成立。由此可见，邻市房价快速上涨不仅通过作用于规模效率抑制其自身全要素生产率，而且通过规模效率和全要素生产率的空间溢出效应影响本市的全要素生产率。

（四）不同区域视角下房价波动对全要素生产率的影响分析

为了比较东部、中部、西部和东北地区房价波动对其全要素生产率的影响及路径分析，我们在原有模型基础上加入地区虚拟变量进行不同区域视角下的空间面板回归分析。

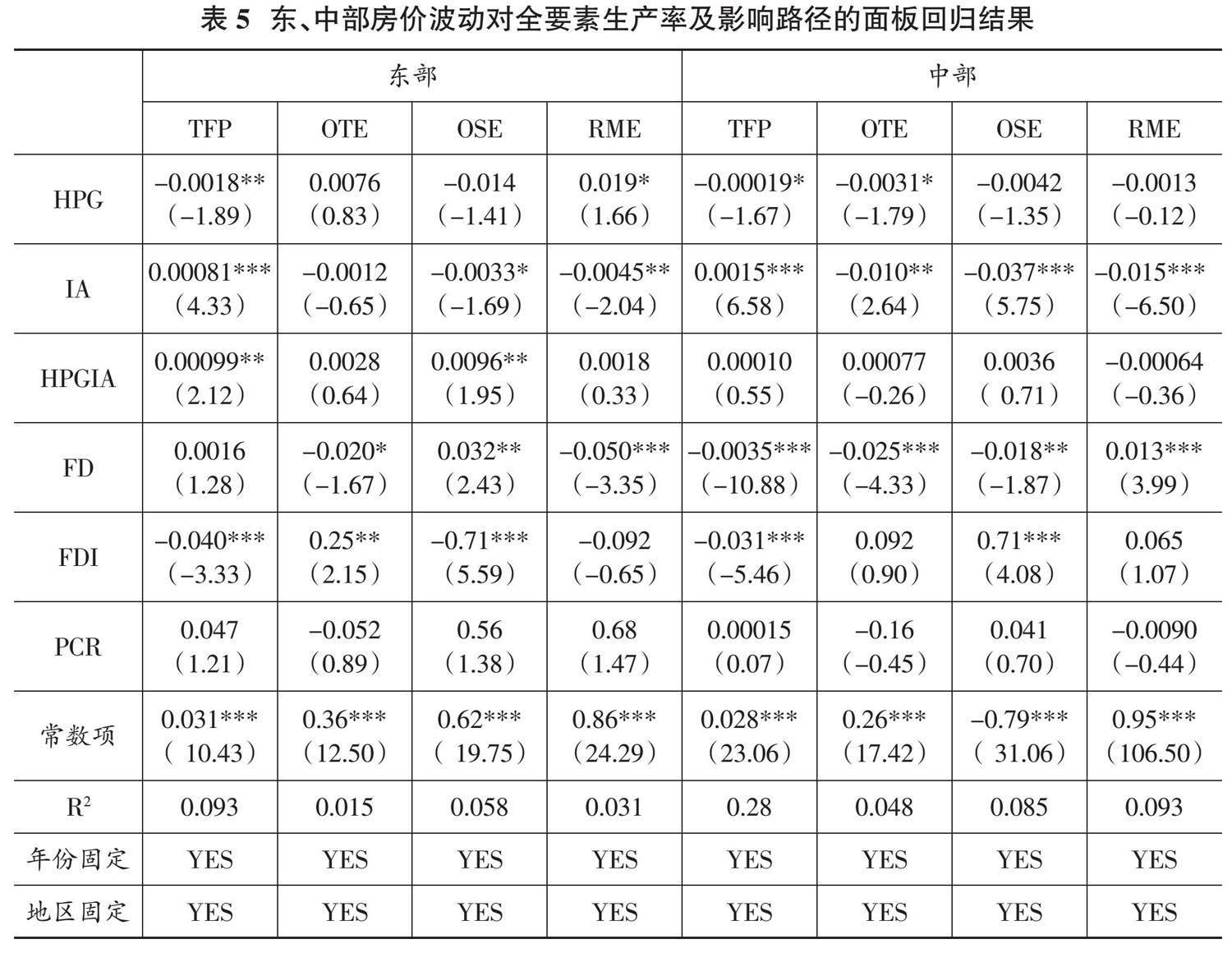
在影响全要素生产率方面，如表5和表6所示，东部、中部、西部和东北地区的房价波动分别在5%、10%、5%和1%的置信水平上抑制了各自地区的全要素生产率。其中，东北地区房价波动对全要素生产率的影响程度最大，其房价每上涨1%，全要素增长率会降低0.91%；东部、中部和西部地区的影响系数则相对较小，分别为-0.0018、-0.00019和-0.0047，说明相比东北地区，这三个区域内房价波动对全要素生产率的抑制程度较小。此外，东部、西部和东北地区的科技创新能力都显著促进了全要素生产率增长；从系数大小上看，东部地区的促进作用最小，而中部地区的科技创新能力对其全要素生产率具有一定的抑制作用；从房价波动与科技创新能力的交叉项来看，仅东部地区的交叉项显著为正，这表明东部地区存在房价波动与科技创新能力的正向协同作用，在一定程度上缓解了房价波动对全要素生产率的抑制作用。从实际情况来看，我国东部地区经济相比其他区域经济更为发达，其科技创新水平和科技创新产业规模明显领先于其他地区而达到平衡阶段，因而该区域的科技创新水平促进全要素生产率提升的边际效应趋于减弱而进入稳定状态。尽管高房价会直接抑制全要素生产率，但由于东部地区中心城市的虹吸效应明显，每年大量的劳动力和技术人才的持续涌入为该区域的经济发展持续注入动力，为企业提供劳动力和产品服务需求，从而在一定程度减缓了高房价对区域全要素生产率的抑制作用。除东部地区外，其他区域的政府财政独立性、外商投资均与全要素生产率呈显著的负相关关系，这说明政府的财政独立性、外商投资均抑制了全要素生产率，这与全国范围的回归结果相同。在人口流动方面，东部、中部的人口流动对全要素生产率呈促进作用，但并不显著；而西部和东北地区的人口流动则抑制了全要素生产率增长，尤其是东北地区近10年来出现的持续人口净外流现象无疑将会进一步降低其全要素生产率水平，并步入恶性循环。

在房价波动对全要素生产率的影响路径方面，同全国范围的影响路径不同，不同区域内房价波动对其全要素生产率的影响路径不尽相同。东部和东北地区房价波动能够显著促进剩余混合效率提升，中部地区房价波动则会显著抑制技术效率提升，而西部地区房价波动则对三种分解效率都没有显著影响。剩余混合效率反映投入及混合比例产出的优化过程（黄祎等，2015）；技术效率则反映相同生产要素投入下，科学进步带来的产出增加，是对现有资源最有效的利用。东部和东北地区房价波动通过减少混合比例产出来间接促进全要素生产率增长。房价波动通过抑制中部地区的技术效率影响其全要素生产率增长，尽管东部地区的技术效率显著高于其他地区，但中部地区在企业管理与科技创新规模这些方面具有一定的后发优势，在中部地区科技水平加速发展的过程中，其易受到更多的经济因素影响且波动更大。高房价改变了企业原来的投资计划，使其目光转移到了房地产行业（Miao and Wang，2014），由于资源既定，使得原本计划用于技术研发的投资减少，该地区高新企业的创新动力和城市的科技进步就受到了抑制，进而阻碍全要素生产率增长。

这里进一步考虑加入空间因素后，采用空间计量模型来分析各区域的情况。由于中部地区房价波动对全要素生产率的促进或抑制作用不明显；西部地区房价波动对三种分解效率的影响也不明显，故回归结果未列出中、西部地区房价波动对全要素生产率影响路径的回归结果。由表7—表9所示，加入空间项后，所有地区全要素生产率均在1%水平上具有显著的正空间溢出效应，其中东部、西部和东北地区房价波动对全要素生产率存在显著抑制作用。

首先，表7表明东部地区房价波动在10%的水平上显著抑制全要素生产率，影响系数为-0.0012，其余变量的变动方向均与不加入空间项时的回归结果相同，在此不再赘述。值得关注的是加入空间项后，房价波动对全要素生产率的影响途径由剩余混合效率变为了规模效率；房价波动抑制了规模效率，影响系数为-0.017，且在5%的置信水平上显著。这表明在东部地区，房价波动通过削弱规模效率来抑制本市全要素生产率，进而影响邻市的全要素生产率。东部地区经济发展水平较高，集中了我国大量的金融、教育和科技资源，资源配置效率对全要素生产率的影响更为敏感。因此当高房价使得资源出现错配时，全要素生产率增长会由于规模效率减弱而被抑制。由此可见，房价波动通过影响资源配置效率给全要素生产率带来的抑制作用比其他路径的影响范围和影响程度都大。

其次，对比表5和表8可以看出，加入空间项后，中部地区的房价波动对全要素生产率没有显著影响，即房价波动仅影响其本市的全要素生产率，并不通过空间溢出效应对邻市产生影响。此外，西部地区房价波动不仅影响本市全要素生产率，也通过空间溢出效应抑制邻市全要素生产率，但这种抑制作用并不以技术效率、规模效率和剩余混合效率为具体影响路径。

最后，表9结果表明东北地区的房价波动显著抑制了全要素生产率。加入空间项后，房价波动通过对规模效率的影响抑制全要素生产率。这一结论与东部城市结果相似，意味着两个区域的经济发展对于资源配置效率更为敏感。其中，东部城市以第三产业为基础，集中了我国大量的经济资源，资源配置的基础较大。而东北地区则以第二产业为基础，虽然资源集中度较低，但东北地区的经济对产业的依赖性较为明显，当资源集中于房地产业导致工业生产要素投入减少时，当地的全要素生产率可能因支柱产业的生产资源分配不足而被削弱。

五、结论与建议

（一）结论

本文利用2006—2017年全国259个地级及以上城市为研究对象，在测算全要素生产率并将其分解为技术效率、规模效率和剩余混合效率的基础上，利用面板固定效应回归和引入空间误差项的空间面板回归模型实证分析了我国各地级市以及东部、中部、西部和东北地区的房价波动对全要素生产率的影响机制。

第一，我国房价波动显著抑制全要素生产率增长，但房价波动与城市创新能力的协同作用在一定程度上减弱了这种抑制作用。高房价城市往往也是经济发达城市且各种资源（人才、技术和资本等）高度聚集，并会对周边区域城市产生“虹吸效应”，进而促进了城市科技创新提升，最终促进了全要素生产率。此外，房价波动会通过降低城市规模效率（而非技术效率和剩余混合效率）进而抑制全要素生产率增长。也即，房价波动对全要素生产率的抑制作用主要表现为对资源配置效率的影响。政府财政的独立性、外商投资对全要素生产率均具有显著的负面影响，这表明地区的财政支出增加或者财政收入减少均不利于全要素生产率增长。

第二，房价波动通过空间溢出效应抑制邻市全要素生产率。在考虑全要素生产率的空间自相关性后，我国城市房价波动依然会通过降低规模效率来抑制全要素生产率的提升；同时，我国城市全要素生产率存在空间上的正溢出，因此本市房价波动不但抑制自身全要素生产率，还会通过空间溢出效应来抑制邻市全要素生产率增长，这凸显出房价波动对全要素生产率抑制效应的空间扩散性。

第三，国内各区域（东部、中部、西部、东北地区）房价波动对全要素生产率的直接抑制程度存在明显差异。其中，东北地区房价波动对其全要素生产率的直接抑制效应最大，而其他三个地区的直接抑制效应相对较小。东部、西部和东北地区的科技创新能力都促进了全要素生产率增长；东部地区的促进作用最小，而中部地区的科技创新能力对其全要素生产率具有一定的抑制作用；东部地区存在房价波动与科技创新能力的正向协同作用，在一定程度上缓解了房价波动对全要素生产率的抑制作用。除东部地区外，其他区域的政府财政独立性、外商投资均无助于提升全要素生产率。东部、中部的人口流动对全要素生产率具有微弱的促进作用，而西部和东北地区的人口流动则抑制了全要素生产率增长；尤其是东北地区多年来出现的持续人口净外流则显著降低其全要素生产率水平。

第四，国内各区域（东部、中部、西部、东北地区）房价波动对全要素生产率的间接影响路径存在明显差异。东部和東北地区的房价波动会通过显著促进剩余混合效率来提升产出组合效率，进而间接促进地区全要素生产率。中部地区房价波动则通过降低技术效率来抑制全要素生产率；在考虑各区域的空间影响因素后，东部和东北地区房价波动通过规模效率来抑制本市和邻市全要素生产率，而其他区域的间接影响路径则不明显。

（二）政策建議

第一，调控城市房价水平处在合理区间，注重短期调控与长效机制相结合，以实现城市房价与其全要素生产率增长的协调发展。由于房价波动显著抑制全要素生产率的增长，要提升城市经济增长质量，就必须重视房地产的平稳运行作用，防止其过快上涨造成地区资源分配的不合理，同时采取措施缓解房价，通过降低城市规模效率的途径来降低全要素生产率。

第二，提升外商投资质量，发挥政府引导作用鼓励资本密集型和技术创新型企业发展。一方面，要改变传统招商引资只注重投资规模而忽视投资产业结构及其经济质量的做法，通过有意识的引入城市产业升级所需的外商投资项目来充分发挥外商投资对城市全要素生产率的积极促进作用；另一方面，政府要通过降低企业和个人的税费来缓解由于高房价所带来的过高企业生产成本和居民生活成本，与此同时，通过引导性政策鼓励我国低收入地区的劳动密集型企业向资本密集型和技术创新型企业转换，最终促进城市全要素生产率提升。

第三，稳步有序提升城市固定资产投资，继续改善投资结构，重视高技术产业投资。科学统筹社会投资与房地产业稳定发展，防止资本过度集中于房地产业，提升金融资源的配置效率，用好社会固定资产投资规模对全要素生产率的正向促进作用，以地方政府专项债带动扩大有效投资，保障社会投资持续稳定增长，为优化城市经济发展质量提供良好的发展背景。

第四，加快多层次智慧城市群建设，促进城市跨域协同发展，使得各类资源在城市群中协同分配，打通多领域跨界壁垒，推进区域一体化建设，实现城市群的全要素生产率提升及高质量发展。目前，我国已经启动城市群建设，初步形成长三角、珠三角、环渤海、中西部四大智慧城市群，但传统一线城市“北、上、广、深”依旧加速聚集着人才、资本及高新技术等生产要素，资源聚集使得房价也持续上涨，不但不利于城市自身的创新发展，还抑制了周边城市的全要素生产率提升。因此，仍旧需要加快多层次智慧城市群建设，推动跨域信息共享及多样资源的优化配置，促进整个区域的科技创新能力和全要素生产率提升。

（责任编辑：孟洁）

参考文献：

[1]Aigner D，Lovell C A K，Schmidt P，et al.Schmidt.Formulation and Estimation of Stochastic Frontier Production Function Models[J].Journal of Econometrics，1977（6）：21-37.

[2]Anselin L，Florax R J G M.New Directions in Spatial Econometrics[M].Berlin：Springer，1995.

[3]Bjurek H.The Malmquist Total Factor Productivity Index[J].Scandinavian Journal of Economics，1996（2）：303-313.

[4]Charnes A，W W Cooper，E Rhodes.Measuring the Efficiency of Decision Making Units[J].European Journal of Operational Research，1978（2）：429-444.

[5]Chen K，Guan J.Measuring the Efficiency of China's Regional Innovation Systems：Application of Network Data Envelopment Analysis（DEA）[J].Regional Studie，2012（3）：355-377.

[6]Denison E，Dward F.The Sources of Economic Growth in the United States and the Alternatives Before US[M].In：A Supplementary Paper of the Committee for Economic Development，New York：Committee for Economic Development，1962.

[7]Hsieh C T，Klenow P J.Misallocation and Manufacturing TFP in China and India[J].Quarterly Journal of Economics，2009，124（4）：1403-1448.

[8]Miao J，Wang P.Sectoral Bubbles，Misallocation，and Endogenous Growth[J].Journal of Mathematical Economics，2014（8）：153-163.

[9]Kumbhakar S C，Denny M，Fuss M.Estimation and decomposition of productivity change when production is not efficient：a paneldata approach[J].Econometric Reviews，2000（4）：312-320.

[10]Odonnell，Christopher J.An aggregate quantity framework for measuring and decomposing productivity change[J].Journal of Productivity Analysis，2012，38（3）：255-272.

[11]Odonnell，Christopher J.An Aggregate Quantity-Price Framework for Measuring and Decomposing Productivity and Profitability Change[J].Centre for Efficiency and Productivity Analysis Working Paper，2008.

[12]Phillips P J，H Moon，Rizvi S A，et al.The FERET evaluation methodology for face-recognition algorithms[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2000（10）：900-1104.

[13]Restuccia Diego，Richard Rogerson.Policy Distortions and Aggregate Productivity with Heterogeneous Plants[J].Review of Economic Dynamics，2008（11）：707-720.

[14]Robert I，Lashitew A A，Timmer M P.The Role of Resource Misallocation in Cross-country Differences in Manufacturing Productivity[J].Macroeconomic Dynamics，2014，21（3）：733-756.

[15]陈斌开，金箫，欧阳涤非.住房价格、资源错配与中国工业企业生产率[J].世界经济，2015（4）：77-98.

[16]陳贵富，韩静，韩恺明.城市数字经济发展、技能偏向型技术进步与劳动力不充分就业[J].中国工业经济，2022（8）：118-136.

[17]陈彦君，郭根龙.数字化转型、产业链整合与全要素生产率[J].海南金融，2024（2）：3-18.

[18]程郁，陈雪.创新驱动的经济增长——高新区全要素生产率增长的分解[J].中国软科学，2013（11）：26-39.

[19]范斐，杜德斌，李恒，等.中国地级以上城市科技资源配置效率的时空格局[J].地理学报，2013，68（10）：1331-1343.

[20]郭萍，余康，黄玉.中国农业全要素生产率地区差异的变动与分解——基于F？覿re-primont生产率指数的研究[J].经济地理，2013（2）：141-145.

[21]郭庆旺，贾俊雪.中国全要素生产率的估算：1979—2004[J].经济研究，2005（6）：51-60.

[22]黄祎，孙广生，黄金枝.全要素生产率分析新方法：F？覿re-primont指数[J].东北大学学报（自然科学版），2015（3）：448-452.

[23]姜永宏，蒋伟杰.中国上市商业银行效率和全要素生产率研究——基Hicks-Moorsteen TFP指数的一个分析框架[J].中国工业经济，2014（9）：109-121.

[24]焦翠红，陈钰芬.R&D资源配置、空间关联与区域全要素生产率提升[J].科学学研究，2018（1）：81-92.

[25]刘秉镰，武鹏，刘玉海.交通基础设施与中国全要素生产率增长——基于省域数据的空间面板计量分析[J].中国工业经济，2010（3）：54-64.

[26]刘宏伟，吴杰，梁雯，等.中国公路运输全要素生产率时空演化及区域竞争——基于Hicks-Moorsteen指数框架[J].地理科学，2017（11）：1640-1648.

[27]刘康.突破“藩篱”：少子老龄化与全要素生产率提升[J].海南金融，2024（2）：19-30.

[28]王庆喜，蒋烨，陈卓咏.区域经济研究实用方法：基于ArcGIS、GeoDa和R的运用[M].北京：经济科学出版社，2014.

[29]王文春，荣昭.房价上涨对工业企业创新的抑制影响研究[J].经济学（季刊），2014（2）：465-490.

[30]魏下海，王岳龙.城市化、创新与全要素生产率增长——基于省际面板数据的经验研究[J].财经科学，2010（3）：69-76.

[31]吴敏洁，程中华，徐常萍.R&D、FDI和出口对制造业环境全要素生产率影响的实证分析[J].统计与决策，2018（14）：132-136.

[32]徐晔，宋晓薇.金融资源错置会带来全要素生产率减损吗？ [J].产业经济研究，2016（2）：51-61.

[33]颜鹏飞，王兵.技术效率、技术进步与生产率增长：基于DEA的实证分析[J].经济研究，2004（12）：55-65.

[34]杨剑波.R&D创新对全要素生产率影响的计量分析[J].经济经纬，2009（6）：19-22.

[35]易纲，樊纲，李岩.关于中国经济增长与全要素生产率的理论思考[J].经济研究，2003（8）：13-20.

[36]余静文，谭静，蔡晓慧.高房价对行业全要素生产率的影响——来自中国工业企业数据库的微观证据[J].经济评论，2017（6）：22-37.

[37]余泳泽，张少辉.城市房价、限购政策与技术创新[J].中国工业经济，2017（6）：98-116.

[38]余泳泽，张先轸.要素禀赋、适宜性创新模式选择与全要素生产率提升[J].管理世界，2015（9）：13-31.

[39]朱晨.上海市房价增长对工业企业创新的影响——基于劳动力成本视角的再审视[J].经济经纬，2018（3）：96-102.

[40]朱喜，史清华，盖庆恩.要素配置扭曲与农业全要素生产率[J].经济研究，2011（5）：86-98.