顾及多因子的江苏省大气加权平均温度精化模型

毛吉伟

关键词： 加权平均温度 探空站数据 单因子模型 多因子模型 精度评估

中图分类号： P228.4;P412 文献标识码： A 文章编号： 1672-3791（2024）01-0162-04

水汽是大气活动中最活跃的一种气象成分，在大气演变中扮演著重要的角色。随着地基GPS （Global Positioning System）气象学的不断发展，运用地基GPS来反演大气可降水量成为了大气水汽探测的一种新手段。它的时空分辨率和精度较高，造价便宜，且操作简单，实时连续，不受天气状况的影响，可以全天候大范围地作业，是探测大气水汽传统方法的有力补充［1-3］。因此，大量的国内外学者围绕地基GPS 气象学开展了一系列的研究工作。地面GPS 接收机接收到的卫星信号需要通过对流层区域，在对流层区域，GPS 信号由于对流层折射的影响进而产生对流层延迟，而对流层延迟可以通过某种转换将对流层湿延迟转变成大气可降水量（Precipitable Water Vapor，PWV）。一般对流层模型中，对流层天顶总延迟（Zenith Total Delay，ZTD）包含对流层静力学延迟（Zenith Hydrostatic Delay，ZHD）和对流层湿延迟（Zenith Wet Delay，ZWD）这两部分。其中，ZTD 和ZHD 可在GPS 定位时精确获得，两者作差可得到ZWD。将ZWD 转换成PWV 需获取转换系数Π，它们的转换关系为PWV =Π× ZWD，而加权平均温度T_m就是获取转换系数Π的重要参数，大气加权平均温度T_m的精度直接影响着PWV 反演的精度，因此如何提高T_m的精度就显得尤为重要［4-22］。

目前，国内外已有许多学者针对不同地区的大气加权平均温度及相关参数进行了研究，建立了不同的T_m模型。例如：Bevis 等人［12］根据美国中纬度区域的探空资料建立的T_m～T_s线性回归模型，即Bevis 模型；龚绍琦［10］按照全国不同气候和不同季节分区的方法，对探空数据进行线性回归，建立了T_m的单因子和多因子模型，该模型利用的方法是最小二乘原理，广泛适用于中国地基GPS 水汽反演过程中T_m的计算；何士伟等人［1］通过分别研究分析安徽省和香港地区T_m与其他气象因子之间的线性相关性，建立了基于不同变量的单因子模型和多因子模型，并分别与Bevis 模型和李建国模型进行精度比较，验证了其可靠性；谢劭峰等人［6］用线性回归分析了广西地区T_m的时空变化特征，以及T_m与地面温度之间的关系，建立了适用于广西的T_m单因子模型；李国翠等人［9］基于T_m与地面各变量之间的关系，利用最小二乘法建立了华北地区的单变量经验模型和多变量经验模型；王晓英等人［3］将全国分为5个气候区，建立了中国不同气候区的T_m回归模型，并验证了模型的精度。这些模型都充分考虑了T_m值受各种要素影响的变化，同时也证明了区域多变量经验模型的预报精度高于全球经验模型和单变量经验模型。因此，需要根据本地区的实际情况构建适合本地区的加权平均温度模型很重要。

江苏省地处我国东部沿海、长江中下游地区，常年频繁降雨，高精度的预报可降雨量可以有效地进行气象预报、洪涝灾害预警等工作，对于江苏省的天气变化、降水量预测等具有重要意义。本文基于江苏省3个探空站2000—2017 年的实测数据进行建模以及2018—2019 年的实测数据进行模型精度评估。

1 实验数据与计算方法

1.1 实验数据

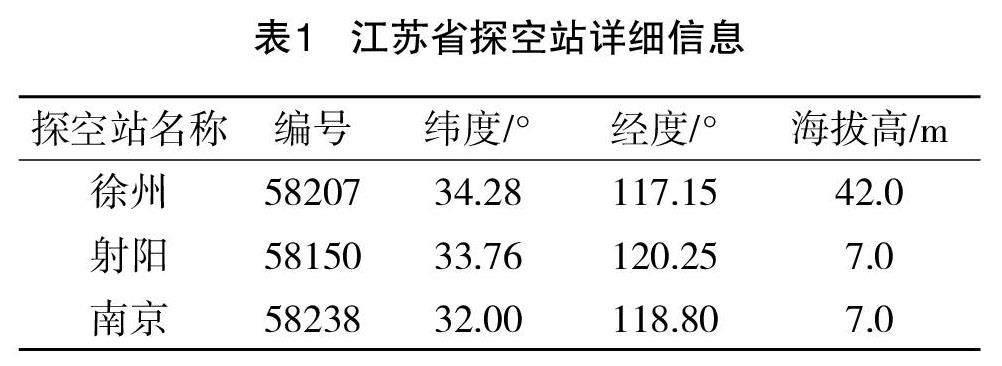
本文利用江苏省徐州、射阳、南京这3 个探空站2000 年1 月1 日至2019 年12 月31 日的数据进行分析建模和精度评估，其中包括2000—2017 年的拟合数据、2018—2019 年的预测数据（探空站每日收集两次数据，分别在0 点和12 点，采样间隔为12 个小时）。江苏省探空站详细信息如表1 所示。

1.2 大气加权平均温度的计算方法

常见的T_m的计算方法主要有：固定值法、Bevis 模型以及数值积分法。在GPS 气象学中，数值积分法是当前公认精度最高的加权平均温度解算方法［11］。利用数值积分法可以计算得出T_m值，并根据其与T_s之间的线性关系建立回归方程，这也是获得区域加权平均温度模型的重要方法。

天顶湿延迟（ZWD）可以由天顶总延迟（ZTD）和天顶静力学延迟（ZHD）二者作差得出。将ZWD 转换为PWV 的基本公式为

PWV =Π×ZWD （1）

在式（1）中：Π为水汽转换系数，是与T_m有关的函数，表达式为

3.2 江苏省加权平均温度模型评估

为了验证本文提出的模型有效性，利用江苏省探空站2018—2019 年实测数据对模型精度进行全面评估，结果如表3 所示。

经过表3 对比发现，江苏省3 种本地化模型的预报精度均优于Bevis 模型。这3 种本地化模型中，2018—2019 年多因子模型T_m3RMSE 为3.01 K，比多因子模型T_m2 提高0.23 K，比单因子模型T_m1提高0.38 K。因此，T_m3经验模型的预报效果均优于其他两种本地化经验加权平均温度模型。此外，与Bevis 模型相比，本地化经验加权平均温度模型并无明显的系统偏差，且Tm3 经验模型稳定性最佳。

4 结语

本文利用江苏省3 个探空站18 年的探空数据，依据T_m与各变量之间较强的相关性，拟合出江苏地区的单因子回归模型T_m1和多因子回归模型T_m2、T_m3。其中两个多因子模型均考虑三个气象因素的综合加权平均温度模型，且均考虑地面温度和地面气压；不同的是，T_m2经验模型的另一个变量是水汽压，而T_m3经验模型的另一个变量是水汽压的自然对数。经分析得到如下结论。

（1）单因子模型T_m1 的预报精度高于Bevis 模型，2018—2019 年预测RMSE 为3.39K，较Bevis 模型提高了6.4%。

（2）对比两种多因子加权平均温度模型发现，T_m与T_s、P、ln e 构建的T_m3经验模型精度最高，2018—2019 年预测RMSE为3.01K，较Bevis模型提高了16.8%。

（3）与Bevis 模型相比，本文建立的3 种江苏省本地化模型计算出的T_m值更接近探空站T_m值，计算精度得到了提高。这说明建立适宜的本地化大气加权平均温度模型可以在一定程度上提高T_m的精度，为当地的GPS 反演大气可降水量提供依据。