联合均值和散度逆高斯回归模型的参数估计

张露露，黄希芬

（云南师范大学 数学学院，昆明 650500）

0 引言

众所周知，生产实践中产生的数据在大多数情况下是正偏态数据。因此，对正偏态数据的分析一直是研究者们感兴趣的课题，而这也符合现实需求。统计学中的许多参数模型都适用于正偏态数据的分析。例如，Gamma 分布族由于在数学上可得到显式表达式而备受研究者们的喜爱；逆高斯分布族具有良好的概率和统计性质。邓平稳和谢治州（2022）[1]基于以上两个回归模型，通过对一组房价数据的分析来预测未来的房价走势，结果表明两种模型在预测不同问题时各有千秋。事实上，逆高斯分布因其复杂的表达式及计算过程而远不如Gamma 分布受欢迎。然而，人们发现对于可靠性分析、精算学、生态学等领域中的一些数据，逆高斯分布族更符合其数据特点。

逆高斯分布起源于Brownian 运动问题。随着人们对其了解渐渐深入，也衍生出不同的表达式[2]。人们可根据数据特点、参数估计算法不同等因素而对其进行不同的选择和应用。例如，Chankham 等（2022）[3]基于逆高斯分布变异系数的置信区间对泰国PM2.5的扩散进行分析和研究；Amin等（2021）[4]基于响应变量服从逆高斯分布的假设，构造记忆型控制图，将其应用于纱线制造业；黄顺林等（2010）[5]基于零调整逆高斯回归模型，对一组汽车责任险缺失数据进行了研究；庄会富等（2018）[6]提出将逆高斯分布和KI准则相结合，对影像进行非监督变化检测。除此之外，还有一群学者致力于发展各种算法来求解逆高斯回归模型回归参数的估计值。在均值的假设下，先后发展了岭估计[7]、Liu估计[8]、KL估计[9]等方法；在均值的假设下，除了以上三种估计方法，还有迭代加权最小二乘估计法[1]；在均值μ=的假设下，发展了贝叶斯估计法[10]。显然，在均值参数μ＞0 的必要条件下，第一种和第三种假设有明显的局限性，即必须大于0。另一种回归模型是联合均值和散度模型，即假设均值参数和散度参数分别对应各自的回归参数。具体地，假设均值参数，散度参数。在估计参数时，涉及Fisher信息矩阵[11,12]以及EM算法[13]。而对于以上两种逆高斯回归模型，除了贝叶斯估计法，上述其他方法都涉及矩阵求逆的问题，即算法的有效性依赖于矩阵是否奇异。

基于以上方法的局限性，本文立足于联合均值和散度逆高斯回归模型，将Minorization-Maximization（MM）算法[14]用于求解两类回归参数的极大似然估计。MM算法本质上是EM算法的一种延伸，但其在处理多元函数方面又具有EM算法不具备的优势，比如可以绕开多元函数求积分问题，通过合适的不等式把多元目标函数转化为一系列低维函数之和，甚至可能把感兴趣的未知参数彼此分离开，而在这之后求解函数最值问题时可绕开矩阵求逆的局限性。MM 算法由于其应用的灵活性以及计算简便等优点，已被广泛应用于各种问题的研究，比如变量选择[15]、分位数回归[16]、半参数模型等。

1 MM算法原理简介

假设已知l(θ|Yobs)为目标函数，其中，Yobs为数据观测值，向量θ=(θ1，θ2，…，θq)′∈Θ，Θ是参数空间，θ是感兴趣的未知参数。则参数向量θ的极大似然估计为θ^=。在极大化目标函数l(θ|Yobs)时，往往会涉及复杂的计算过程，其一阶导函数在通常情况下也没有解析解，这时常常要用到数值方法，如采用Newton-Raphson 迭代算法求其近似解，而这在多元函数情况下又涉及矩阵是否可逆的问题。因此，MM算法提供了另一种求解思路。MM算法主要分为两个步骤：第一步是Minorization步骤，该步骤是至关重要的一环，其关键是寻找到合适的不等式，通过不等式放缩构造目标函数l(θ|Yobs)的一个极小化函数（或称作替代函数）Q(θ|θ(k))，使其满足：

其中，θ(k)是θ的第k次迭代值。若此时的替代函数还不尽如人意，则可把该替代函数看作新的目标优化函数，继续重复第一个步骤的思想。第二步是Maximization步骤，顾名思义即极大化替代函数，从而得到参数向量θ的极大似然估计值。

2 联合均值和散度逆高斯回归模型

2.1 模型介绍

假设响应变量Yi～Inverse Gaussian(μi，τi),且相互独立，i=1，2，…，n，则其概率密度函数为：

其中，均值参数μi＞0 且满足lnμi=X′i β，散度参数τi＞0 且满足lnτi=,Xi=(xi1，xi2，…，xiP)′和Zi=(zi1，zi2，…，xiJ)′是解释变量，β=(β1，β2，…，βP)′是均值模型的未知参数，η=(η1，η2，…，ηJ)′是散度模型的未知参数,β和η是待估计的回归参数。

对应的对数似然函数为：

其中，c是与待估参数无关的项，可视作常数。l1(η|Yobs)，l2(β，η|Yobs)和l3(β，η|Yobs)分别为：

2.2 应用MM算法进行参数求解的步骤

本文的目的是把MM 算法应用到联合均值和散度逆高斯回归模型，求解两类回归参数的极大似然估计值。在开发MM 算法时，最大的困难在于第一步，即构造一个合适的极小化函数，而成败的关键在于找到合适的不等式，这需要具体问题具体分析。在实际问题中，尤其是涉及高维模型时，MM 算法更吸引人的地方在于，可将替代函数构造为参数分离的低维函数之和，把高维优化问题转化为低维优化问题，从而降低计算的复杂度。

本文希望找到对数似然函数l(β，η|Yobs)的一个替代函数，将参数向量β和η分离开，进而可以分别对其进行观察和研究，然后再把各个分量从其向量中分离出来，即最终的替代函数形式是一系列一元函数之和，从而绕开了求解过程中的矩阵奇异性问题。

观察式（2）可知，可把目标函数l(β，η|Yobs)重写为三个函数（式（3）至式（5））的和。接下来，根据各个函数的特点逐一分离β和η，分别为其找到合适的替代函数。通过观察可知，l1(η|Yobs)已与β无关，而l2(β，η|Yobs)和l3(β，η|Yobs)则需要借助MM算法分离β和η。对于，可利用算术-几何均值不等式[17]将待估参数η和β分离，即利用不等式：

其中，c是与待估参数无关的项。

基于式（6）和式（7），可将函数l2(β，η|Yobs)和l3(β，η|Yobs)中的β和η分离开，从而得到只关于未知参数η的替代函数：

以及只关于未知参数β的替代函数：

观察Q1(η|Yobs)和Q2(β|Yobs)可知，分别直接对其进行极大化是得不到解析解的，因此本文借助Newton-Raphson算法进行迭代求解。但在实际应用时，并不能保证矩阵总是非奇异的，为了避免遇到此类问题，接下来将继续借用MM算法分别对参数向量η和β进行分量分离，将多元函数Q1(η|Yobs)和Q2(β|Yobs)分解为多个一元函数之和，从而避开求解极大似然估计时矩阵求逆时遇到奇异矩阵的问题。

当ωij=0 时，令。根据离散型Jensen 不等式[14]，构造如下不等式：

从而可将η1，η2，…，ηJ从函数Q1(η|Yobs)中分离开来，得到J个新的替代函数，即：

其中，Q1j(ηj|Yobs)是只关于参数ηj的一元函数。令∂Q1j(ηj|Yobs)∂ηj=0，利用Newton-Raphson 算法进行迭代求解，可得ηj的迭代公式为：

综上所述，可得到如下迭代算法：

3 数值模拟

本文通过模拟研究来说明MM 算法在求解联合均值与散度逆高斯回归模型的参数极大似然估计值时的可行性和有效性。

模拟研究的随机数据由以下模型产生：

为了避免两类回归参数因分量个数不同、真值取值不同而可能引起的模拟效果不同，设定P=J=5,两类回归参数向量取相同的值，即β=η=(-2，-1，0.5，1，2)′。接下来，通过设计不同的解释变量值来分析两类解释变量的取值是否会影响均值模型对应的回归参数和散度模型对应的回归参数的估计结果。具体实验设计如下：

实验一：两类解释变量之间相互独立，且组内也相互独立，且Xip～U(0，1)，Zij～U(0，1)。

实验二：两类解释变量共线，但组内相互独立，即Xip=Zij，Xip～U(0，1)。

除此之外，为研究样本量对两组实验结果的影响，两组实验的样本量n均取{50，100，200，300}。整个模拟由R软件实现，每种情况模拟500次。

表1 中的和是在实验一的条件下，基于500 次模拟样本进行MM算法求解得到的回归参数估计值，取其样本均值，进而求出样本均值与真值之间的偏差（Bias），以及估计值的样本标准差（SD）。随着样本量的增加，两类参数的估计值总体上是越来越接近真值的。具体地，对比各个均值回归参数的偏差绝对值，(β1，β5)=(-2，2)的偏差绝对值随着样本量的增加而一致地减小；(β2，β3)=(-1，0.5)的偏差绝对值总体上越来越小，但β2在样本量n=100、β3在n=300 时的偏差绝对值有所增加，但与其他四组在数值上并没有很大的差异；相比其他四个变量，β4=1 的估计值与样本量之间并没有以上关系，虽然其最大的偏差绝对值不超过0.05，但相比其他变量，这个结果是不理想的。接下来，对比各个散度回归参数的偏差绝对值，前三个回归参数的偏差绝对值随着样本量的增加而一致地减小；η4=1在n=100 时，其偏差绝对值增加，其偏差最大值不超过0.01；除了(n，η5)=(200，2)这组结果波动较大外，η5的偏差绝对值总体上是越来越小的。在样本量相同的条件下，对比两组参数的偏差绝对值，绝大多数情况下都是均值回归参数比散度回归参数的估计效果更好。最后，对比样本标准差可以看出，两组参数都是随着样本量的增加而一致地减小，但依然是前者有着更小的数值。

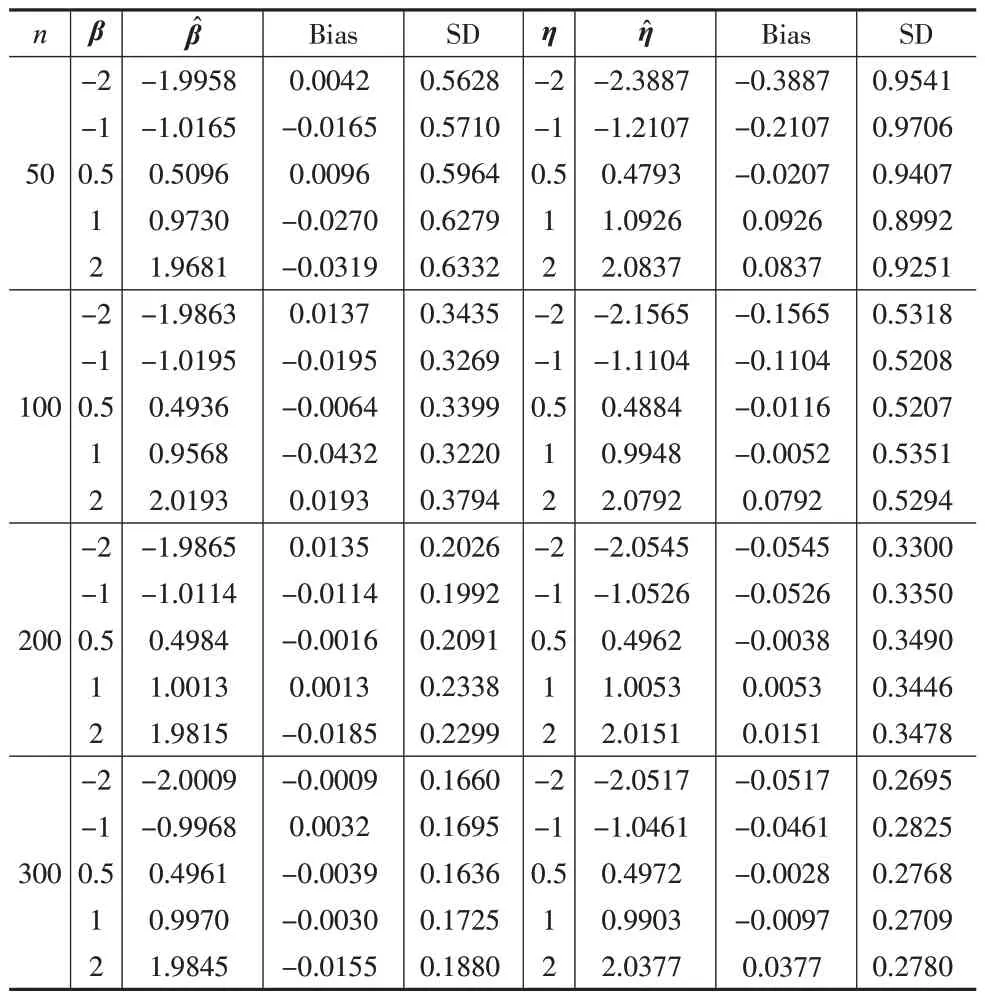
表1 实验一中两组参数向量的每个参数分量的模拟结果

表2是在实验二的条件下对500次模拟样本进行MM算法求解得到的数值结果。随着样本量的增加，两类参数的估计值总体上是越来越接近真值的。首先，β1、β2、β3在n=300 以及β5在n=200 时对应的偏差绝对值有所增加，但总体趋势还是样本量的增加有益于模拟效果的优化；β4=1 的估计值与样本量之间并没有以上的趋势，其最大的偏差绝对值不超过0.04。前三个散度回归参数的偏差绝对值随着样本量的增加而一致地减小；η4=1 在n=200 时偏差绝对值增加，在n=300 时显著减小；η5的偏差绝对值随着样本量的增加而减小，但在n=300 时有所增加。然后，对比两组参数的偏差绝对值，从n=100 开始，随着样本量的增加，均值回归参数比散度回归参数的估计效果一致地更好。最后，对比样本标准差可以看出，两组参数随着样本量的增加而一致地减小，但前者模拟效果更好。

表2 实验二中两组参数向量的每个参数分量的模拟结果

表1 和表2 展示了对每个分量进行对比研究的结果，而表3 则通过均方误差（MSE）来研究每组回归参数的整体模拟效果。结果表明：首先，随着样本量的增加，每组实验的模拟效果都越来越好，但显然均值回归参数比散度回归参数具有更好的效果；其次，实验一的结果整体上比实验二的效果好，即数据之间独立比共线具有更好的结果，这也符合以往的理论和实践；最后，不管数据之间的相关性如何，当样本量从50 增加到100 时，整体模拟效果都显著变好，因此在实际应用中，当数据量达到100 时就可以得到一个很接近实际情况的结果。

表3 两组参数向量分别在两组实验中的MSE

综上所述：首先，均值回归参数的模拟效果总体上比散度回归参数的模拟效果更好；其次，两组解释变量之间是否共线对结果的影响并不显著；最后，样本量的增加可以改善模型的结果，且在实际应用时，当数据量达到100时就可以得到一个很好的估计结果。

4 实例分析

本文用一组实际数据检验该方法的实用性。该数据集[12,18]共收集了125 组数据，涉及5个变量（见表4）。具体地，先记录下汽油罐的初始罐温以及初始气压，当该油罐装满汽油后，再记录下其温度和气压，以及设备回收的碳氢化合物重量。将以上实验重复125 次，则可收集到125组数据。

表4 变量说明

把设备回收的碳氢化合物重量设为响应变量Y,且Yi～Inverse Gaussian(μi，τi)，i=1，2，…，125，再将剩下4个变量设为解释变量，具体的变量说明见表4。已有研究[12,18]通常只取其中的32组数据进行建模求解，但本文的数值模拟结果表明，当数据集达到100组时得到的结果更接近实际情况，所以对全部125组数据进行建模求解。本文的目的是研究一组解释变量对逆高斯分布的均值参数和散度参数是否有影响，以及哪些变量有显著影响，故模型假设X=Z。

为了检验参数估计值的显著性，本文采用Bootstrap法[19]对数据集进行抽样，得到一组Bootstrap 样本集，再用MM算法估计该组样本集下的回归参数，重复该过程B次得到B组参数结果。记。若每个参数的B个估计值具有正态性，则可构造如下的t分布置信区间：

若每个参数的B个估计值不具有正态性，则可构造如下的百分位置信区间：

本文基于逆高斯联合均值和散度回归模型，先运用MM算法求解得到参数的极大似然估计值（MLE），再利用上述Bootstrap 方法得到B=20000 组参数估计值，最后基于显著性水平α=0.05 分别计算得到t分布置信区间以及百分位置信区间，具体结果见表5。对比估计值，发现两组回归参数有着不同的估计值，其中解释变量(X3，X4)有着相反的符号。观察t分布置信区间，发现汽油温度X2、初始气压X3及汽油气压X4都对逆高斯分布的均值有显著影响；初始罐温X1和汽油气压X4对散度有显著影响，该结论与已有的研究结果[19]一致。再观察百分位置信区间，发现汽油温度X2以及汽油气压X4都对逆高斯分布的均值有显著影响；初始罐温X1、初始气压X3以及汽油气压X4对散度有显著影响。

表5 参数估计值及其两种Bootstrap置信区间

5 结束语

响应变量服从逆高斯模型的数据在实践中普遍存在，许多学者也致力于这方面的研究。基于不同的现实背景，人们会着眼于不同的均值回归参数形式，也有研究散度回归模型的，但同时对均值和散度参数进行回归分析的研究相对较少。本文对联合均值和散度逆高斯回归模型进行了探讨，在求解模型参数的极大似然估计时，由于逆高斯概率密度函数的表达式复杂，没有显式解，故需借助Newton-Raphson 算法等数值方法，这时求解多元函数值时总是涉及矩阵求逆问题，而要求现实数据总是满足矩阵可逆是不现实的。本文基于MM 算法可以进行参数分离的优良性质，绕开了矩阵奇异问题，为求解回归参数估计值提供了一种新的可能。本文的MM 算法也可以解决只考虑均值或散度具有回归参数形式的逆高斯回归模型。数值模拟及实验分析验证了所提方法的可行性。