基于投资混频数据的中国经济波动预测

岳金秀，陈 尧

（湖北民族大学数学与统计学院，湖北 恩施 445000）

0 引言

一直以来，经济波动预测对国家制定经济政策和企业、部门采取相应措施至关重要。而经济波动与各宏观经济指标密不可分，其中，固定资产投资与经济增长之间具有显著的双向影响关系[1]。在现代经济周期理论中，投资被认为是导致经济波动的主要原因。消费需求基本保持比较平滑的变化，随着国际竞争日渐激烈，以及在扩大内需的大背景下，净出口对经济的驱动作用也在逐渐降低。因此，投资需求是对经济波动影响较大的成分。投资的变动将直接或间接影响经济波动：一方面，投资可以作为资本，直接使GDP增加；另一方面，投资还具有乘数效应，投资的获利会刺激更多的投资，加速消费的刺激作用，促进居民消费。

目前仅根据投资预测经济波动的研究较少，只有少量文献涉及相关内容。如戴卓尔等（2023）[2]引入外商直接投资（FDI），基于“三驾马车”对中国GDP 增长率进行预测，发现引入FDI后不仅预测精度更高，而且实时预测也比未引入FDI的预测更精准。潘雅茹和罗良文（2020）[3]实证检验了固定资产投资对经济高质量发展的推动作用。现有文献已经证实了投资与经济波动之间有显著的相关性。基于此，本文从投资角度构建中国的宏观经济波动预测指标并进行实证分析。随着网络技术的迅速发展，使用网络数据进行预测模型修正成为研究热点。陈卫华和徐国祥（2018）[4]利用股票论坛发帖数增长率预测股票指数波动，发现股票论坛数据对预测精度的提高有所贡献。徐映梅和高一铭（2017）[5]根据百度取词构建了高频和低频舆情指数，提高了对CPI 的预测精度。Hochreiter 和Schmidhuber（1997）[6]从经济学角度给出了个体关注的定义，他认为投资者对资源的认知能力是有限的，个体在单位时间内只能进行有限的信息关注和处理。通常投资者更容易关注表现突出和自己感兴趣的信息。投资者在单位时间内的有限关注行为，体现了对当前项目的关注。当投资者通过网络搜索行为产生了正向、积极的心理预期时，就会转化为投资决策。在整个过程中，网络搜索数据起到了建议和修正的作用。随着深度学习技术的发展，长短期记忆（Long-Short Time Memory，LSTM）神经网络模型因可以更好地学习时间序列之间的长期依赖关系，开始被广泛应用于预测模型中。徐映梅和陈尧（2021）[7]将传统的ARIMA模型与LSTM 模型在我国经济波动预测上比较，发现LSTM 模型在预测复杂的非线性时间序列数据时，能够取得更好的效果。梁龙跃和陈玉霞（2023）[8]结合LSTM模型和小波分析对季度GDP进行预测，结果显示，加入小波分析的LSTM 预测模型具有较好的泛化能力，预测精度更高。然而传统的LSTM神经网络模型在处理混频数据时，模型的学习性能也会受到影响。对此，Neil 等（2016）[9]提出了一种改进的长短期记忆（Phased-LSTM）网络模型，适用于处理异步混频数据的建模。

综上所述，宏观经济波动预测多采用传统计量模型，使用混频数据并利用神经网络模型进行经济波动预测的研究还比较少。本文旨在更好地利用高频数据的原始信息，同时实现变量之间非线性关系的探讨，构建多源混频LSTM模型（Multi Source Mixing LSTM,MM-LSTM），采用政府统计月度数据、网络搜索日度数据以及GDP 季度数据多指标联合，从投资视角研究和预测宏观经济波动。为了验证本文提出的混频数据预测宏观经济波动的有效性，以及构建的MM-LSTM 模型的预测效果，将其与传统的AR模型、MIDAS模型进行对比研究，以评估不同数据以及不同方法的研究结果。

1 研究设计

1.1 统计数据收集与处理

本文基于《中国统计年鉴》中公布的相关数据，同时参考与投资相关的文献，并且兼顾数据的可得性，初步挑选出10个候选指标。包括工业增加值累计增长率[10]、发电量累计增长率[11]、房地产投资累计增长率[12]、制造业采购经理指数（PMI 指数）[13]、固定资产投资额累计增长率[14]等。收集并整理得到上述10 个指标2011 年1 月至2022 年12 月的月度统计数据，并收集整理2011—2022 年国内生产总值指数累计值（上年同期=100）季度数据。对于政府统计数据，进行如下处理：

（1）GDP增长率的构建。本文选用反映一定时期内国内生产总值变动趋势的国内生产总值指数累计值（上年同期=100）作为预测变量。为了消除各指标间的数量差异，把国内生产总值指数累计值（上年同期=100）数据转换为增长率，即GDP 增长率=国内生产总值指数累计值（上年同期=100）-100，记为GDP_IG。

（2）缺失数据处理。根据官方公布的数据，工业增加值累计增长率、固定资产投资额累计增长率、水泥产量累计增长率等指标缺少各年份1月的数据，为了数据的连续性，取2月和3月的均值补全1月的数据。

（3）投资统计指标筛选。计算各指标数据与GDP_IG的皮尔逊相关系数，筛选出与经济波动相关性较高的8个指标，结果如表1所示。

（4）投资统计指数的构建。前文统计指标筛选已经确定了各指标与因变量的强相关关系。但皮尔逊相关系数只能衡量两个变量间的线性关系，而随机森林算法可以有效处理非线性数据，因此采用随机森林算法计算各指标的权重。利用Python中Sklearn机器学习库建立随机森林回归模型，得到各特征的重要性得分。模型输出特征的重要性得分如表2 所示。把每个特征的重要性得分作为每个特征的权重系数，合成一个月度时间序列，记为投资统计指数（Investment Statistics Index，ISI）。

表2 各特征重要性得分

1.2 网络搜索数据指标收集及处理

本文选用百度指数[15]作为网络搜索指数的代表。百度指数的计算是以网民的搜索量为基础，以关键词为统计对象。关键词的选取是合成投资网络搜索指数的重要内容。本文选取“投资”作为关键词，利用文本检索和筛选，在中国知网检索CSSCI期刊，得到5389条记录。下载这些文献，然后利用中文分词技术对标题进行分词，筛选出“投资”“创新”“经济”等100个关键词作为候选关键词。同时利用百度指数需求图谱相关词推荐功能，搜集并整理得到2011 年1 月1 日至2022 年12 月31 日与“投资”“房产”“固定资产”等相关的28 个关键词，将其加入候选关键词中。另外，根据经验取词，选取“发电量”“金融”“GDP”等8 个关键词加入候选关键词中。选取的关键词还需被百度指数收录，因此剔除没有被收录的词，最终整理得到108 个关键词的实时搜索量数据集。对于投资网络搜索数据，数据处理过程如下：

（1）数据预处理。百度指数数据是以日为频率的时间序列，但每月天数并不相等，将日度数据换算成月度、季度等时间序列会产生误差和波动。因此，本文参照徐映梅和高一铭（2017）[5]的方法，将各月份转化为相同的天数。即删除2月29日及5月、7月、8月、10月、12月中每月31日的数据，把1月最后一天的数据作为2月第一天的数据，把3月1日的数据作为2月最后一天的数据。处理后，每年和每月的天数相等。即每月30天，每年均为360天。

（2）消除网络发展趋势。网络搜索数据不但会受到网民关注的影响，而且会受到互联网发展的影响，例如2013年智能手机的逐渐普及，致使手机客户端搜索数量增加。因此，在数据分析之前还需消除网络发展对搜索量波动的影响。借鉴徐映梅和高一铭（2017）[5]的方法，采用与投资关键词相关性较低的中性词来消除网络社会发展对搜索量的影响。

其中，anum为关键词搜索量数据，bnum为中性词“百度”的搜索量数据，Anew为处理后的搜索量数据，记为搜索热度数据。为了防止取对数时出现异常，对所有搜索量值进行加1的平移处理。

（3）筛选核心关键词。获得各关键词的搜索热度数据后，利用时差相关分析，求出关键词搜索热度序列和房地产投资累计增长率的时差和相关系数，进一步筛选重要的关键词①根据各关键词搜索热度序列与选取的8个政府统计指标选择最优时差相关分析结果确定。。利用Python软件编程计算，最终选取23个相关性大于0.5的关键词，其中，相同时差的关键词有18个，具有领先和滞后阶数的关键词有5个，将他们调整为相同时差。这23个关键词将用于投资网络搜索指数的合成。选取关键词的时差阶数和最大相关系数如表3所示。

表3 投资网络搜索指数关键词

（4）投资网络搜索指数的构建。由于选取的关键词数量较多且部分关键词序列存在较强的相关性，因此本文利用因子分析法，使用少数的几个变量来解释众多变量，达到降维的目的，同时又保持较高的解释力。在对关键词序列进行因子分析之前，需要进行KMO 值和Bartlett 球形度检验，检验结果中KMO值为0.96＞0.6，Bartlett球形度检验的P值小于0.05，两个检验均通过。利用SPSS分析软件进行因子分析，前两个因子的累计方差贡献率为85.15%。其中，因子1在商务部、长期投资、发改委、服务业、管理者等12 个成分上有较大载荷，这些关键词主要体现了投资者对实体投资的关注。因子2 在理财、投资公司、风险投资、融资等11个成分上有较大载荷，这些关键词大部分反映了投资者对金融投资的关注。

（5）合成投资网络搜索指数。首先将各因子的成分得分系数作为关键词的权重系数，合成两个因子的月度数据。然后以两个因子的月度数据为特征，以房地产投资累计增长率月度数据为目标变量，利用Python建立随机森林回归模型，得到两个因子的特征重要性。模型输出特征的重要性如表4 所示。最后把每个特征因子的重要性得分作为每个特征的权重系数，合成了月度投资网络搜索指数（Investment Network Search Index，INSI）。

表4 各因子重要性得分

1.3 模型建立

LSTM 模型最早由Hochreiter 和Schmidhuber 在1997年提出。由于能更好地记忆时间序列的长期依赖关系，因此被广泛用于处理序列信息。Phased-LSTM 模型是在基础模型上添加了新的时间门kt来扩展LSTM，该门的开启和关闭由具有一定频率范围的参数振荡控制。模型结构如图1所示，原文中的定义公式如下：

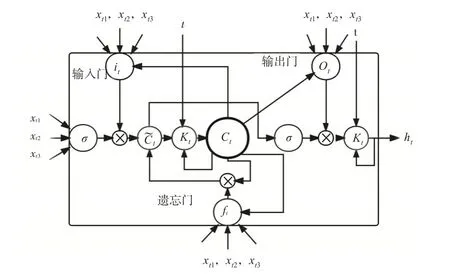
图1 MM-LSTM模型结构

其中，it、ft、ot分别为输入门、遗忘门、输出门的计算公式；°表示矩阵按元素相乘运算；xt和ht分别为输入特征向量和隐藏输出向量；σi、σf、σo、σc为激活函数；σh与权重矩阵W连接不同的输入门和记忆单元的输出；b为偏置项，是模型训练时要学习的参数。

与传统的LSTM 模型相比，Phased-LSTM 模型的更新可以在不规则的时间点tj上执行。本文用简写的cj=ctj表示储存记忆单元在tj时刻的状态，用cj-1表示储存记忆单元先前tj-1时刻的状态，则式（2）中ct和ht更新的方程为：

其中，cj只有在时间门打开的时候才允许更新，从而实现一个周期的一部分区间产生储存记忆单元的更新，这使得模型具备了处理不同频率数据的能力。本文合成的INSI为日度数据，ISI为月度数据，GDP_IG为季度数据，不同的模型需要的数据和数据频率存在差异。AR 模型仅利用GDP_IG自身的滞后性建模。MIDAS 模型虽然可以用多元高频数据来预测低频数据，但多元高频数据由于倍差较大，需要调整为同频的，本文把INSI降频为月度数据，记为INSI_M。MM-LSTM 模型能直接利用月度数据、日度数据对季度数据进行预测，有效地利用了混频数据的信息。

2 实证研究

2.1 基于AR模型的实证

AR 模型通过利用时间序列自身的滞后性，对未来指标的变动进行预测。利用该模型进行时间序列分析时，需要检验被研究的序列是否为平稳序列，以防止伪回归。本文采用EViews 10.0 对GDP_IG数据进行建模，根据AIC与SC 准则，其中添加截距项的未进行差分的序列通过平稳性检验，拒绝了存在单位根的原假设，序列平稳。同时，根据序列的自相关图和偏自相关图（图略）可知，自相关图呈现拖尾特征，偏自相关图呈现一阶截尾特征，因此应建立AR 模型。通过各种模型参数建模比较，根据AIC、SC、HQ值和回归方程各系数的显著性，最终确定应建立添加截距项的AR（1）模型。为了进行扩展预测，将样本内估计区间设置为2011 年第一季度至2020 年第四季度，样本外预测区间扩展到2022年第四季度①本文采用静态预测，每次向前预测一个数据，并且假设上一期的预测值等于真实值。。其中，样本内均方根误差为2.139，样本外均方根误差为5.708。

2.2 基于AR-MIDAS模型的实证

MIDAS 模型最初是由Ghysels 等在2004 年提出的，MIDAS 模型的显著特点是可以直接使用不同频率的数据进行建模。基础的MIDAS模型主要包括单变量和多变量MIDAS模型，以及加入自回归项的AR-MIDAS模型和h步向前预测的MIDAS 模型。因宏观经济运行的惯性作用，经济时间序列普遍存在自相关性，因变量的若干期会对当期产生影响，因此此处采用含有自回归的AR-MIDAS 模型。为了研究不同类型数据和不同MIDAS 模型预测差异，本文分别使用ISI和INSI_M数据建立单因素AR-MIDAS 模型，并同时使用以上两类数据建立双因素AR-MIDAS模型进行对比研究。

前文基于AR 模型的分析已经讨论了GDP_IG的滞后阶数，这里直接令AR-MIDAS模型的自回归项滞后阶数p=1。利用EViews 软件建模时，还需要确定高频回归器抽取的样本数和高频数据的滞后阶数。本文选取阿尔蒙多项式，软件可以根据AIC准则自动寻找高频回归器的最佳滞后阶数，这里最大滞后阶数设置为12，即高频回归器最多使用前12 个月的数据来拟合当前的GDP_IG数据。关于滞后阶数的选择，通过各种模型建模比较，根据回归方程各系数的显著性和样本区间内外的预测误差等参数最终确定。根据ISI建模得到的模型为AR（1）-MIDAS（4，2），模型的拟合优度为0.976，样本内均方根误差为0.910，样本外均方根误差为1.243。根据INSI_M建模得到的模型为AR（1）-MIDAS（3，0），样本内均方根误差为2.332，样本外均方根误差为5.350。结合ISI、INSI_M构建AR-MIDAS模型，为了保证各模型拟合效果和预测结果具有可比性，此处直接引用上述单因素AR-MIDAS建模的各种参数设置进行建模，记为AR（1）-MIDAS_tn。模型的样本内均方根误差为0.763，样本外均方根误差为1.212，其样本内外预测误差与单因素AR-MIDAS 模型相比均有所降低。

2.3 基于MM-LSTM模型的实证

通过上述AR模型、MIDAS模型可知，合成的ISI、INSI数据可以用于中国经济波动预测，这使得构建的MM-LSTM 模型具有理论基础。由于GDP_IG与ISI和INSI数据存在较大差异，对模型进行训练和测试之前，先对数据进行归一化处理。归一化公式如下：

其中，xi表示序列X中的第i个值，max(X)、min(X)分别表示序列X的最大值、最小值。与前面模型的样本内区间和样本外区间设置相同，2011—2020 年的数据作为训练集，2021—2022年的数据作为测试集。

（1）MM-LSTM模型参数设置

通过设置合适的参数，可以获得良好的深度学习性能，本文的目标是预测经济波动，故选用均方根误差（RMSE）作为损失函数。优化器方面，本文采用Adam 优化器进行优化训练。Adam 优化器是目前最常用的算法，与其他优化器相比，Adam算法收敛速度最快，学习效率更高。各网络层的激活函数均采用ReLu 函数，模型的最后一层采用线性linear 函数。为防止出现过拟合现象，对INSI数据设置Dropout层，网络节点的舍弃率设为0.2。

（2）MM-LSTM模型实证

为了与上文的MIDAS 模型进行对比研究，分别使用ISI、使用INSI以及同时使用ISI和INSI数据分开建模。三种模型分别记为MM-LSTM_t、MM-LSTM_n、MM-LSTM_tn。反复修改参数后，根据模型的训练集误差和测试集误差得到最优参数设置值，见表5。

表5 最优参数设置

表5 中，n_test表示测试集使用的月份数，epochs和batch_size分别代表模型训练时的迭代次数和一次训练所取的样本数，nodes代表隐藏神经元个数，month_t和month_p分别代表训练时使用当季和上一季的月份数量，gdp_p代表GDP_IG数据的滞后期数。以MM-LSTM_t模型为例，从表5 中的结果来看，其在预测当季的GDP_IG时，使用当季三个月和上季最后一个月的数据将取得相对较好的结果。

根据表5 还可以发现，使用ISI数据建立的模型训练集、测试集误差与使用INSI数据建立的模型误差都相对较小，这与MIDAS 模型的结果一致。原因可能是，ISI数据是由各宏观经济指标合成的，与经济波动直接相关；而INSI数据是根据与投资相关指标的搜索数据建立的联系，具有一定的不确定性。

由上述结果可知，使用混频数据的MM-LSTM模型训练集和预测集误差都最小。为了验证该模型是否具有提前预测GDP_IG数据的功能，将模型参数month_t分别设置为1、2、3。通过调整表5中其他参数得到模型的训练和测试误差，如表6所示。

表6 MM-LSTM_tn模型训练和预测误差比较

表6中，30+1表示使用每季度前30天的INSI数据和1 个月的ISI数据预测该季度的GDP_IG数据。对比发现，仅使用当季前30天和1个月数据就可以比国家统计局提前约60天预测该GDP_IG数据。而使用当季前60天和2 个月数据预测时其预测结果与AR-MIDAS 模型精度相当，但其可提前30天预测该GDP_IG数据。因此，可以利用这一预测的先行性，为政府部门制定经济政策提供决策依据。

3 模型预测效果评估

3.1 各模型预测性能比较

利用实证分析部分各模型的估计结果，计算各模型样本内拟合误差和样本外预测误差，如表7所示。

表7 各模型样本内外预测性能比较

第一，根据投资合成的INSI和ISI数据与GDP_IG序列之间存在正向关系，说明自2011年以来，较高的投资率是引起经济波动的重要因素，若想经济有较大的波动，则需要用适度的投资刺激我国经济，但同时应警惕过高的投资率所带来的GDP大幅度波动。

第二，从所有模型的估计结果来看，MIDAS 模型与MM-LSTM模型比仅利用GDP_IG数据的AR模型预测效果有所提高，说明本文合成的投资统计指数和投资网络搜索指数对中国经济波动的预测具有优化作用。其中，投资统计指数数据对经济波动的预测优化效果更好。但综合来看，预测经济波动取得了最好的效果。

第三，从使用混频数据估计结果来看，MM-LSTM 模型的样本内拟合误差和样本外预测误差比AR（1）-MIDAS模型的预测精度分别提高了3.5和38.4个百分点。究其原因，AR（1）-MIDAS 模型直接使用了月度投资统计指数数据，但把日度投资网络搜索指数数据降频为月度数据；而MM-LSTM 模型直接使用了月度数据和日度数据。这说明MM-LSTM模型更为有效地利用了样本信息，得到了更加精确的预测结果，同时也说明了MM-LSTM模型可以更好地拟合我国宏观经济波动。

第四，从使用投资网络搜索指数数据来看，MIDAS 模型和MM-LSTM模型在添加了投资网络搜索指数数据后，样本外预测误差分别比仅使用投资统计数据的样本外预测误差降低了3.1和52.2个百分点。这说明本文添加网络搜索数据提高了模型的估计精度。基于这一特点，本文认为网络搜索数据作为反映用户关注变化的即时指标，为传统的监测方法提供了有效补充，可以用来预测经济波动。

综上，从MM-LSTM模型和对比模型对中国宏观经济波动的预测结果可以看出，MM-LSTM 模型在中国宏观经济波动预测中的有效性得到了证实。

3.2 模型预测结果比较

从图2 来看，AR 模型对GDP_IG的估计结果类似于将原始值往后平移1 期，当GDP_IG出现较大波动时，不能及时预测。例如，2020年第一季度、2021年第一季度和2022年第二季度，预测结果出现了很大偏差。从下页图3来看，与AR模型相比，加入投资统计、网络搜索指数数据后，AR（1）-MIDAS-tn模型准确预测了2020年第一季度、2021 年第一季度和2022 年第二季度的波动，同时样本外短期预测效果较好，但2022 年第二季度波动预测误差较大。从下页图4 来看，MM-LSTM_tn 模型短期预测比MIDAS 模型更加准确，中期预测误差也相对较小，这说明本文提出的MM-LSTM 模型提高了样本外短期和中期的预测精度。

图2 AR模型样本内拟合和样本外预测结果对比

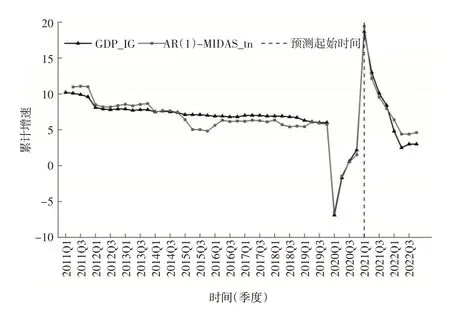
图3 AR(1)-MIDAS_tn模型样本内拟合和样本外预测结果对比

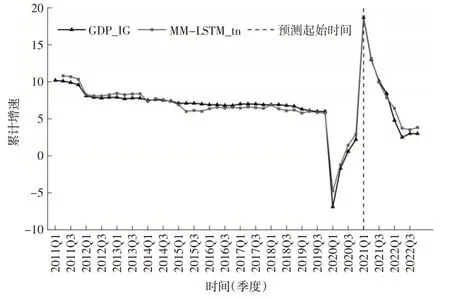
图4 MM-LSTM_tn模型样本内拟合和样本外预测结果对比

4 结论

实时、准确地预测我国经济波动是宏观经济研究中的重要课题。本文从宏观和微观两个层面分析了投资对中国经济增长的影响。考虑到宏观经济指标间并不都是同频数据，以及大量的网络搜索数据的有效性已得到学者们证实，本文构建了能够利用季度数据、月度数据和日度数据的多源MM-LSTM 模型。通过选择国内生产总值指数累计值（上年同期=100）数据和月度统计指标与网络搜索日度指标，本文从投资角度对我国2011年1月1日至2022年12月31日的经济波动进行了实证分析。本文的主要结论如下：

（1）投资相关指标与我国GDP_IG之间存在正向关系。加入投资统计指数或投资网络搜索指数的两种模型比基准模型的预测误差更小。这说明了用投资指标预测我国经济波动的可行性。

（2）添加投资网络搜索数据提高了模型的估计精度。MIDAS 模型和MM-LSTM 模型在加入投资网络搜索指数后，样本外预测误差分别降低了3.1和52.2个百分点，说明网络搜索数据对经济预测具有积极影响。

（3）MM-LSTM 模型具有更小的预测误差，提高了短期和中期的预测精度。本文构建的MM-LSTM 模型充分利用了混频数据的信息，与AR 模型、MIDAS 模型的最优结果相比，能够使样本内拟合误差降低3.5个百分点，样本外预测误差降低38.4 个百分点，并且准确预测了2020 年第一季度、2021 年第一季度、2022 年第二季度的波动，从而验证了模型的有效性。

（4）本文利用混频数据构建MM-LSTM模型对经济波动进行预测时，仅使用当季前30天和1个月数据就可以比国家统计局提前约60 天预测该季度GDP_IG数据，其预测精度高于AR模型。而使用当季前60天和2个月数据预测时，其预测结果与AR-MIDAS 模型精度相当，但其预测结果可提前30天预测该季度GDP_IG数据。可以利用这一预测的先行性，为政府部门制定经济政策提供决策依据。