拾级而上重本质，开拓进取升素养

熊洪智 刘勇 刘科兰

2023年全国数学新高考Ⅱ卷顺应高考命题改革，以素养为导向，通过创设多样命题情境，突出对数学关键能力的考查，充分发挥数学学科在人才选拔中的重要作用.

1深化基础考查，指向关键能力

《中国高考评价体系》指出，高考以能力为重、知识为基，关键能力是高考重要的考核目标，也是测试和评价的核心指标和因素.数学关键能力是指进入更高层次的学习者，在面对数学学科相关的生活实践或学习探索问题情境时，能有效地提出问题、认识问题、分析问题和解决问题所必须具备的能力.《中国高考评价体系》阐述了适合高考评价规律的三个方面关键能力群：以认识世界为核心的知识能力群、[JP+1]以解决实际问题为核心的实践操作能力群和涵盖了各种关键思维能力的思维认知能力群.在2023年全国数学新高考Ⅱ卷中，主要考查逻辑思维能力、运算求解能力、空间想象能力、应用实践能力和创新能力5项数学关键能力.

1.1逻辑思维能力

例1（第11题）若函数f（x）=alnx+bx+cx2（a≠0）既有极大值也有极小值，则（）.

A.bc>0

B.ab>0

C.b2+8ac>0

D.ac<0

评析：本题将导数与方程相结合，重点考查逻辑推理能力和化归与转化的数学思想方法，本题各选项之间有一定关联，可以由已知条件，经过分析与转化，通过一个思路来判断4个结论是否正确.对于函数极值问题的研究，主要转化为其导函数零点存在性问题，进而转化为方程根的分布问题，特别地，教学中要引导学生理解“函数的极值点——导函数零点——相应方程的根——导函数图象与x轴交点”这四者的关系及其应用.

1.2运算求解能力

例2（第8题）记Sn为等比数列{an}的前n项和，若S4=－5，S6=21S2，则S8=（）.

A.120

B.85

C.－85

D.－120

评析：本题源自人教A版选择性必修第二册第37页例9，例9是对数列Sn，S2n－Sn，S3n－S2n性质的证明，考查等比数列的求和公式及其性质，着重考查运算求解和逻辑思维能力.渗透了整体思想、方程思想、化归与转化思想，同时考查逻辑推理、数学运算等素养.

1.3空间想象能力

例3（第9题）已知圆锥的顶点为P，底面圆心为O，AB为底面直径，∠APB=120°，PA=2，点C在底面圆周上，且二面角P-AC-O為45°，则（）.

A.该圆锥的体积为π

B.该圆锥的侧面积为43π

C.AC=22

D.△PAC的面积为3

评析：本题以圆锥为载体，综合考查二面角、圆锥的体积和侧面积等知识.通过二面角P-AC-O为45°可以确定点C在底面圆周上的位置，根据圆锥的母线长为2可以求得圆锥的高和底面圆的半径，为后续的判断奠定基础.本题全面考查基础，四个选项设问逐次递进，各选项分别考查圆锥的不同性质，互相联系，突出对基础知识和基本概念的深入理解和灵活掌握.考查学生转化思想和空间想象能力.

1.4应用实践能力

例4（第19题）某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异，经过大量调查，得到如下的患病者和未患病者该指标的频率分布直方图（如图1）：

利用该指标制定一个检测标准，需要确定临界值c，将该指标大于c的人判定为阳性，小于或等于c的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率，记为p（c）；误诊率是将未患病者判定为阳性的概率，记为q（c）.假设数据在组内均匀分布，以事件发生的频率作为相应事件发生的概率.

（1）当漏诊率p（c）=0.5％时，求临界值c和误诊率q（c）；

（2）设函数f（c）=p（c）+q（c），当c∈［95，105］时，求f（c）的解析式，并求f（c）在区间［95，105］的最小值.

评析：试题以疾病的检测为背景进行设计，既有现实意义，也能很好地体现数学学科的应用价值.

第（1）问本质上是考查百分位数的运用，属于新教材新增内容，百分位数的引入，需要我们更进一步理解频率分别直方图中面积的含义；第（2）问要确定一个使得误诊率和漏诊率之和尽量低的临界值c，需要计算相应的矩形面积之和，最终结合分段函数的单调性计算最值.本题立意新颖，突出对学生应用实践能力和逻辑思维能力的考查.

1.5创新能力

例5（第12题）在信道内传输0，1信号，信号的传输相互独立.发送0时，收到1的概率为α（0<α<1），收到0的概率为1－α；发送1时，收到0的概率为β（0<β<1），收到1的概率为1－β.考虑两种传输方案：单次传输和三次传输.单次传输是指每个信号只发送1次，三次传输是指每个信号重复发送3次.收到的信号需要译码，译码规则如下：单次传输时，收到的信号即为译码；三次传输时，收到的信号中出现次数多的即为译码（例如，若依次收到1，0，1，则译码为1）.

A.采用单次传输方案，若依次发送1，0，1，则依次收到l，0，1的概率为（1－α）（1－β）2

B.采用三次传输方案，若发送1，则依次收到1，0，1的概率为β（1－β）2

C.采用三次传输方案，若发送1，则译码为1的概率为β（1－β）2+（1－β）3

D.当0<α<0.5时，若发送0，则采用三次传输方案译码为0的概率大于采用单次传输方案译码为0的概率

评析：本题源自人教A版选择性必修第三册第51页例6，以信号传输为情境考查二项分布及其应用.试题设计了单次传输和三次传输两种传输方式，考查学生利用概率加法公式及乘法公式求概率的能力及对新概念、新知识的理解和探究能力，考查分析问题和解决问题能力及创新应用能力.

2突出主干知识，构建完整体系

2023年全国数学新高考Ⅱ卷试题突出对六大主干知识的考查.如考查数列的题目有第8题、第18题；考查三角函数和解三角形的题目有第7，16，17题；考查立体几何的题目有第9，14，20题；考查概率统计的题目有第3，12，19题；考查解析几何的题目有第5，10，15，21题；考查函数知识的题目有第4，6，11，22题.因此，在复习备考中要关注主干知识，引领学生积累六大主干知识基本的数学活动经验，形成完整的知识体系.

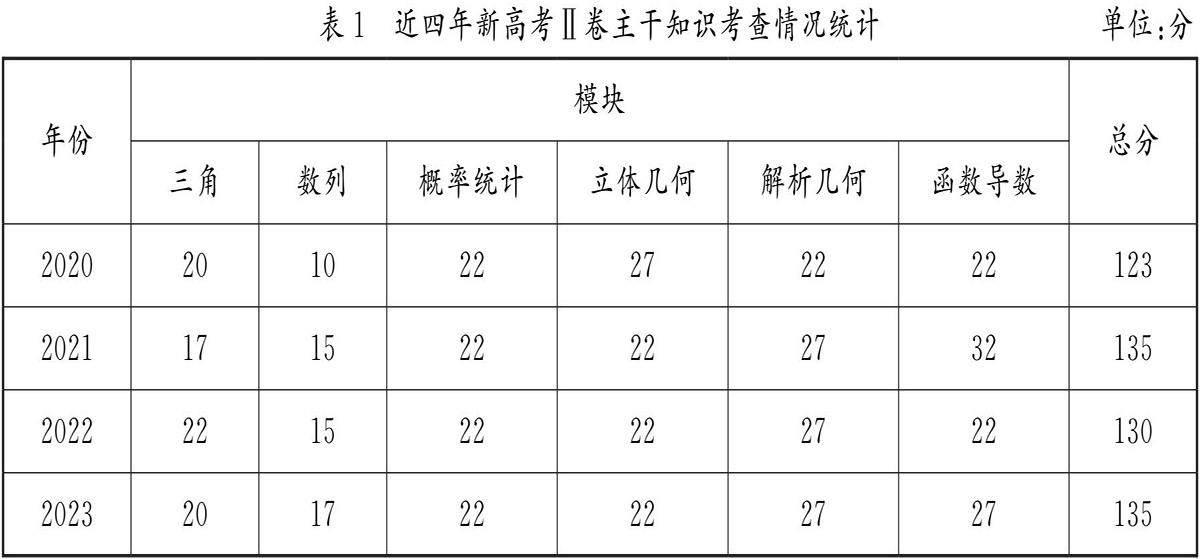
全面考查基础，并不是平均用力，而是突出考查支撑中学数学的核心知识.从表1可以看出，近四年全国数学新高考Ⅱ卷中都突出对六大主干知识的考查，力图让学生构建完整的基础知识体系，为将来发展奠定良好的基础.

3倡导通性通法，实现精准选拔

2023年新高考Ⅱ卷试题的求解入口宽、思路多样，体现通性通法，真实反映考生的基础理解水平，“反刷题”“反套路”，抑制“秒杀”，不提倡一知半解所谓的“高观点”.不同的理解水平在解题时间和准确性上的差异可以有效区分考生.

例6（第20题）如图2，三棱锥A-BCD中，DA=DB=DC，BD⊥CD，∠ADB=∠ADC=60°，E为BC的中点.

（1）证明：BC⊥DA；

（2）点F满足EF=DA，求二面角D-AB-F的正弦值.

评析：

本题以三棱锥这一常见的空间几何体为载体，第（1）问考查异面直线垂直的证明，可以利用“线面垂直线线垂直”，关键是直线与平面垂直的判定及直线与平面垂直的定义的应用，还可以用向量运算（数量积等于零）来证明（见解析）；第（2）问考查二面角的计算，可以采用坐标法、综合法和基底法求解，不同的解题方法能够反映学生对立体几何问题中通性通法的掌握情况.

4落实“四翼”考查，助力“双减”落实

2023年新高考Ⅱ卷紧扣中国高考评价体系对“四翼”考查的要求，试题注重考查学生对数学基础知识的理解和掌握，重视教考衔接.

（1）注重基础性要求

试卷在选择题、填空题中全面考查复数、集合、平面向量、三角函数、排列组合、几何体体积等基础知识.在解答题中也深入考查基础，强调学生对数学基础知识和基本思想方法的灵活运用.

（2）彰显综合性要求

试题在体现基础性的同时也重视对综合性的考查，要求考生能运用所学知识将复杂的问题情境进行分解，合理选择解题方法加以解决，充分体现高考命题从知识立意、能力立意到素养立意的转变.高考数学试题的综合性一方面是数学学科内部各个主题的综合，另一方面是数学学科和其他学科的交汇融合.

例7（第22题）（Ⅰ）证明：当0

（Ⅱ）已知函数f（x）=cosax－ln（1－x2），若x=0是f（x）的极大值点，求a的取值范围.

评析：本题第（1）问起点低，只需通过作差构造函数，并借助导数的工具作用判断新函数的单调性，即可求解；试题第（2）问涉及的概念和性质很基本，但是考查很深入，为考生解答问题提供了广阔的发挥空间.本题命题角度新颖，淡化考试技巧，仍考查通性通法，但是对考生的逻辑推理素养和分析解决问题能力要求较高，较好地体现了试题的选拔功能.

（3）凸显应用性要求

数学源自生活、生产实践，归宿于解决实际问题.在应用数学知识、思想和方法解决实际问题的过程中发展学生的数学建模、数据分析、数学运算等素养，引导学生重视数学应用，增强学以致用的意识.

例8（第3题）某学校为了解学生参加体育运动的情况，用比例分配的分层随机抽样方法作抽样调查，拟从初中部和高中部两层共抽取60名学生，已知该校初中部和高中部分别有400名和200名学生，则不同的抽样结果共有（）.

A.C45400·C15200种

B.C20400·C40200种

C.C30400·C30200种

D.C40400·C20200种

评析：本题以单选题的形式考查分层随机抽样及排列组合的内容，以学校了解学生参加体育运动的情况为命题背景，取材于学生生活中的实际问题，考查学生的数学运算与数学建模素养，通过问题的解决引导学生对数学产生浓厚的学习兴趣，并积极应用数学研究实际问题.

（4）体现创新性要求

试题的灵活性和答案的开放性，体现了新高考从重点考查知识技能到重点考查思维能力的转变，表明数学教学应从灌输知识、重复练习到培养数学思维能力、数学核心素养的转变，开放性试题不仅考查学生运用数学思维理解和解决问题的能力，还考查学生的核心素养及创新能力.

例9（第15题）已知直线l：x－my+1=0与⊙C：（x－1）2+y2=4交于A，B两点，写出满足“△ABC面积为85”的m的一个值＿＿＿＿.

评析：本题是一道开放题，在体现开放性的同时考查学生思维的有序性.在内容方面，综合考查直线和圆的位置关系、点到直线的距离公式、圆的内接三角形性质等，属于在知识点的交汇处命题，体现了新高考命题的创新性要求.

5教学建议

针对2023年新高考Ⅱ卷数学试题“综合性强，能力要求高，解题方法活”这些新特点，在高三复习教学中，教师要坚持把能力培养作为首要任务，通过教学方式和方法的创新，改变机械刷题与套路训练模式，提升学生的核心素养.

（1）夯实基础知识，回归教材本质

本套试卷注重对基础知识和基本能力的考查，试卷第1，2，3，4，7，13，14题皆为基础题；本套试卷充分体现了考教结合，如第7，8，10，12，17，18，22（1）题均源自教材而高于教材.因此，在高三复习备考中我们应注重基础，回归教材，注重“依标靠本”，切忌盲目、随意扩展知识内容.当然，立足教材并不是对教材内容的简单重复，而是对教材内容进行二次重构，特别是对教材中的一些典型问题，围绕主干知识，深入挖掘教材例题、习题的价值，通过一题多解、一题多变、多题一解等高階思维活动，剖析问题的数学本质，帮助学生夯实基础，提升解决问题的能力.

（2）关注知识生成，强调融会贯通

在复习备考中要引导学生明确知识的发生、发展过程，揭示知识的内在联系，帮助学生构建完整的知识体系，关注不同知识之间的联系，引导学生整合各个知识点，形成完整的学科知识框架和思想方法体系，促进知识间的融会贯通.

（3）注重思想渗透，促进素养达成

数学思想方法是数学学科的精髓，是数学素养的重要内容之一.本套试卷注重对数学思想方法的考查.比如，第5，9，16，19，20题都体现了数形结合思想方法在解决问题中的优越性；第11，21，22题体现了化归与转化的思想方法；第8，18，22题体现了分类讨论的思想方法.因此，在复习备考中，要注意数学思想方法的渗透，充分挖掘由数学基础知识所体现出来的数学思想方法，平常可以专门设置习题训练，引导学生根据实际题目内容选择不同的数学思想方法，使其灵活使用数形结合、分类讨论、函数与方程、特殊与一般、转化、正难则反等多种数学思想方法，帮助他们积累更多的解题经验，提升数学解题能力和数学核心素养.

（4）重视思维培养，提升关键能力

学生在面对综合性较强的问题与新颖、较为复杂的情境时，需要具有一定的探究能力与创新精神，以及较好的数学素养和优秀的思维品质.在复习课中，要摈弃传统的“教师满堂灌—学生记笔记—课后题海战术”的复习模式，在课堂上采用回归教材例习题、引导学生自主编题、学生说题、绘制思维导图等方式提升课堂效率，促进学生将知识和方法内化为自身的知识结构，巩固所学知识，强化数学思维，为综合能力的提升奠定基础.