利用“瓜豆原理”模型分析轨迹问题

陈礼弦

摘要：文章立足于初中数学教学实践，针对轨迹问题这一中考难点，利用“瓜豆原理”模型巧妙分析轨迹问题的求解思路，目的在于帮助初中数学教师及学生找到应对轨迹问题的正确思路，提高学生分析问题和解决问题的能力，进而提升其数学核心素养.

关键词：初中数学；轨迹问题；“瓜豆原理”模型

中图分类号：G632文献标识码：A文章编号：1008-0333（2024）11-0017-03

在初中数学教学中，轨迹问题是教学的难点，也是核心素养重点考查对象.根据笔者多年的教学经验，引导学生弄清楚“瓜豆原理”模型，利用其分析轨迹问题，会收到事半功倍的效果.

“瓜豆原理”是一种数学问题的形象描述，即若两动点到某定点的距离比是定值，夹角是定角，则两动点的运动路径相同.其中，主动点叫作“瓜”，从动点叫作“豆”.如果“瓜”在直线上运动，那么“豆”的运动轨迹也是直线；如果“瓜”在圆周上运动，那么“豆”的运动轨迹也是圆.这种主从联动轨迹问题被称为“瓜豆原理”或“瓜豆模型”，在某一个特殊位置，就是我们要解决的轨迹问题[1].

1 模型一动点在直线上运动

这类问题的基本特点是主动点在直线上运动，从动点的运动轨迹也是直线.其结论主要有两个：一是主动点和从动点所在直线的夹角是一个定值；二是主动点和从动点轨迹长度之比值是一个定值.

1.1 模型分析

例1如图1，G为线段EF一动点，D为定点，连接DG，取DG中点H，当点G在EF运动时，画出点H的运动轨迹.

解析如图2，线段IJ即为点H运动的轨迹，理由如下：连接DE，DF.因为当点G在点E处时，点H在点I处，当点G在点F处时，点H在点J处，所以点I是DE的中点，点J是DF的中点，所以IJ∥EF，所以IJ=12EF， 所以IJEF=12，所以在运动过程中，主动点G和从动点H所在的直线DG和DH的夹角是0°（定值），主动点G和从动点H的轨迹长之比值是12（定值）.从而可知主动点G运动的轨迹是线段，从动点H运动的轨迹也是线段.

例2如图3，△DEF是等腰直角三角形，∠EDF=90°且DE=DF，當点E在线段MN上运动时，画出点F的运动轨迹.

解析如图4，线段F′F″即为点F的轨迹. 取点F的起始位置F′和终点位置F″，连接即得点F轨迹为线段F′F″.因为主动点E和从动点F所在直线DE和DF的夹角为90°，易证△MND≌△F′F″D，主动点E和从动点F的轨迹长之比值等于MN∶F′F″=1，所以点E、F的轨迹是同一图形.

1.2 模型应用

例3如图5，矩形DEFG中，DE=3，DG=4，点H在边DG上且DH∶HG=1∶3.动点I从点D出发，沿DE运动到点E停止.过点H作HK⊥HI交射线EF于点K，设J是线段HK的中点.求在点I运动的整个过程中，点J运动的路径的长.

解析如图6，当I与D重合时，点K与K′重合，此时点J在J′处，当点I与E重合时，K与K″重合，点J在J″处，点J的运动轨迹是线段J′J″.因为DG=4，DH∶HG=1∶3，所以DH=1，HG=3.在Rt△DEH中，DH=1，DE=3，所以HE=DH2+DE2=1+9=10.因为DG//EF，所以∠DHE=∠HEK″，又因为∠D=∠EHK″=90°，所以△DHE～△HEK″，所以HEEK″=DHHE，所以EK″=10×10=10.又因为EK′=DH=1，所以K′K″=EK″-EK′=9，所以J′J″=12K′K″=92，所以点J的运动路径的长为92.

2 模型二动点在圆周上运动

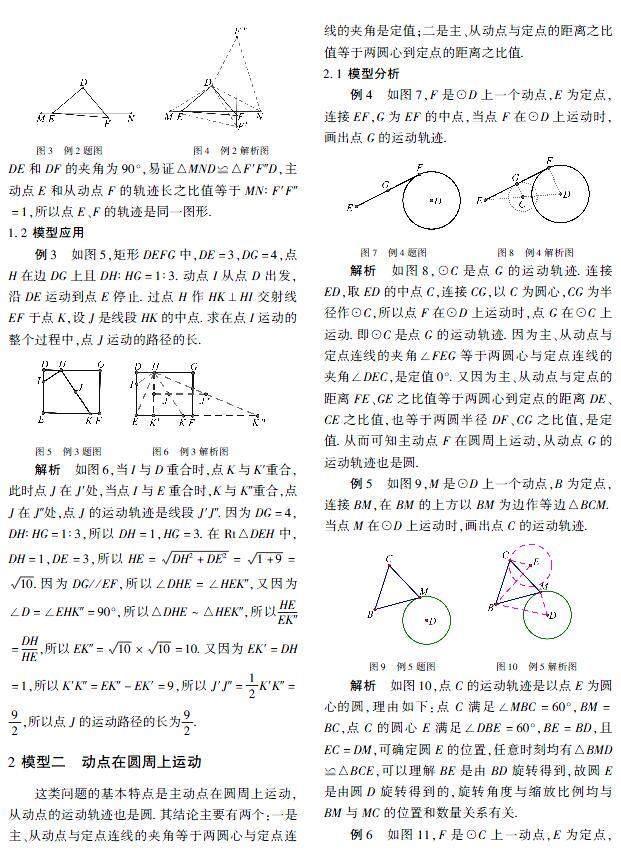
这类问题的基本特点是主动点在圆周上运动，从动点的运动轨迹也是圆.其结论主要有两个：一是主、从动点与定点连线的夹角等于两圆心与定点连线的夹角是定值；二是主、从动点与定点的距离之比值等于两圆心到定点的距离之比值.

2.1 模型分析

例4如图7，F是⊙D上一个动点，E为定点，连接EF，G为EF的中点，当点F在⊙D上运动时，画出点G的运动轨迹.

解析如图8，⊙C是点G的运动轨迹.连接ED，取ED的中点C，连接CG，以C为圆心，CG为半径作⊙C，所以点F在⊙D上运动时，点G在⊙C上运动.即⊙C是点G的运动轨迹.因为主、从动点与定点连线的夹角∠FEG等于两圆心与定点连线的夹角∠DEC，是定值0°.又因为主、从动点与定点的距离FE、GE之比值等于两圆心到定点的距离DE、CE之比值，也等于两圆半径DF、CG之比值，是定值.从而可知主动点F在圆周上运动，从动点G的运动轨迹也是圆.

例5如图9，M是⊙D上一个动点，B为定点，连接BM，在BM的上方以BM为边作等边△BCM.当点M在⊙D上运动时，画出点C的运动轨迹.

解析如图10，点C的运动轨迹是以点E为圆心的圆，理由如下：点C满足∠MBC=60°，BM=BC，点C的圆心E满足∠DBE=60°，BE=BD，且EC=DM，可确定圆E的位置，任意时刻均有△BMD≌△BCE，可以理解BE是由BD旋转得到，故圆E是由圆D旋转得到的，旋转角度与缩放比例均与BM与MC的位置和数量关系有关.

例6如图11，F是⊙C上一动点，E为定点，连接EF，以EF为斜边在EF上方作等腰直角三角形EFD.当点F在⊙C上运动时，画点D的轨迹.

解析如图12，点D的轨迹为以点G为圆心，22CF长为半径的圆.D点满足∠FED=45°，EF：ED=2∶1，故D点轨迹是一个圆.连接EC，构造∠GEC=45°且EC∶EG=2∶1.G点即为D点轨迹圆圆心，此时任意时刻均有△ECF∽△EGD.即可确定点D的轨迹圆.所以点D的轨迹为以点G为圆心，22CF长为半径的圆.

2.2 模型应用

例7如图13，⊙E的直径BC=4，D为⊙E上的动点，连接BD，F为BD的中点，若点D在圆上运动一周，求点F经过的路径长.

解析如图14，因为主、从动点与定点连线DB、FB的夹角等于两圆心与定点连线EB、GB的夹角，且是0°，为定值，又因为主、从动点与定点的距离DB、FB之比值等于两圆心到定点的距离EB、GB之比值，也等于两圆半径EB、GB之比值，是定值12.所以是点D在⊙E上运动，点F的运动轨迹也是圆.

如图14，当点D在点C处时，点F在点E处，当点D在点B处时，点F在点B处，所以EB是这个圆的直径，这个圆是⊙G.又因为BC=4，所以EB=2，所以GB=1，所以r=1，所以⊙G的周长为2πr=2π，所以点F经过的路径长是2π.

例8如图15，FG=3，⊙F的半径为1，E为⊙F上的动点，连接EG，在EG上方作一个等边三角形EGH，连接FH.求FH的最大值.

解析如图16，以FG为边在FG上方构造等边三角形△FGI，连接IH，以点I为圆心，IH为半径作圆I.因为主、从动点与定点连线EG、HG的夹角等于两圆心与定点连线FG、IG的夹角，且是60°为定值.又因为主、从动点与定点的距离EG、HG之比值等于两圆心到定点的距离FG、IG之比值，也等于两圆半径FE、IH之比值，是定值1.因为∠FGE=60°-∠EGI，∠IGH=60°-∠EGI，所以∠FGE=∠IGH.又因为FG=IG，EG=HG，所以△FGE≌△IGH，所以IH=FE=1.从而可知点H运动的轨迹是以点E为圆心、1为半径的圆，当F、I、H三点共线且H在FI的延长线上时，FH的最大值为FI+IH=3+1=4，此时点H在点H′处.

3 结束语

在解决轨迹问题时，要结合图形进行分析，主动点和从动点运动的轨迹是否属于“瓜豆原理”.如果主动点和从动点运动的轨迹属于“瓜豆原理”，就可以利用主动点在直线上运动，从动点的运动轨迹也是直线或主动点在圆周上运动，从动点的运动轨迹也是圆解决轨迹问题[2].

参考文献：

［1］ 熊长菊，张进.例谈瓜豆原理中动点轨迹最值问题的求解策略[J].数理化学习（初中版）， 2022（6）：5-9.

[2] 丁羽.初三学生动点轨迹问题的解决障碍及教学对策研究[D].广州：广州大学，2022.

［责任编辑：李璟］