降雨和库水位升降条件下考虑非饱和渗透系数空间变异的边坡可靠度分析

柳伟 徐长节 胡世韬 朱怀龙

DOI： 10.11835/j.issn.2096-6717.2023.034

收稿日期：2022?11?28

基金项目：国家杰出青年科学基金（51725802）；江西省交通运输厅科技项目（2021H0037）

作者简介：柳伟（1979- ），男，博士生，副教授，主要从事岩土力学试验和边坡分析研究，E-mail：jxlw1979@163.com。

通信作者：徐长节（通信作者），男，教授，博士生导师，E-mail：xucj@zju.edu.cn。

Received： 2022?11?28

Foundation items： The National Science Found for Distinguished Young Scholars （No. 51725802）; Science and Technology Project of Jiangxi Provincial Department of Transportation （No. 2021H0037）

Author brief： LIU Wei （1979- ）， PhD candidate， associate professor， main research interests： geotechnical mechanical tests and slope analysis， E-mail： jxlw1979@163.com.

corresponding author：XU Changjie （corresponding author）， professor， doctorial supervisor， E-mail： xucj@zju.edu.cn.

（1. 華东交通大学 江西省岩土工程基础设施安全与控制重点实验室，南昌 330013； 2. 江西交通职业技术学院，南昌 330013； 3. 浙江大学 滨海和城市岩土工程研究中心，杭州 310058； 4. 上海大学 力学与工程科学学院，上海 200444）

摘要：降雨和水位升降对库岸边坡具有显著影响，传统确定性分析难以准确评估其稳定性。考虑降雨和水位升降联合作用下水力参数的空间变异性，进行非饱和土边坡可靠度分析具有重要意义。以赣江库区中的莒洲岛边坡为研究对象，以贝叶斯方法校准的多元水力参数的联合随机场为基础，建立非饱和土边坡的稳定性分析方法。根据有限的岩土力学室内试验数据，采用贝叶斯方法校准土水特征曲线的模型参数，并从VGM、VGB、VG和FX模型中选出最优模型；联合多元水力参数的随机统计特征，生成非饱和土边坡渗透系数的随机场空间分布；针对2021年5月赣江水位快速升降并伴随暴雨的工程背景，将上述方法应用于莒洲岛库岸边坡的稳定性分析。研究结果表明，暴雨与水位变化的联合作用对边坡安全系数的影响显著，确定性分析的边坡安全系数偏低，考虑非饱和渗透系数空间变异性后计算所得到的SWCC综合可靠指标不能满足规范要求，需采取额外的边坡工程加固措施以保证边坡的长期稳定性。

关键词：库岸边坡；土水特征曲线；非饱和渗透系数；贝叶斯方法；可靠度分析

中图分类号：TU43     文献标志码：A     文章编号：2096-6717（2024）03-0061-12

Reliability analysis by considering spatial variability of unsaturated hydraulic conductivity under rainfall and reservoir water level fluctuation

LIU Wei^1，2， XU Changjie^1，3， HU Shitao⁴， ZHU Huailong^1，2

（1. Jiangxi Key Laboratory of Infrastructure Safety Control in Geotechnical Engineering， East China Jiaotong University， Nanchang 330013， P. R. China； 2. Jiangxi V&T College of Communications， Nanchang 330013， P. R. China； 3. Research Center of Coastal and Urban Geotechnical Engineering， Zhejiang University， Hangzhou 310058， P. R. China； 4.School of Mechanics and Engineering Science， Shanghai University， Shanghai 200444， P. R. China）

Abstract： The geotechnical parameter of soil mass in colluvial landslide is uncertain. Saturated hydraulic conductivity and soil-water characteristic curve （SWCC） are important parameters for the unsaturated seepage analysis. It is of great significance to carry out the reliability analysis of reservoir bank landslide considering the spatial variability. In this study， the Jvzhoudao slope in the Ganjiang Reservoir Area is investigated as a case. Firstly， according to the limited laboratory test data of saturation-matrix suction， the statistical characteristics of the SWCC properties， such as VGM， VGB， VG， and FX model parameters are calibrated by the Bayesian method， and the applied probabilities of SWCC model combination are determined by the laboratory measurements. Secondly， combining the random field characteristics of the saturated hydraulic conductivity with the random characteristics of the SWCC models， spatial distributions of the unsaturated hydraulic conductivity are generated in the slide body. Finally， for the extreme conditions in the Ganjiang Reservoir Area in May 2021， the proposed method was applied to the case stability analysis. Results indicate that the combined effect of rainstorm and water level change has a significant impact on the safety factor， and that the safety factor of the deterministic analysis is low. Reliability index calculated after considering the spatial variability of the unsaturated permeability coefficient cannot meet the specification requirements， while additional slope engineering reinforcement measures should be taken to guarantee the long-term stability of the slope.

Keywords： reservoir bank slope； soil-water characteristic curve； unsaturated hydraulic conductivity； Bayesian method； reliability analysis

地區强降雨以及库水位升降对边坡的稳定性有显著影响^[1]，同时非饱和土体在遇到降雨等湿化条件下可能会产生破坏^[2]。传统的确定性分析假设岩土参数在研究范围内为定值且服从均匀或线性分布，不能准确评估复杂工况下库岸边坡的稳定性。因此，基于非饱和土渗流理论和不确定性原理的边坡稳定性分析已成为学术和工程领域的热点和重点。

土水特征曲线SWCC（Soil-Water Characteristic Curve）表示土体水吸力随土体含水率的变化，反映了土壤水分能量和数量之间的关系，饱和渗透系数决定了水分入渗的难易程度，是研究边坡稳定性的重要水力参数，相关不确定性研究已取得一定的成果。唐栋等^[3]研究了不同工况下土水特征曲线的模型参数对渗流过程以及安全系数的影响，研究结果表明基质吸力对边坡安全系数具有明显的影响。王林等^[4]基于土水特性试验，采用贝叶斯比选方法对SWCC模型进行了参数校准。叶云雪等^[5]基于室内饱和土的各向等压压缩和土的收缩试验，提出了一个脱湿路径下低吸力段SWCC的预测方法。基于较为成熟的岩体结构规律，已有SWCC模型的有效性已得到了验证^[6]。潘振辉等^[7]针对压实黄土展开了压泵试验、变水头渗透试验和SWCC试验，探究了压实黄土微结构、饱和渗透系数和SWCC之间的影响和机制。丁小刚等^[8]提出了能够考虑压实作用影响的膨胀土SWCC曲线的双参数预测模型。Huang等^[9]考虑了土的应变软化效应，并基于非饱和土强度准则分析了渗流场对非饱和土边坡的影响。金磊等^[10]基于离散元法建立了三维随机孔隙结构模型，通过引入三维格子Boltzmann方法从孔隙尺度对渗流展开模拟。李梦姿等^[11]采用部分剪断Fredlund强度理论拉应力区强度包线的方法，提出了渗流作用下，无限边坡的稳定性分析方法。蒋水华等^[12]通过修正Green-Ampt入渗模型，探讨了岩土参数的空间变异性对非饱和土渗流边坡的影响。

目前根据有限的试验数据条件校准水力参数的随机场统计特征的研究涉及较少。基于此，笔者基于土水特性试验，采用贝叶斯方法校准了SWCC模型参数，并对比了不同模型对新干红黏土的适用性，在降雨以及水位升降条件下，使用随机场理论描述边坡上覆土的非饱和渗透系数，最后联合随机（场）统计特征，讨论非饱和渗透系数的空间变异性对边坡稳定性的影响。

1 非饱和土库岸边坡的稳定性分析

1.1 水力参数随机场理论

在工程地质环境中，由于矿物组成、沉积环境和固结历史等差异，处于不同空间的土体结构不尽相同，从而导致边坡的饱和渗透系数具有较大的不确定性。随机变量理论无法考虑饱和渗透系数的空间变异性，而随机场理论能够描述饱和渗透系数的空间分布，因此采用随机场理论描述边坡上覆土的岩土参数空间变异性。变异函数能够描述饱和渗透系数的空间变异性。如存在大量的饱和渗透系数原位勘查数据，变异函数样本值即可通过式（1）计算。 （1）

式中：为滞后距；为在两点之间用来计算变异函数的数据样本集。

常用的理论变异函数模型有球状模型、高斯模型和指数模型。采用具有简洁性和鲁棒性的球状变异函数^[13]（2）

式中：为块金值；为基台值；为变程。而实际上，变异函数是未知的，通常需要基于样本数据回归拟合得到。

饱和渗透系数k_s在三维空间中的各向异性统计特征，可由加权的滞后距h表示。 （3）

式中：分别为第1变程、第2变程和第3变程。通过随机场序贯高斯离散方法，能够生成饱和渗透系数k_s的空间分布，并将饱和渗透系数作为材料参数输入到数值模型中，即滑体中的每一个上覆土单元都会生成一個对应的饱和渗透系数k_s。

1.2 非饱和土边坡可靠度分析

1）瞬态渗流

在非饱和土中，孔隙水压力在应力场中的瞬态控制方程一般采用Richards^[14]提出的瞬态流动控制方程      （4）

式中：为非饱和土在方向上的非饱和渗透系数，其大小由基质吸力决定^[15]；为总水头；为渗流过程的时间；为水头边界流量；为水的重度；为非饱和土的容水性，由式（5）定义。 （5）

首先，通过土水特性试验和贝叶斯参数校准方法，得到土体的SWCC曲线，并求出式（5）中的；其次，通过饱和渗透试验得到饱和渗透系数；然后，通过饱和渗透系数和SWCC曲线的关系，得到非饱和土渗透系数；再者，通过对边界条件的设置得到总水头H和边界流量q的取值；最后，将上述条件代入式（6）即可求解偏微分方程。

2）非饱和土抗剪强度

饱和度、基质吸力以及非饱和渗透系数能够直接影响边坡土单元的总应力和孔隙水压力，进而影响非饱和土的抗剪强度和土条的抗剪强度，最后影响边坡的安全系数。    （6）

式中：为有效黏聚力；为有效内摩擦角；为总应力。需要说明的是，在实际工程中，有效黏聚力和有效内摩擦角也会受到孔隙水压力、渗透系数等因素的影响。只研究水力参数的空间变异性对边坡稳定性的影响，因此，不考虑基质吸力对有效黏聚力和有效内摩擦角的改变及其带来的影响。

3）安全系数计算

渗流作用下非饱和土边坡的安全系数，采用Morgenstern-Price极限平衡法^[16]，公式为 （7）

式中：为土条的非饱和抗剪强度；为土条的自重；和为土条的水平条间力；和为土条i的竖向条间力；为土条的边坡倾斜角；为土条的滑弧长度^[17]。

4）SWCC模型综合性的边坡安全系数

首先，使用岩土工程有限元软件GeoStudio2012对边坡进行有限元建模，通过改变每一个土体单元的材料参数，实现非饱和渗透系数随机场；然后，采用M-P极限平衡法计算边坡的安全系数；最后，采用蒙特卡洛模拟算法，计算100 000次边坡安全系数，并统计得到边坡的失效概率以及可靠指标。在蒙特卡洛模拟中，边坡的极限状态函数可表示为 （8）

式中：为临界滑动面的安全系数；为极限状态函数发生的概率，即失效概率。

采用MATLAB软件对每一个SWCC模型，随机生个样本和相应的SWCC曲线。利用饱和渗透系数在空间随机场中的离散值，计算出非饱和渗透系数的空间随机场。然后将非饱和渗透系数的空间随机场作为材料参数输入到模型中，最后计算得到个边坡安全系数值，同时统计SWCC模型中安全系数的均值和标准差。

根据SWCC模型参数的后验分布函数以及SWCC模型备选概率，通过式（9）计算出单一模型下边坡的失稳概率，通过式（10）计算考虑SWCC模型不确定性的边坡失稳概率。 （9） （10）

统计计算所得到的安全系数的均值以及方差Var[F_s|M_j，Z_b，k_w|]，分别表示为 （11） （12）

式中：和为模型、参数值相应安全系数的平均值和方差。

SWCC模型的不确定性以及对应模型参数的不确定性是分析边坡可靠度的关键。通过方差来表征每一个模型对边坡安全系数的相对贡献^[18]。以土水特征曲线土工试验数据为条件的总方差写     （13）

式中：和分别为给定SWCC模型、土工试验数据和固定饱和渗透系数时，安全系数的条件方差和期望值。是给定土工试验数据和固定饱和渗透系数的安全系数的综合条件期望值，可写为 （14）

式（13）中为边坡安全系数在备选SWCC模型下条件方差的平均值；为条件期望方差的平均值。两者量化了不同模型参数所引起的方差以及不同SWCC模型引起的方差。SWCC模型的相对贡献以及模型参数不确定性的相对贡献分别表示为 （15） （16）

非饱和土边坡可靠度分析的流程图如图1所示。首先根据室内试验数据，采用贝叶斯方法校准SWCC模型参数，并计算SWCC模型的备选概率；其次，采用随机场理论，计算饱和渗透系数在边坡中的空间分布；然后，联合SWCC模型的校准结果和饱和渗透系数的空间分布，计算非饱和渗透系数的空间分布；最后，采用子集蒙特卡洛模拟计算边坡的可靠指标，评估莒洲岛边坡的稳定性。

2 SWCC模型参数校准的贝叶斯方法

基于土水特性试验和SWCC模型的先验信息，采用贝叶斯理论，校准了不同的模型参数；根据饱和渗透系数的空间分布特征，生成边坡上覆土體单元的非饱和渗透系数的空间随机场。

2.1 SWCC模型参数校准的贝叶斯方法

对莒洲岛红黏土进行土水特性试验以获取SWCC试验数据。每一次试验都会设定一个不同的基质吸力，然后测试得到该条件下对应的饱和度。由于存在试验误差和模型误差，在处的试验结果与不同SWCC模型计算出的预测值也有所不同，和之间的差异可用误差表示。 （17）

假设和之间的误差服从均值为0，标准差为的正态分布^[16]。并且分别选取VGM 模型、VGB模型、VG模型和FX模型作为备选模型^[19-22]，则模型的个数为=4。SWCC模型对应的参数集可表示为。

采用联合均匀分布的方式构建SWCC模型的先验概率密度函数，以此表征在没有引入试验数据时模型参数的可用信息。采用相关文献中常用的取值范围，作为描述参数先验信息^[4]。以FX模型为例，将模型参数的先验概率密度函数表示成的联合均匀分布，即 （18）

式中：

表示SWCC模型的先验概率。当先验信息不足时，一般将各种模型的先验概率假定为同一值，即。因备选模型的数量=4，所以每一个备选模型的先验概率均为=0.25。

似然函数能够反映一组指定参数下的SWCC模型相较于试验数据的拟合程度，具体表示为       （19）

式中：为使用数学软件拟合得到的土水特征曲线，表示参数为的SWCC模型对试验数据的概率密度函数值。采用联合均匀分布描述SWCC模型参数的先验信息。已知的参数取值范围如表1所示^[23-24]。

根据先验概率和试验结果的数据集，可以将模型参数集的不确定性表示为对应的后验概率密度函数。     （20）

式中：，是独立于的归一化常数，表示试验数据在给定模型条件下的概率密度函数值。先验分布和似然函数可以分别由式（18）和式（19）计算。

后验分布的形式复杂且涉及高维积分问题。MCMC（Markov Chain Monte Carlo）模拟方法能够使抽样分布随模拟的进行改变，相比于蒙特卡洛模拟方法，其优点在于拥有更快的抽样速度。此外，这种做法能够避开直接求解复杂的后验概率密度函数，进而解决后验分布困难的理论计算问题^[25]。

采用M-H（Metropolis-Hastings）算法^[26]生成服从后验分布的MCMC随机参数集作为多元随机变量的数据，采用Gaussian Copula构建参数的多元联合概率密度函数，最后计算的后验分布^[3]。将土工试验数据代入到贝叶斯定理中，用后验概率量化SWCC模型的不确定性。    （21）

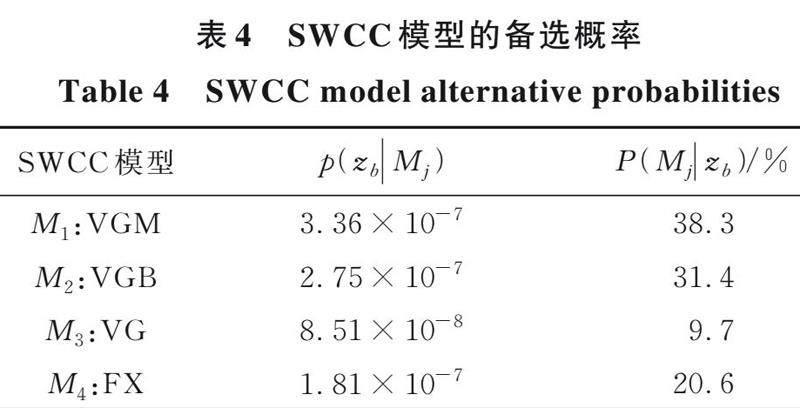
式中：SWCC模型的备选个数为4个，所以先验概率=0.25，是模型的归一化常数。根据式（21）可计算得到每一个SWCC模型的备选概率，一个SWCC模型的备选概率能够表征该模型对试验数据的适用性。

2.2 校准SWCC模型参数

对于土水特征曲线的低吸力段部分，采用GSTS型压力板仪获取试验数据；对于土水特征曲线的高吸力段部分，采用蒸汽平衡法获取试验数据。莒洲岛红黏土3个压实样的详细试验方案和数据如表2所示，试验数据点如图2所示。

首先，采用MCMC模拟算法为每一个SWCC模型随机生成组模型参数样本。然后，用M-H算法快速生成服从后验分布的模型参数样本集，并收敛到稳态的Markov Chain。最后，根据得到的样本统计出参数的后验分布特征，包括均值、标准差、相关系数等。

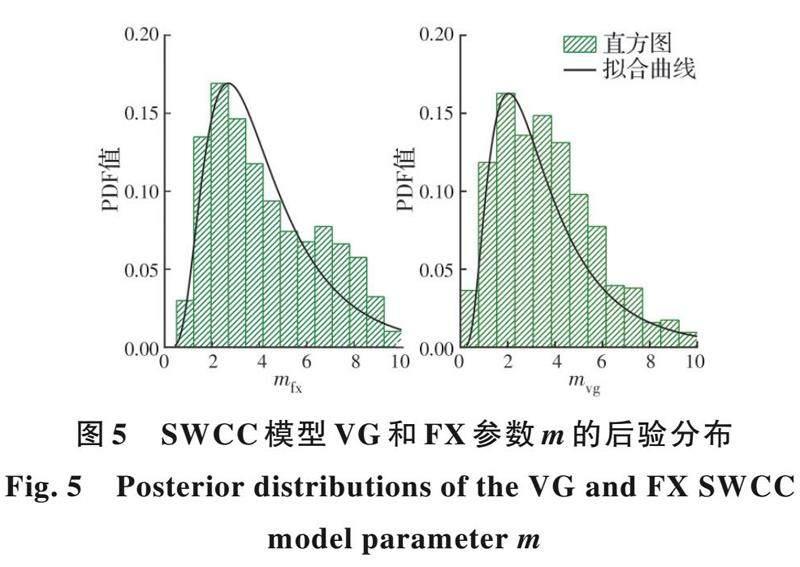
为了获得模型参数的后验分布，使用R语言编写贝叶斯校准方法的程序，将室内土工试验的结果数据、不同模型的先验信息输入到程序中，即可获得模型参数的后验分布。图3～图5给出了组MCMC随机样本统计的后验概率密度函数。图3表示模型参数的频数分布和概率密度函数PDF（Probabilistic Density Function），绿色直方图表示SWCC模型参数的频数分布，黑色曲线表示对应的PDF曲线。

表3表示4个SWCC模型参数的后验分布统计特征。其中，最大似然值表示后验分布最大值对应的模型参数值。

表4列出了贝叶斯方法校准后SWCC模型的归一化常数的对数值和SWCC模型的备选概率。从表中可以得出，模型的备选概率从大到小依次为VGM>VGB>FX>VG。因此，新干莒洲岛库岸边坡红黏土最优的理论土水特征曲线是VGM模型，备选概率为38.3%。

对于每一个备选的SWCC模型，将每组参数对应的SWCC曲线进行排序，可得到SWCC模型估计的不同分位值，并依次计算得到SWCC模型估计的97.25%和2.5%分位值，以此绘制得到95%置信区间，如图6所示。图6中拟合曲线所使用的模型参数为后验分布中的最大似然值。从图中可以看出，备选概率越高的模型，95%置信区间能包络住的试验数据点就越多，证明了备选概率的有效性。

3 莒洲岛库岸边坡可靠度分析

江西赣江新干航电枢纽地处赣江中下游峡江水利枢纽的下一梯级。边坡区域内的露出地层以震旦系浅变质岩和第三系红层及第四系松散覆盖层分布最广。坡体中的岩石主要包括隔水岩层和相对隔水岩层。未经加固处理的莒洲岛库岸边坡地质剖面图如图7所示。在先前的确定性分析中，仅考虑降雨工况（即持续5 d且降雨量为100 mm/d的特大暴雨），其安全系数为0.719，若不采取护坡的加固措施，边坡将存在极大的失稳风险。

3.1 非饱和土边坡稳定性的数值分析

数值计算采用的模型为经过一次修坡加固后的新边坡。在边坡的数值计算模型中，潜在的滑坡体共划分为278个单元，单元最大边长尺寸为0.3～1 m的矩形或三角形。有限元网格对安全系数的影响在2.6%以内。滑坡体的岩土参数主要通过前期工程勘察资料、室内土工试验确定，边坡确定性分析的关键岩土参数和水力参数取值如表5所示。

边坡模型前缘常年被水淹没，因此，将边界条件设置为降雨边界，并附加变化的水位边界（用蓝色线段和粉色线段表示），其取值根据库区水位波动和日降雨量确定，边坡的后缘保持34 m的恒定水头边界，边坡底部设置为不透水边界。在滑坡体内设置变形监测点，观察边坡稳定性计算时的孔隙水压力变化和水头变化。数值计算模型如图8所示。

在Geostudio的渗流分析中，首先使用稳态分析进行初始渗流场计算，再利用Geostudio中的瞬态分析展复杂工况下边坡渗流状态的模拟。

图9为2021年新干水位站的水文信息，为了评估不同工况下莒洲岛边坡的稳定性，采用确定性分析展开3种较为极端的工况进行模拟：仅考虑水位升降的工况，库水位以2.2 m/d的速率保持5 d从27 m上升至38 m，然后保持5 d水位不变，最后以2.2 m/d的速率保持5 d从38 m下降至27 m；仅考虑降雨的工况，在保持初始状态后的第10 d开始为期5 d的100 mm/d特大暴雨；考虑水位升降和降雨的联合工况，即同时考虑上述的两种独立工况。

根据室内试验得到的莒洲岛库岸边坡红黏土先验数据，进行SWCC的参数校准和模型的适用性比较。VGM模型的备选概率为38.3%，因此，不考虑岩土参数空间变异性的边坡稳定性分析采用最为适用的VGM模型，分析结果的安全系数变化如图10所示。刚开始时，随着水位的骤然上升，由于存在指向滑坡体内的动水压力，边坡的安全系数呈现增大趋势，由初始的2.16增大至3.64。当库区水位保持38 m的最高位时，安全系数保持在3.56。当第10 d泄洪时，水位开始陡降并伴随着特大暴雨的到来，边坡的安全系数快速降低至1.11。结果表明，聯合工况对边坡的稳定性有着显著影响。

3.2 SWCC模型综合性的边坡稳定性分析

莒洲岛库岸边坡滑坡体的有限元数值计算模型共计278个单元，为了充分描述水力参数的空间变异性，单元尺寸不能大于第2变程的一半。因此将单元设为边长为0.3～1 m的矩形或三角形。变程表示随机场中变量的空间自相关范围，当空间中的两点距离小于变程时，距离越小相关性越强，距离大于变程时，则两点在空间上没有相关性。饱和渗透系数的均值，标准差。另外，随机场中的第1变程方向与坡面平行，坡面倾斜角为48°，第2变程的方向垂直于第1变程^[27]。设第1变程和第2变程均为5 m^[28]。初始变程比率=0.2。其他岩土参数如黏聚力、内摩擦角、弹性模量等按表5取值。根据不同SWCC模型参数的后验分布，分别进行10 000次抽样。采用36核CPU计算机使用抽样所得到的SWCC曲线对边坡进行稳定性分析，一次分析稳定在45 s左右，共36线程同时进行运算。将分析所得到的安全系数进行统计，并绘制出图11所示的边坡稳定性安全系数的PDF曲线。

当安全系数时，即为边坡失稳，每个SWCC模型对应的可靠度指标可根据公式（22）计算得到。 （22）

式中：为边坡的失效概率；为每个模型的抽样次数；为阶跃函数，用于判断边坡是否失稳；为逆函数。通过计算得到每个SWCC对应的可靠指标后，根据式（23）计算得到SWCC模型综合性的可靠度指标。 （23）

式中：为第j个SWCC模型的备选概率；表示SWCC模型数量为4个。根据《水利水电工程结构可靠性设计统一标准》（GB 50199—2013），边坡安全系数的可靠指标要求在2.70到4.27之间变化。图11是4个SWCC模型对应的边坡稳定性的可靠指标。

图12中的红色虚线表示考虑模型不确定性的可靠度分析结果的可靠指标=2.39。结果表明，如果考虑非饱和渗透系数的空间变异性，可靠度分析的结果不能满足规范中的要求（<2.70），且安全系数较低（均值在1.085～1.134之间波动）。与传统的确定性分析相比，其结果上要偏于危险，魏红卫等^[29-31]基于随机场理论探究了土体参数变异性对边坡稳定性的影响，也得出了类似的结论。因此，莒洲岛库岸边坡在遭遇2021年大暴雨和库区水位骤升陡降的复杂工况时，应采取护坡等的加固措施，如图13所示。

4 结论

基于土水特性试验和先验信息，通过贝叶斯方法量化理论模型的适用性，并校准对应的模型参数。考虑SWCC和非饱和渗透系数的空间分布特征，在暴雨和库区水位骤升陡降条件下，基于非饱和渗透系数随机场，利用GeoStudio2012软件开展莒洲岛库岸边坡稳定性的可靠度分析。得出以下主要结论：

1）针对莒洲岛库岸边坡红黏土，采用饱和盐溶液法和压力板仪法，得到了广吸力范围的压实土样的SWCC，并利用贝叶斯方法进行了SWCC模型的参数校准和模型比选，VGM模型的备选概率最高，即VGM模型是最适合于红黏土SWCC模型。

2）以赣江2021年5月底的极端降雨及水位骤升陡降为研究背景，开展莒洲岛库岸边坡稳定性的确定性分析。结果表明，降雨和水位变化对边坡稳定性的影响不是简单的叠加，两者的联合作用对边坡的稳定性影响要更为显著。

3）不同SWCC模型对应的莒洲岛库岸边坡的安全系数均值在1.085～1.134之间，可靠指标在1.34～2.96之间。这一结果表明，将非饱和渗透系数简化考虑为随机变量，考虑SWCC模型参数随机统计特征以及水力参数随机场，对边坡可靠度分析影响较为明显，相较于传统的确定性分析，其结果偏于危险。

参考文献

[1]  仉文岗， 王琦， 陈福勇， 等. 考虑岩体空间变异性的边坡可靠度分析及抗滑桩随机响应研究[J]. 岩土力学， 2021， 42（11）： 3157-3168.

ZHANG W G， WANG Q， CHEN F Y， et al. Reliability analysis of slope and random response of anti-sliding pile considering spatial variability of rock mass properties [J]. Rock and Soil Mechanics， 2021， 42（11）： 3157-3168. （in Chinese）

[2]  薛海斌， 党发宁， 尹小濤， 等. 非稳定渗流条件下非饱和土质边坡稳定性的矢量和分析法研究[J]. 岩土力学， 2016， 37（Sup1）： 49-56.

XUE H B， DANG F N， YIN X T， et al. A vector sum method for stability analysis unsaturated soil slope subjected to transient seepage [J]. Rock and Soil Mechanics， 2016， 37（Sup1）： 49-56. （in Chinese）

[3]  唐栋， 祁小辉， 蒋水华， 等. 不同前期降雨与土-水特征曲线对边坡稳定的影响[J]. 岩土工程学报， 2015， 37（Sup1）： 148-155.

TANG D， QI X H， JIANG S H， et al. Effect of different antecedent rainfalls and SWCCs on slope stability [J]. Chinese Journal of Geotechnical Engineering， 2015， 37（Sup1）： 148-155. （in Chinese）

[4]  王林， 李典庆， 曹子君， 等. 基于贝叶斯理论的土水特征曲线模型选择与参数识别方法[J]. 应用基础与工程科学学报， 2019， 27（6）： 1269-1284.

WANG L， LI D Q， CAO Z J， et al. Bayesian approaches for model selection and parameter identification of soil-water characteristic curve [J]. Journal of Basic Science and Engineering， 2019， 27（6）： 1269-1284. （in Chinese）

[5]  叶云雪， 徐帆， 刘小文， 等. 基于各向等压压缩和土的收缩试验预测脱湿路径下的土水特征曲线[J]. 岩土工程学报， 2023， 45（4）： 847-854.

YE Y X， XU F， LIU X W， et al. Prediction of soil-water characteristic curves under drying path based on isotropic compression and soil shrinkage tests [J]. Chinese Journal of Geotechnical Engineering 2023， 45（4）： 847-854. （in Chinese）

[6]  PENG L， CHEN B M. Fractal-based models study of the relative hydraulic conductivity and SWCC of bentonite by synchrotron radiation SAXS and X-ray computed tomography [J]. Fractals， 2021， 29（7）： 2150208.

[7]  潘振辉， 李萍， 肖涛. 黄土水分入渗规律的数值模拟研究[J]. 西北大学学报（自然科学版）， 2021， 51（3）： 470-484.

PAN Z H， LI P， XIAO T. The law of water infiltration in loess based on numerical simulation [J]. Journal of Northwest University （Natural Science Edition）， 2021， 51（3）： 470-484. （in Chinese）

[8]  丁小刚， 马丽娜， 蔺文博， 等. 非饱和重塑弱膨胀土孔隙结构与土-水特征曲线试验研究[J]. 岩石力学与工程学报， 2022， 41（Sup1）： 3081-3090.

DING X G， MA L N， LIN W B， et al. Experimental study on the pore structure and soil-water characteristic curve of unsaturated remolded weak expansive soil [J]. Chinese Journal of Rock Mechanics and Engineering， 2022， 41（Sup1）： 3081-3090. （in Chinese）

[9]  HUANG M S， JIA C Q. Strength reduction FEM in stability analysis of soil slopes subjected to transient unsaturated seepage [J]. Computers and Geotechnics， 2009， 36（1/2）： 93-101.

[10]  金磊， 曾亚武， 程涛， 等. 基于格子Boltzmann方法的土石混合体的渗流特性研究[J]. 岩土工程学报， 2022， 44（4）： 669-677.

JIN L， ZENG Y W， CHENG T， et al. Seepage characteristics of soil-rock mixture based on lattice Boltzmann method [J]. Chinese Journal of Geotechnical Engineering， 2022， 44（4）： 669-677. （in Chinese）

[11]  李梦姿， 蔡国庆， 李昊， 等. 考虑抗拉强度剪斷的非饱和土无限边坡稳定性分析[J]. 岩土工程学报， 2020， 42（4）： 705-713.

LI M Z， CAI G Q， LI H， et al. Stability of infinite unsaturated soil slopes with tensile strength cut-off [J]. Chinese Journal of Geotechnical Engineering， 2020， 42（4）： 705-713. （in Chinese）

[12]  蒋水华， 刘贤， 黄发明， 等. 考虑多参数空间变异性的降雨入渗边坡失稳机理及可靠度分析[J]. 岩土工程学报， 2020， 42（5）： 900-907.

JIANG S H， LIU X， HUANG F M， et al. Failure mechanism and reliability analysis of soil slopes under rainfall infiltration considering spatial variability of multiple soil parameters [J]. Chinese Journal of Geotechnical Engineering， 2020， 42（5）： 900-907. （in Chinese）

[13]  王长虹， 朱合华， 徐子川， 等. 考虑岩土参数空间变异性的盾构隧道地表沉降分析[J]. 岩土工程学报， 2018， 40（2）： 270-277.

WANG C H， ZHU H H， XU Z C， et al. Ground surface settlement of shield tunnels considering spatial variability of multiple geotechnical parameters [J]. Chinese Journal of Geotechnical Engineering， 2018， 40（2）： 270-277. （in Chinese）

[14]  RICHARDS L A. Capillary conduction of liquids through porous mediums [J]. Physics， 1931， 1（5）： 318-333.

[15]  HUANG M L， SUN D A， WANG C H， et al. Reliability analysis of unsaturated soil slope stability using spatial random field-based Bayesian method [J]. Landslides， 2021， 18（3）： 1177-1189.

[16]  CHEN Z Y， MORGENSTERN N. Extensions to the generalized method of slices for stability analysis [J]. Canadian Geotechnical Journal， 1983， 20（1）： 104-119.

[17]  宗振邦， 王長虹， 孙德安. 随机场-贝叶斯方法应用于非饱和土边坡稳定性可靠度分析[J]. 自然灾害学报， 2021， 30（2）： 127-137.

ZONG Z B， WANG C H， SUN D A. Application of random field-Bayesian method in stability reliability analysis of unsaturated soil slope [J]. Journal of Natural Disasters， 2021， 30（2）： 127-137. （in Chinese）

[18]  BECK J L， TAFLANIDIS A. Prior and posterior robust stochastic predictions for dynamical systems using probability logic [J]. International Journal for Uncertainty Quantification， 2013， 3（4）： 271-288.

[19]  MUALEM Y. A new model for predicting the hydraulic conductivity of unsaturated porous media [J]. Water Resources Research， 1976， 12（3）： 513-522.

[20]  BURDINE N T. Relative permeability calculations from pore size distribution data [J]. Journal of Petroleum Technology， 1953， 5（3）： 71-78.

[21]  VAN GENUCHTEN T H. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils [J]. Soil Sciences， 1980， 44（5）： 892-898.

[22]  FREDLUND D G， XING A. Equation for the soil-water characteristic curve [J]. Canadian Geotechnical Journal， 1994， 31（4）： 521-532.

[23]  高游， 孙德安. 单峰和双峰土水特征曲线基本参数的确定[J]. 岩土工程学报， 2017， 39（10）： 1884-1891.

GAO Y， SUN D A. Determination of basic parameters of unimodal and bimodal soil water characteristic curves [J]. Chinese Journal of Geotechnical Engineering， 2017， 39（10）： 1884-1891. （in Chinese）

[24]  潘登丽， 倪万魁， 苑康泽， 等. 基于VG模型确定土水特征曲线基本参数[J]. 工程地质学报， 2020， 28（1）： 69-76.

PAN D L， NI W K， YUAN K Z， et al. Determination of soil-water characteristic curve variables based on VG model [J]. Journal of Engineering Geology， 2020， 28（1）： 69-76. （in Chinese）

[25]  HSEIN JUANG C， LUO Z， ATAMTURKTUR S， et al. Bayesian updating of soil parameters for braced excavations using field observations [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2013， 139（3）： 395-406.

[26]  左自波， 张璐璐， 程演， 等. 基于MCMC法的非饱和土渗流参数随机反分析[J]. 岩土力学， 2013， 34（8）： 2393-2400.

ZUO Z B， ZHANG L L， CHENG Y， et al. Probabilistic back analysis of unsaturated soil seepage parameters based on Markov chain Monte Carlo method [J]. Rock and Soil Mechanics， 2013， 34（8）： 2393-2400. （in Chinese）

[27]  JIAN W X， XU Q， YANG H F， et al. Mechanism and failure process of Qianjiangping landslide in the Three Gorges Reservoir， China [J]. Environmental Earth Sciences， 2014， 72（8）： 2999-3013.

[28]  SUCHOMEL R， MA?IN D. Comparison of different probabilistic methods for predicting stability of a slope in spatially variablec-Φ[J]. Computers and Geotechnics， 2010， 37（1/2）： 132-140.

[29]  魏紅卫， 赵凡. 饱和渗透系数变异性对边坡破坏概率的影响[J]. 华南理工大学学报（自然科学版）， 2021， 49（8）： 95-102.

WEI H W， ZHAO F. Influence of saturated permeability coefficient variation on failure probability of slope [J]. Journal of South China University of Technology （Natural Science Edition）， 2021， 49（8）： 95-102. （in Chinese）

[30]  夏侯云山， 张抒， 唐辉明， 等. 考虑参数空间变异结构的结构化交叉约束随机场模拟方法研究[J]. 岩土力学， 2019， 40（12）： 4935-4945， 4962.

XIAHOU Y S， ZHANG S， TANG H M， et al. Study of structural cross-constraint random field simulation method considering spatial variation structure of parameters [J]. Rock and Soil Mechanics， 2019， 40（12）： 4935-4945， 4962. （in Chinese）

[31]  蒋水华， 刘贤， 黄劲松， 等. 考虑水力模型参数空间变异性土石坝边坡可靠度分析[J]. 应用基础与工程科学学报， 2021， 29（4）： 939-951.

JIANG S H， LIU X， HUANG J S， et al. Reliability analysis of slope stability of embankment dams considering spatial variability of hydraulic model parameters [J]. Journal of Basic Science and Engineering， 2021， 29（4）： 939-951. （in Chinese）

（编辑  胡玲）