基于云计算的电子信息技术在大数据处理与分析中的应用
高 阳
(单县教育和体育局,山东 菏泽 274300)
0 引 言
现如今,电子信息共享技术日趋便捷,大数据处理平台上的数据量也在持续增长,因此需要对相关大数据进行筛选处理和挖掘分析,以确保后续的数据分析和应用质量。但针对目前的传统算法应用来看,普遍存在查询完整性和精度不高、处理分析精度低等缺点[1]。
云服务器是大数据技术的硬件支持,为电子信息技术融合提供了客观条件。但是,以往的云计算在数据处理中存在硬件资源占用高的问题,而改进云计算方法能有效提升信息化建设水平。文章针对上述问题进行深入探讨,并基于云计算技术,形成大数据处理分析和挖掘的聚合算法模型[2]。
1 相关概念分析
1.1 基于云计算的大数据采集技术
云计算实施的前提是对采集数据的预处理,而标准化处理指标体系是预处理的保障机制,能够通过标准值进行采集数据的删减、补充。在标准化处理过程中,依据指标体系完成实际采集值和标准值的对比,以获取采集值的权重[3]。在大数据采集过程中,数据采集量与采集模型Wtr中的指标数量呈正相关,大数据采集模型为
式中:Ni表示评价指标体系中的指标值;Nm表示标准值。利用算术平均法获得指标综合评价的指数Vi,即
式中:Nt表示评价指标体系中的评价系数;Yi表示评级指标体系中设置的评价指标权数;Di表示第i类大数据采集指标值。基于上述模型建构分析,精准推进大数据采集工作[4]。
1.2 基于改进算法的大数据处理与分析
数据处理分析算法中,随机森林表现出色。然而,该方法在处理分析的流程中可能存在过度模仿的情况,增加数据的错误率,降低处理分析的准确率。为解决该问题,文章构建代价敏感学习函数R(A),以便将错误数据Ai的出现率降至最低。R(A)的计算公式为
式中:Mc表示的是在未分离情况下错误处理分析的成本;Mc(Ai)表示错误数据Ai的特征值。Mc(Ai)具有i个不同的值,分裂后会产生i个不同的分裂节点[5]。本研究需要计算每个子节点带来的错误处理分析值,由此测算最终分裂后的代价,Mc(Ai)的计算公式为
式中:n表示分裂节点数;ni表示第i个分裂处的节点数;pi表示第i个分裂处出现特性值的概率;FP表示错误分析的复杂程度;FN表示误处理分析指数。由于引入了代价敏感性,所建立的代价函数无法处理相关的数据。首先,计算多数类c1、少数类c0、数据集N的中心[6]。为实现对大数据的简化处理,文章提出改进代价函数。聚类中心的权重为IG(xk,ci),相关计算公式为
式中:xk表示第k个样本数据的特征值;ci表示第i个类型数据;p(x,c)表示在类型c中x出现的概率;p(x)表示数据集N中x的出现比率;p(c)表示数据集N中c的出现比率。
最终可知,聚类过程函数Hc(x)的计算公式为
式中:argmin(·)表示最小输出函数;αk表示第k个样本数据的差异系数;F[hk(x)]表示改进算法的大数据处理分析测算值[7]。
1.3 计算过程
在Map Reduce 模型里,本研究采用Canopy 与K-means 两种聚类算法,通过并行化的方式集成已经被划分的数据,从而完成数据处理、分析以及探索。基于云计算的大数据处理分析挖掘算法的实施步骤如下。
步骤1:数据集的划分阶段。假设利用改进随机森林处理分析后的数据集用[x1,x0,…,xn]表示,对其进行随机分片处理,处理结果用[splitl,split2,…,splitn]表示,将所有分片处理结果转换为
步骤2:Map 计算阶段。在转换后的数据分割结果中,本研究随机挑选了k个数据点作为初始聚类的核心。然后,利用欧氏距离来估算其他数据点与核心数据点的距离。其目的是为了进行数据类别的初步划分。在完成上述数据点的类别划分后,会生成
步骤3:融合阶段。依据Map 函数的输出数据,进行数据融合和分析,融合结果用
步骤4:Reduce 操作阶段。读取
2 实验结果分析
本研究收集的数据均进行标准化处理,且处理过程均在Hadoop 云平台上执行。其中,实验数据从数据集Amazon_initial、20-Newgroups、waveform 以及Covtype 中获取,并在此基础上对其展开电子信息数据映射分析,最终得到处理后的试验样本。为验证文章提出方法的有效性,与Canopy 算法和K-means 算法进行对比,指标包括查全率、查准率以及准确率。其中,查全率、查准率如表1 所示。

表1 查全率及查准率的对比分析 单位:%
由表1 可知,Canopy 算法的全查率和准查率最高值分别为86.5%和90.3%,最低值是72.1%、79.8%,平均值为79.89% 和84.09%;K-means 算法的查全率和查准率最高值是78.5%和86.1%,最低值是70.3%和73.7%,平均值分别是74.03%和80.45%;聚合算法的查全率和查准率最高值是98.7%和98.7%,最低值是95.6% 和94.1%,平均值是97.25%和95.76%。这表明文章所提算法的查全率和查准率最优。为进一步验证该算法的有效性,对比不同算法的准确率,如表2 所示。
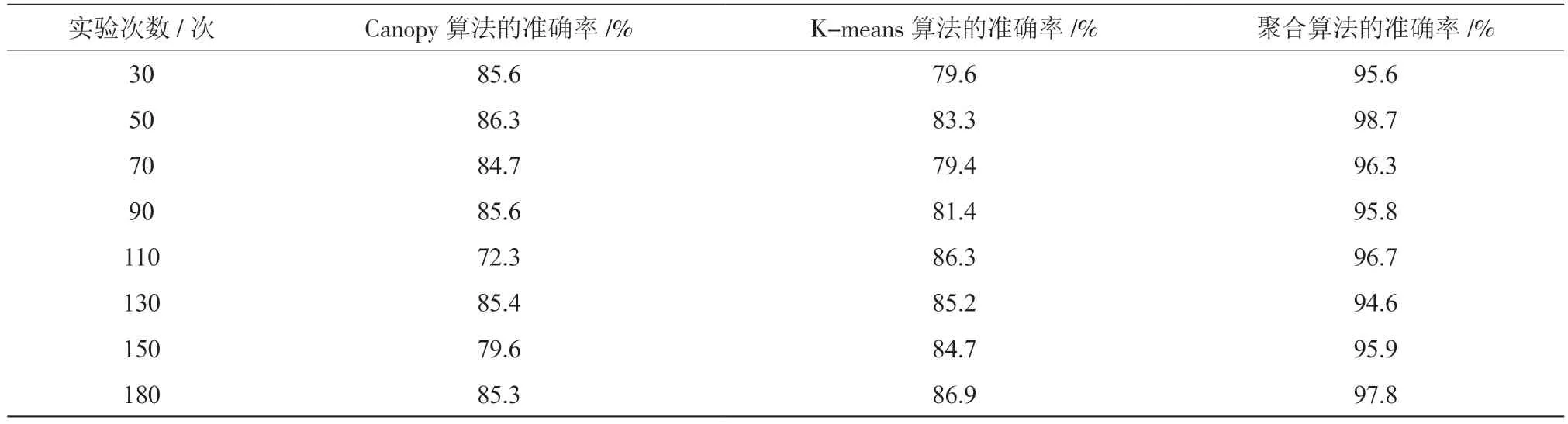
表2 基于云计算的大数据处理分析的对比结果
由表2 可知,在大数据处理准确率方面,Canopy算法的准确率最高值为86.3%,K-means 算法的准确率最高值为86.9%,而聚合算法的准确率最高值为98.7%,比Canopy 算法准确率最高值高12.4%,比K-means 算法准确率最高值高11.8%;Canopy 算法的处理准确率最低值为72.3%,K-means 算法的准确率最低值为79.4%,而聚合算法的准确率最低值为94.6%,比Canopy 算法准确率最低值高22.3%,比K-means 算法准确率最低值高15.2%。对3 种算法处理准确率的平均值进行评估,结果显示:Canopy 算法的平均准确率为83.1%,K-means 算法的平均准确率为83.4%,聚合算法的平均准确度为96.4%,分别比Canopy 算法和K-means 算法高13.3%和13.0%。
总体来说,上述模型中大数据计算的准确率基本保持在较高的水平,表明所用处理分析方式具有较强的精确度,能够有效实现对海量数据的准确处理分析。
3 结 论
综合上述研究表明,文章提出的聚合算法的平均准确率高于Canopy 算法和K-means 算法,应用效果较好。经过案例分析可知,聚合算法可以有效提高数据处理的准确率、查全率以及查准率,并确保海量数据的有效处理,提高云计算在电子信息技术领域的应用效果。

