基于PSO-SVM的Φ-OTDR系统模式识别研究

朱宗玖, 王宁

(安徽理工大学电气与信息工程学院, 淮南 232001)

相位敏感光时域反射仪具有分布式测量、抗干扰能力强、灵敏度高等优点[1-2],被广泛应用于能源输送管道安全预警[3]、输电线状态监测[4]、工程结构安全监测[5]、周界安防[6]等领域。然而,在实际的相位敏感光时域反射仪(phase sensitive optical time domain reflectometer, Φ-OTDR)系统中,传感光纤所处的环境复杂多变,天气变化、动物活动及行人误碰等因素的影响而产生的干扰可能会引起假报警,从而导致系统具有较高的误报率[7]。目前有两种方法用于降低Φ-OTDR系统的误报率,一是改进硬件结构,如采用Φ-OTDR与马赫-曾德尔干涉仪或迈克尔逊干涉仪相结合的方式,但该方法成本高且硬件结构复杂[8]。二是选优化模式识别算法,提高振动事件识别的准确率,进而降低系统误报率[9]。

为了在降低Φ-OTDR系统误报率的同时避免增加系统成本和复杂性,通常采用第二种方法。Wang等[10]提出了一种基于深度双路径网络的模式识别方法,对铁路周边的7种扰动事件进行分类,准确率达到97%,但更深的网络结构导致振动信号分类时间变得更长。Saleh等[11]采用变分模态分解(variational mode decomposition,VMD)和线性支持向量机(linear support vector machine,LSVM)对扰动信号进行分类,在信噪比为-4～-8 dB和-8～-16 dB的情况下分类精度分别达到79.5%和75.2%,识别的准确率较低。Zhou等[12]提出了一种YOLO(you only look once)与光纤振动传感系统相结合的方法对振动信号进行分类,但该方法只能识别单一类型的事件。

为了降低Φ-OTDR系统的误报率,缩短振动事件识别时间,提出一种多域特征提取与PSO-SVM相结合的模式识别算法。在特征提取阶段,对振动信号进行差分处理后通过小波包分解得到信号的能量特征,并与差分信号的时域特征相结合构成特征向量。在信号分类阶段,利用粒子群算法优化SVM分类器参数,并借助Ф-OTDR事件数据集进行验证。该方法突破了单一特征参量目标识别易受到干扰的问题,提高了多种扰动事件识别的准确性。

1 系统结构与原理

Φ-OTDR系统通过检测传感光纤中后向瑞利散射光的相位变化获取外界扰动信息[13]。传感光纤不受外界扰动影响时,系统产生的后向瑞利散射光相位近似保持稳定;当外界扰动作用在传感光纤上的某一段时,该位置后向瑞利散射光的相位发生相应变化,且变化幅度与扰动事件种类相关,通过对后向瑞利散射光强度进行解调,即可得到扰动信息。

在Φ-OTDR系统中,函数发生器(function generator,FG)产生脉冲,激光器发出的连续光经声光调制器(atoracousto-optical modulators,AOM)后转换为光脉冲信号,该光脉冲信号被输入到掺铒光纤放大器(erbium-doped fiber amplifier,EDFA)以提高输入功率,然后经环行器进入到传感光纤中,产生的瑞利散射光通过环行器反射回光电探测器(photoelectric detector,PD),接收到的信号由数据采集卡(data acquisition card,DAQ)采集,最后将数字信号存储在计算机上以用于后续分析。Φ-OTDR系统结构如图1所示。

图1 Φ-OTDR系统结构Fig.1 Φ-OTDR system structure

2 基于PSO-SVM的模式识别算法

2.1 光纤振动信号的特征提取

当Φ-OTDR系统受到外界扰动事件影响时,光纤振动信号的某些特征会发生相应变化,利用这些特征可以有效识别扰动事件种类。特征量较少会导致系统鲁棒性差、误报率高,因此采用多域特征提取来提高系统对扰动事件识别的准确率,增强系统的稳定性。

2.1.1 时域特征提取

时域特征值是衡量信号特征的重要指标。根据光纤振动信号时域波形中隐含的信息,如最大值、峰峰值、方差等,可以对扰动事件的种类进行识别。在提取光纤振动信号的时域特征时,为了消除数据本身的影响,首先对数据进行差分处理,然后再进行特征提取。从时域差分信号中提取的15个时域特征分别为:最大值、最小值、峰峰值、均值、方差、整流平均值、标准差、方根幅值、均方根、峰值因子、波形因子、峭度因子、脉冲因子、裕度因子、偏度因子。

2.1.2 小波包能量特征提取

光纤振动信号的统计特性随时间变化,即为非平稳信号。小波变换保留了傅里叶变换对信号频率的分析,同时又引入了时间分辨率的概念,对于复杂多变的非平稳信号,可以进行有效特征提取[14]。由于其固有性质,小波变换主要是对信号的低频成分进行处理,而对于光纤振动信号,需同时知晓它的低频与高频信息,以便全面的获取信号信息。小波包变换解弥补了小波变换对光纤振动信号高频部分分解的不足,可以对信号的全频分量进行分解,避免了信号特征的缺失。小波包分解原理如图2所示。

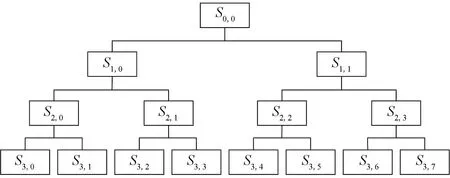
图2 小波包分解原理图Fig.2 Principle diagram of wavelet packet decomposition

通过小波变换对信号S0,0做N层分解,则信号S0,0可表示为

S0,0=SN,0+SN,1+…+SN,2N-1

(1)

式(1)中:SN,0,SN,1,…,SN,2N-1为信号S0,0经N层小波包分解后的子频带,则有

(2)

式(2)中:t为时间;i=0,1,…,2N-1;EN,i为子频带SN,i的能量。

由此提取光纤振动信号的小波包能量作为特征值,并结合时域特征组成特征向量。

2.2 光纤振动信号的识别

2.2.1 支持向量机

支持向量机(SVM)是一种从统计学习理论中衍生出来的二分类算法,已被广泛应用于模式识别[15-16]。其基本原理是对于非线性可分的数据,通过非线性映射函数转换到高维空间实现分类。

假设光纤振动信号的数据集T={(x1,y1),(x2,y2),…(xn,yn)},yi∈{-1,1},其中,i=1,2,…,n;xi为振动信号的特征向量集合;yi为振动信号种类的标签,其分类超平面可表示为

f(x)=ωTx+b

(3)

式(3)中:ω为权系数向量;x为样本空间内任意一点;b为偏置。

在SVM分类器中引入松弛变量ξi≥0,以容忍异常数据, 此时超平面求解问题变为约束条件下的凸函数优化问题,可表示为

(4)

式(4)中:c为惩罚系数,用于控制不满足最小区间的数据样本的贡献,当样本分类错误时,c越大,代表惩罚程度越重。

采用拟采用高斯核函数将x映射到高维空间φ(x)上,使样本空间线性可分,其中φ为映射函数。高斯核函数k(xi,xj)的表达式为

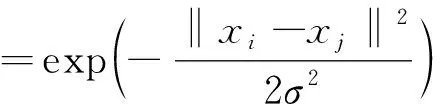
(5)

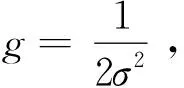
因此,可通过对参数c和g进行优化以提高SVM分类器的分类精度。

2.2.2 粒子群算法

粒子群算法(particle swarm optimization,PSO)是一种能够在全局范围内进行参数寻优的群体智能优化算法[17-18]。PSO算法将待优化问题的每种解转化为D维空间中包含N个粒子的粒子群,在每次迭代期间,粒子的速度和位置保持不变,在下一次迭代中,每个粒子根据当前个体最优位置与群体最优位置运动,最终获得最优解。粒子的速度和位置分别由式(6)、式(7)确定。

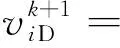
(6)

(7)

2.3 基于PSO-SVM的光纤振动信号识别步骤

惩罚因子c和核函数参数g对SVM分类器的性能起着决定性的作用,利用粒子群算法对SVM的参数c和g的选择进行优化。

基于PSO-SVM的光纤振动信号识别流程如图3所示。该算法的主要步骤如下。

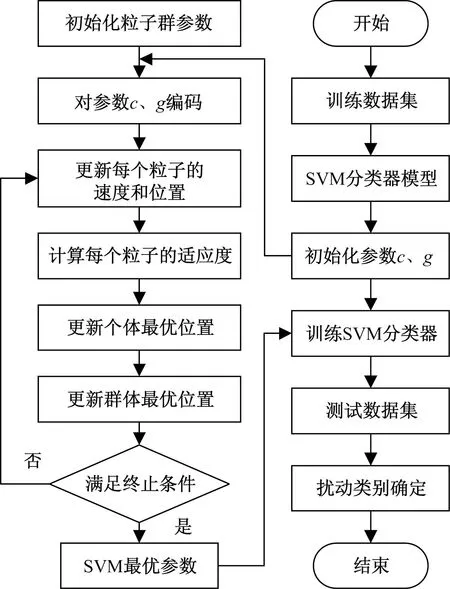
图3 光纤振动信号识别流程图Fig.3 Optical fiber vibration signal recognition flow chart

步骤1数据预处理。提取光纤振动信号的时域特征和小波包能量特征,并对特征向量进行归一化处理。

步骤2SVM分类器模型构建。选择高斯核函数作为SVM分类器的核函数,初始化惩罚因子c和核函数参数g。

步骤3参数优化。初始化粒子群后对参数c和g编码,利用数据集对c和g的选择进行优化,构建最优SVM分类器模型。

步骤4振动事件识别。利用优化后的SVM分类器对光纤振动信号进行识别。

3 实验结果分析

3.1 实验数据集介绍

为了验证本文算法的有效性,利用北京交通大学Ф-OTDR事件数据集[19]进行研究,该数据集包含背景噪声、挖掘、敲击、浇水、摇晃和行走6类典型事件,每个事件的时空信号样本在时域上由10 000个点组成,在空域上由12个相邻的空间点组成。数据集中每种事件对应的样本数量如表1所示。

表1 6种事件对应的样本数量Table 1 Number of samples corresponding to the six events

对6种事件进行差分处理后的结果如图4所示。从图中可以看出,背景噪声在时域和空域中分布均匀且强度低;挖掘和敲击事件都有一个明显的峰值,由于泥沙的回流作用,挖掘事件具有较长的时间分布;浇水和摇晃事件在时域中都为连续信号;根据人走路的步频,行走事件在单个样本中具有多个不同的峰值。

3.2 多域特征提取

特征的类间距离与类内距离之比可以表征其识别能力,提取的特征要尽可能使不同模式的信号具有较大的类间距离,相同模式的信号特征具有较小的类内距离,且需要考虑减少数据量以方便后续运算。因此,在对振动信号进行时域特征提取时选择8个类间距离大、类内距离小的特征,分别为最大值、最小值、峰峰值、方差、整流平均值、均方根、峰值因子和裕度因子。根据8个特征的类间距离,从中随机选取20个样本第六空间采样点中区别较为明显的两个特征,如图5所示。

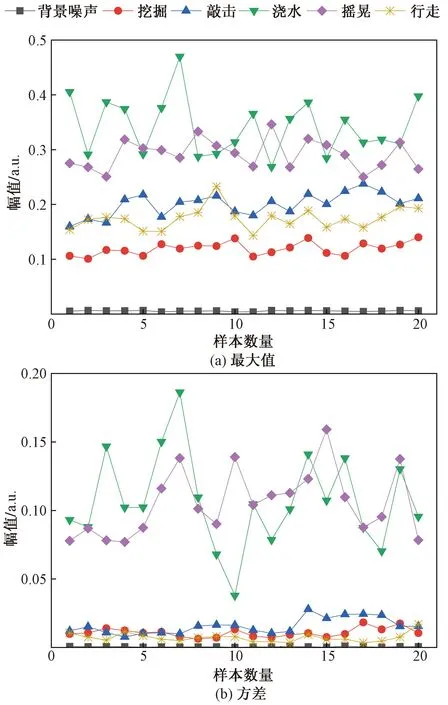
图5 6种扰动事件的两个时域特征Fig.5 Two time-domain characteristics of six disturbance events

光纤振动信号经过小波包分解成不同分布的子频段,随分解层数的增多,信号频带划分的越精细,提取到的信号信息越丰富,但分解信号所需时间将大大延长,且提取的特征向量维度将呈指数级增加,延长分类算法的计算时间,因此分解层数并不能越多越好。为了确定小波包分解的最佳层数,对数据集中的样本采用db3小波基进行不同层数的分解,与时域特征结合,组成相应分解层数的特征向量,使用PSO-SVM分类器观察平均分类准确率的变化,结果如图6所示。

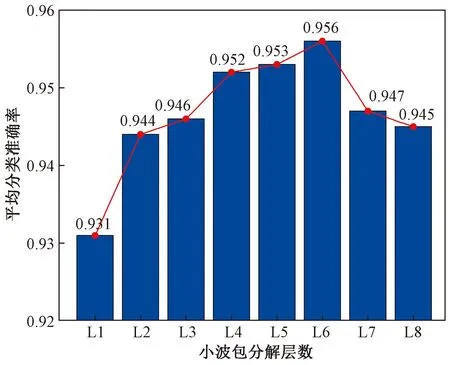
图6 不同小波包分解层数的平均分类准确率Fig.6 The average classification accuracy of different wavelet packet decomposition levels

从图6可以看出,分解层数低于6层时,平均分类准确率随分解层数的增加而增加,在分解层数为6时达到最大值,当分解层数大于6时,平均分类准确率呈下降趋势。在综合分类精度与计算时间的考虑下,选择6层小波包分解提取光纤振动信号的特征。

3.3 实验结果

由于不同特征的幅值数量级相差较大,为了防止幅值较小的特征在分类时失去作用,采用Max-Min归一化对特征向量x=(x1,x2,…,xn)进行处理。

(8)

式(8)中,x′i为归一化后的结果;xi为原始数据;xmax、xmin分别为所对应参数的最大值和最小值。

采用的数据集共包含15 612个样本,将其中的70%(10 928个样本)划分为训练样本,另外的30%(4 684个样本)划分为测试样本,采用提出的模式识别算法进行分类,将分类过程重复多次以获得平均结果,为了分析本文算法的分类性能,分别给出6种事件的混淆矩阵和入侵事件(包括挖掘、敲击、摇晃)与非入侵事件(包括背景噪声、浇水、行走)的混淆矩阵,分别如图7、图8所示。

混淆矩阵对角线上的值表示正确的分类结果

混淆矩阵对角线上的值表示正确的分类结果

从图7中可以看出,本文算法对6种事件分类的准确率均超过了90%,平均分类准确率达到95.6%,其中,挖掘、浇水和摇晃事件在识别时有一些偏差,4.0%的挖掘事件被识别为敲击事件,6.0%的浇水事件被识别为摇晃事件,5.3%的摇晃事件被识别为浇水事件,这与它们的时域特征相似有关。入侵事件识别的准确率达到96.9%,非入侵事件识别的准确率为96.4%。为了进一步分析分类器性能,表2给出6种事件的精确率、召回率和F1值。

表2 算法评价指标Table 2 Algorithm evaluation index

在样本数据一致和特征向量提取方法相同的情况下,使用SVM、GA-SVM等常用分类算法对6种事件进行识别,结果如表3所示。可以看出,SVM、GA-SVM的平均分类准确率分别为90.7%、93.6%,PSO-SVM的平均分类准确率最高,为95.6%,说明PSO-SVM能够更有效地识别光纤振动信号。

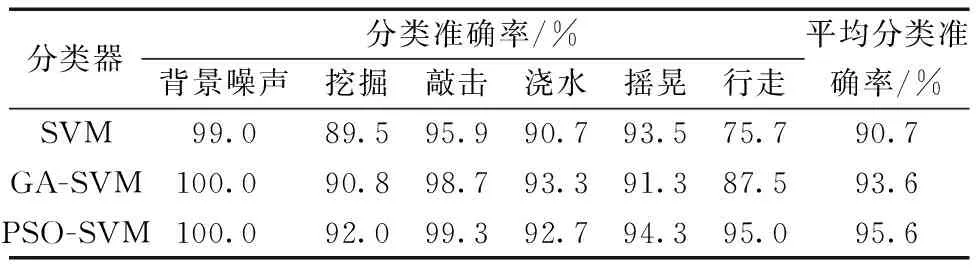
表3 不同分类算法的平均分类准确率Table 3 Average classification accuracy of different classification algorithms

4 结论

(1)针对Φ-OTDR系统中误报率高的问题,提出了一种多域特征提取与PSO-SVM算法相结合的模式识别方法。该方法突破了单一特征参量事件识别准确率低的问题,提高了系统的可靠性。

(2)通过对数据集中的样本进行不同层数的小波包分解以确定最优分解层数,提取相应分级层数的小波包能量后与时域特征相结合组成特征向量,并将其放入分类器中训练,对6种事件(背景噪声、挖掘、敲击、浇水、摇晃、行走)分类的准确率分别为100%、92.0%、99.3%、92.7%、94.3%、95.0%,平均分类准确率达到了95.6%。

(3)在样本数据一致和特征向量提取方法相同的情况下与SVM、GA-SVM进行对比,结果表明:所提出的模式识别方法能够较好地识别不同类型的扰动事件,可为Φ-OTDR系统性能的进一步提高提供有益参考。