基于滑模变结构的风电机组一次调频算法研究

李继超, 贾梦欣, 陈超波, 张彬彬*, 王坤, 杨冰

(1.西安工业大学电子信息工程学院, 西安 710021; 2.西安应用光学研究所, 西安 710065)

风力发电作为有潜力的新能源之一,因其发电密度高而污染较小,发展迅速[1]。为了解决大规模风电场参与并网时导致的系统惯量降低、调频能力不足等问题,相关并网准则要求风电场应具备一次调频能力[2]。然而由于风能的波动性、间歇性,以及电网的不稳定性,当风电场机组全功率参与一次调频时,采用经典控制算法可能会导致输出功率超调较大,甚至引起风电机组脱网,严重时还会造成大范围脱机事故,影响用电安全,因此,提高风电场一次调频能力,对于提升其并网安全性,具有重大的研究意义和工程价值[3]。

为了提高风电机组一次调频能力,避免风电机组脱网,学者们对风电机组一次调频控制方法展开大量研究[4]。传统一次调频控制利用虚拟惯量和下垂控制使机组参与调频,并采用比例积分微分(proportional integral differential,PID)削弱频率振荡。文献[5]利用虚拟惯量和下垂控制使双馈感应发电机(double fed induction generator,DFIG)参与电网一次调频,研究DFIG功率调度原理和频率响应过程,增强了DFIG响应频率变化时的有功和无功功率调节能力。但DFIG相较于永磁同步发电机(permanent-magnet synchronous motor,PMSM),并网时频率调节能力略有不足,且虚拟惯量和下垂控制鲁棒性较差,需要进一步改进。文献[6]以直驱型永磁风电机组为研究对象,在永磁风电机组保留备用功率的情况下,采用虚拟惯量与变桨控制相结合的方式使风电机组完成一次调频,但仅利用桨距角的变化提供频率支撑,在风速突变时难以维持系统稳定,不利于电网安全。文献[7]根据风电机组的数学模型,在Simulink平台上搭建了系统仿真模型,并在给定风速下对不同PID参数的变桨距控制系统进行仿真实验,结果验证了合适的PID参数能有效改善控制系统的动态特性,但PID控制本身存在易产生超调的特点,波动较明显。

针对PID控制的不稳定性,将滑模变结构引入一次调频控制。文献[8]提出了基于神经网络的风电机组变桨距滑模控制策略,以变桨距控制方法为主,利用模糊C均值聚类法与递推最小二乘法,将滑模误差引入到变桨距滑模控制自适应律中,利用MATLAB/Simulink分析了电压电流功率随风速波动产生的变化。但神经网络具有依赖人工经验的缺点,难以适用于实际中多变的情况。文献[9]利用滑模控制对研究对象模型误差、参数变化以及外部干扰不敏感的优点,在系统仿真时加入扰动,验证控制方案的有效性。但是未解决滑模变结构控制中抖振较多的问题。

以上控制方法均存在复杂性较高,抖振强的问题,针对风电机组一次调频系统多变量、非线性的特点,文献[10]提出一种sigmoid函数趋近率的滑模变结构控制算法。即在采用变速和变桨距的联合控制系统中,以系统频率偏差为状态量,建立滑模面,设置趋近率,分析稳定性,优化系统性能。由于滑模控制具有非线性、变结构、自寻优等特点,还能抑制风电机组系统的参数时变与非线性因素,因此非常适合风电机组一次调频这样的强耦合系统。

利用MATLAB/Simulink软件对风电机组一次调频过程进行仿真,模拟实际风力发电系统的工作状态,明确电网频率和风速变化对整体系统的影响,实现一次调频滑模控制,以验证控制策略的有效性、可行性,为今后制订进一步的功率分配方案、预防事故发生提供有效参考。

1 风力发电机组数学模型

风电机组控制系统主要由风力机、齿轮箱、发电机、背靠背型变流器及电网组成,如图1所示。风力机捕获风能并转化为机械能,齿轮箱将风力机转速升速,以达到发电机启动转速,发电机转化机械能为电能,经过背靠背型变流器滤波、变压器升压后,与电压源相连。

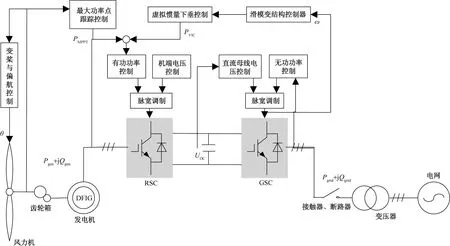
θ为风机桨距角;PMPPT为MPPT模式运行时风力机捕获的功率;PVIC为功率指令;ω为系统角频率;Pgen、Qgen分别为电机的有功功率和无功功率; RSC为机侧变流器;UDC为直流母线电压;GSC为网侧变流器;Pgrid为网侧输出有功功率;Qgrid为网侧输出无功功率

1.1 永磁同步风力发电机数学模型

PMSM具有发电效率高,原理结构简单,调速范围广等优点,是目前风电机组中发电机的主要机型。主要由定子、转子和端盖等部件组成,定子与常规感应电机基本相同。其中,电枢绕组可采用集中整距绕组,也可采用分布短距绕组与非常规绕组[11]。

dq坐标系中永磁同步发电机的数学模型如下。

定子电压方程为

(1)

磁链方程为

(2)

电磁转矩方程为

(3)

式中:uds、uqs、ids、iqs、φds、φqs分别为定子的电压、电流和磁链的dq轴分量;φm为永磁体产生的主磁链;ωr为转子角速度;p为微分算子;Lqs、Lds分别为定子的q轴和d轴的电感;np为发电机极对数;Rs为定子电阻。

1.2 最大风能捕获

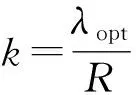
(4)

式(4)中:R为风轮半径;ρ为空气密度;kmax为最大风机功率系数;Vwind为风速;ωw为电机转速;P为风力机捕获的风能所对应的功率。

1.3 机侧电压电流矢量控制

机侧转子永磁体中心轴为d轴,根据电阻电感磁链及电压电流的耦合关系,在dq坐标系下,永磁同步电机的电压控制方程可表示为

(5)

式(5)中:rs为内阻;Ld、Lq为电感;φpm为相位裕量。

结合式(5),如果ids变化会引起iqs变化,那么相反的,iqs变化也会使ids变化,这不利于控制[13]。为实现ids和iqs的解耦控制,设计方程为

(6)

式(6)中:Kp1、Kp2为定子电流误差系数,通常取1;Ti1、Ti2为时间常数。

永磁同步风电机组电流解耦控制原理如图2所示。

u1d、u1q、i1d、i1q、e1d、e1q分别为定子电压,电流和电动势的dq轴分量;为电压和电流的d轴给定值;Pgen为电机有功 功率;为总的功率指令;PI和ωL为控制环节

1.4 网侧电压矢量控制

根据电网侧有功及无功功率控制方法,取电网电压电流方向与dq坐标系下的d轴方向一致,因为dq轴相差90°,所以电网电压电流在q轴上的矢量分量为0,因此有功无功功率与网侧电压电流关系为

(7)

式(7)中:egd、igd分别为电势和电流给定值在d轴上的分量。

假设网侧电压恒定,那么网侧有功功率Pg和无功功率Qg将直接是igd和igq的线性函数,仅有正负区别。

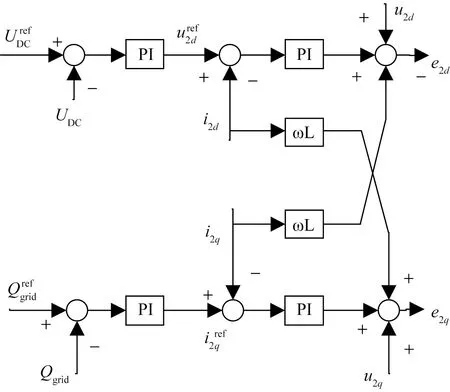
UDC为网侧直流电压值;为网侧无功功率给定值

1.5 一次调频滑模控制器设计

传统一次调频控制常由虚拟惯量控制和下垂控制联合实现[15]。虚拟惯量下垂控制的输入量为系统角频率ω,系统角频率由网侧锁相环得到。当系统频率发生突变,虚拟惯量与下垂控制器将频率变化转换为功率偏差,通过机侧变流器功率控制调节机侧功率指令ΔP,抑制频率变化,可表示为

(8)

式(8)中:kp为下垂控制系数;kd为虚拟惯性控制系数;Δω为系统角频率指令,Δω=ω-1。

但此一次调频方法效果不理想,频率谐振较多、有功功率输出波动明显,不利于电网稳定。因此,在原控制系统的基础上,引入滑模变结构控制。定义滑模控制器切换函数S为机侧功率指令ΔP与系统实际机侧输出功率Pg之差,即

S=ΔP-Pg

(9)

对式(9)进行求导,得切换函数导数为

(10)

将式(8)代入式(10)得

(11)

为了消除抖振,采用激活函数代替符号函数作为趋近率设计滑模控制器,增加边界光滑度,如图4所示。

图4 趋近率Fig.4 Approach rate

设

(12)

式(12)中:M为放大倍数;sgn(S)为激活函数,可表示为

(13)

由式(11)、式(12)可得

(14)

因为ω=2πf=Δω+1,其中f为系统频率,代入式(14)可得

(15)

由式(9)～式(15)可得一次调频滑模控制原理框图如图5所示。

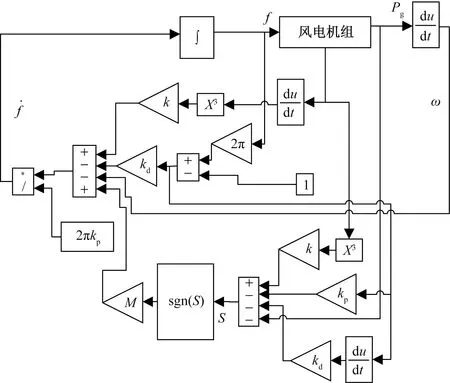
Pg为发电机输出有功功率;ω为系统角频率;kp、kd分别为虚拟 惯量系数和下垂系数;K为常数;M为激活函数放大倍数

1.6 稳定性分析

为了验证滑模变结构控制器的稳定性,选择李雅普诺夫函数V为

(16)

对李雅普诺夫函数求导,所要满足的稳定性条件为

(17)

式(17)中:ΔP为机侧功率偏差指令,分为大于零和小于零两种情况,当机组输出功率较小,ΔP为升功率指令,大于零且大于Pg,则S>0,又因为-Msgn(S)<0,则稳定性条件小于零;反之,ΔP为降功率指令,小于零,则S<0,又因为-Msgn(S)>0,则稳定性条件小于零。

综上所述,一次调频滑模控制器满足李雅普诺夫稳定性条件。

2 永磁同步风力发电机组整体仿真分析

2.1 系统仿真

为了验证滑模变结构控制策略的可行性,根据风电机组的数学模型,在MATLAB/Simulink中建立该系统的仿真模型,如图6所示。该系统主要由风力机模块、发电机模块、背靠背型变流器和电网组成。

风力机模块在风速、转子转速和桨距角的作用下,输出转矩提供给发电机,永磁同步发电机产生三相电压电流依次与变流器、输电线路、变压器和电网相连,变流器采用背靠背双PWM变流器。风力机模块中利用风速与转子转速实现桨距角控制。在机侧加入负载,实现各个部件的负载综合。仿真系统参数如表1[16]所示。

表1 风电机组参数[16]Table 1 Wind turbine parameters[16]

2.2 仿真结果与分析

令风速在0.5 s时由0增长到13 m/s,超过额定风速12 m/s。在经典控制模式下,风速变化直接影响转子转速变化,转子转速按照一定比例进行跟踪,保证一直在最佳叶尖速比,从而实现最大风能捕获。当风速过大使得电机转速超过额定转速时,桨距角增大,使风力机捕获的机械功率减小,有效限制电机转速在额定范围内。滑模变结构控制与经典控制方法相比,相应速度更快,误差范围更窄,稳定性更高。如图7所示,为风速、转子转速、桨距角变化曲线。

图7 风速、转子转速、风机桨距角曲线Fig.7 Curves of wind speed, rotor speed, fan pitch angle

电网频率骤降,机侧、网侧输出有功功率突增,经控制器调节后,随着电机转速的变化,在8 s后网侧电压趋于1 000 V,电流趋于2 000 A,有功功率在-2 MW附近;机侧电流趋于2 000 A,有功功率在2 MW附近。滑模控制器相较于经典控制方法,不仅消除了抖振与超调,还具有很强的抗干扰性,如图8所示。

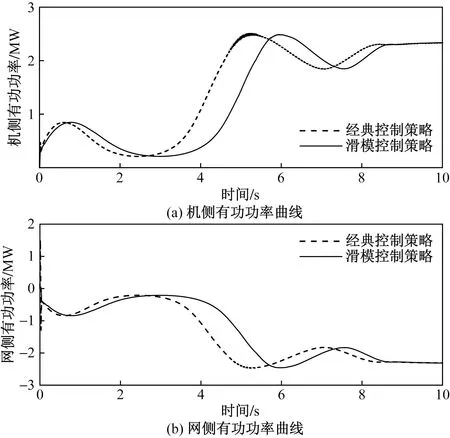
图8 机侧、网侧有功功率曲线Fig.8 Active power curves of machine side and network side

电网频率在0.05～0.06 s突降0.2 Hz,系统频率降低,出现频率偏差。一次调频控制使机组有功功率指令上调,有功功率输出突增,实现频率支撑。当频率偏差缩小时,机组有功功率指令下降,输出有功功率降低,频率恢复到50 Hz。如图9所示,滑模变结构控制器与经典控制策略相比,利用频率反馈值快速消除波动,缩小了振动范围,削弱了大多数抖振。

图9 系统频率曲线Fig.9 System frequency curve

永磁同步电机电磁转矩和机械转矩如图10所示,在0.05～0.06 s频率发生振荡后电磁转矩和机械转矩经滑模控制器立即调整,消除了超调,9 s后都稳定在-1×106N·m,且经控制器后也能够较好的跟踪转矩变化。

图10 电磁转矩和机械转矩曲线Fig.10 Electromagnetic torque and mechanical torque curves

背靠背型变流器对三相电压电流进行交直流变换,其中直流母线电压如图11所示,频率突降后,电压突增,经过PID控制,在0.2 s时稳定在1 200 V。滑模变结构与经典控制策略相比,速度更快,过度更光滑,且基本消除了超调,有利于电网稳定。

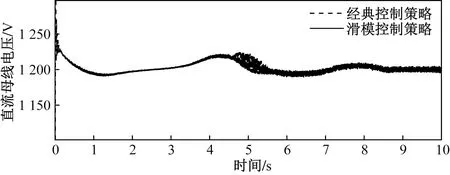
图11 直流母线电压曲线Fig.11 DC bus voltage curve

3 结论

为了得到抗干扰性强、不易发生脱机事故的风电机组一次调频系统,将滑模变结构引入一次调频控制环节,并在MATLAB/Simulink平台上建模仿真,验证控制策略的可行性。滑模变结构控制与经典PID控制策略相比,不仅对系统不确定因素具有较强的鲁棒性,而且可以通过滑模的设计获得满意的动态性能,仿真结果也验证了所提控制策略的有效性,使电网频率能够在系统扰动或者突变风速下振动较小的稳定在额定值内,提高了电网性能和风能利用率。

综上,对于风电机组动态模型的研究是风电并网的首要前提,将滑模变结构引入一次调频控制系统也是并网控制的新突破点,为分析PMSM风电机组并网后与电力系统之间的相互影响奠定了基础,为进一步制订风力发电相关政策和实施办法提供了理论支撑。