采用迁移学习的表面肌电信号手势识别方法

胡学政, 陶庆, 赵暮超, 刘景轩, 马金旭

(新疆大学机械工程学院, 乌鲁木齐 830017)

人机交互是人与计算机或智能体之间交流对话、互换信息、协作配合的桥梁,涉及对人与计算机或智能体之间接口的科学含义和实践的深入研究[1-2]。近年来,基于生物电信号的人机交互模式已经成为领域研究的热点内容[3-4]。相比于脑电信号空间分辨率低、采集烦琐等特点,表面肌电信号(surface electromyography,sEMG)的获取渠道简单且成熟,能够提供丰富的信息。此外,它的采集方式可以是无创采集,因此受到越来越多学者的青睐[5-6]。

基于sEMG进行意图识别已有许多成功案例,在上肢、下肢等领域都已得到广泛应用[7]。Wen等[8]采用最大互信息(MMI)对超参数(包括特征、窗口长度和状态数)进行优化来构建手部动作的隐马尔可夫模型(HMM),通过40个手部动作进行验证,获得了97%的准确率。Liu等[9]提出了一种新的对数-梅尔-频谱(log-MFS)特征,该特征可以减少力变化对肌电图模式识别(EMG-PR)方法分类性能的影响,增强基于EMG-PR的系统在实际应用中对抗力变化的鲁棒性, 对于未经训练的高、低力水平,平均分类准确率分别提高了约27%和11%。林恒等[10]提出了差分共空间模式(differential common spatial patterns,DCSP)特征,该特征在采用不同的分类器进行动作分类时具有较高的鲁棒性,不依赖分类器的选择。赵诗琪等[11]提出了一种FS(Fisher score)降维方法,通过FS与SVM结合进行手势识别,既提高了准确率又缩短了训练时间。采用传统机器学习方法进行手势识别所需数据量少,训练时间短,但是特征提取过程复杂烦琐,而且所提取的特征对于分类器来说可能并不是一个良好特征。

随着深度学习的崛起,越来越多学者开始采用深度学习进行手势识别研究[12]。Rahimian等[13]提出了一种基于混合识别模型(hybrid recognition model, HRM)和时间卷积网络模型(temporal convolutional network model, TCNM)的深度学习网络结构,以NinaPro DB2公用数据集进行测试,分别获得了98%和92%的准确率。Fang等[14]提出了一种与假手交互的手势和力的同时识别方法,变化力可以实现更精细的控制并缓解肌肉疲劳,截肢者手势的平均识别准确率为78%,力的平均识别准确率为76%。Cté-Allard等[15]采用迁移学习来处理多用户的聚合数据,同时利用深度学习从大型数据集中学习判别特征来进行手势识别。Lai等[16]提出了一个对比自监督学习框架(ConSSL)以实现目标域的域适应,实验结果表明虽然标记样本的数量相对较少(≤50%),但该框架仍然达到>90%的识别精度。相比传统机器学习,深度学习识别准确率高,但所需数据量庞大,训练时间较长。

采用表面肌电信号进行手势识别在客观情况下可以取得良好的效果,但面临电极贴片位移、受试者动作变化等情况,会使得用户间数据差异变大,识别准确率会有所下降。为解决上述问题,提出一种基于迁移学习的手势分类模型。通过流形嵌入分布对齐(manifold embedded distribution alignment,MEDA)方法[17]执行流形特征学习,解决迁移学习域适应中存在的特征退化问题,同时执行动态分布对齐以定量调整边缘分布和条件分布,减小不同受试者之间的数据差异。通过实验验证MEDA方法在复杂情况下的手势分类中具有良好的准确性与鲁棒性,解决了复杂情况下手势识别的准确率,为拟人化智能假手提供了理论依据。

1 实验设计与信号采集

1.1 实验设计

本次实验采用4种日常生活中常用的手势进行手势分类,分别是五指伸展、握拳、ok伸展以及大拇指伸展,如图1所示。信号采集范式采用E-Prime软件与计时器相结合的方法,如图2所示。

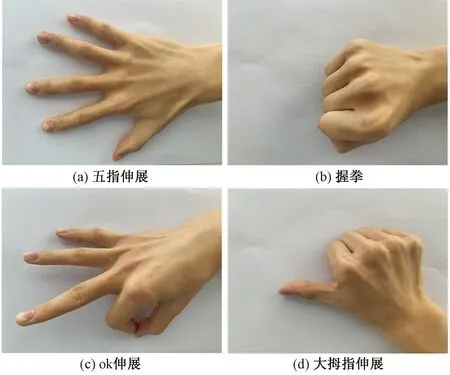
图1 4种生活中常用手势Fig.1 Four common gestures in life

图2 信号采集实验范式Fig.2 Signal acquisitionexperimental paradigm

实验开始前,先在采集区域用浓度为70%的酒精进行擦拭,以防止在采集过程中出现电极贴脱落的情况。受试者注视“+”3 s后实验开始,当屏幕上出现手势照片时进行为时1 s的手势动作,出现黑色背景时休息1 s,计时器以每1 s响应一次的频率加以辅助,每种动作以放松-动作-放松的形式采集20次。采集完一类手势动作后休息5 min再进行下一类手势动作的采集,以防止受试者肌肉疲劳。

1.2 表面肌电信号采集

选取葡萄牙PLUX公司生产的biosignalsplux Hybrid-8生物信号采集系统进行sEMG采集,采样频率为1 000 Hz。实验采用一次性表面电极贴片进行右臂四通道sEMG的采集,在实验开始前要用酒精擦拭受试者电极贴片处的肌肉。电极贴片位置如图3所示,4个采集点距离肘关节40～50 mm,各采集点围绕前臂等距分布,同一采集通道的两电极间隔20 mm,将接地电极放置于受试者的第7节颈椎。

1～4为采集点

来自新疆大学的11名健康受试者参加实验,受试者均无关节或上肢肌肉疾病史,共计男生9名,女生2名,均为右利手,平均年龄(23±1.5)岁(用均值±标准差表示)。11受试者都是自愿参加,且在进行实验前都已经签署了实验知情书。

1.3 数据预处理

sEMG的主要频率集中在20～300 Hz,在其采集过程中容易受到基线漂移以及50 Hz的工频干扰。首先采用四阶巴特沃斯带通滤波器消除基线漂移,滤波器的频率设置在20～300 Hz,在此基础上选取50 Hz陷波器消除工频干扰。由于sEMG的采集过程中存在休息区间,因此需要对采集到的数据进行活动段提取,图4展示了sEMG的活动段提取。采用滑动时间窗口进行活动段提取,时间窗口长度设为128,滑动窗口长度设为64。采取4个通道平均能量和最大值的0.06h倍作为阈值(h为经验取值),起止点采用多次阈值判断,即连续超过5次阈值判定活动段起止,在活动段前后采用数据补充防止丢失有效信息。

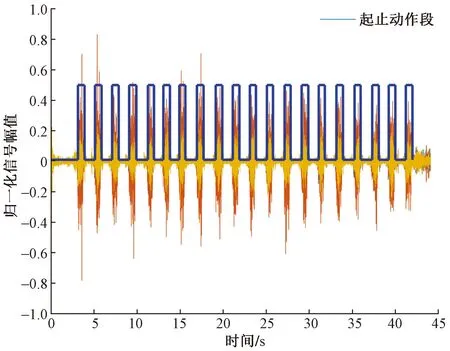
图4 sEMG活动段提取Fig.4 sEMG activity segment extraction

1.4 特征提取

良好的特征对于分类有着不可或缺的作用,能对不同的手势进行区分。采用具有重叠部分的滑动时间窗的方法进行特征提取,从采集到的4个通道的肌电信号中提取时域特征和频域特征并进行归一化处理。

提取绝对平均值、均方根值、方差、波形长度4个时域特征[18]。相关的计算公式如表1所示。

表1 时域特征计算公式Table 1 Calculation formula of time domain characteristics

选取平均功率频率、中值频率两个频域特征[19]。相关计算公式如表2所示。

表2 频域特征计算公式Table 2 Calculation formula of frequency domain characteristics

2 方法原理

MEDA方法首先执行流形学习与动态分布对齐,然后通过SRM原理进行总结来获得一个域不变分类器f,首先定义g(·)为流形特征的学习函数,然后给出域不变分类器f的定义为

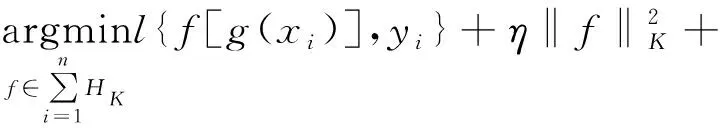
(1)

2.1 流形特征学习

格拉斯曼流形[20]用于解决由线性子空间组成的数据,选取测地线流核(geodesic flow kernel,GFK)[21]作为格拉斯曼的核函数。MEDA从格拉斯曼流形G中学习g(·),在执行流形特征学习时,使用d维子空间对数据进行建模,将源领域特征矩阵和目标领域特征矩阵嵌入称为G的集合中,G代表所有的d维子空间。每个d维子空间在G中对应一个点,通过测地线流Φ(t):0≤t≤1来绘制两个d维子空间之间的路径,其次t为两个域之间的距离。把源领域特征矩阵的子空间表示为Φ(0),目标领域特征矩阵的子空间表示为Φ(1),找到一条Φ(0)～Φ(1)的测地线流,相当于将原始特征转换为无限维特征空间,最终消除源领域和目标领域的数据差异。

2.2 动态对齐分布

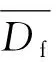
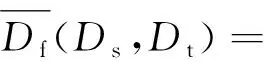
(2)

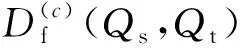
使用最大均值差异(maximum mean discrepancy,MMD)来计算域之间的分布差异,采用投影MMD[22]来计算与分类器f相关的MMD,此时两域间的动态分布对齐定义为

(3)

式(3)中:E[·]为嵌入数据的平均值;zs为源域数据;zt为目标域数据。

目标领域中没有标签,条件分布Qt=Qt(yt|zt)无法直接计算得到,采用类条件分布Qt=Qt(zt|yt)来近似Qt。使用在Ds上训练的基本分类器的预测结果应用于Dt,以获得Dt的软标签。由于软标签的可信度较低,因此通过迭代来进行优化,首次迭代时采用原始分类器,后续迭代过程中MEDA会根据上一次的迭代结果对Dt的标签进行优化。

将μ视为一个参数,其最终取值采用交叉验证来获取。由于目标领域没有标签,所以通过利用域的全局和局部结构来计算μ。采用A距离作为基本测量,A距离被定义为建立线性分类器来区分两个域的误差。将ε(h)为线性分类器h区分源领域和目标领域和的误差。A距离可定义为

dA(Ds,Dt)=2[1-2ε(h)]

(4)

(5)

2.3 域不变分类器

经过流形特征学习和动态分布对齐以后,通过总结SRM原理总结以上两个步骤来学f,给定最终域不变分类器f的数学定义为

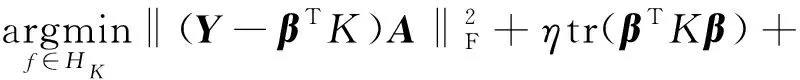
(6)

式(6)中:β为系数向量;K为核函数;‖·‖F为弗罗贝尼乌斯范数;A为对角域指示矩阵;Y为源领域和目标领域的标签矩阵;tr(·)为跟踪操作;M为MMD矩阵;L为拉普拉斯矩阵。

2.4 MEDA方法分类模型

首先采集不同场景下受试者的sEMG,经过预处理和特征提取获得源领域和目标领域特征矩阵,将其输入MEDA模型中,最后获得分类结果,采用MEDA方法进行手势分类的流程图如图5所示。在MEDA迁移学习模型中,首先执行流形学习,减小源领域特征矩阵与目标领域特征矩阵的数据差异,消除特征退化。然后动态调整分布差异,若数据集之间存在很大差异,两域间的边缘分布差异更为明显,若数据集是相似的,则每个类别条件分布中的差异更为显著。

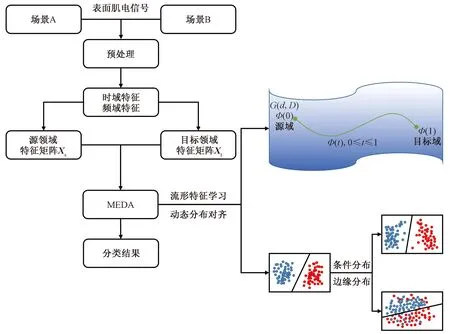
图5 采用MEDA方法进行手势分类流程图Fig.5 Hand gesture classification flow chart using MEDA method

3 实验结果及分析

3.1 性能度量

为了能够客观,全面的评价分类器的性能,采取F1分数对分类器性能进行衡量,其定义为

(7)

式(7)中:P为分类精确率;R为分类召回率;F1为F1分数,取值范围为0～1,F1取值越接近1说明分类器的性能越好。

3.2 实验结果

图6为采用MEDA方法进行手势动作四分类的混淆矩阵,可以看出,所提出的迁移学习模型可以对手势精准的进行分类。混淆矩阵图中右侧四行分别代表四类手势动作的召回率,其物理含义为在该类动作的真实次数中,模型预测正确的比重。下方四列分别代表着四类手势动作的精确率,其物理含义为模型预测为该类动作次数中,预测正确的比重。采用MEDA方法进行手势动作四分类,每种手势动作的召回率与精确率都可以达到90%,其中五指伸展动作的召回率最高,达到96.8%,ok伸展动作的精确率最高,达到96.3%。

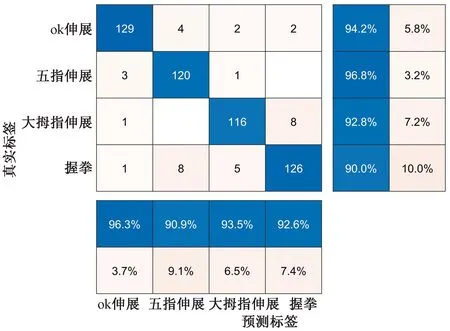
图6 MEDA方法四分类混淆矩阵Fig.6 MEDA method four classification confusion matrix

得到MEDA方法对四类手势的召回率与精确率后,采用决策树(decision tree,DT)、支持向量机(support vector machine,SVM)、k临近(k-nearest neighbor,KNN),3种传统机器学习分类器与未执行流形特征学习与动态分布对齐的JDA迁移学习方法与本研究提出的MEDA迁移学习模型进行对比,5种分类器的精确率、召回率、F1分数如图7所示。可以看出,采用MEDA方法取得的精确率、召回率、F1分数都要高于其他分类器,5种分类器的F1分数(均值±标准差)分别为0.805±0.014、0.72±0.034、0.846±0.027、0.408±0.089、0.934±0.016。与3种传统机器学习方法相比,MEDA方法的F1分数均有提升,与未执行流形特征学习与动态分布对齐的联合分布适配(joint distribution adaptation,JDA)方法相比,MEDA方法的F1分数提高了0.526,这证明了流形特征学习与动态分布对齐的重要性。

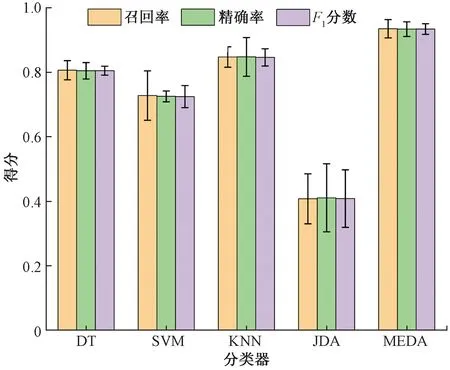
图7 5种分类器分类性能对比Fig.7 Comparison of classification performance of five classifiers

进行域适应学习后不同特征维度的手势识别F1分数如图8所示,可以看出,相比于JDA方法,MEDA方法的分类性能要更加优秀,随着维度的增长,MEDA方法的分类性能逐步提高,在维度为12时,MEDA方法的F1分数达到最高。JDA方法与MEDA方法旨在解决迁移学习中的域适应问题,即通过寻找共性知识减小源领域与目标领域之间的数据差异。

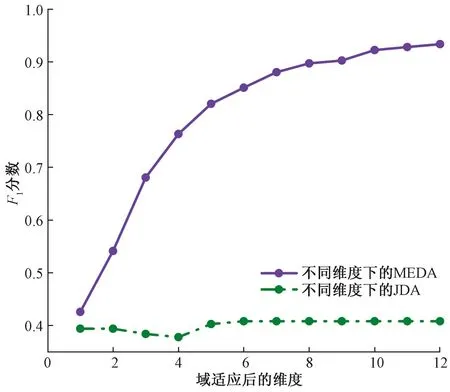
图8 不同维度下的分类性能变化Fig.8 Classification performance changes in different dimensions

JDA方法在寻找两域间的共性知识时,通过TCA方法将两域间的数据投影到高维再生核希尔伯特空间进行特征学习,TCA方法只能减小两域数据间的边缘分布差异,而对数据间的条件分布差异没有影响,所以F1分数可能上升也可能下降;此外,对F1分数起良性作用的特征值数值在经过TCA方法后可能会发生变化,此时TCA方法对F1分数提升将会带来负面效果,也就是没有解决特征退化问题。JDA方法总是把边缘分布与条件分布视为同等重要,即不考虑源领域和目标领域间的数据差异,总是将μ的取值设为0.5,因此JDA方法的F1分数较低。

MEDA方法获得二者共性知识时,通过GFK方法将数据嵌入格拉斯曼流形空间内进行学习,构建源领域和目标领域间的测地线流,将原始特征转换到无限维特征空间,解决了特征退化问题。通过动态分布对齐来解决两域间的边缘分布与条件分布比重,根据分布的差异来进行来动态衡量二者之间的重要性。当两域的数据差异较大时,着重考虑边缘分布差异,当数据差异较小时,则着重考虑 条件分布差异。在MEDA方法中,执行流形特征学习后维度越高所学习到的共性知识越多,模型分类性能越好。MEDA方法相比于JDA方法随维度变化的F1分数提升效率如表3所示。

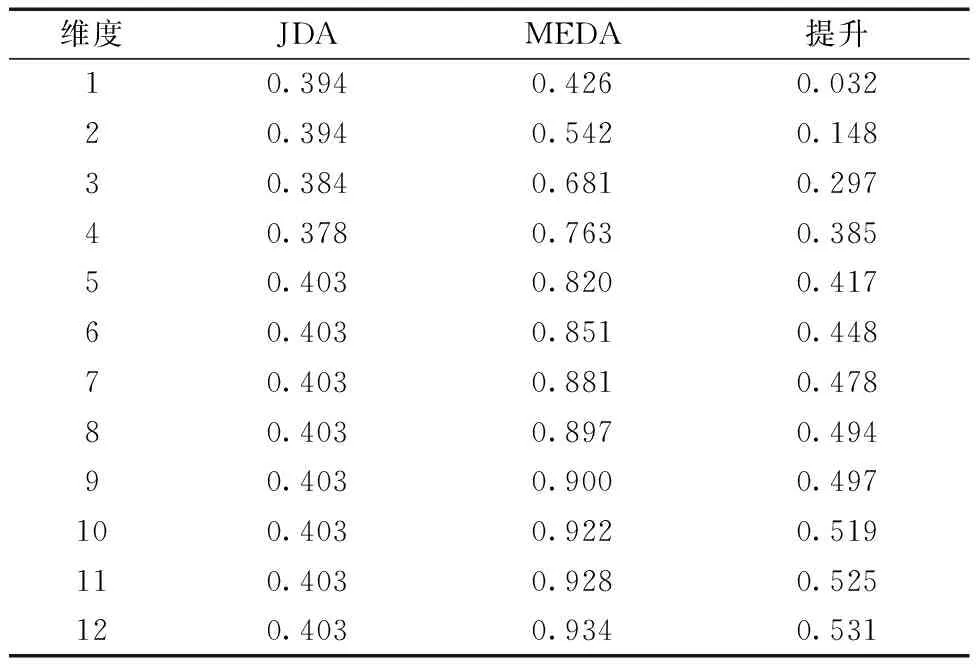
表3 MEDA方法F1分数提升效率Table 3 MEDA method F1 score improvement efficiency

4 结论

研究手部离散动作分类,为了提高电极贴片位移、受试者动作变化等复杂情况下的手势分类识别准确率,提出一种基于迁移学习的分类模型。通过MEDA方法将数据嵌入到格拉斯曼流形空间内执行流形特征学习,解决特征退化问题;提出自适应因子来应对不同情况下的分布差异,动态调整数据不同分布差异下边缘分布和条件分布的相对重要性。对多名受试者开展实验,实验结果表明用于手势分类的MEDA方法表现优异,相比DT、SVM、KNN 3种传统机器学习方法,F1分数分别提高了0.13、0.21、0.09。相比未执行流形学习和动态调整分布对齐的JDA方法,F1分数提高了0.52,有效地提高了在复杂情况下手势分类的准确率。