基于改进PSO-BP神经网络的网络控制系统时延预测

魏天旭 赵燕成 赵景波 胡阵

文章编号：2096-398X2024）03-0158-08

（青岛理工大学 信息与控制工程学院， 山东 青岛 266520）

摘 要：针对网络控制系统存在的随机时延问题，本文基于BP神经网络Back Propagation Neural Network，BPNN）建模方法，在PSOParticle Swarm Optimization）算法的基础上引入遗传算法中交叉和变异的思想，同时对惯性权重和学习因子采用线性递减和异步时变的改进策略，提出了一种性能更优的改进PSO算法，并用该算法优化BP神经网络，构建了一种改进PSO-BP神经网络的时延预测模型；然后运用MATLAB TrueTime2.0工具箱搭建仿真平台，结合获取到的历史时延采样数据对改进PSO-BP时延预测模型和PSO-BP、BP模型进行性能对比测试.实验表明本文所提出模型的预测精度更高，误差更小，能较好的解决网络控制系统的随机时延预测问题.

关键词：网络控制系统； PSO算法； BP神经网络； 网络诱导时延； 时延预测

中图分类号：TP273    文献标志码： A

Delay prediction of network control system based on improved PSO-BP neural network

WEI Tian-xu， HAO Yan-cheng， HAO Jing-bo*， HU hen

School of Information and Control Engineering， Qingdao University of Technology， Qingdao 266520， China）

Abstract：To address the problem of stochastic delay in network control systems，this paper introduces the idea of crossover and variation in genetic algorithm based on the PSO algorithm，and uses a linear decreasing and asynchronous time-varying improvement strategy for inertia weights and The improved PSO algorithm with better performance is proposed，and the BP neural network is optimized with this algorithm to construct an improved PSO-BP neural network delay prediction model; then the MATLAB TrueTime2.0 toolbox is used to build a simulation platform and combine the obtained historical delay sampling data to improve the PSO-BP neural network delay prediction model and the PSO-BP neural network delay prediction model.BP delay prediction model and PSO-BP，BP model for performance comparison test.The experiments show that the proposed model has higher prediction accuracy and smaller error，which can better solve the stochastic delay prediction problem of network control system.

Key words：network control system； particle swarm algorithm； BP neural network； network induced delay； time delay prediction

0 引言

隨着通信、计算机网络以及控制理论等技术的不断发展融合，网络控制系统（Networked Control Systems，NCS）也随之产生，并被广泛运用到各类控制领域中.相比于传统控制系统，网络控制系统可靠性更高、维护更方便，还可以实现资源共享和远程操控.但因为引入的网络具有一定的带宽限制，所以在数据传输的过程中，不可避免地会出现流量拥塞，产生随机时延，这不仅会降低系统的性能，甚至会影响系统的稳定性.而由于随机时延具有不确定性，之前的控制方法已不再适用，因此时延问题已成为NCS的难点之一［1，2］.

近年来，神经网络以其良好的学习能力成为许多领域的研究热点，国内外相关学者也都结合神经网络对NCS中存在的随机时延问题做了大量研究.文献［3］将RBFRadial Basis Function）神经网络和PSO算法PSO-RBF）作为时延预测器应用于网络控制系统中，对系统传输时延进行预测，同时结合在线RBF预测控制器实时补偿延迟，以减小延迟对系统输出的不确定性影响；文献［4］针对高速列车控制信号传输过程中产生的时延，基于自适应量子粒子群优化算法，提出了一种最小二乘支持向量机时延预测模型；文献［5］针对一类长时延系统，通过设计RBF神经网络预估器对其时延采样值进行预测，使原系统变得无延迟，并给出了神经网络的具体预测公式；文献［6］将BP神经网络与NCS相结合，提出了一种基于变周期采样的网络控制系统建模方法，仿真结果表明该方法可极大程度减轻时延影响；文献［7］将多个不同的单独模型形成一个组合模型，提出用最优权重算法通过拉格朗日乘子法最小化预测误差，计算出合适的分量模型权重系数，从而提高预测性能.

综上，为了进一步提高系统的预测精度，本文通过引入BP神经网络来解决网络控制系统的时延预测问题.BP神经网络具有函数逼近能力好、泛化能力和鲁棒性强等优点，但比较依赖初始权值和阈值.为此，本文将PSO算法和遗传算法相结合，提出了一种改进PSO算法，该算法能够自适应的调整粒子的交叉和变异概率，克服了PSO算法容易早熟的缺点，然后搭建了一种改进PSO-BP 神经网络预测模型，进而有效提升神经网络的收敛速度和精度，强化网络性能，最后通过测试函数对比实验、时延预测实验及预测误差对本文所提出方法的优越性进行验证.

1 问题分析

在网络控制系统中，各节点通过网络进行通信，由于硬件设施和网络带宽的限制，难免会出现时延和丢包问题，而在实际应用中，通过编写合适的通信协议可以有效避免丢包，因此，传输时延成为设计网络控制系统的首要问题［8，9］.网络控制系统整个控制回路的时延主要由数据传输时延和节点执行时延组成，其中数据传输时延为反馈通道时延τsck和前向通道时延τcak，节点执行时延为控制器的计算时延τck，则总时延可表示为：

τk=τcak+τsck+τck（1）

随着硬件和算法的加强，控制器计算时延τck对系统的影响可以忽略不计；反馈通道时延τsck可以通过时钟同步和在传感器发送的数据中打上时间戳的方式算出；前向通道时延τcak对控制器来说是即将发生的时延，无法利用控制器进行计算，本文主要就是对该部分时延进行分析和预测.

设网络控制系统的控制对象为连续系统，状态空间方程可表示为：

t）=Axt）+But）

yt）=Cxt（2）

式（2）中：xt）∈Rn为被控对象状态，ut）∈Rm为系统输入，yt）∈Rp为系统输出，A、B、C为常数矩阵.

为了方便对系统进行建模，需要做出如下假设：

（1）传感器节点选择时间驱动，这意味着控制系统的采样周期是相同的.

（2）控制器节点和执行器节点都选择事件驱动，这意味着信息到达节点的时间即为对应节点上设备的运行时间.

（3）无丢包、时序错乱.

（4）每个时刻的网络传输时延小于采样周期.

对于采样周期为h的系统，其离散状态方程可表示為：

xk+1）h）=Φxkh）+Γ0τk）ukh）+Γ1τk）uk－1）h）

ykh）=Cxkh）（3）

式（3）中：

Φ=eAs

Γ0τk）=∫h－τk0eAsdsB

Γ1τk）=∫hh－τkeAsdsB（4）

2 理论基础

2.1 BP神经网络

BP神经网络是一种有导师学习的多层前馈网络模型，具有结构简单、非线性拟合能力强等优点，经过多年的发展，目前已成为应用最广泛的网络模型之一.网络主要由输入层、一个或多个隐含层和输出层三部分组成，通过梯度下降法持续对权值和阈值进行调整，使得最终输出值与实际值差异最小［10］.

网络首先将信号进行正向传递，从输入层到隐含层，再到输出层，各层之间的关系仅对下一层产生作用；若无法获得期望的结果，则将其与期望值进行比较，得到的误差再逆向传递；然后通过对权阈值等参数的调节，使得网络的预测结果不断向期望输出靠拢.

2.2 标准粒子群算法

粒子群优化算法是一种适应于多维空间非线性函数优化的群智能搜索算法，算法在初始化阶段会生成一组随机的粒子，每个粒子都代表一个解，这些粒子会在解空间内移动形成一个种群，经过多次迭代完成全局寻优［11］.

假设粒子在N维空间中寻找最优解，有M个粒子，则种群可表示为X=［X1，X2，…，XM］，粒子的位置可表示为Xi=［xi1，xi2，…，xiN］T，粒子的速度可表示为Vi=［vi1，vi2，…，viN］T，粒子的个体极值为Pi=［pi1，pi2，…，piN］T，粒子的群体极值为G=［g1，g2，…，gN］T.在每次迭代过程中，其第n维1≤n≤N） 空间的速度和位置可根据以下公式进行更新：

vk+1in=wvkin+c1r1pkin－xkin）+c2r2gkn－xkin）（5）

xk+1in=xkin+vk+1in（6）

式（5）中：w是惯性权重，其大小决定了算法的搜索步距，取值范围一般在［0，1］；c1和c2是学习因子，其大小决定了粒子向个体极值和群体极值学习的能力，取值范围一般在［1，2］；r1和r2是两个随机数，取值范围在［0，1］；k是当前迭代次数.

从迭代公式可知，主要由三个因素决定粒子的速度更新.第一个是wvkin，代表粒子先前的趋势，是其惯性表现，用来调整粒子的搜索能力和收敛速度；第二个是c1r1pkin－xkin），表示每个粒子的“自我认知”，包含了粒子本身在迭代过程中学到的“经验”，可以防止种群出现早熟现象；第三个是c2r2gkn－xkin），表示整个种群的“社会认知”，包含了先前迭代过程中整个种群所学到的“经验”，可以提高粒子的全局搜索能力.

粒子群算法的寻优迭代过程如图1所示.

2.3 改进PSO优化算法

标准粒子群算法具有收敛速度快、识别过程短等优点，但当优化问题较为复杂时，算法容易收敛于局部极值而无法达到全局最优解，由式（5）和式（6）可知，当xkin=pkin=gkn时，粒子的飞行速度仅受wvkin的影响；若vkin≠0，则xk+1in≠xkin（xkin为第k次迭代中第i个粒子的位置），粒子将偏离原有的飞行轨迹，若vkin=0，则vk+1in=0，当所有该类粒子到达gkn，粒子将停止飞行，并且收敛于局部最优解，从而使算法出现早熟现象［12，13］.因此，如何充分利用粒子间的有效信息，使粒子在保持种群多样性的同时，可以用较快的速度到达最优区域，是提高 PSO 算法性能的一个关键问题.

遗传算法Genetic Algorithm，GA）具备搜索过程简单、可扩展性强等优点，算法通过选择、交叉和变异操作进行搜索，在寻找最优解方面具有很大的优势，其中交叉操作体现出信息交换的思想，可以改进种群的分割策略，变异操作能够提高种群的复杂性，从而降低迭代过程中早熟问题的发生［14］.因此，本文通过引入GA算法中的交叉和变异操作来改善PSO算法的早熟问题，提出了一种性能更好的改进PSO算法.

为了提高改进PSO算法的优化性能，首先对PSO算法主要参数的学习策略进行改进［15-17］，针对惯性权重w，主要的改进策略有线性递减法、非线性调节法和自适应调节法等，本文采用的是线性递减法，该方法可以使算法在不改变复杂度的情况下，使前期的w值较大、后期的w值较小，这样既保证了算法迭代初期的全局搜索能力，又能避免迭代后期收敛于局部最优解，迭代公式如式7）所示：

wt）=wmax－wmax－wmin）ttmax（7）

式7）中： t和tmax分别为算法当前迭代次数和最大迭代次数；相关研究表明，当wmax=0.9，wmin=0.4时，粒子群的收敛效果最好［18］.

针对学习因子c1和c2，不同于传统的在迭代过程中始终保持不变的学习策略，本文采用异步时变的方式对学习因子进行优化，使c1在不断减小的同时c2不断增大，c1不断减小可以加强粒子在迭代初期的全局搜索能力，避免粒子陷入局部范围； c2不断增大可以避免粒子在搜索过程中出现“早熟”现象，加强了粒子的全局寻优能力， 改进以后的公式如式8）所示：

c1=c1i+c1f－c1i）kkmaxc2=c2i+c2f－c2i）kkmax（8）

式8）中：c1i、c2i为学习因子的迭代初始值，k为当前迭代次数，c1f、c2f为学习因子的迭代终止值， kmax为最大迭代次数.

对于交叉操作，首先使粒子随机配对，然后按照概率pc发生交叉，交叉粒子xi、xj的位置和速度更新公式如式9）、10）所示：

xk+1i=α1xki+1－α1）xkj

xk+1j=1－α1）xki+α1xkj（9）

vk+1i=α2vki+1－α2）vkj

vk+1j=1－α2）vki+α2vkj（10）

式9）、10）中：α1、α2为［0，1］内的两个随机数.

对于变异操作，假设Pbest在第n维的取值为Pnbest，本文通过对Pnbest施加随机扰动β的方式使粒子按照pm的概率进行变异，变异公式如式11）所示：

Pnbest=Pnbest1+0.5β）（11）

式11）中：β为满足期望是0，方差是1的高斯分布.

其中，对交叉和变异概率pc、pm的选择是影响算法优化能力的主要因素之一，研究表明，交叉、变异概率取值与种群的收敛程度有关［19］，种群收敛集中时，应增大pm 、减小pc；反之，应增大pc 、减小pm.因此，本文采用了一种自适应交叉、变异方案，能够根据种群进化状态自动调整pc和pm值，改进后的公式如式12）和式13）所示：

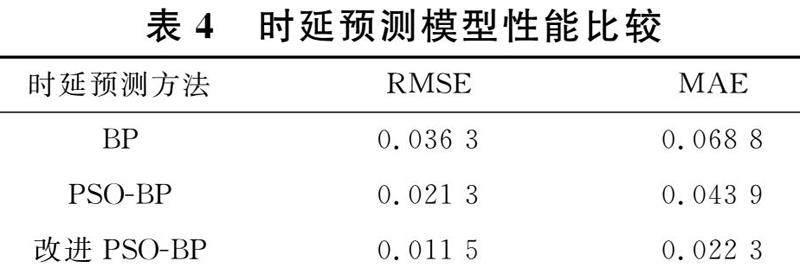
pc=pc1－pc1－pc2）fc－favg）fmax－favg，fc≥favgpc1，fc

pm=pm1－pm1－pm2）fm－favg）fmax－favg，fm≥favgpm1，fm

式12）、13）中：pc1、pc2、pm1、pm2为常量，fm为变异粒子的适应度值，fc为交叉运算的粒子中适应度较高的值， favg为种群的平均适应度值，fmax为种群的最大适应度值.从式中可以看出，适应度值比favg低的粒子更容易发生交叉和变异操作，从而保证了种群的多样性；当fmax－favg减小时，种群容易陷入局部最优解而难以跳出，此时pc和pm的值将会增加，有效提高了跳出局部最优解的能力.

为了验证本文所提出算法性能的优越性，选择Sphere和Rastrigin两种测试函数对改进PSO 算法和标准PSO 算法进行对比实验，其中，单峰函数Sphere可以评价算法的收敛效率，多峰函数Rastrigin可以测试算法的“早熟”情况.具体的函数表达式和图像如表1及图2、图3所示.

为了实验更精确，现做出如下规定：标准PSO算法中，w设为0.8，c1和c2設为1.5；改进PSO算法中，wmax设为0.9，wmin设为0.4，c1的取值范围在［1，2.5］，c2的取值范围在［1.5，2.75］；种群数量设为20，算法迭代次数为1 000，分别对两种算法进行20次实验，记录其平均值，仿真结果如表2所示.

由表2可知，在两种测试函数中，改进PSO算法的适应度值、方差和迭代步数三个指标均优于标准PSO算法，具有更好的收敛精度和速度.

3 改进PSO-BP算法实现

为解决网络控制系统产生的随机时延问题，本文运用改进后的PSO算法对BP神经网络进行优化，提出了一种改进PSO-BP神经网络预测模型，算法具体步骤如下：

步骤1 初始化神经网络.确定BP神经网络的各层结构.

步骤2 初始化种群.确定种群的规模和维度，初始化粒子的速度和位置，设定迭代次数.

步骤3 计算粒子适应度值.以均方根误差作为适应度函数，以此评价算法性能，如式14）所示：

f=1D［∑Dk=1τk－[Aτ^]k）2］（14）

式14）中：D为预测总次数；τk为第k次测量到的延迟；[Aτ^]k为第k次预测的延迟.

步骤4 粒子群迭代.分别根据式5）和式6）更新粒子的速度和位置，得到新种群.

步骤5 交叉变异操作.新种群中的粒子先以概率pc进行两两交叉操作，再以概率pm对适应度值差的粒子进行变异操作.

步骤6 更新个体极值Pbest、群体极值Gbest和最优适应度值.若算法达到最大迭代次数或者训练误差小于规定误差，则停止迭代，把结果保存起来；否则返回步骤3.

步骤7 利用步骤6保存的结果初始化BP神经网络的权阈值.

步骤8 按照结构输入数据集，对网络进行训练.

步骤9 计算预测值与实际输出之间的误差，更新权值和阈值.

步骤10 判断算法是否停止.若误差小于规定误差，则输出预测结果，训练结束；否则跳转至步骤8.

算法流程图如图4所示.

4 仿真与结果分析

4.1 时延预测模型验证

本文利用MATLAB中的TrueTime2.0工具箱搭建仿真平台，对基于BP神经网络的网络控制体系统控制性能进行仿真验证.考虑建立以下伺服控制系统，受控对象的传递函数为：

Gs）=1 000ss+25）（15）

网络选择IEEE 802.11b/g（WLAN）无线网络，采样周期设置为10 ms，网络速度取500 kB/s.利用该仿真平台从网络控制系统记录1 000组时延数据样本，将其中800组数据作为训练集，剩余200组数据作为测试集，为改进PSO-BP网络建立时延预测模型.经过多次试验，改进PSO-BP网络模型的各项参数设置如表3所示.

为了验证改进PSO-BP神经网络所构建的预测模型的性能，分别采用三种算法模型对时延数据进行预测.图5～8为三种不同方法的时延预测结果和预测误差.

结合图5～8，由时延预测拟合图对比可以看出：改进PSO-BP预测模型得到的预测值与期望值的拟合效果优于BP模型和PSO-BP模型，其中原始BP模型的拟合效果最差.由预测误差曲线对比可以看出：改进PSO-BP预测模型的预测值与期望值误差最小，误差相对稳定，而BP神经网络每次预测的误差波动较前一次预测更为明显，误差曲线相对复杂，无法准确预测延迟，不能满足网络控制系统的需要.

为了进一步显示不同模型的预测精度，分别选择均方根误差RMSEroot mean square error）和平均绝对误差MAEmean absolute error）来评价算法的预测性能.表4给出了不同预测模型对10个独立预测的平均预测性能.由表可以看出，改进PSO-BP 神经网络时延预测模型的RMSE和MAE分别为0.011 5和0.032 3，对比PSO-BP模型分别降低了46.0%和49.2%，对比BP模型分别降低了68.3%和67.6%，优于其他两种预测模型，表明PSO-BP模型的预测性能更好.

综上，本文所提出的改进PSO-BP网络时延预测模型具有良好的预测性能，预测值与实际值的拟合度更佳，误差更小，能够很好的解决网络控制系统的时延预测问题.

4.2 基于BP神经网络的网络控制系统控制性能分析

为了证明本文提出的基于改进PSO-BP时延预测模型的网络控制系统的实用性，与传统PID控制算法进行实验比较，具体参数设计见前述表3.其中输入信号为方波信号，仿真结果如图9所示.

由图9可以看出，针对具有随机时延的网络控制系统，本文提出的控制方法可以使系统输出更加快速精确地跟踪二阶控制对象的输出参考轨迹，并且超调和调节时间均优于PID控制算法，可以满足系统的性能要求.尽管这三种控制方法经过一段时间的调整后都能达到预期的控制效果，但在时间上，改进PSO-BP神经网络预测控制能够比BP神经网络预测控制和PID控制更快达到预期的控制效果，并且在上升和下降過程中的跟踪速度也更迅速，可以实时满足系统的需求.相比之下，BP神经网络预测控制和PID控制在上升和下降阶段后会出现一定的超调量.

为了进一步验证本文提出控制方法的控制效果，使用积分绝对误差IAE Integral Absolute Error）和时间加权积分绝对误差ITAE Integral Time-weighted Absolute Error）来评估控制效果，具体公式如下所示：

IAE=1∑t=1rt）－yt）

ITAE=1∑t=1trt）－yt）（16）

式（16）中：是采样总数，rt）、yt）分别是时间t的参考输入和控制输出.

表5为不同控制方法的性能指标对比.由表可以看出，改进PSO-BP预测控制方法的IAE和ITAE分别为0.127 1和0.101 5，对比BP预测控制分别降低了30.9%和38.9%，对比PID控制分别降低了67.6%和72.7%.因此，针对具有随机时延的网络控制系统，本文提出的基于改进PSO-BP神经网络的预测控制方法具有更好的自适应和更低的误差，并且可以实现对随机时滞更精确的预测补偿.

为了更接近实际控制环境，本文通过添加时间周期为0.5 s

不同控制方法在有扰动影响下的控制效果对比如图11所示.从图中可以看出，在加入噪声干扰后，三种控制方法的输出都出现了一定波动，和不加扰动的情况相比跟踪效果均有所下降.但本文提出的基于改进PSO-BP神经网络的控制方法在模型训练过程中考虑了外界扰动的影响，具有一定的抗干扰能力，因此在加入白噪声干扰后，跟踪曲线的波动不大，能相对平稳地跟踪设定值，并且扰动结束后的超调更小，可以满足系统的要求.而基于BP神经网络和PID的控制方法在控制过程中波动较大，对噪声干扰的抑制能力不如本文提出的控制方法.

为了验证在扰动信号作用下不同控制方法的控制效果，使用前文提到的IAE和ITAE来进行评估，结果如表6所示.由表可以看出，改进PSO-BP预测控制方法的IAE和ITAE分别为0.190 7和0.152 3，对比BP预测控制分别降低了35.3%和42.7%，对比PID控制分别降低了71.4%和75.9%.结果表明，在扰动信号的影响下，本文提出的基于改进PSO-BP神经网络的预测控制系统控制误差最小，在噪声干扰下的控制效果最优，具有更好的自适应和扰动抑制能力，可以实现对随机时延更精确的预测补偿.

5 结论

为了进一步提高时延预测的准确性，解决网络控制系统存在的时延问题，根据控制系统实时性和精确性的要求，本文将PSO算法和GA算法结合起来对BP神经网络进行优化，利用PSO算法快速收敛及GA算法全局搜索的优点，有效解决了BP神经网络容易过度拟合和收敛速度慢的问题，构建了一种基于改进PSO-BP 神经网络的时延预测模型.首先通过与标准PSO在测试函数上对比可知本文所提出算法具有更好的收敛精度和速度；其次通过与BP模型和PSO-BP模型的性能对比实验可知：基于改进PSO-BP神经网络预测模型的拟合效果最好，其预测结果与实际值最接近，且均方根误差RMSE和平均绝对误差MAE更低，对比BP模型降低了68.3%和67.6%，对比PSO-BP模型降低了46.0%和49.2%，具有更优的预测效果；最后通过与传统PID算法在不加扰动和加入扰动的情况下进行比较可知，本文所提方法的跟踪效果最好，具有更低的误差和更高的抗扰动能力，可以满足系统的要求.

现阶段仅论证了改进PSO-BP神经网络对时延预测的有效性，对时延预测之后进行补偿将会是今后进一步研究的重点.

参考文献

［1］ 游科友，谢立华.网络控制系统的最新研究综述.自动化学报，2013，392）：101-118.

［2］ hang X M，Han Q L，Ge X，et al.Networked control systems：A survey of trends andtechniques.IEEE/CAA Journal of Automatica Sinica，2019，71）：1-17.

［3］ You D，Lei Y，Liu S，et al.Networked control system based on PSO-RBF neural network time-delay prediction model.Applied Sciences，2022，131）：536.

［4］ ong X，hang T.Improved generalized predictive control for high-speed train network systems based on EMD-AQPSO-LS-SVM time delay predictionmodel.Mathematical Problems in Engineering，2020，2020：1-19.

［5］ 张 捷，薄煜明，吕 明.基于神经网络预测的网络控制系统故障检测.南京理工大学学报，2010，341）：19-23.

［6］ Yi J，Wang Q，hao D，et al.BP neural network prediction-based variable-period sampling approach for networked controlsystems.Applied Mathematics and Computation，2007，1852）：976-988.

［7］ Xu P，Wu J.A novel method for time delay prediction in networked controlsystems.International Journal of Ad Hoc and Ubiquitous Computing，2019，322）：99-109.

［8］ 陈 勇，李 猛.网络控制系统的预测控制算法研究进展.电子科技大学学报，2016，454）：564-572.

［9］ Liu ，Selivanov A，Fridman E.Survey on time-delay approach to networkedcontrol.Annual Reviews in Control，2019，48：57-79.

［10］ 楊润泽.基于 GA-PSO-BP 神经网络的车险欺诈识别研究［D］.长沙：湖南大学，2021.

［11］ Harrison  R，Engelbrecht A P，Ombuki-Berman B M.Inertia weight control strategies for particle swarm optimization：Too much momentum，not enough analysis.Swarm Intelligence，2016，10：267-305.

［12］ Modiri A，iasaleh .Modification of real-number and binary PSO algorithms for accelerated convergence.IEEE Transactions on Antennas and Propagation，2010，591）：214-224.

［13］ 刘爱军，杨 育，李 斐，等.混沌模拟退火粒子群优化算法研究及应用.浙江大学学报：工学版，2013 10）：1 722-1 730.

［14］ usztelak G，Lipowski A，ucharski J.Population symmetrization in genetic algorithms.Applied Sciences，2022，1211）：5 426.

［15］ 杨博雯，钱伟懿.粒子群优化算法中惯性权重改进策略综述.渤海大学学报 自然科学版），2019，403）：274-288.

［16］ 万海超，何 勇.基于改进PSO-BP神经网络的电锭细纱机的PID控制.制造业自动化，2023，452）：159-163.

［17］ Ermakov S M，Semenchikov D N.Genetic global optimization algorithms.Communications in Statistics-Simulation and Computation，2022，514）：1 503-1 512.

［18］ 张九龙，王晓峰，芦 磊，等.若干新型智能优化算法对比分析研究.计算机科学与探索，2022，161）：88.

［19］ 申一非，祁文哲，李德仓，等.横风下基于滚动GAPSO算法的列车速度曲线优化.铁道标准设计，2024，683）：21-28.

【责任编辑：蒋亚儒】