数学软件引入概率统计课堂教学的探索与实践

宁桂英

（柳州工学院，广西柳州 545616）

工业革命4.0 引发的快速变革，对高校人才培养提出了新的要求，在此背景下，新工科建设成为我国新时期高等教育改革的指导方针[1]。新工科的实质是培养具备较强的工程实践能力、创新能力，能够满足行业发展需求的应用型和技能型人才[2]。大学数学作为本科院校的一门重要的公共基础课程，传统教学模式已不能满足新工科需求，因此，许多学者已尝试进行改革[3-11]。

概率论与数理统计是研究随机现象统计规律的一门数学学科，具有广泛的应用性，被应用于工程技术、经济管理和预测、科学研究、企业管理等众多领域[12]，且其理论和方法对解决许多实际问题有着重要的作用。但由于该课程内容深奥抽象、公式繁多且计算复杂，传统的课堂教学难以达到学生用所学知识解决实际问题能力的培养。为了更好地满足新工科对人才的需求，有必要对概率统计课程进行教学改革。本文结合柳州工学院教学实际，探讨了将数学软件引入概率统计课堂，在激发学生学习兴趣的同时，培养学生动手能力和解决问题能力，进而提高课堂教学质量。

1 概率统计课程教学现状

概率论与数理统计是柳州工学院大学二年级理工科专业学生的一门重要的公共数学基础课，共48学时，为解决课时少、内容多、学生知识面拓宽受限等问题，采用了线上线下混合教学模式，在一定程度上提高了课堂效率，但由于没有单独开设数学实验课程，数学软件在课堂教学中的应用有限，难以很好地在课堂上动态呈现随机现象的变化规律，对一些复杂计算问题也只停留在依靠板书推导的过程，缺乏用数学软件进行演示性操作和解决具体问题的实践操作，在一定程度上限制了学生的思维，难以调动学生学习的积极性。

2 数学软件引入概率统计课堂的探索

随着教育技术的现代化和计算机软件的快速发展，计算机作为多媒体教学的辅助工具，已广泛应用于各类课堂。目前已开发出各种非常有效的统计软件，在概率统计课堂教学中有针对性地引入这些数学软件，一方面，可以帮助师生从烦琐的计算中解脱出来，更好地观察、理解、掌握基本理论和方法，调动学生学习的积极性，提高教师课堂教学效率；另一方面，教师在案例分析中通过数学软件引导学生进行数学建模，在实践中培养和提高学生发现问题、分析问题和解决实际问题的能力，帮助学生建立用数学建模方法解决实际问题的意识，学生有了实践的机会，学习兴趣显著提高。已有学者研究了在大学数学课程中引入平板电脑的优势[13]。

3 数学软件引入概率统计课堂的实践

3.1 利用数学软件对随机现象进行直观演示和解释

法国数学家拉普拉斯曾说：“生活中最重要的问题，绝大多数在实质上都是概率问题”[14]。诚然，概率论与数理统计课程中很多概念与公式的产生都源于解决生活中的问题，这些概念与公式的数学语言描述都很抽象，单一理论讲解，学生难以理解，若用Excel 或Matlab 软件进行模拟演示，可以帮助学生更好地理解公式和概念，从而更好地运用概念解决问题，弥补了传统课堂教学的不足。

如：在讲频率时，频率具有稳定性，随着实验次数的增加，频率会稳定在某具体数值附近，按照传统的教学法学生难以理解。但如果教师在课堂上动态演示抛硬币实验，通过现场实验直观观察这一稳定性，学生就能深刻理解随着实验次数的增加，频率稳定于某一具体数值的过程，为后续对概率定义的理解做好铺垫。图1 是用Matlab 模拟抛硬币100 次、1 000 次和10 000 次的过程中，动态演示硬币正面和反面出现次数的过程。

图1 抛硬币实验

中心极限定理是概率论与数理统计中一个非常重要的定理，也是比较难以理解的内容之一，在实际问题中，许多随机现象都是由大量相互独立的随机因素综合影响而形成的，其中每个因素所起作用又都是微小的，这类随机变量都服从或近似服从正态分布。而中心极限定理指出：无论随机变量服从什么分布，n个随机变量和的极限分布一定是服从正态分布的。定理内容很抽象，可以用Matlab 分别演示离散型0～1 分布和的分布与连续型均匀分布和的分布情况（见图2），引导学生观察，随机变量个数越多，和的分布就越接近正态分布，学生通过动态观察后，更易理解定理的内容。

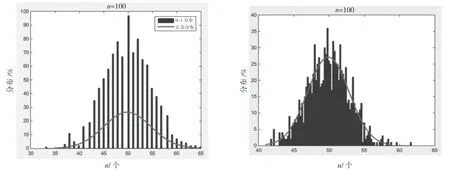
图2 随机变量的个数n 越大，和的分布越近似于正态分布

为使学生加深对中心极限定理的理解，可用该定理解释身边的现象，如：在赌博游戏里，庄家常常在两边放置值钱的东西吸引顾客，这种游戏可信吗？以高尔顿钉板实验为例，用Matlab 动态演示，如图3 所示，在演示的过程中可以看出，小球落在中间的概率远远大于落在两边的概率，即小球落入小槽的个数是呈正态分布的，这也就揭穿这个游戏的奥秘。通过计算机演示，解释了生活现象，达到学以致用的目的。

图3 高尔顿实验

3.2 设置应用型案例，强化软件应用，培养数学建模能力，增强教学内容的实效性

概率论与数理统计是研究随机现象的一门学科，在生活中有着广泛的应用。教学中挖掘概率知识在生活中的应用案例，一方面，增强学生学习的积极性，拓展知识面；另一方面，通过对实际问题的求解，培养学生数学建模能力和软件应用能力，进而提高学生的高阶思维能力，为学生后续的学习、工作奠定基础。

全概率公式和贝叶斯公式是概率论部分的重点和难点内容，公式抽象复杂，学生难以理解公式内涵。在教学中，教师用案例教学法，以“海难空难”搜救案例引入，并将概念及其应用融入案例中。如：以美军“天蝎号”核潜艇搜救为例，图4 为以Matlab模拟“天蝎号”搜救过程。

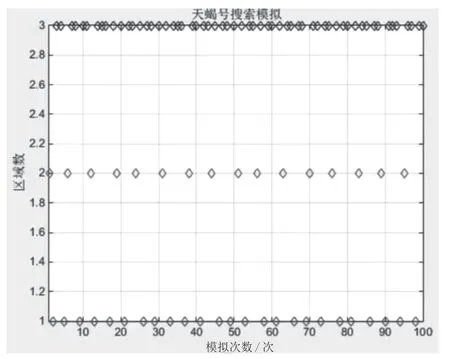
图4 Matlab 模拟“天蝎号”搜救过程

首先将实际问题数学化，简化为如下数学问题：

设“天蝎号”核潜艇沉没在甲、乙、丙3 个区域之一，潜艇技术部门判断其概率分别为1/2，1/3，1/6；搜救专家搜索这些地域，若有核潜艇，发现的概率分别为1/2，2/3，1/4；如果搜索甲区域后未找到核潜艇，“天蝎号”沉没于甲区域的概率是多少？

先从简单问题入手，设A=“搜索甲区域未找到核潜艇”，B1，B2，B3分别表示核潜艇沉没在甲、乙、丙三个区域，则

贝叶斯公式：P(B1|A)=P(AB1)/P(A)=P(B1)P(A|B1)/P(A)=1/3

接着教师引领学生深入探讨，在第一轮搜索后，“天蝎号”最可能沉没在哪个区域？启发学生用贝叶斯公式判断，在引导学生进行了两轮的计算后，学生基本掌握了贝叶斯方法的迭代过程，理解了贝叶斯公式的原理，此时进一步提问：“天蝎号”最终是如果找到的？是这样一直用手工计算下去吗？有没有简单的方法呢？面对这个复杂的实际问题，学生也很想知道用什么方法计算简单。此时启发学生可以用计算机计算，鼓励学生动手操作，通过计算机动态模拟搜救过程，能快速实现在200 次的搜索中展示搜索区域的变化情况，即形象生动，又展示了计算机计算的高效性，这种理实结合的教学方式，使学生在知识学习的过程中也掌握了获取知识的方法，学生学习兴趣高涨。学生课后反馈：不仅轻松掌握了贝叶斯公式，而且了解了贝叶斯公式的具体应用，更重要的是了解了以数学建模方法解决实际问题的基本思想，记忆深刻。

3.3 借助数学软件，实现复杂的数学计算

概率论与数理统计的教学目标之一是使学生能够熟悉数据处理、数据分析、数据推断的基本方法，并能用所掌握的方法分析和解决实际问题。在大数据时代，信息资源越来越丰富，在用数理统计知识处理实际问题时面对的数据量也越来越庞大，需要借助计算机软件来计算。在Matlab 的统计工具箱中，提供了常见的样本求解函数，操作简单，容易实现，如样本均值、样本方差的计算，点估计的计算等。教师在数理统计部分的教学中适当介绍Matlab 的应用，可简化样本处理的计算过程，增加课堂活力，拓宽学生眼界，提高课堂教学效率，同时也为学生进一步利用软件处理大数据能力的培养奠定基础。

在求解样本均值时，调用mean 函数，直接返回样本平均值；调用var 函数，返回样本无偏估计的方差；调用mle（‘norm’,x,0.05）格式，返回正态分布的置信水平为95%的置信区间；调用ztest 函数，可实现在方差已知情况下对总体均值的检验，而在方差未知时可调用ttest 函数对均值进行假设检验等，实践证明：正确运用Matlab 软件，不仅可避免繁琐的计算，而且调动了学生学习的积极性，学生也有动手实践的机会，增加了数学课堂的趣味性。

3.4 数学软件引入教学，促进学生核心素养的培养

数学软件的引入，提高了课堂效率，在此情况下组织课堂教学内容、设置教学案例、设计教学活动等都对教师提出了更高的要求。教学内容的组织安排、教学案例的挑选、教学活动的设计旨在促进学生核心素养的培养，为学生后续的学习和发展奠定坚实的基础。数学建模是根据实际问题来建立数学模型，然后利用软件对数学模型进行求解，最后根据计算结果解决实际问题。因此，将数学建模思想引入课堂，通过设置解决实际问题的教学案例，引导学生用所学知识分析、建模，并用数学软件求解，不仅实现了教学模式和教学方法的创新，而且使学生学会了主动思考和动手实践，在这个过程中，学生的创新精神和创新能力都得到了培养，逻辑思维能力和软件应用能力也得到锻炼和提升，真正实现了以学生为主体的教学理念。同时在教学中，深入挖掘数学概念、教学案例中的课程思政元素，使学生在学习数学知识的同时得到思想的启发和教育，可促进学生核心素养的培养，教学效果显著。

4 数学软件引入概率论与数理统计课程的实践效果

笔者将数学软件引入概率论与数理统计课堂教学，通过近两年的教学实践，学生反馈：提高了数学兴趣，被数学的魅力吸引，增强了数学建模解决实际问题的意识，提高了动手能力和软件应用能力。相对于传统课堂教学，学生学习兴趣提升，课外学习情况明显好转，课堂教学质量明显提高。学生分析问题、解决问题的能力得到提升，在各级各类数学建模竞赛中多次打破纪录，创造佳绩。这些充分证明将数学软件引入概率统计课堂，能够顺应新时代教育教学要求，符合学生发展需求，值得推广。

5 结束语

本文以在新工科背景下高校人才培养目标为出发点，改革教学内容、教学模式和教学方法，强化统计思想和方法的理解，突出知识的运用，这些改革措施依托数学软件的引入来实现。将数学软件引入概率论与数理统计课程的教学，能够简化烦琐的手工计算，实现了理论教学与实践教学的有机结合，实践证明：改革后的教学方法新颖，教学内容更加直观清晰，易于理解，课堂教学效率高。教无定法，需要因材施教，要想达到满意的效果，需要教师认真钻研教学素材，精心组织教学，从人才培养角度考虑，将数学软件引入课堂是教学改革的趋势，值得广大数学教学工作者探索和思考。