平行四边形的定义、性质与判定
田载今
认识一种几何图形,通常有如下过程:首先要研究它的定义,即明白它是什么样的图形,这种图形最基本的特征是什么:其次要研究它的性质,即弄清除定义给出的最基本特征之外,这种图形还具有哪些特性:最后要研究它的判定,即除用定义之外,还可根据什么条件认定一个图形是这种图形.在认识平行四边形时,同学们会经历上述过程,并能完整地体会认识几何图形的三部曲.
一、平行四边形的定义
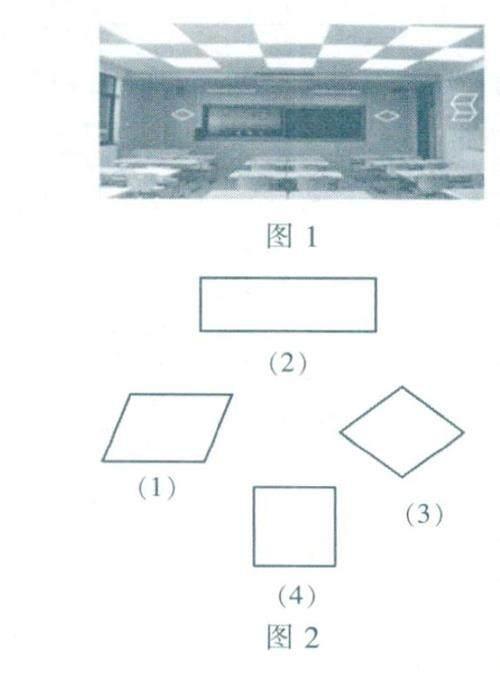
四边形是四条线段首尾相连形成的多边形,其中有一种四边形的两组对边分别平行.现实世界中,这种四边形的原型不胜枚举,图l是某教室的场景,从中能抽象出多个不同的这种四边形(图2).
平行四边形的定义:两组对边分别平行的四边形叫作平行四边形.这个定义的构成形式是以四边形为基础,再加上“两组对边分别平行”这一条件(可称它为定义条件).因此,平行四边形是满足定义条件的一种特殊的四边形.一种图形的定义,是用简明的文字对这种图形加以描述与限制,它给出_r能确定这种图形的最基本的特征,南平行四边形的定义可知,若在四边形ABCD中,AB// CD,AD//BC,则四边形ABCD是平行网边形,可表示为□ABCD.反之,在□ABCD中,一定有AB//CD,AD//BC.茌平行四边形的定义中,“两组对边分别平行”是平行四边形最基本的特征,也是它最根本的属性,即本质的内涵.这种“基础概念(如四边形)+本质内涵(如两组对边分别平行)”形式的定义,叫作内涵式定义.
再看以下几个定义:有一个角是直角的平行四边形叫作矩形(图2(2));一组邻边相等的平行四边形叫作菱形(图2(3));有一个角是直角,并且有一组邻边相等的平行四边彤叫作正方形(图2(4)).这三个定义都是内涵式定义,它们都是以平行四边形为基础概念,又分别加上一些不同的定义条件(本质内涵).因此,矩形、菱形和正方形都是特殊的平行四边形.
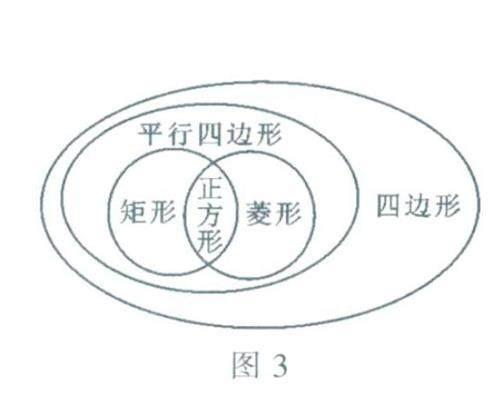
这些四边形的包含关系如图3所示,其中最大的圈表示四边形所含范围,其余各圈都含其内:平行四边形属于四边形,矩形、菱形都属于平行四边形:正方形用最小的圈表示,它被包含在矩形和菱形中,是两者的公共部分.
图3表示了这些图形的外延,即所含对象的范围,四边形外延最大:其次是平行四边形,它是特殊的四边形:矩形和菱形是特殊的平行四边形,它们的外延有分有合,其公共部分为正方形:正方形既是特殊的矩形又是特殊的菱形,也是特殊的平行四边形.
二、平行四边形的性质
平行四边形是特殊的四边形,因此平行四边形具有四边形的所有元素和性质,包括有四条边、四个角、两条对角线,内角和为3600等,此外,“两组对边分别平行”是四边形未必具有,而平行四边形一定具有的最基本特征和最根本属性,由它还能进一步得出平行四边形定义中虽没直接给出但隐含于其中的其他属性,包括“对边相等”“对角相等”“对角线互相平分”“两对角线的平方和等于四条边的平方和”等.这些就是平行四边形的性质,它们是建立在定义的基础上,经推导论证所得的重要结论.
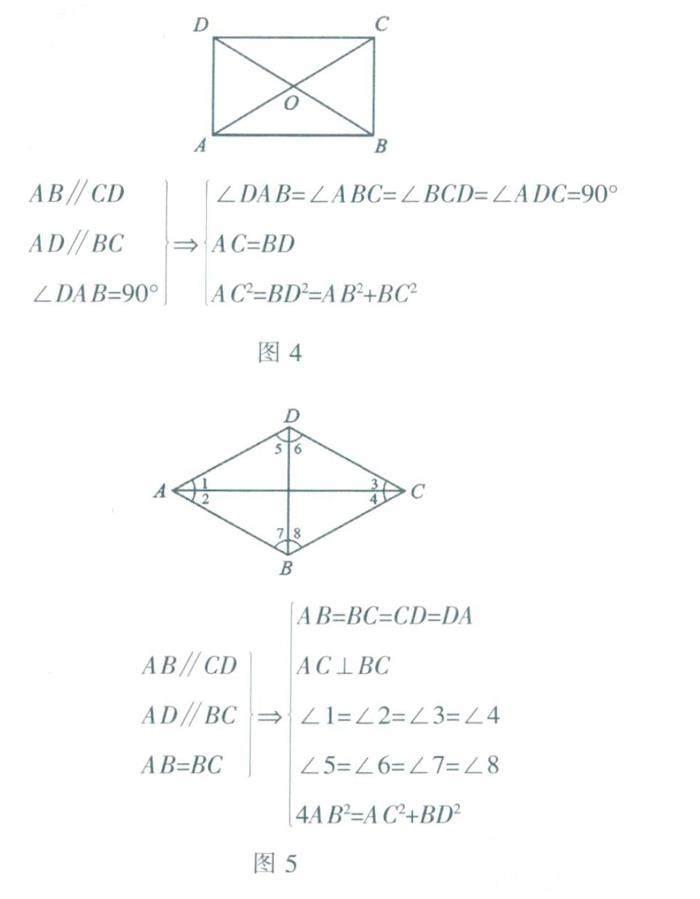
对于矩形、菱形和正方形这些特殊的平行四边形,分别依据它们各自的定义,可以推出它们除具有平行四边形的所有性质外,还具有的自己的一些特性,矩形还具有特性:“四个角鄙是直角”“两条对角线相等”“每条对角线的平方等于两邻边的平方和”等(图4):菱形还具有特性:“四条边相等”“对角线互相垂直”“对角线平分对角”“边长平方的4倍等于两对角线的平方和”等(图5);正方形既是矩形又是菱形,因此它具有矩形和菱形的所有特性,
掌握图形的性质,是认识和解决图形问题所必需的,图形的所有性质都由图形的定义确定,定义中已经隐含而未直接表述的性质,都可以从定义出发逐步推出.
三、平行四边形的判定
研究平行四边形的判定,即找出一个图形满足哪些条件时,就可以确定它足平行四边形.如前所述,利用平行四边形的定义可以进行判定.此外,还可以通过考察一个图形是否满足平行四边形定义以外的另一些条件,来完成这样的判断.这样的条件叫作判定条件.判定条件是与定义条件等价的条件,它们与定义条件可以互相推导.当一个四边形满足“两组对边分别相等”,或者“两组对角分别相等”,或者“两条对角线互相平分”,或者“一组对边平行且相等”中的任何一个条件时,都可以推导出“两组对边分别平行”,从而判定这个四边形是平行四边形(图6).这些条件都是平行四边形的判定条件,
需要指出,平行四边形一定具有的性质,不一定都能成为平行四边形的判定条件.例如,虽然容易证明平行四边形被其一条对角线分为两个全等三角形,但满足条件“能被一条对角线分为两个全等三角形”的四边形不一定是平行四边形.例如,图7中的四边形被一条对角线分为两个全等的三角形,但这个四边形显然对边不平行,故不是平行四边形.
有人可能会想:既然判定条件与定义条件等价,两者可以相互推导,那么能否把平行四边形的定义改为“两组对边分别相等的四边形”,或者“两组对角分别相等的四边形”,或者“两条对角线互相平分的四边形”呢?一种图形的定义是根据它的某种本质属性给出的,这是研究它的出发点.因此,在关于这种图形的知识体系中,定义是唯一的,如果把上述判定条件之一改为定义条件,尽管由新、老定义得到的对象完全相同,都是平行四边形,但老定义是由人们发现了这种图形中“平行”这一明显的直观特征而产生的,这样下定义便于理解,这种图形的名称也由此而来.因此,原有的定义更好,它的叙述简明且符合人们由简单到复杂、由直观到抽象的认知规律和习惯.
要判定矩形、菱形和正方形这些特殊的平行四边形,除依据它们各自的定义之外,还可以利用它们各自具有的特性.例如,矩形的判定条件有“三个角都是直角的四边形”“两条对角线相等的平行四边形”等:菱形的判定条件有“四条边相等的四边形”“对角线互相垂直的平行四边形”“对角线平分对角的平行四边形”等:正方形的判定条件有“各边相等且各角相等的四边形”“对角线相等且互相垂直平分的四边形”等.由这些判定条件都可以推出它们满足相应图形的定义,这些判定条件都与相应定义等价,例如,有时需先证一个图形是平行四边形,再证它有一个角是直角或一组邻边相等,从而判定它是矩形或菱形,这是根据定义判定;有时直接证四边形四个角相等或四条边相等,即可判定它是矩形或菱形,这是利用性质判定.
综上所述,对图形的定义、性质与判定的关系可以概括如下:定义给出了一种图形独具的某种基本特征:由定义又能进一步推H{这种图形满足的另一些数量关系或位置关系,它们构成这种图形的性质;所有这種图形都能满足,而其他图形都不能满足的数量关系或位置关系,就成为这种图形的判定条件,

