数学史融入数学教学的诠释学模式探索

①基金项目：四川省哲学社会科学重点研究基地彝族文化研究中心资助项目“数学文化融入彝族预科学生数学课程教学的研究”（YZWH2029）；四川省哲学社会科学重点研究基地彝族文化研究中心资助项目“凉山高校彝汉‘一类模式民族预科教育研究”（YZWH1926）。

作者简介：罗炯兴（1985—），男，汉族，四川阆中人，硕士研究生，讲师，研究方向：数学教育。

［摘           要］  在现有研究成果的基础上，联系数学史融入数学教学实际，对现行双循环诠释学模式进行分析和探索， 并结合教科书、数学史、学生实际水平、教学现实条件四个因素， 提出了一种数学史融入数学教学的多向循环诠释学模式。这种诠释学模式比较全面地考虑了数学教学各环节要素之间的相互联系， 能够更好地探索数学史融入数学教学的恰当角度和方式， 在实践中更好地指导数学教学，充分发挥数学史的教育价值。

［关    键   词］  数学史；数学教学；诠释学模式；探索

［中图分类号］  G642                   ［文献标志码］  A                   ［文章编号］  2096-0603（2024）12-0０29-04

一、前言

第八届全国数学史与数学教育（HPM）学术研讨会，于2019年5月10—12日在上海交通大学闵行校区举行，该届HPM学术研讨会暨第十届中国数学会数学史分会学术年会同期举行，该届HPM学术研讨会的报告内容涉及张奠宙先生纪念、HPM理论探讨、HPM教学实践、教育取向的历史研究、HPM与大学数学教育、数学文化与数学教育6个主题，显示了现阶段国内HPM研究的特点：数学史与数学教育的实践案例增多；数学史与数学教育的研究范围拓广；数学史与数学教育研究学段广泛[1]。该届HPM学术研讨会的报告汇集国内研究的最新成果，集中反映了当前研究的特点，具有一定的参考价值，为未来的HPM研究提供了启示和方向。

1972年HPM成立以后，数学史融入数学教学的研究是HPM研究的重要领域，其中教育取向的数学史研究、基于历史发生原理的教学法研究和数学史融入课堂的教学实验研究一直是HPM研究的热门话题。2000年以来，数学史融入数学教学一直是历届HPM大会的主题之一，研究者不仅在经验层面描述数学史的融入，更多地在理论层面和应用理论指导教学实践层面研究有关的历史模块，课堂设计、教学案例和课堂实验，研究成果对数学教学实践有了更强的指导性和适用性[2]。

但是，对数学教师而言，数学史融入数学教学的方式并不是一个很容易解决的问题。纵观历史上重要数学思想、理论及其方法等产生和发展过程有着自己的特殊历史背景和规律，有启发的思想并不能帮助教师解决如何有效地构造教学环节中的实践问题[3]。事实上，纵观数学的发展历史，数学始终是知识不断交替更新、总结归纳、来源于实践并应用于实践及其服务于人类社会发展的系统化动态过程，并一直持续着，不断前进。在数学教学中，若要体现数学史的积极促进作用，需要把数学史融入数学教育的整体框架之中，综合考虑数学史与诸多教育要素之间的关系，恰当地将数学史融入数学教育中的各个教学环节。在这样的背景下，数学史融入数学教学的有效方式、途径及其策略，将是首先急需解决的一个问题，数学史融入数学教学模式的研究就成为一个特别值得关注的课题。

二、数学史融入数学教学的研究现状

尽管不少研究者和数学教育组织对数学史融入数学教学给予了充分的肯定，也有一些研究者对此提出一些理论和实践上的质疑[4]。

（一）从理论上对数学史融入数学教学的质疑

针对数学史融入数学教学，Radford[5]，Ungurn[6]和Fried[7]等学者指出，现代的数学教育与已经发生的数学史及其产生的历史方法等之间，对数学教学的方法和理念等有可能产生不协调。简单地说，一方面，不同层次的数学课程（含中小学、大学、高职和民族预科等）的课程目标为今后的数学进一步学习打好基础。当使用数学史来辅助实现数学课程目标及价值定位，并制定数学教学实践和过程，就不可避免产生一种“时空错置”现象；另一方面，数学史学家致力于挖掘古代数学家事迹和数学理论方法的特征及其产生的数学思想和理论方法对于哲学和文化情景的依赖。可见，数学教育与数学史研究之间的目标和方法都不完全相同，认为在数学教学中，引导学生进入数学发展的深邃历史情景和过程中，来感知现在学习的数学内容，这一教学设计理念在付诸实施时似乎感觉有点困难，甚至浪费时间。

（二）从实践上对数学史融入数学教学的质疑

针对数学史融入数学教学，Tzanakis和Arcavi[8]等研究学者认为，现阶段的数学教学实际上还不完全满足引入数学史的条件。主要表现在以下四点：第一，缺乏时间。数学教师都感受到在开展数学教学过程中，抽取一定的時间（即使占用全部教学时间比例很低）来完成教学活动，以达到良好的教学效果的目的，还存在一定的困难。第二，缺乏资源。在数学教学中，数学教师并没有完整、丰富和系统的数学史书籍及其参考资料给予使用。第三，缺乏学习和培训。没有长期、中期或者短期安排、计划和规划，对数学教师进行充分的系统性和科学性的数学史知识体系学习和培训及其对教学经验的交流和学术研讨。第四，缺乏良好的教学现实条件，包括缺乏与数学氛围相适应的教学环境，全方位呈现数学教学素材和各个环节要素的教学设施，客观科学的数学教学评价体系等。

除此之外，对不同层次数学课程（含中小学、大学、高职和民族预科等）进行教学，应根据各自规定的课程教学大纲、课程教学目标和课程规划等，要求必须在规定的教学时间内和相应的教学条件下完成相应的教学任务。从实际的教学实践和教学经验中，还可以认识到，教师要完成数学课程所规定的教学任务，不能一味地填鸭式逐一讲解全部的知识点。客观上，应用数学各种史料，可以对数学中的概念、定义、相关理论和方法等，能够提供一定的历史背景、文化环境等，对数学教学有一定的促进作用，具有极高的教育价值。数学从来不是某个人、某个文明、某个国家和地区的专利，不同文化都对数学的发展产生过影响，数学在不同时空的历史演进，也是数学学习的目标[9]。这与数学课程目标的实现并无根本上的冲突，两种应该是相得益彰、互相促进的。

但是在数学教学中，不能忽略这样一类问题：数学史的内容与数学课程的教学内容在教学时间上如何分配，数学史融入数学教学的模式怎样处理，等等，这在实际开展数学教学活动时将是难以选择的。首先，数学史能够发挥积极教育价值，占用比较多的教学时间是不可取的。其次，同样在数学教学中，完全不使用数学史或者象征性粗糙式使用数学史，仅仅在数学教学中对数学史料的使用流于形式，会导致数学史对教学的积极教育价值得不到充分发挥。

在客观上，数学史与数学教育建立和制定的理论体系、实施方案及其所依据的理念、形式和方式，都存在一定的差异性。将数学史与数学教学之间进行相互融合并不容易，可能存在一定的距离。数学史融入数学教学的运用还存在一些因素的制约，主要包含教师对数学史内涵理解上的局限性，教师可支配的数学史素材不全面、不系统，教师在数学教学中使用数学史料会受到学生实际水平和数学教学现实条件限制，等等。诸如此类因素，很大程度上限制了教师在数学教学中高水平的发挥。余庆纯和汪晓勤采用德尔菲法、文本分析法开展质性研究，对2012—2018年20个高中HPM课例分析发现，在HPM视角下的数学教学中，数学史的教育价值功能仍体现不足[10]，探究其原因，存在上述因素制约了数学史融入数学教学中教育价值的发挥。

三、双循环诠释学模式

1994年，德国教授H.N. Jahnke在第18届PME大会报告中指出：数学是一种文化，回归源头能使我们获得对思想过程的重要认识，更加清晰地理解现在问题[11]。Jahnk的报告内容主要阐述了下列观念：（1）数学史融入数学教学的重要性不仅仅是为了激发学习动机和学习兴趣等外在目标，而应该是把数学发展过程中同时期和不同时期数学文化联系起来，使数学史成为支持数学教育中教与学的必要组成部分。（2）同时期的数学史包含数学课程教学对话和教学活动的自然情景，对相应的数学概念、定义等能够产生一定的共鸣， 不同时期的数学史可以展现数学的发展历程，能够感受到由简单到复杂、由直观到抽象及其数学来源于实践并最终应用于实践等变化方程。（3）在数学教学中，通过对数学假设、理论、特征的理解、诠释和融入，让学生在数学学习中，在一定的社会文化背景下掌握数学知识的建构意义、思维模式及其发生发展形式，不仅实现了数学认知的发展，还实现了更重要的元数学认识的发展[2]。

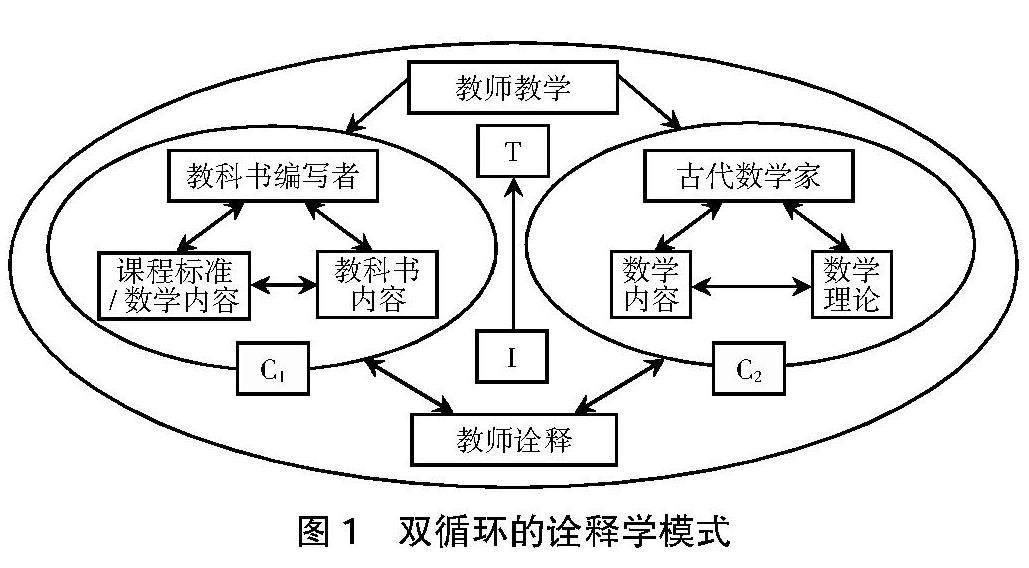
基于这种对数学教育的认知观念，形成了数学史融入数学教学的一种模式，称之为双循环诠释学模式[12]，如图1所示。

■

图1 双循环的诠释学模式

这种诠释学模式不仅要考虑数学史，还需要考虑其他数学教学要素，比如教学内容、教科书、课程标准、教学理论和教学方式等。首先，在数学教学准备开展之前，可以反复向自己提出类似这样的问题：有没有必要引入数学史？ 数学史和教学内容的内在联系在哪里？ 数学史对数学学习的贡献和价值是什么？ 等等。对于这类问题，数学教师在实施数学教学活动之前的准备阶段需作出诠释，即教师对数学史及其与数学教学的联系的理解和思考。其次，教师带着自己的诠释必须经过两个循环过程，即C1循环过程和C2循环过程，寻找C1循环过程与C2循环过程之间的联系，着眼于评估数学史在此教学过程中能否发挥积极作用、如何发挥作用及其作用发挥的程度怎么样，来决定是否有必要将数学史融入此数学教学过程。若有必要，需要制定出数学史与具体的教学内容结合的方式及其数学史呈现的形式，并对教学效果进行预期的评估。

C1循环过程：主要包含教师对教材编写者的意图、课程标准、教学目标和教科书知识等进行一定程度的理解和分析，再结合课程目标、教学任务和教学环境等，教师反复思考此教学内容是否有必要融入数学史来开展数学教学过程。

C2循环过程：主要包含教师对古代数学家事迹及其历史背景、相对应的数学理论、数学思想和数学内容等进行一定程度的认识和理解，反复思考和挖掘与相应的数学教学内容密切相关的具体数学史内容，比如数学史实、数学趣事及其历史上数学理论和方法的产生过程等，可以融入数学教学中。

虽然教师结合现有的数学理论和数学史知识体系，可以在一定程度上独立去诠释C1循环过程和C2循环过程，形成一定的教学方式。但事实上，在数学教学展开之前必须思考一个关键性问题：在C1循环过程和C2循环过程之间，如何去探索一个恰当的结合程度？

四、多向循环诠释学模式

（一）诠释学模式的探索

利用双循环诠释学模式，在开展数学教学时，经过C1循环和C2循环过程后，教师只能根据教材的编写、课程标准、教学内容和教学目标，对数学思想和方法产生和发展的历史过程及其特征等进行诠释，进而挖掘可以在教学中使用的数學史知识内容，寻找数学史与教学内容恰当的结合角度。但是，并没有考虑学生的实际情况和现有的知识水平及其数学教学现实条件（数学氛围、教学环境、教学设施、教学评价体系等）等与数学教学相关的因素。

数学教学活动应该是以学生为中心展开的，在探索数学史融入数学教学模式时，更应该把有利于教学和学生学习放在衡量教学优劣的主体地位，故应对学生的实际情况、知识水平和结构引起重视。除此之外，还应该考察数学教学现实条件，包括数学氛围、教学环境、教学设施和教学评价体系等，和其他有益于数学教学中使用数学史的方式和途径。

（二）多向循环诠释学模式的实践

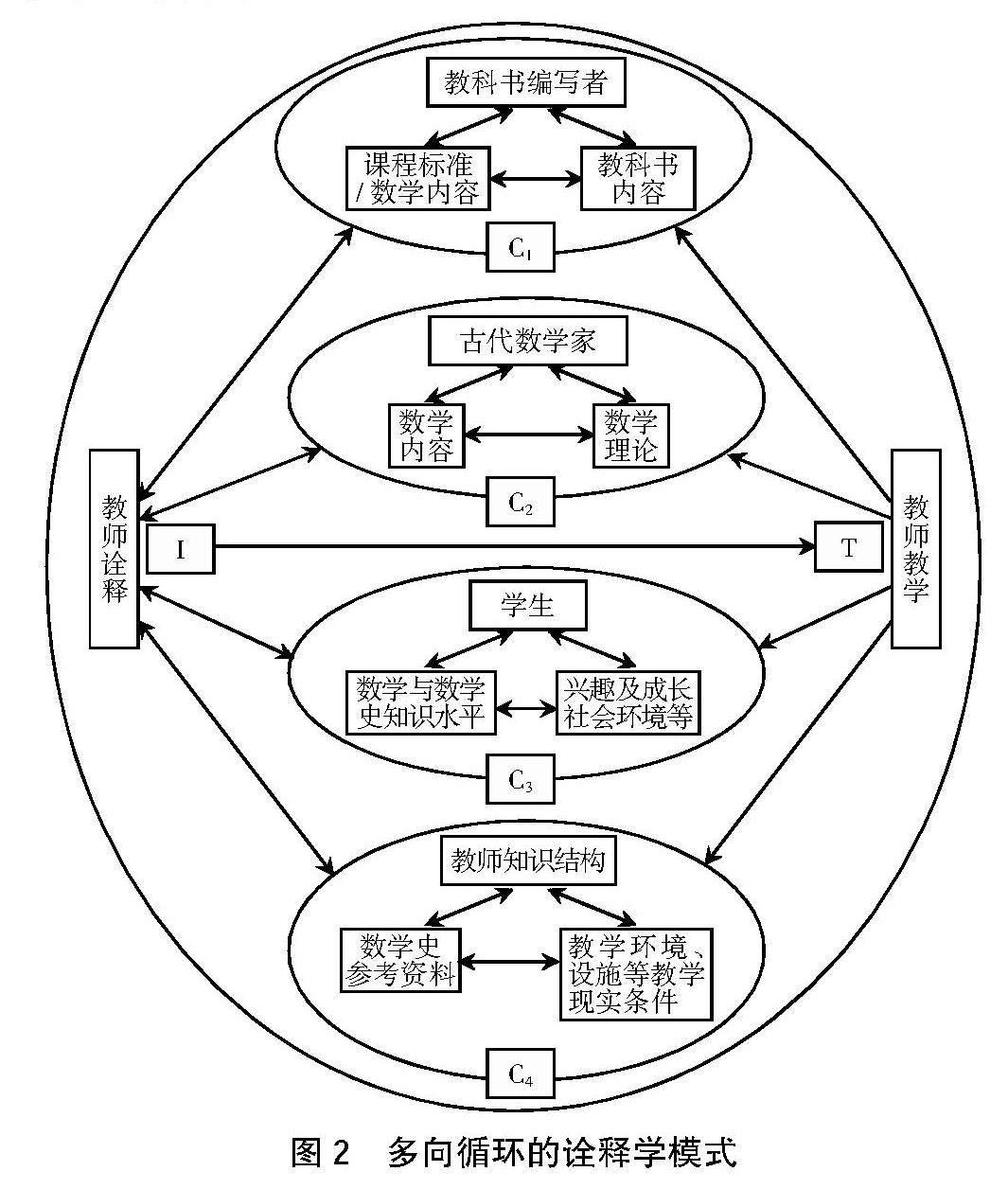
为了数学史融入数学教学能够取得较好的教学效果，有必要对双循环诠释学模式适当地进行改进，使之更好地在实践上指导数学教学。现在针对数学史融入数学教学的模式，提出一种新的多向循环诠释学模式，如图2所示。

■

图2 多向循环的诠释学模式

多向循环诠释学模式描述如下：

1.此多向循环诠释学模式并不局限于满足双循环诠释学模式中C1和C2两个循环过程，即针对数学教科书和数学史两方面，增加了关于学生实际水平和教学现实条件两个循环。在此改进的诠释学模式中，只要是将数学史融入数学教学，有利于提高教学和学习效率的方式和途径，都可以加入循环中去，这样就可以把影响数学教学效果的若干要素尽量充分地予以考虑，综合衡量，探索数学史与数学教学内容的最佳结合角度，这样的结合角度更加符合客观实际，形成恰当和相适应的方式，使数学史融入数学教学的方式更符合学生的认知水平，凸显教师的教学效果，充分发挥数学史的教育价值。

2.多向循环诠释学模式强调开展数学教学之前的准备阶段，必须考虑学生的认知水平和知识结构，也要考查学生目前所掌握的有关数学史知识水平，评估对新知识及相应的数学史是否感兴趣或感兴趣的程度如何及接受数学史的方式，和学生可能面临的问题等，并尝试结合目前的学习特点对效果作一个预期的评估，并及时进行修正。

上述问题如何去做才能更好地解决？ 可以在教学活动开展之前，进行一个与教学活动相关的调查问卷，了解学生目前的状况及对新知识的前期反应情况。除了调查问卷，教师可以通过对不同层次的学生进行访谈等方式了解学生目前的实际情况。

3.多向循环诠释学模式也重视对数学现实条件这一因素的思考。客觀上，数学现实条件能够对数学教学活动的开展产生不可估量的影响，同时为学生的学习提供了一个先决条件，营造了良好的学习氛围，故在某种程度上可以直接影响教师的教学效果和学生的学习效果。这里考虑的教学现实条件包含数学氛围、教学环境、教学设施、教学评价体系等， 在客观上是不可否认的。这些教学现实条件现有的状况，对数学史融入数学教学产生的教学效果将会有不同程度的影响，必须认识到现有教学现实条件的不完善，对数学史积极教育价值的发挥将会产生一定程度限制。

五、结束语

多向循环诠释学模式主要从教科书、数学史、学生实际水平和教学现实条件四个方面予以综合考虑，并进行诠释，对数学史融入数学教学的有效方式及途径进行充分的思考和探索，这样可以找到更恰当的结合角度，使之更符合学生和教学现实条件等实际要求，将数学史融入数学教学，以发挥数学史更大的教育价值。与双循环诠释学模式相比较，多向循环诠释学模式考虑的影响数学教学的要素比较全面，对数学教学活动的开展具有一定的指导价值。

参考文献：

［1］刘思璐，韩嘉业，姜浩哲.第八届全国数学史与数学教育学术研讨会纪要［J］．数学教育学报，2020，29（1）：93-97.

［2］朱凤琴，徐伯华．数学史融入数学教学模式的国际研究与启示［J］．数学教育学报，2010，19（3）：22-25．

［3］Iris G.， Klaske B..“Ahistorical Angle”，a Survey of Recent Literature on the Use And Value of History in Geometrical E Education［J］. Educational Studies in Math-ematics，2001（47）：223-258.

［4］张晓贵，张雪．国外数学教学中引入数学史的研究综述［J］．数学教育学报，2013，22（4）：43-46．

［5］Radford L.. On Psychology， Historical Epistemology， and the Teaching of Mathematics：Towards a Socio-cultural History of Mathematics［J］. For the Learning of Mathematics， 1997，17（1）：26-33.

［6］Unguru S.. Words， Diagrams， and Symbols： Greek and Modern Mathematics or，“On the Need to Rewrite the History of Greek Mathematics” Revisited［J］. St. Johns Review， 2004（1）： 91-114.

［7］Fried M. N.. Can Mathematics Education and History of Mathematics Coexist［J］. Science & Education，2001 （10）： 391-408.

［8］Tzanakis C.， Arcavi A.. Integrating History of Mathe-matics in the Classroom： an Analytic Survey［A］. In： Fauvel J， van Maanen J. History in Mathematics Education［C］.The ICMI Study Dordrecht： Kluwer Acad-emic Pub-lishers，2000.

［9］Jankvist T. U..  A Categorization of the “Whys” and“Hows” of Using History in Mathematics Education［J］. Educational Studies in Mathematics，2009（71）：235-261.

［10］余庆纯，汪晓勤.基于数学史的数学文化内涵实证研究［J］．数学教育学报，2020，29（3）：68-74．

［11］Jahnke H. N.. The Historical Dimension of Mathe-matical Understanding： Objectifying the Subjective ［A］. In： J P Ponte， J F Matos. Proceedings of the 18th Inter-national Conference for the Psychology of Mathe-matics Education［C］.Lisbon： University of Lisbon， 1994.

［12］张维忠，汪晓勤．文化传统与数学教育现代化［M］．北京：北京大学出版社，2006．

◎编辑 尹 军