泰勒公式与高考试题
⦿ 湖北省荆州中学 谢 俊
泰勒(Taylor)以微积分中将函数展开成无穷级数的定理而著称于世.泰勒公式把初等函数与超越函数以逼近形式紧密地联系了起来,泰勒公式扮演了非常重要的角色,泰勒公式即有高考导数命题中最常见的高等数学背景,又有以其背景而衍生出来的一些精彩结论.这些结论备受高考命题者的青睐,本文中试图就历年的高考试题来探究其深厚的渊源,从而展示泰勒公式阿娜多姿的风采.
1 高数知识
1.1 泰勒公式
若函数f(x)在点x0处存在n阶导数,则有

①
上面①式也称为麦克劳林(Maclanrin)公式.
1.2 常见的泰勒公式

截取片段,就构成了高考中常见的不等式:
由泰勒公式演绎出来的不等式是高考的热点,通过对其变形、赋值、替换等,又可以得出很多精彩的结论.我们对这些结论追本溯源,掌握其基本规律,就可以从容面对,快速找到解题思路、方法.
2 高考试题
2.1 泰勒公式与大小比较
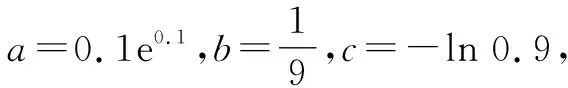
A.a C.c 解:由泰勒公式,有 显然c 例2(2021年八省新高考适应考试题)已知f(x)=ex-sinx-cosx,g(x)=ex+sinx+cosx. (2)若g(x)≥2+ax,求a. 解:(1)证明略. (2)(必要性探路)由泰勒公式,有 ② ③ ④ 由②+③+④,得 上式中,sinx,cosx中的负项全部被ex中的正项抵消,于是得到g(x)=ex+sinx+cosx≥2+2x成立,所以,背景出来了,a=2. (充分性证明)在(1)中,令 F(x)=g(x)-2-ax=ex+sinx+cosx-2-ax. 故当a=2时,F(x)≥0. 综上所述,可知a=2. 例3(2014年新课标Ⅱ卷)已知f(x)=ex-e-x-2x. (1)设g(x)=f(2x)-4bf(x),当x>0时,g(x)>0,求b的最大值; 解:(1)由题意知g(x)=f(2x)-4bf(x)=(e2x-e-2x-4x)-4b(ex-e-x-2x). 所以b≤2.故b的最大值为2. 例4(2018年新课标Ⅲ卷)已知函数f(x)=(2+x+ax2)ln(1+x)-2x,若x=0是f(x)的极大值点,求a的值. 解:(2)由泰勒公式,有 例5(2020年高考全国Ⅰ卷)已知函数f(x)=aex-1-lnx+lna,若f(x)≥1,求a的取值范围. 解:当0 当a>1时,有 f(x)=aex-1-lnx+lna>ex-1-lnx≥1. 由泰勒公式,有 于是有ex≥1+x,把x换成x-1,得ex-1≥x. 于是有ln(1+x)≤x,把x换成x-1,得lnx≤x-1,即-lnx≥1-x. 所以,ex-1-lnx≥1,此式即当a=1时的情形. 综上,a的取值范围为[1,+∞). 例6(2017年高考浙江卷)已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1),n∈N*.证明:当n∈N*, (1)0 证明:第(1)问略. (3)由泰勒公式,有ln(1+x)≤x(x>0). 泰勒公式在高考试题中的美妙身姿何止这些,限于篇幅,在此就不再一一撰述.尽管高考试题的设计有来源于泰勒公式,但命题者提供的方法,最终还是要用中学所学的导数知识来解决,但是如果利用泰勒公式来思考,则解题思维会更加流畅,更容易接近问题的本质[1]. 泰勒公式是高等数学的知识,直接应用恐有失分,但如果知道常见函数的泰勒公式,我们就很容易发现试题的背景,应用初等数学方法解决即可[2].学习高中数学适当掌握一点高等数学知识,对于学生来说不仅仅是一举多得的好事,更可以直达“会当临绝顶,一览众山小”的解题仙境!
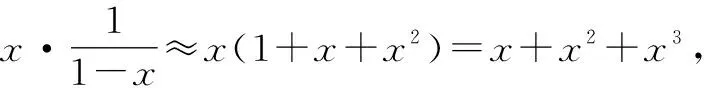
2.2 泰勒公式与探路求值


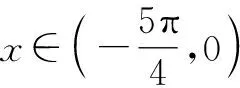

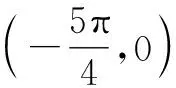

2.3 泰勒公式与近似估值



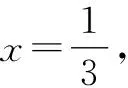
2.4 泰勒公式与极值界定


2.5 泰勒公式与放缩变形
2.6 泰勒公式与数列不等式